| ρ′= | Q
|
|
(9.24) |
|
(9.25) |
|
(9.26) |
|
(9.27) |
|
(9.28) |
 Fμνは、いわばAμの4次元rotである。3次元のrotでは、「ベクト
ルのrotはベクトル」であったが、実はこれが成立するのは3次元でだけである。なぜなら、その定義上、rotは「微小な面を考えて、その回りをぐるっと
回る」という操作に対応している。3次元では、面は3つある(xy平面、yz平面、zx平面)。しかし、2次元ではxy平面一つしかないし、4次元では
xy,yz,zxの他にxt,yt,ztを合わせて合計6つある。重複をゆるさず二つの方向を決めれば面が決まるので、一般にn次元では[n(n−1)
/2]個の面がある。
3次元のrotのdivを取ると0になることは、空間内に立方体を描くことで示すことができた。4次元のrotであるところのFμνで
も、4つの座標軸(ct,x,y,z)のうちから3つ選んで立方体を作り、その立方体の各面を回るようなrotを考えることで同様の式を作ることができ
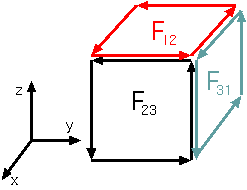
る。例えば上の図は(x,y,z)の3つの軸で立方体を作った場合である。天井と床から∂z F12=∂z
Bzが出る(天井と床では逆符号なので、(天井)−(床)という計算がされ、微分になるのである。同様に、左と右から∂y
F31=∂y Byが、正面と裏から∂x F23=∂x
Bxが出る。全部足すとdiv→B=0が出る。
Fμνは、いわばAμの4次元rotである。3次元のrotでは、「ベクト
ルのrotはベクトル」であったが、実はこれが成立するのは3次元でだけである。なぜなら、その定義上、rotは「微小な面を考えて、その回りをぐるっと
回る」という操作に対応している。3次元では、面は3つある(xy平面、yz平面、zx平面)。しかし、2次元ではxy平面一つしかないし、4次元では
xy,yz,zxの他にxt,yt,ztを合わせて合計6つある。重複をゆるさず二つの方向を決めれば面が決まるので、一般にn次元では[n(n−1)
/2]個の面がある。
3次元のrotのdivを取ると0になることは、空間内に立方体を描くことで示すことができた。4次元のrotであるところのFμνで
も、4つの座標軸(ct,x,y,z)のうちから3つ選んで立方体を作り、その立方体の各面を回るようなrotを考えることで同様の式を作ることができ
る。例えば上の図は(x,y,z)の3つの軸で立方体を作った場合である。天井と床から∂z F12=∂z
Bzが出る(天井と床では逆符号なので、(天井)−(床)という計算がされ、微分になるのである。同様に、左と右から∂y
F31=∂y Byが、正面と裏から∂x F23=∂x
Bxが出る。全部足すとdiv→B=0が出る。
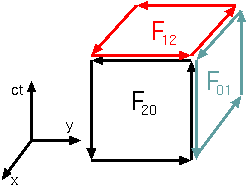 (ct,x,y)の3つの軸を使って作った図が左のもので、この場合は天井と床から∂0 F12=1/c∂t
Bx、左と右から∂y F01=−1/c∂y
Ex、正面と裏から∂x F20=1/c∂x
Eyが出る。全部足して分母のcを払うと、
(ct,x,y)の3つの軸を使って作った図が左のもので、この場合は天井と床から∂0 F12=1/c∂t
Bx、左と右から∂y F01=−1/c∂y
Ex、正面と裏から∂x F20=1/c∂x
Eyが出る。全部足して分母のcを払うと、
|
(9.29) |
|
(9.30) |
|
(9.31) |
|
(9.32) |
|
(9.33) |
|
(9.34) |
|
(9.35) |
|
(9.36) |
|
(9.37) |
|
(9.38) |
|
(9.39) |
|
(9.40) |
|
(9.41) |
|
(9.42) |
|
(9.43) |
|
(9.44) |
|
(9.45) |
|
(9.46) |
|
(9.47) |
|
(9.48) |
|
(9.49) |
|
(9.50) |
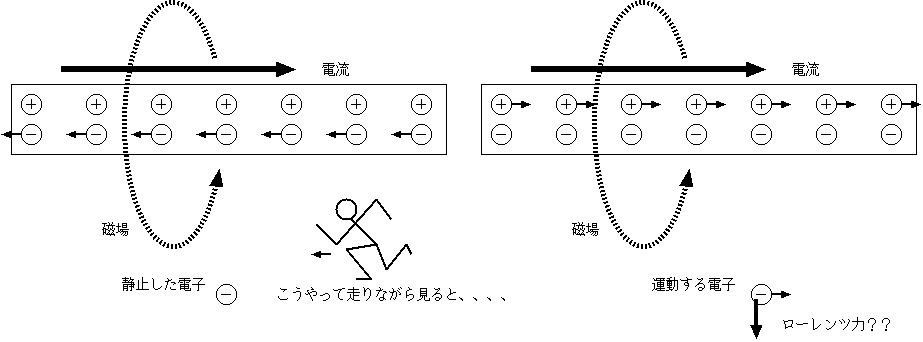
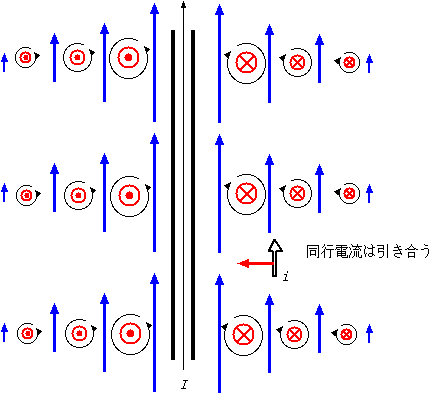
電流が流れている導線から少し離れたところに静止した電子がいる。導線には流れている自由電子(−電荷)がいるが、 静止している金属イオン(+電荷)もいて、全体として電荷は中和している。ゆえに導線のまわりに電場はない。電流があるから磁場はあるが、磁場は止まって いる電子に力を及ぼすことはない。よってこの電子は力を受けない。 ここで、流れている電子と同じ速度で移動しながらこの現象を見たとしよう。電子は止まってしまうが、金属イオンは逆に動き出すので、やはり電流は流れて いる。故に磁場はやはり発生している。今度は外においてある電子は動いている。磁場中を動く電子は力を受けるので、この立場で考えると電子には力が働く。 さて、はたして電子に力は発生するのか、しないのか??電線の中の電子の動く速度はけっこうゆっくり(歩く速度より遅いぐらい)なので、この実験は実際にやることができるが、もちろん、電子は動かない。見る人 の立場によって結果が変わるはずはない。 相対論を知っていると、この謎には下の図のような答を出すことができる。すでに電磁場のローレンツ変換を求めておいたので、それを見てもらうとわかると思 うが、導線に対して動く人から見ると、導線に対して止まっている人には見えない電場が見えるのである。
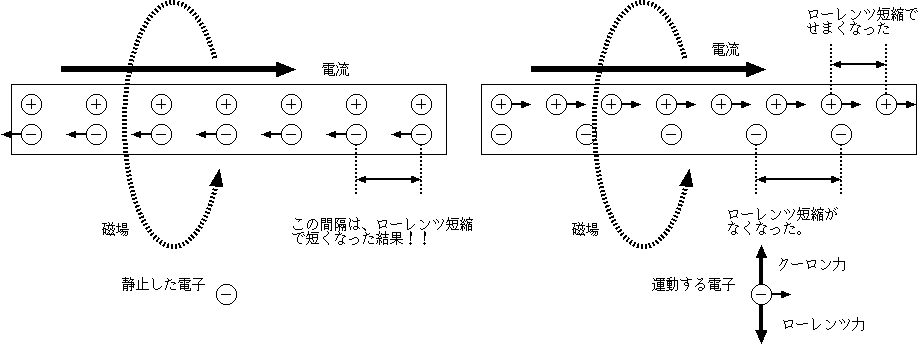 この電場はもちろん、理由もなく発生するのではない。電場が発生する原因は、導線の中を考えるとわかる。最初導線内には等しい電荷があって電場がキャン
セルしている、と言ったが、相対論によれば動いている物体はローレンツ短縮で長さが縮むはず。一群の電荷が動いたとすると、運動方向に圧縮されて電荷密度
が上がることになる。ということは、今導線内にある電子の流れは「すでにローレンツ短縮した結果」として+電荷とキャンセルしている。これを動きながら見
ると、今度は+電荷がローレンツ短縮により圧縮され、電子の方は逆に圧縮される原因がなくなり、いわば「圧縮が解除される」ことになるのである。結果とし
て、運動しながら見ると導線は+に帯電していることになる。この+に帯電した導線は電子を内側にひっぱり、磁場によるローレンツ力を打ち消す。
この問題が教えてくれる教訓は「相対論なんてのは宇宙の話や素粒子の話をする時にしか出てこない、特殊な世界の話」と思いこんではいけないということで
ある。量子力学がミクロな世界にとどまらないように、相対論も普段見る物理現象にも効いているのある。相対論の助けなしには、電磁気現象を完全に理解する
ことはできない。
この電場はもちろん、理由もなく発生するのではない。電場が発生する原因は、導線の中を考えるとわかる。最初導線内には等しい電荷があって電場がキャン
セルしている、と言ったが、相対論によれば動いている物体はローレンツ短縮で長さが縮むはず。一群の電荷が動いたとすると、運動方向に圧縮されて電荷密度
が上がることになる。ということは、今導線内にある電子の流れは「すでにローレンツ短縮した結果」として+電荷とキャンセルしている。これを動きながら見
ると、今度は+電荷がローレンツ短縮により圧縮され、電子の方は逆に圧縮される原因がなくなり、いわば「圧縮が解除される」ことになるのである。結果とし
て、運動しながら見ると導線は+に帯電していることになる。この+に帯電した導線は電子を内側にひっぱり、磁場によるローレンツ力を打ち消す。
この問題が教えてくれる教訓は「相対論なんてのは宇宙の話や素粒子の話をする時にしか出てこない、特殊な世界の話」と思いこんではいけないということで
ある。量子力学がミクロな世界にとどまらないように、相対論も普段見る物理現象にも効いているのある。相対論の助けなしには、電磁気現象を完全に理解する
ことはできない。