実例:流行の方程式
「ある流行(服でも靴でもいい)がどのように時間的に流行していくかを方程式で示す」を微分方程式として考えてみよう。全人口の${y}$倍がすでにその流行に乗っている(つまり服を着るなり靴を履くなりしている)としよう。変数${y}$の意味は、${y}=0$なら「誰も着てない」、${y}=1$なら「全員が着ている」という状態である実際には女性用の服なら男性が着ることはあまりないから、その場合は${y}$を全人口ではなく女性人口の割合にする、などの修正は必要である。。単純に考えると「回りの人が着ていたら自分も着たくなるだろう」と考えると、
\begin{equation} {{\mathrm d}y\over \mathrm dt}= k{y} \end{equation}という「回りにいる人が着ている率に比例して着る人が増えていく」という式にしたくなる。ところがこれだと${y}$はどんどん上昇して1を超えてしまう(全人口より着ている人の方が多い??)。なぜこうなったかというと、「すでに着ている人は影響を受けない」ということを考えてなかったからである。つまり、「今から着よう」と決断することができるのは、まだ着ていない人(全体の$1-{y}$倍の人)だけである。そう考えると微分方程式は
\begin{equation} {{\mathrm d}y\over \mathrm dt}= k{y}(1-{y})\label{ryukouone} \end{equation}となる。これを解くには、
\begin{equation} {{\mathrm d}y\over {y}(1-{y})}= k\mathrm dt \label{ryukoutwo} \end{equation}のように変数分離する(ここで、${y}(1-{y})\neq0$を仮定したことに注意)。この積分は
\begin{equation} {1\over {y}(1-{y})} = {1\overbrace{-{y}+{y}}^0\over {y}(1-{y})} ={1\over {y}}+{1\over 1-{y}} \end{equation}と分数を書き直すことで
\begin{equation} \begin{array}{rl} {{\mathrm d}y\over {y}}+{{\mathrm d}y\over 1-{y}} =&k\mathrm dt \\ \log |{y}|-\log|1-{y}|=&k {t}+C \\ \end{array} \end{equation}と積分できる($C$は積分定数)。この段階では$0\leq {y}\leq 1$という状況で考えているので、本来は絶対値を取るという操作は不要である前にも書いたが、$C$が複素数であってよければ、そもそもこの絶対値は必要ない。が、後で使うので今はつけてある。
これを整理すると
\begin{equation} \begin{array}{rl} \log \left|{{y}\over 1-{y}}\right|=&k {t}+C \\ {{y}\over 1-{y}}=&\pm\mathrm e^{k {t}+C} ~~(絶対値外しで\pm が付く) \\[3mm] {y} =&\pm(1-{y})\mathrm e^{k {t}+C} \\[3mm] {y}\left( 1\pm\mathrm e^{k {t}+C} \right) =&\pm\mathrm e^{k {t}+C} \\ {y} =& {\pm\mathrm e^{k {t}+C}\over 1\pm\mathrm e^{k {t}+C} } ={1\over 1\pm\mathrm e^{-k {t}-C} } \end{array} \end{equation}となる。この結果をグラフにすると次のようになる(下のスライダで$k$と$C$を調節できる)。
k=
C=
途中で複号$\pm$をつけたが、これは${{y}\over 1-{y}}$が正のとき$+$、負のとき$-$である。よって本来解こうとしていた問題においては$+$をとっておけばよい(グラフもそうしている)。
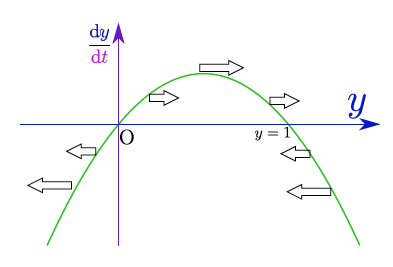
ここでは、${y}=0$から${y}=1$までの範囲だけを考えた(もともとの${y}$という変数の意味からするとそれで十分である)。少し話を一般的にすることにして、${{\mathrm d}y\over \mathrm dt}= k{y}(1-{y})$という微分方程式の解が一般的にどのような形を取るかを考察しておこう。
傾き${{\mathrm d}y\over \mathrm dt}$は${y}=0$と${y}=1$で0となり、その間の範囲で正、それ以外の場所で負である。よって時間経過した時の変化を考えると、$0<{y}<1$では増加し、それ以外では減少する。結果として${y}$の値は${y}=1$へと集まっていく(そして、${y}$からは離れていく)という傾向を示す。
ここでもう一つ注意しておこう。今求まった${y}={1\over 1-\mathrm e^{\pm k {t}-C}}$という解には実は厳密には「抜け」がある。${y}=0$と${y}=1$(定数で、このままずっと変化しない)というのも、もともとの微分方程式の解であるが、それは今求めた解の複号$\pm$と積分定数$C$の値をどう決めても出てこない。つまり、今求めた解は非常に微妙なところで「一般解」になり損なっている。
${y}={1\over 1-\mathrm e^{\pm k {t}-C}}$で$C=\pm\infty$とすれば${y}=1$や${y}=0$になる---ように見えるかもしれないが、これは正しい計算ではない。というのは、そもそも$\infty$というのは代入できる数ではない。「$C$をどんどん大きくしていく極限」として定義される量である。$C$をどんどん大きくすると分母の$\mathrm e^{\pm k {t}-C}$が0に近づくかと思われるが、定数である$C$がいくら大きくとも、前にある$\pm k{t}$の項が$C$を打ち消すほどに小さくなることができる(この項は変数${t}$を含んでいることに注意)から、$\mathrm e^{\pm k {t}-C}=0$とは言えないのである(逆に$C$がどんどん小さくなる場合も同様)。よって${y}={1\over 1-\mathrm e^{\pm k {t}-C}}$は${y}=0$と${y}=1$を含まない。
「抜け」が生じてしまった理由は明白で、その原因は式変形の途中において両辺を${y}(1-{y})$で割ったところにある。割算する時には、割る数が「0でないかどうか」を確認しなくてはいけない。つまり${y}(1-{y})$で割ったことにより、そこから後の式は${y}(1-{y})\neq0$の場合に限る話になっているのである。よって、${y}(1-{y})=0$の場合を別に考慮しなくてはいけない(もちろん、それが解になってないならその可能性を捨てればよい)。
この場合、${y}=0$と${y}=1$と一定になる場合は右辺も左辺(${{\mathrm d}y\over \mathrm d x}$)も0になるから、これも解となる。この二つは今求めた解${y}={1\over 1-\mathrm e^{\pm k {t}-C}}$に含まれない解となっていた。このような解を「特異解」と呼ぶこともある。
今の場合の(文字通りの)一般解は、
\begin{equation} {y}={1\over 1-\mathrm e^{\pm k {t}-C}}(Cは任意定数)~~または~~{y}=0~~または~~{y}=1 \end{equation}ということになる。
↑ちなみに私はこれを聞いた時は「CMなどの広告」という答を予想していた。
連立の場合はまだやってないので、ここでは式を立てるだけにする。
↑この問題を今日の小テストにしました。
ヒントとして、口コミの場合の$ky(1-y)$のうち$y$の微分は「周りが持っている割合」だけど、CMで見る場合は周りが持っているかどうかは無関係だとして、この$y$がなくなると考えればよい。一方、「すでに買ってしまった人は買わない」というのは本当だろうから、$(1-y)$はこの場合でもあるだろう、というところまでは説明しました(ヒント出しすぎたかもしれない)。
まず微分方程式は、
${\mathrm dy\over\mathrm dt}=M(1-y)$
となる。 つまりまだ買ってない人の割合である1-yに比例して増えるとして計算する。
これを変数分離して積分すると、
${\mathrm dy\over 1-y}= M\mathrm dt$
$-\log(1-y)=Mt +C$
整理して、
$y=1-\mathrm e^{-Mt-C}$
である。これは$y=1$にどんどん近づいていく関数。