積分可能条件
偏微分も常微分同様、二階微分、三階微分があり、その記号も
\begin{equation} \left( {\partial\over \partial x} \left({\partial f({x},{y})\over \partial x}\right)_{\!\!{y}} \right)_{\!\!{y}} =\left( {\partial^2 f({x},{y})\over \partial x^2}\right)_{\!\!{y}} ,~~ \left( {\partial\over \partial y} \left({\partial f({x},{y})\over \partial y}\right)_{\!\!{x}} \right)_{\!\!{x}} =\left( {\partial^2 f({x},{y})\over \partial y^2}\right)_{\!\!{x}} \end{equation}のように常微分の場合に似た書き方にする。偏微分の場合は、
\begin{equation} \left( {\partial\over \partial x} \left({\partial f({x},{y})\over \partial y}\right)_{\!\!{x}} \right)_{\!\!{y}}={\partial^2 f({x},{y})\over \partial x \partial y} \end{equation}のように「最初に${y}$で微分、次に${x}$で微分」のような計算も出てくる（上の式の右辺は固定する変数を省略する書き方を使った）。分母の書き方が常微分と決定的に違うところなので注意しようここで、${\partial^2 f({x},{y})\over \partial x\partial y}$と${\partial ^2 f({x},{y})\over \partial y\partial x}$は違うのか？---という疑問を持った人もいるだろう。その答はすぐ後で。。
偏微分の交換可能性
\begin{equation}\begin{array}{c} {\partial \over \partial x}\left(\left( {\partial f({x},{y})\over \partial y}\right)_{\!\!{x}} \right)_{\!\!{y}} = {\partial \over \partial y}\left(\left( {\partial f({x},{y})\over \partial x}\right)_{\!\!{y}} \right)_{\!\!{x}} \\[8mm] または\\[4mm] {\partial^2 f({x},{y})\over \partial x \partial y} ={\partial^2 f({x},{y})\over \partial y \partial x}~~~\leftarrow {\scriptstyle 一定にする変数を省略した書き方} \end{array}\label{henbibunkoukan} \end{equation}上の式、すなわち偏微分が交換可能であることを確認する。これを${y}$で偏微分するということは
\begin{equation} \begin{array}{rl} \left({\partial \over \partial y}\left( {\partial f({x},{y})\over \partial x}\right)_{\!\!{y}} \right)_{\!\!{x}} =& \lim_{{\Delta y}\to0} {\left( {\partial f({x},{y}+{\Delta y})\over \partial x}\right)_{\!\!{y}} -\left( {\partial f({x},{y})\over \partial x}\right)_{\!\!{y}} \over {\Delta y}} \end{array}\end{equation}という計算だが、この式の分子にさらに偏微分の定義を代入することで
\begin{equation} \begin{array}{rl} =& \lim_{{\Delta x}\to0\atop{\Delta y}\to0} {{ f({x}+{\Delta x},{y}+{\Delta y}) -f({x},{y}+{\Delta y})\over {\Delta x}} -{f({x}+{\Delta x},{y}) -f({x},{y})\over {\Delta x}} \over {\Delta y}}\\[5mm] =& \lim_{{\Delta x}\to0\atop{\Delta y}\to0} { f({x}+{\Delta x},{y}+{\Delta y}) -f({x},{y}+{\Delta y}) -f({x}+{\Delta x},{y}) +f({x},{y}) \over {\Delta x}{\Delta y}} \end{array}\label{DxDyf} \end{equation}を得る。次に${x}$で偏微分すると、結果は${x}$と${y}$の微分の順番を変えただけなので、
\begin{equation} \left( {\partial \over \partial x}\left( {\partial f({x},{y})\over \partial y}\right)_{\!\!{x}}\right)_{\!\!{y}} =\lim_{{\Delta x}\to0\atop{\Delta y}\to0} { f({x}+{\Delta x},{y}+{\Delta y}) -f({x}+{\Delta x},{y}) -f({x},{y}+{\Delta y}) +f({x},{y}) \over {\Delta x}{\Delta y}}\label{DyDxf} \end{equation}を得る。注意深く見れば、（引き算の順番が入れ替わっているが）同じ式なのがわかる。
図で表現しておこう。省略形で${\partial\over \partial y}\left({\partial f\over \partial x}\right)$になる微分を図で表現したのが次の図である。
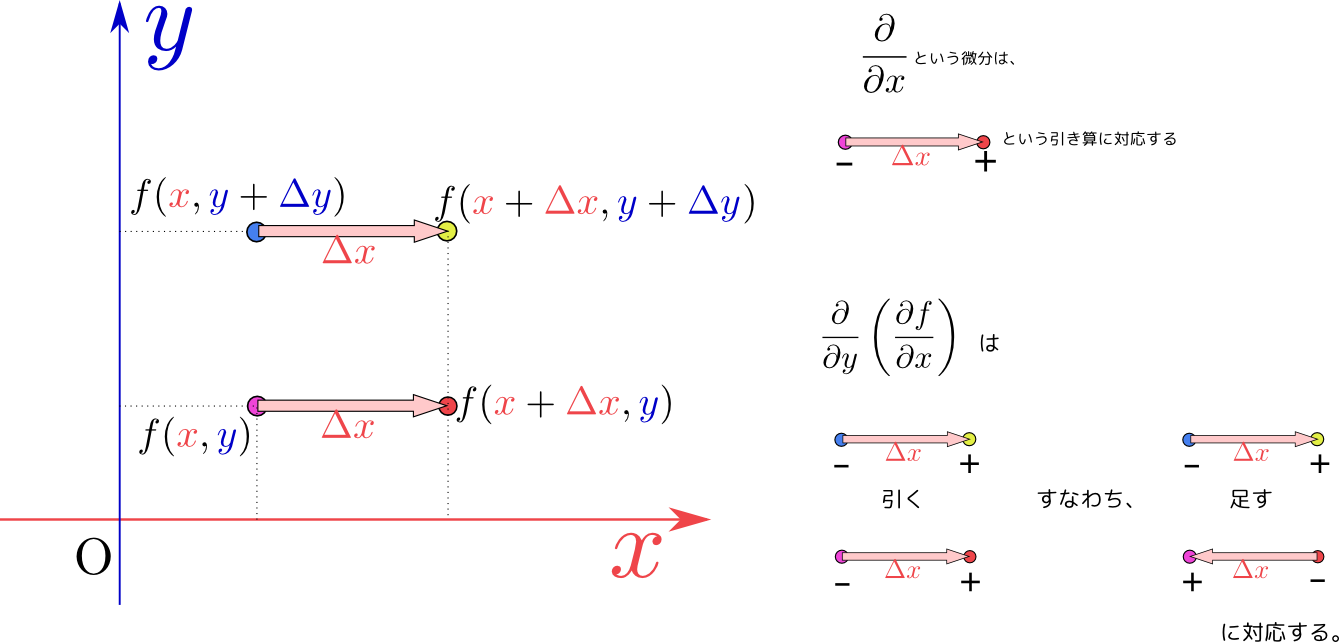
一方、${x}$と${y}$の立場を取り替えた${\partial \over \partial x}\left({\partial f\over \partial y}\right)$は次の図のように書ける。
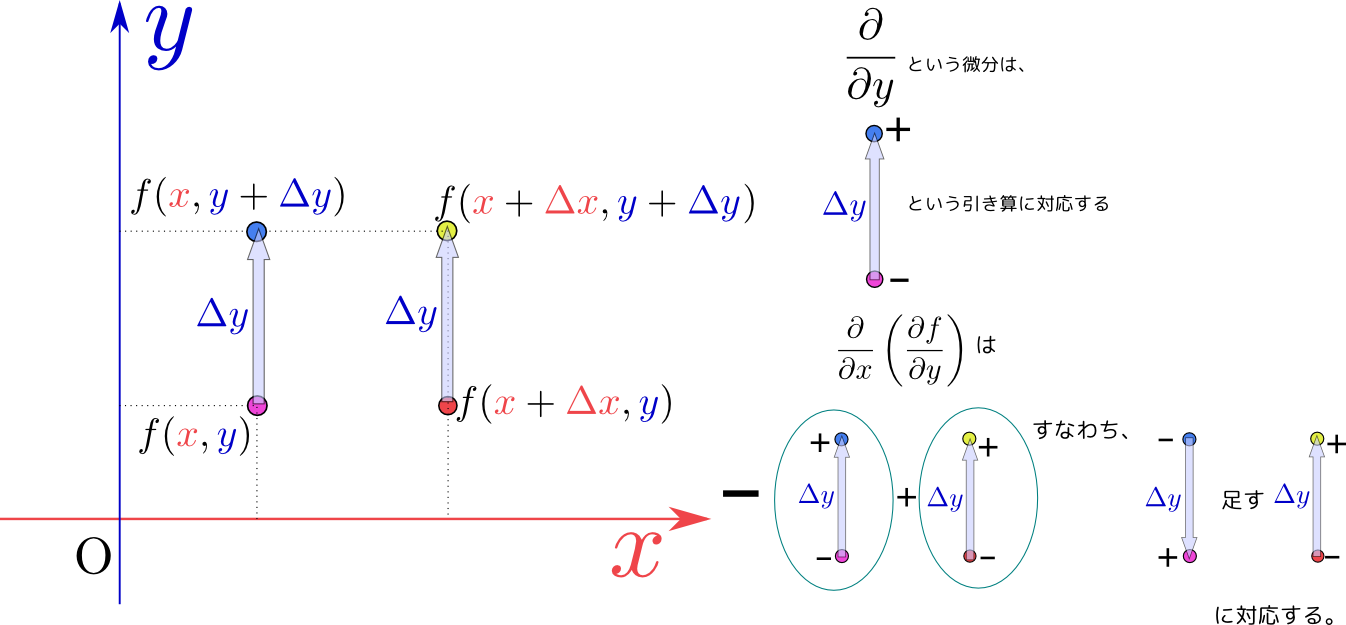
最終的に足したり引いたりしているものは、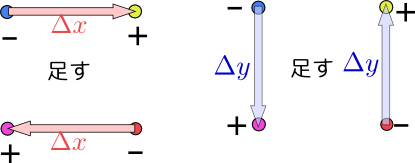
と、同じ量になっているので、二つの微分は同じになる。別の言い方をすると、偏微分$\left({\partial\over \partial x}\fbox{？}\right)_{\!\!{y}}$をする操作と偏微分$\left({\partial\over \partial y}\fbox{？}\right)_{\!\!{x}}$をする操作は交換する。これから、
ということがわかる。よってこの対偶「$P\Rightarrow Q$」に対して「$Qでない\Rightarrow Pでない$」をその対偶と呼ぶ。ある命題が正しければその対偶も正しい。を取れば、
が成立していなかったら、$\mathrm d\left(U({x},{y})\right)=P({x},{y})\mathrm dx+Q({x},{y})\mathrm dy$となる$U$は存在しない
ここで示したのは、「$U$が存在$\Rightarrow$積分可能条件が満たされる」である。この逆「積分可能条件が満たされる$\Rightarrow U$が存在する」も成り立つ。これは、実際に$U$を作ってみれば確かめられる。ここで、
よくある間違い
\begin{equation} U_誤({x},{y}) =\int_{x_0}^{{x}}\mathrm dt P({t},{y}) +\int_{y_0}^{{y}} \mathrm dt Q({x},{t})\label{Umachigai} \end{equation}をしないよう気をつけよう$\int_{x_0}^{{x}}\mathrm dt P({t},{y})$という式を見て、${x}$が入るべきところに${t}$が入っている！」とパニックになってしまう人がたまにいるのだが、別にびっくりするようなことではなく、単に${t}$が（通常${x}$が入っている場所に）代入されているだけのことである。そして、その${t}$という変数が${t}=x_0$から${t}={x}$まで積分されている。積分する間に変化する積分定数${t}$と、積分の上端${x}$は違う量なのだから違う文字を使う。ここで「${x}$に${t}$を代入するのなんて嫌だ」とばかりに$\int_{x_0}^{{x}}\mathrm dx P({x},{y})$などと書いたら混乱が生じてしまう。。
たとえば、${x}\mathrm dx+{y}\mathrm dy=0$という式から「$P={\partial U\over \partial x}={x},Q={\partial U\over \partial y}={y}$」を読み取る。ここで「${x}$で微分して${x}$ということは${1\over 2}{x}^2$、${y}$で微分して${y}$ということは${1\over 2}{y}^2$。この二つを足して$U={1\over 2}{x}^2+{1\over 2}{y}^2$」と考えるのは間違いではない。
しかし、だからと言って、${y}\mathrm dx+{x}\mathrm dy=0$という式から「$P={\partial U\over \partial x}={y},Q={\partial U\over \partial y}={x}$」を読み取り、「${x}$で微分して${y}$ということは${x}{y}$、${y}$で微分して${x}$ということは${x}{y}$。この二つを足して$U=2{x}{y}$」と、同じパターンを繰り返すと間違いなのである。
↑が納得できないという人は検算してみること！
一見「微分は積分の逆だからこれでOK」と思ってしまいがちだが、この$U_誤$を微分すると、
\begin{equation}\left( {\partial U_誤({x},{y})\over \partial x}\right)_{\!\!{y}}=P({x},{y}) +\int \mathrm dt \left({\partial Q({x},{t})\over \partial x}\right)_{\!\!{y}} \end{equation}となってしまって${\partial U\over \partial x}=P({x},{y})$にならない${\partial\over \partial x}\int_{y_0}^{{y}} \mathrm dt Q({x},{t})=\int \mathrm dt {\partial Q({x},{t})\over \partial x}$に注意。${x}$による偏微分${\partial\over \partial x}$は（${y}$を一定としての微分）であるから、$\int_{y_0}^{{y}}\mathrm dt$という積分とは無関係であり、順番を交換してもよい。。${\partial U\over \partial x}=P({x},{y})$とするのに$U$に必要なのは第1項の$\int_{x_0}^{{x}}\mathrm dt P({t},{y}) $だけであって、これ以外に${x}$の関数を付け加えては答があわなくなってしまう。付け加えてもよいのは${y}$の関数のみである。
というわけで、$Q({x},{y})$を含む項を入れるのをやめて、
\begin{equation} U_試({x},{y})=\int_{x_0}^{{x}}\mathrm dt P({t},{y})+f({y}) \end{equation}という関数を試しに作ってみる。この関数は
\begin{equation} \left( {\partial U_試({x},{y})\over \partial x}\right)_{\!\!{y}}=P({x},{y}) \end{equation}を満たす（第2項の$f({y})$は${x}$で偏微分すると消える）。次に${y}$で微分してみよう。
\begin{equation} \left( {\partial U({x},{y})\over \partial y}\right)_{\!\!{x}}=\int_{x_0}^{{x}}\mathrm dt \left({\partial P({t},{y})\over \partial y}\right)_{\!\!{t}} +{\mathrm df\over \mathrm dy}({y}) \end{equation}となる（$f({y})$の微分は偏微分にする必要はないことに注意）。
この結果は$Q({x},{y})$にならなくてはいけない。積分可能条件$\left({\partial P({x},{y})\over \partial y}\right)_{\!\!{x}}=\left({\partial Q({x},{y})\over \partial x}\right)_{\!\!{y}}$を（${x}$のところに${t}$を代入し$\left({\partial P({t},{y})\over \partial y}\right)_{\!\!{t}}=\left({\partial Q({t},{y})\over \partial t}\right)_{\!\!{y}}$に変えてから）使うと、
\begin{equation} \left( {\partial U_試({x},{y})\over \partial y}\right)_{\!\!{x}}=\int_{x_0}^{{x}}\mathrm dt\left({\partial Q({t},{y})\over \partial t}\right)_{\!\!{y}}+{\mathrm df\over \mathrm dy}({y}) \end{equation}となる。ここで、${\partial \over \partial t}$という計算は「${y}$を一定として」という前提のもとでの計算だから、${y}$は定数とみなしてよい。よって、$\int_{x_0}^{{x}}\mathrm dt {\mathrm df\over \dt}({t})=f({x})-f(x_0)$という、定積分と原始関数の関係が偏微分に対しても同様に成り立って、
\begin{equation} \int_{x_0}^{{x}}\mathrm dt\left({\partial Q({t},{y})\over \partial t}\right)_{\!\!{y}}=Q({x},{y})-Q(x_0,{y}) \end{equation}とすることができる（${t}$で微分してから${t}$で定積分した、ということ）。これを使えば
\begin{equation} \left( {\partial U_試({x},{y})\over \partial y}\right)_{\!\!{x}}=\int_{x_0}^{{x}}\mathrm dt\left({\partial Q({t},{y})\over \partial t}\right)_{\!\!{y}}+{\mathrm df\over \mathrm dy}({y})=Q({x},{y})-Q(x_0,{y})+{\mathrm df\over \mathrm dy}({y})\label{Utamesite} \end{equation}を得る。最後の$-Q(x_0,{y})+{\mathrm df\over \mathrm dy}({y})$の分だけ目論見とずれる。そこで、$f({y})$として、「微分すると$Q(x_0,{y})$になる関数」を選べば、ずれがちょうど解消される。そのような関数として$\int_{y_0}^{{y}} \mathrm dt Q(x_0,{t})$を選べば、
\begin{equation} U({x},{y})=\int_{x_0}^{{x}}\mathrm dt P({t},{y}) +\int_{y_0}^{{y}} \mathrm dt Q(x_0,{t})\label{Uintone} \end{equation}である。この$U({x},{y})$は$\left({\partial U({x},{y})\over \partial y}\right)_{\!\!{x}}=Q({x},{y})$を満たす。${y}$のみの関数を付け加えたのだから、$\left({\partial U({x},{y})\over \partial x}\right)_{\!\!{y}}=P({x},{y})$の方もそのまま成り立っている。
なお、ここでやった計算で${x}$と${y}$の役割を逆転させれば、
\begin{equation} U({x},{y})=\int_{x_0}^{{x}}\mathrm dt P({t},y_0) +\int_{y_0}^{{y}} \mathrm dt Q({x},{t})\label{Uinttwo} \end{equation}という式が作られる。これも正しい$U({x},{y})$である。微分してみると、
\begin{equation} \begin{array}{rl}\left( {\partial U({x},{y})\over \partial x}\right)_{\!\!{x}} =&P({x},y_0)+\int_{y_0}^{{y}}\mathrm dt \left({\partial Q({x},{t})\over \partial x}\right)_{\!\!{t}}\\[4mm] =&P({x},y_0)+\int_{y_0}^{{y}}\mathrm dt \left({\partial P({x},{t})\over \partial t}\right)_{\!\!{x}}\\[4mm] =&P({x},y_0)+P({x},{y})-P({x},y_0)=P({x},{y}) \end{array} \end{equation}となって、ちゃんと$U({x},{y})$の満たすべき条件を満たしている。
この二つの積分が「どの場所の何を積分しているか」を図で表したものが次のグラフである。
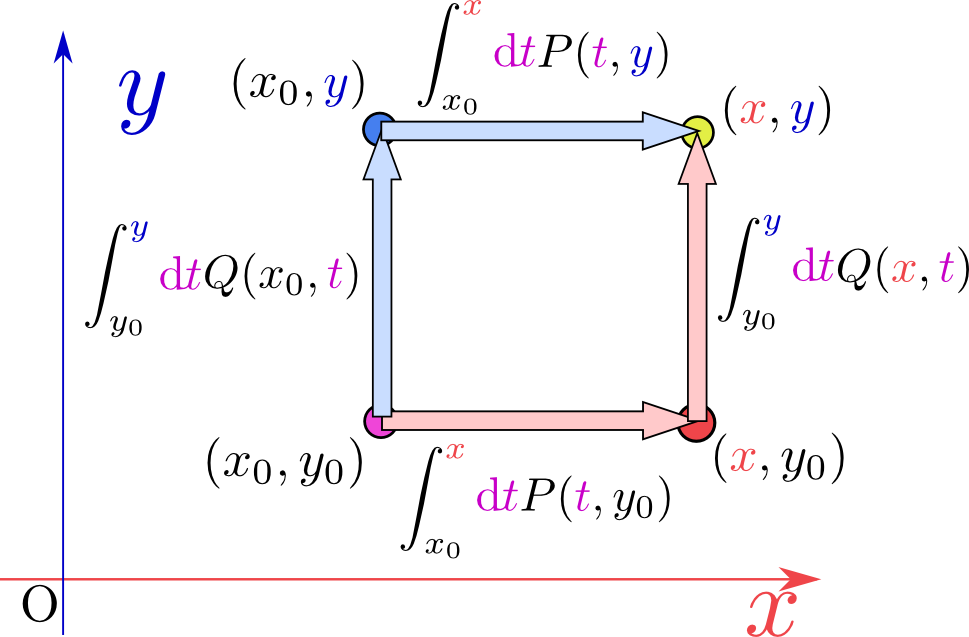
場所$({x},{y})$における$U$を求めるために、一方はまず右へ$\to({x},y_0)$進んでから上へ$\to({x},{y})$と進む。もう一方はまず上へ$\to(x_0,{y})$へ進んでから右へ$\to({x},{y})$進んでいる。この二つの積分結果が同じになることが積分可能条件そのものなのである。「微分の逆が積分」ということは何度か述べているが、常微分で成立した$\int_a^b {\mathrm df\over \mathrm dx}({x}) \mathrm dx=f(b)-f(a)$という式を偏微分の時に使おうとすると、「積分ってどの積分？（${x}$方向？、${y}$方向？、斜め？…曲線でもいいし）」という問題が生じてくる。積分可能条件が成立してればそこは気にしなくてよい。
【授業後に出た質問↓】
以上からわかるように、ある微小量があったとき、それが全微分であるかどうかというのは非常に大事である。ある量が微小量で、かつ全微分である量であったとすれば、そのある量を$\mathrm dX$と書いて、「微分される前の量」である$X$を定義することができる。そうやって定義された$X$は、「変化のさせ方にはよらず、変化後の状態だけで決まる量（状態量）」になり、便利である。
いったん「状態量」であることが証明された量は、「これまでどんな変化をしてきたか」という経歴を一切考慮することなく「今どうなっているか」だけを見て計算し表現することができる。たとえばエネルギーなどがこれにあたる（例えば「この物体が昨日どこにいたかを知らないとこの物体の位置エネルギーは計算できない」と言われたらどれだけ面倒くさいことになるか、と想像してみればよい。エネルギーが状態量であることの有難味がわかる）。ある微小量が全微分となり、対応する状態量が定義できる（逆にいえば、これを微分すれば最初考えていた「ある微小量」が出て来る）という状況は、たいへん有り難い状況なのである。
一方、微小量ではあるが全微分ではない量（もちろんこういう量も存在する！）についてはこれができないから、対応する状態量を定義できない 例としては「熱」がある。気体をある状態から微小に違う別の状態に変化させる時に、微小な熱が移動することになるが、一般的には変化のさせ方で移動する熱量は変わる。だから、「微分すると熱になる量」は特別な場合を除けば定義できない。。そういう量は$\mathrm dy 'X$のように${}'$をつけて「全微分じゃないよ」ということを表すこともある。