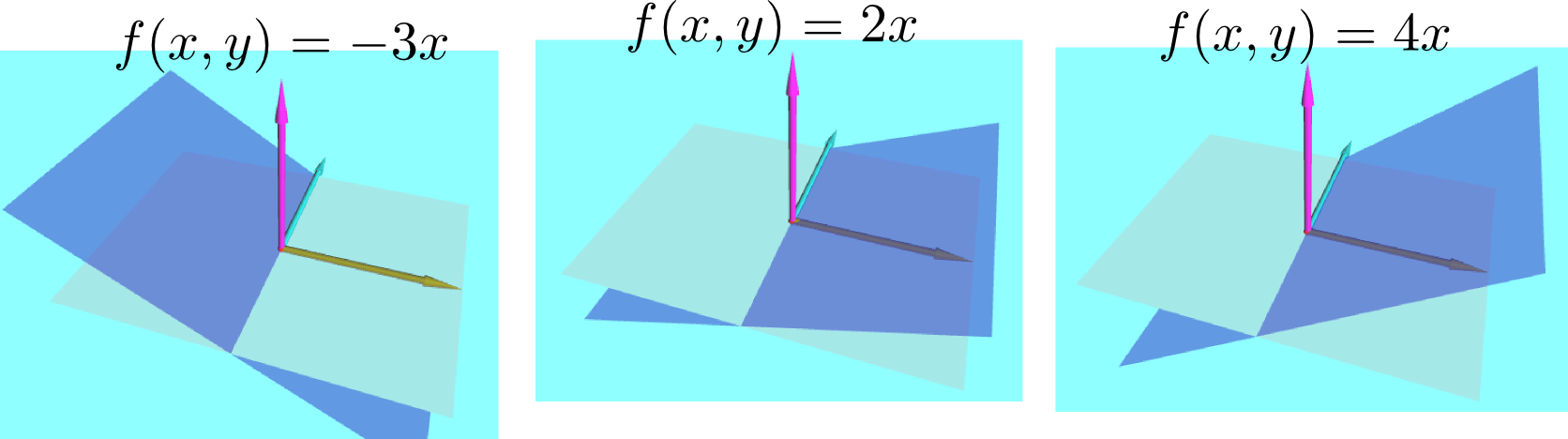
方向微分
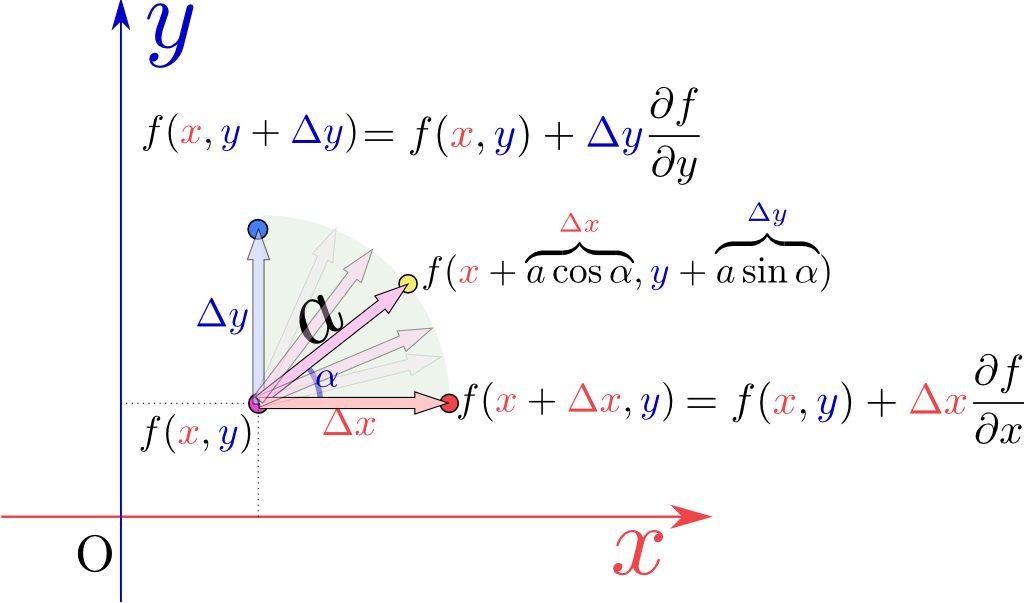
2変数の場合で話をする。
$f({x},{y})$の「偏係数」は$\left({\partial f({x},{y})\over \partial x}\right)_{\!\!{y}}$と$\left({\partial f({x},{y})\over \partial y}\right)_{\!\!{x}}$の二つがある(「偏微分係数」と呼ぼう)。この二つは「${x}$方向に移動した場合」「${y}$方向に移動した場合」の微小変化の微分係数である。こう考えると「斜めに移動した場合の微係数だって考えていいではないか」という気分になるのは当然である。そこで、図のように傾いた方向に$a$だけ動いた場合の変化を考えよう。つまり、$\Delta x=a\cos\alpha,\Delta y=a\sin \alpha$と選ぶわけである。こうしておいて$f$の変化量を計算したのち、結果を移動量(今の場合$a$)で割ってから極限を取ると、
\begin{equation}
\lim_{a\to0}{
f({x}+ \overbrace{a\cos\alpha}^{{\Delta x}},{y}+\overbrace{a\sin\alpha}^{{\Delta y}})-f({x},{y})\over a
}
=\left({\partial f({x},{y})\over \partial x}\right)_{\!\!{y}} \cos\alpha
+\left({\partial f({x},{y})\over \partial y}\right)_{\!\!{x}} \sin\alpha\label{houkoubibun}
\end{equation}
となる。この微分は角度$\alpha$で表される方向への「方向微分」と呼ぶ。この式はベクトル$\left(\left({\partial f({x},{y})\over \partial x}\right)_{\!\!{y}},\left({\partial f({x},{y})\over \partial y}\right)_{\!\!{x}}\right)$とベクトル$\left(\cos \alpha,\sin \alpha\right)$の内積になっている。
関数$f({x},{y})$を決めれば、各点各点でのベクトル$\left(\left({\partial f({x},{y})\over \partial x}\right)_{\!\!{y}},\left({\partial f({x},{y})\over \partial y}\right)_{\!\!{x}}\right)$が決まる。そしてそのベクトルは場所によって違ういろんな方向を向いている。$\left(\cos \alpha,\sin \alpha\right)$を様々な方向に向ければ方向微分の大きさが
\begin{equation}
- \sqrt{
\left({\partial f\over \partial x}\right)^2+
\left({\partial f\over \partial y}\right)^2}
\leq
\left({\partial f\over \partial x}\right) \cos\alpha
+\left({\partial f\over \partial y}\right) \sin\alpha
\leq
\sqrt{
\left({\partial f\over \partial x}\right)^2+
\left({\partial f\over \partial y}\right)^2}
\end{equation}
の範囲で変化する(長くなるので引数$({x},{y})$等を省略した)。特別な場合として
- 方向微分が0になる場合:この場合、二つのベクトルは直交している。
- 方向微分の大きさが最大になる場合:この場合、二つのベクトルは同じ方向を向く。
という二つの場合を考えよう。
方向微分が0になる場合の$\left(\cos \alpha,\sin \alpha\right)$と、方向微分が最大となる場合の$\left(\cos \alpha,\sin \alpha\right)$は直交している。山の斜面に立ったとき「傾きがない方向(等高線に沿って移動する方向)」と「傾きが最大の方向(山を登る方向)」は常に直交している、ということになる。
たとえば前に考えた$f({x},{y})=\sqrt{{x}^2+{y}^2}$という関数の場合、偏微分係数の作るベクトルは
\begin{equation}
\begin{array}{rl}
& \left(\left({\partial f({x},{y})\over \partial x}\right)_{\!\!{y}},\left({\partial f({x},{y})\over \partial y}\right)_{\!\!{x}}
\right) =\left(
{{x}\over\sqrt{{x}^2+{y}^2} }
,
{{y}\over\sqrt{{x}^2+{y}^2} }
\right)
\end{array}
\end{equation}
である。
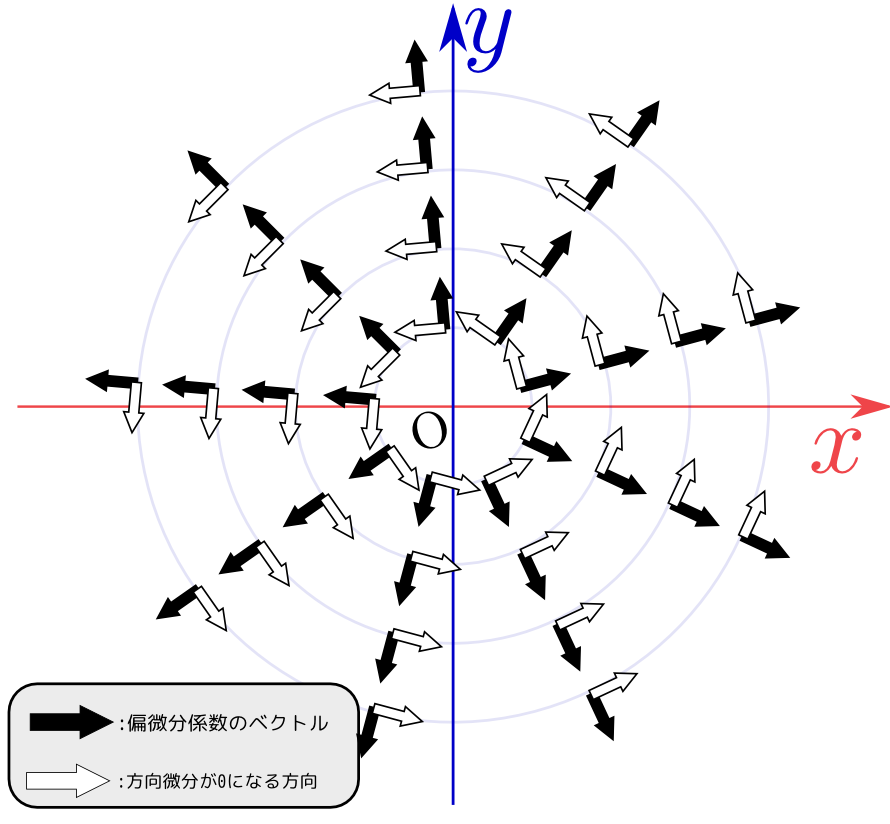
↑の図に示した黒矢印がこの偏微分係数のベクトルである(各点ごとに違う方向を向く)。一方、これに垂直なベクトルを白矢印で示した。白矢印の方向は「$\sqrt{{x}^2+{y}^2}$のこの方向への微分が0になる方向」すなわち、「$\sqrt{{x}^2+{y}^2}$が変化しない方向」である(今の場合は$\sqrt{{x}^2+{y}^2}$が原点からの距離であることを思えば自明)。
この偏微分係数のベクトル(gradと呼ばれることもある)
↓はマウスで動かせる$r$方向のベクトルと$\theta$方向のベクトルの図である。
x=2,
y=2,
r=2.82842712474619,
θ=0.78539816339745,
(∂/∂r)=0.70710678118655(∂/∂x)+0.70710678118655(∂/∂y)
(1/r)(∂/∂θ)=0.70710678118655(∂/∂x)+0.70710678118655(∂/∂y)
下に座標が出ているので確認しておこう。最後に偏微分と偏微分の関係もついているが、それは来週講義する。
極大・極小
1変数関数の極大・極小点では微分が0になったが、多変数(ここでは「2変数」のみを扱う)関数の場合も微分が0の点が極大極小点になるのは同じである。ただし、多変数なら「微分の方向」があるので「ある方向の微分は0だが、別の方向では0でない」ということが起こりえる。
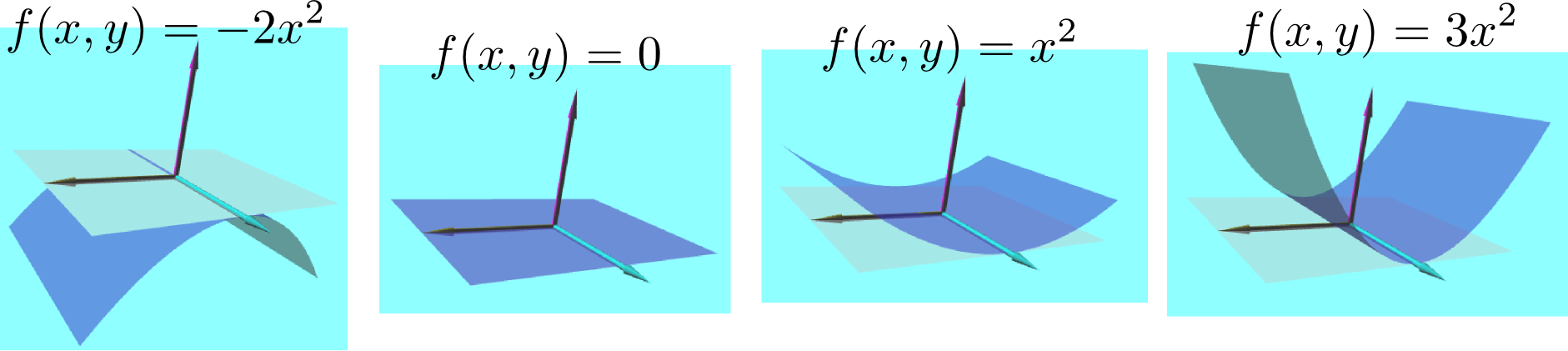
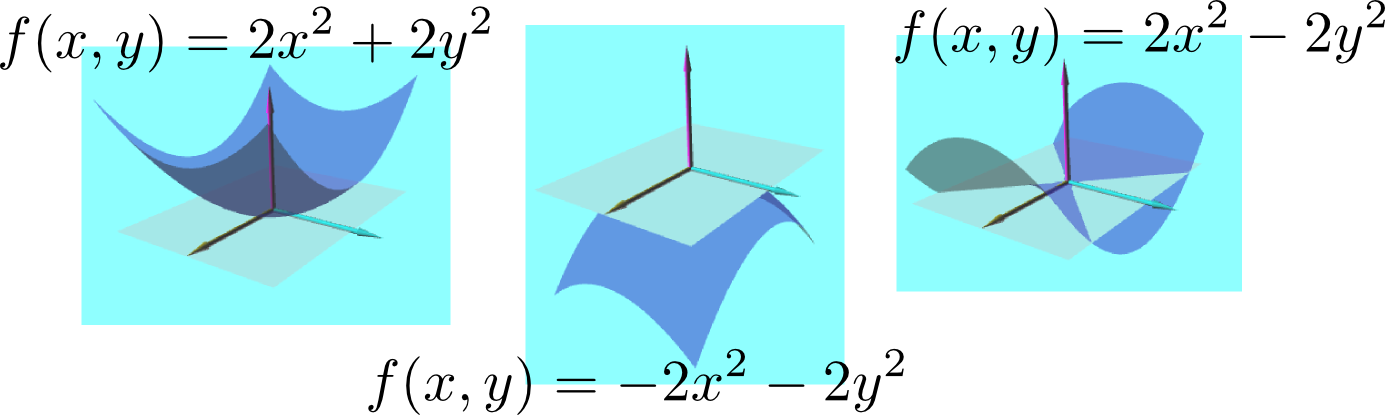
次の図に示したのは$f({x},{y})={x}^2+{y}^2,-{x}^2-{y}^2,{x}^2-{y}^2$の三つの関数の3次元グラフで、どの場合も原点においてどの方向の微分も0であるが、二階微分の値の正負が違う。
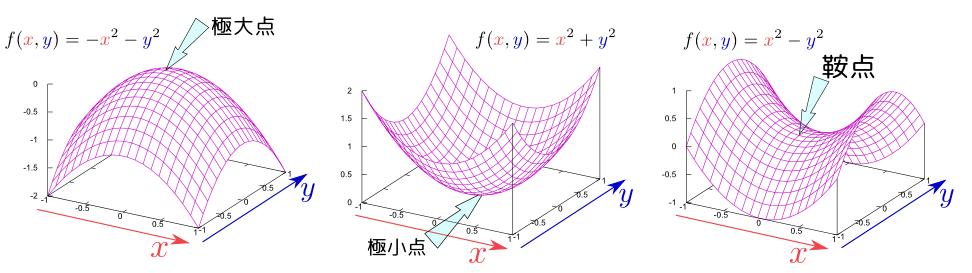
どの方向に対しても一階微分が0で二階微分が負なら、それは極大点である。逆に、どの方向に対しても一階微分が0で二階微分が正なら、それは極小点である(ここまでは1変数の時の素直な拡張である)。多変数で現れる新しい状況として「一階微分はどの方向に対しても0であるが、二階微分の正負は方向により異なる」という場合があり、この場合は(図に示したように馬の鞍の形なので)「鞍点」と呼ぶ。
上の図では示してないが、ある方向の二階微分が0であるという状況ももちろんある。というより、鞍点の場合「二階微分が正である方向」と「負である方向」があるのだから、その境界の方向では二階微分は必ず0になる。
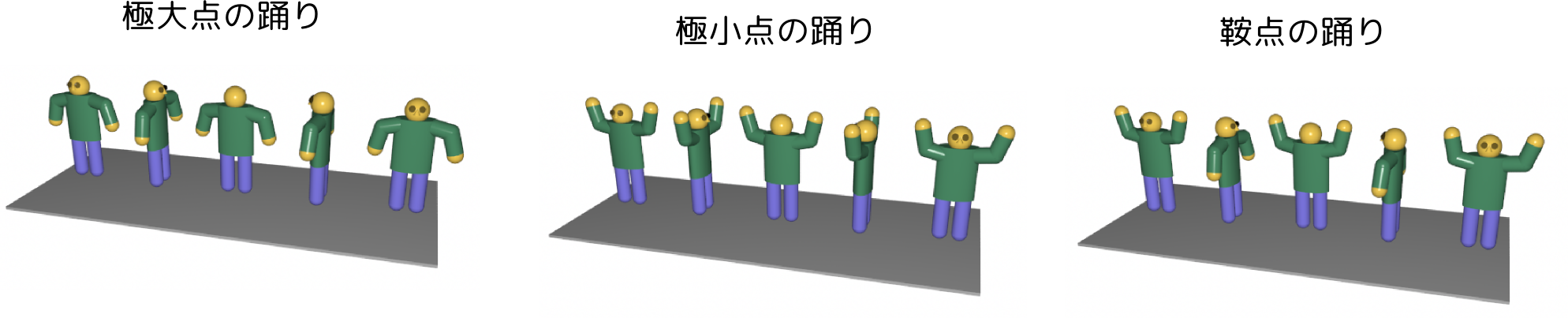
↓は極大点・極小点・鞍点の違いをイメージするために教室で見せた踊り。ぐるぐる周りながらそれぞれの状況の応じて手を上下して山や谷を作る。
上では比較的単純な例を提示したので、${\partial^2 f\over \partial x^2}$と${\partial^2 f\over \partial y^2}$の正負を見て場合分けできたが、2変数関数の二階微分はもう一つ、${\partial^2 f\over \partial x\partial y}$があることを忘れてはいけない(上の例では全て${\partial^2 f\over \partial x\partial y}=0$なので気にしなくてもよかった)。

逆に${\partial^2 f\over \partial x\partial y}\neq0$である例として、$f({x},{y})={x}{y}$を考えてみると、この場合も鞍点になっている。
一般の2変数関数で、一階微分が全て0である点(このような点は「\newwordruby{ていりゅうてん}{停留点}」と呼ぶ)が見つかったとして、その点が極大なのか極小なのかそれとも鞍点なのかを知りたい場合は、次の節で考える多変数関数のテイラー展開の2次の項を調べる必要がある。
多変数関数のテイラー展開
1変数の関数$f({x})$のテイラー展開
\begin{equation}
f({x})=f(a)+f'(a)({x}-a)+{1\over 2}f''(a)({x}-a)^2+{1\over 3!}f'''(a)({x}-a)^3+\cdots
\end{equation}
は「点${x}=a$における0階微分、1階微分、2階微分、$\cdots$が同じになる多項式を作る」という手順(両辺を${x}$で微分してから${x}=a$を代入すると一致する)で見つけることができたから、同様に考えると、
2変数関数のテイラー展開
\begin{equation}
\begin{array}{rl}
f({x},{y})
=&f(a,b)
+{\partial f\over \partial x}({x}-a)
+{\partial f\over \partial y}({y}-b)\\
+&{1\over 2}{\partial^2 f\over \partial x^2}({x}-a)^2
+{\partial^2 f\over \partial x\partial y}({x}-a)({y}-b)
+{1\over 2}{\partial^2 f\over \partial y^2}({y}-b)^2
\\
+&{1\over 3!}{\partial^3 f\over \partial x^3}({x}-a)^3
+{1\over 2}{\partial^3 f\over \partial x^2\partial y}({x}-a)^2({y}-b)
+{1\over 2}{\partial^3 f\over \partial x\partial y^2}({x}-a)({y}-b)^2
+\cdots
\end{array}
\end{equation}
のようになる。スペースが足りないので省略して書いているが、すべての偏微分は$({x},{y})=(a,b)$での値である(${x}$で偏微分する時は${y}$は一定とする。逆も同様)。
実際に、微分の結果が一致することを確認してみよ。
一般項を和記号で表現すると
\begin{equation}
f({x},{y})=\sum_{m=0}^\infty\sum_{n=0}^\infty {1\over m! n!}{\partial^{m+n} f({x},{y})\over \partial x^m \partial y^n}\biggr|_{{x}=a\atop {y}=b}({x}-a)^m({y}-b)^n
\end{equation}
である。1変数の時と同様に、和を途中で打ち切る場合には余剰項が出る。また、テイラー展開には有効な範囲(収束半径)があることも1変数の場合と同様である。
前節最後で述べた「停留点が極大・極小・鞍点のどれになっているかを判定する方法」をここで考えよう。$(a,b)$が停留点とすればそこで一階微分は0だから、$({x}-a)={\Delta x},({y}-b)={\Delta y}$と書けば、
\begin{equation}
f({x},{y})
=f(a,b)
+\underbrace{\overbrace{{1\over 2}{\partial^2 f\over \partial x^2}}^a({\Delta x})^2
+\overbrace{{\partial^2 f\over \partial x\partial y}}^b{\Delta x}{\Delta y}
+\overbrace{{1\over 2}{\partial^2 f\over \partial y^2}}^c({\Delta y})^2}_{曲がり具合を表現する部分}
+\cdots
\end{equation}
となる。3次以上の項は省略した。式に示したように、係数を以下$a,b,c$で表す。
上の「曲がり具合を表現する部分」がどのような${\Delta x},{\Delta y}$に対しても正であるならばこの点は極小点、逆に常に負ならば極大点である。正にも負にもなる場合は鞍点だと言える(他の可能性としては正、負ではなく0以上や0以下という可能性もある)。この式は
\begin{equation}
a({\Delta x})^2 + b{\Delta x}{\Delta y}+c({\Delta y})^2
=\underbrace{({\Delta y})^2}_{常に正}\underbrace{
\left(
a\left({{\Delta x}\over{\Delta y} }\right)^2
+b{{\Delta x}\over{\Delta y} }+c
\right)}_{この部分の正負が問題}
\end{equation}
となるから、後は「二次式$ax^2+bx+c$の正負を場合分けせよ」という問題になり、二次方程式の判別式を使うこととで状況を分類することができる。結果は以下の通り。

- $b^2-4ac>0$ の場合: 正にも負にもなる(鞍点)
- $b^2-4ac<0$ かつ $a>0$の場合: 常に正(極小点)
- $b^2-4ac<0$ かつ $a<0$の場合] 常に負(極大点)
この判別式$b^2-4ac$というのは実は$\left(\begin{array}{cc}{\partial^2 f\over \partial x^2}&{\partial^2 f\over \partial x\partial y}\\{\partial^2 f\over \partial y\partial x}&{\partial^2 f\over \partial y^2}\end{array}\right)$という行列(「ヘッセ行列」と呼ぶ)の行列式の$-4$倍である。行列の形で書くと、3変数以上の場合にも拡張できる。