はじめに

　今日は指数関数の続きから、対数関数を経て微分のイントロダクションに続く。

---

目次

　プログラムについて御質問、御要望、バグ報告などございましたら、前野［いろもの物理学者］昌弘へメールくださるか、または、twitterにてirobutsuまでメンションしてください。

第４講に戻る 講義録目次に戻る

指数関数（続き）

指数関数の傾きとネイピア数

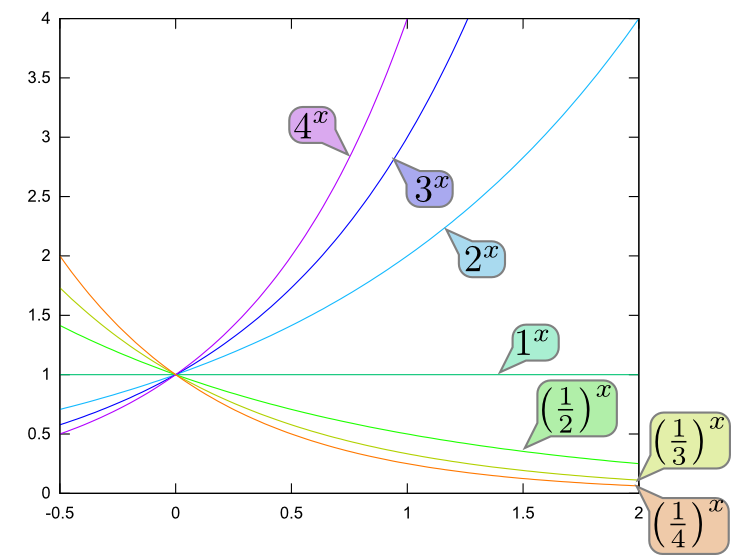
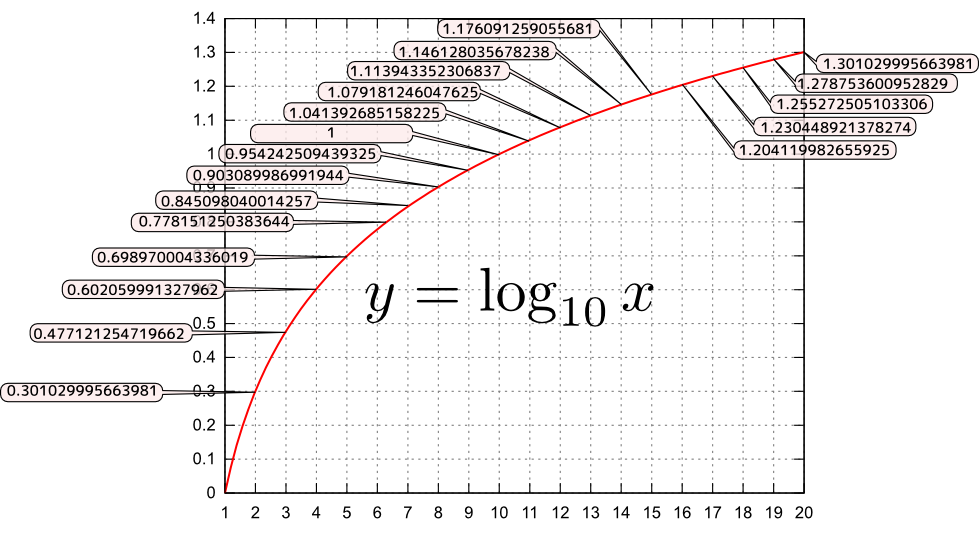
　底が大きくなると指数関数は増加の度合いが大きくなる。$a$が1より小さい場合は、むしろ減少する関数となる。

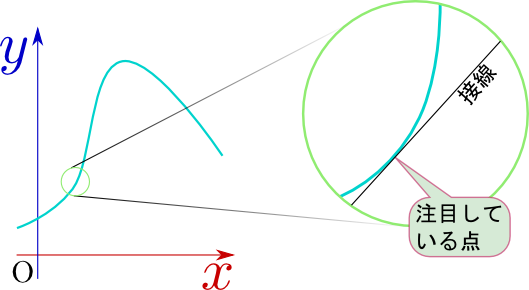
　本講義ではここまででも何度か強調しているが、「関数のある点の近傍でのふるまい」を考えることは重要である。そこで指数関数の原点付近でのふるまいを見ておこう。

　グラフにも示されているように、$x=0$のときの$y=a^{x}$の値はすべての$a$で等しく1である。一方、$x=0$でのグラフの傾きは、底$a$が大きいほど大きい。そこで、この傾きがちょうど1になるところの$a$を探す。そのときの$a$を e と書いて「ネイピア数(Napier's constant)」もしくは「自然対数の底」と呼ぶ対数とはなにかは、まだ説明してない。言葉の定義の順番が混乱しているのは許して欲しい。。シンプルに e （いー）と呼んでいることも多い変数$e$と区別するために、 e は立体で書く（イタリックにしない）ことにする。。

　e の値を知る方法について考えよう。下の図は$y=2^{x}$と$y=3^{x}$と、傾き1で$(0,1)$を通る直線$y=x+1$のグラフである。

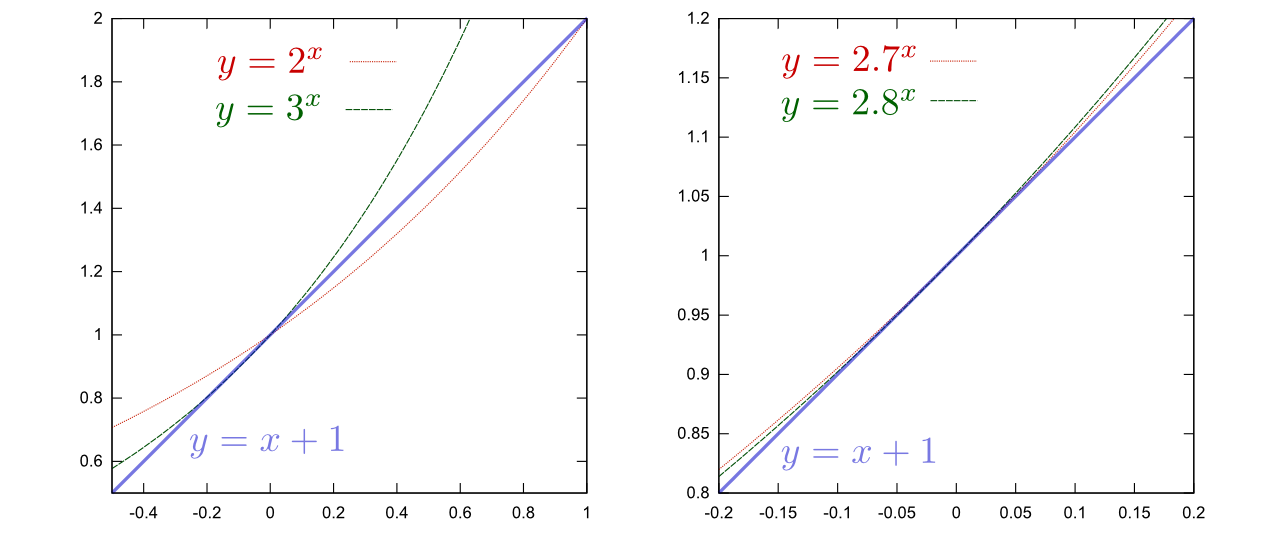
　これを見ると、$x=0$で傾き1になるためには、2よりは大きく3よりは小さい数を底にしなくてはいけない。数字をどんどん細かくしていきながら考えていく。たとえば次の段階では、$y=2.7^{x}$と$y=2.8^{x}$のグラフの間に直線$y=x+1$があることから、 e が2.7より大きく2.8より小さいことがわかる。この手続を繰り返すことで、 e の値を精密にしていくことができるだろう（グラフは重なってしまってわかりにくいが）。

　こうやって求めた e の大きさは e=2.718281828459045… である。この e は無理数であることが証明されていて、無限に続く小数である。この値をどうやって計算するのかについては、ここでは「いろんな値を入れてグラフを描いていき、傾きが1になるところを探せば e は計算できるだろう」という程度の大雑把な理解にとどめておこう。実際にはこんな面倒なことはやらない。実際的で、かつ大雑把でない理解のために微分という計算が必要になる。

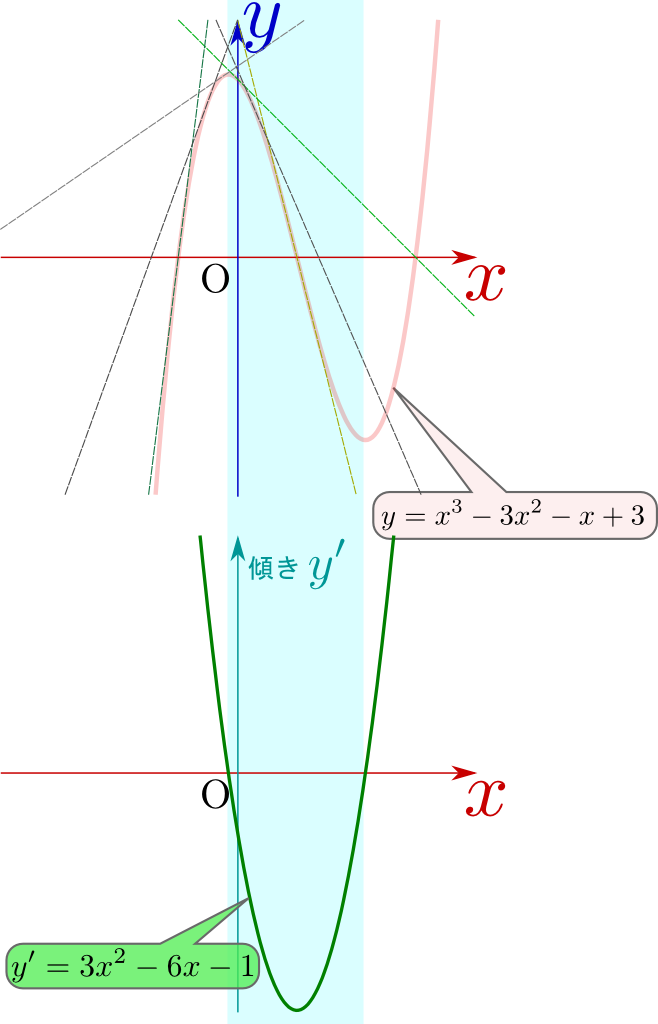
　なぜ傾き1がそんなに大事なのかについては後でわかるが、ここでは「傾きはすなわち微分であり、微分を知ることが自然法則を知る手がかりになる」ということを思い出しておこう。

電卓でeを計算する方法

　上のようにして e が計算できる理由は、後で出てくる（だからまだわからなくてもよい）、

\begin{equation} {\mathrm e}^x = 1+x+{x^2\over 2!}+{x^3\over 3!}+{x^4\over 4!}+{x^5\over 5!}+\cdots\label{extenkai} \end{equation}

という式（${\mathrm e}^x$のテイラー展開の式）があって、この式に$x=1$を代入すると、

\begin{equation} {\mathrm e} = 1+1+{1\over 2!}+{1\over 3!}+{1\over 4!}+{1\over 5!}+\cdots \end{equation}

になるからである。\式{extenkai}がどうやって出てくるかは後のお楽しみであるが、とりあえず${\mathrm e}^{x}=1+x+\cdots$までは「$x=0$での値が1で傾きが1」ということからわかる。

　この特別な数字 e を使った指数関数$y={\mathrm e}^{x}$は、「微分方程式を解く」という作業において頻出する。そこでこれを特に、$y=\exp(x)$のように書くこともある。$\exp$は「イクスポーネンシャル」と読む${\mathrm e}^{x}$を「イクスポーネンシャルエックス」のように読むこともある。。

指数関数の底の変換

$y=2^{x}$という関数と$y=4^{{X}}$という関数を考えよう。${X}=2x$ならばこの二つが等しい、すなわち

\begin{equation} 2^{2{X}}= (2^2)^{X}=4^{X} \end{equation}

である（たとえば、$2\times 2\times 2\times 2=(2\times 2)\times(2\times 2)=4^2$）。今は2と4という単純な例で考えたが、もっと一般的に$y=a^x$と$y=b^{X}$の関係を考えよう。たとえば、$a$と$b$の間に$a=b^c$（$c$もまた別の定数）という関係があるなら、

\begin{equation} a^x= (b^c)^x=b^{cx} \end{equation}

となるから、${X}=cx$とすればこの二つの関数が同じ関数になる。

　指数関数の底はいろんな値を使ってよいのだが、日常計算においては$y=10^x$のように10が使われることが多い。一方、コンピュータや情報科学の世界では$y=2^x$のように2がよく使われる。

　これも後でわかることだが、微分や積分などを行う時には e を底にした指数関数$y={\mathrm e}^x$がもっとも使いやすい。よってこれらを互いに変換する必要がある。その時に

指数関数の底を変える

という方法を使う。たとえば$10=2^{3.321928094887362\cdots}$なので$10^3=1000,2^{10}=1024$だから$10^3\fallingdotseq2^{10}$である（コンピュータの世界で「キロ」と言ったら1000ではなく1024を指すことが多い）。ゆえに$10\fallingdotseq 2^{10\over3}$。、

\begin{equation} 10^{x}=2^{(3.321928094887362\cdots)\times x} \end{equation}

となる。この${3.321928094887362\cdots}$という数字は10は2の何乗か？という疑問の答えであるが、それも一つの関数である。この関数は次の節で考える。

「はじめに」に戻る。　「対数関数」へ

対数関数

対数関数の定義：指数関数の逆関数

前節の最後で10は2の何乗か？という疑問を考えた。より一般的に${x}$は${a}$の何乗か？という問題を考えることにしよう。つまり、${x}=a^{y}$という式が成り立つときに、${y}\to{x}$という対応関係を知りたい。つまり今考えたい関数は指数関数${y}=a^{x}$の逆関数であり、これを「対数関数」と呼ぶ。対数関数を表現するには、$\log$という記号を使う。一般的定義は

対数関数

$\log_a$の$a$のことを指数関数の時と同様、「底（てい）」と呼ぶ。底が$2,{\mathrm e},10$およびその逆数${1\over 2},{1\over {\mathrm e}},{1\over 10}$の場合の指数関数（実線）と対数関数（破線）のグラフを下に示した（互いに逆関数になっていることを確認せよ）。

　左右を見比べると、指数関数の性質$a^{-{x}} = \left({1\over a}\right)^{{x}}$ということが（${x}\to-{{x}}$という変化がグラフ上では左右反転となって）見て取れる。対数関数はこれの逆関数（${x}$と${y}$の立場が入れ替わる）だから、

\begin{equation} \log_a {x} = -\log_{1\over a}{x} \end{equation}

という関係がわかる（グラフでは上下反転として読み取れる）。

　上の青い線が対数y=log_ax、薄い赤の線が指数関数y=a^xのグラフである。

この二つが互いに逆関数であることを確認しよう。

青い線：y=log_2.0x

薄い赤い線：y=2.0^x

　指数関数と対数関数は逆関数である。しかし、$\log_a\left(a^{x}\right)=x$はどんな実数${x}$に対しても成り立つが、$a^{\log_a {x}}={x}$は、${x}\geq0$でないと今の段階では定義できていない（負の数の$\log$をちゃんと定義した後でなら考えられる）。

対数関数の公式

　指数関数が持っていた「$\mathrm e^{{x}}$の肩の${x}$の足算は掛算になる」という性質は、対数においては逆になり、以下の式が成り立つ。

$\log$の引数の${掛算\atop 割算}$は$\log$の${足算\atop 引算}$になる

　上の式が確かに成り立つことは、$a^{\log_a(x_1x_2)}=x_1x_2$という式に$x_1=a^{\log_a x_1}$と$x_2=a^{\log_a x_2}$を代入してみれば、

\begin{equation} a^{\log_a(x_1x_2)}=a^{\log_a x_1}\times a^{\log_a x_2} \end{equation}

となるからわかる。

　また、$(a^{x_1})^{x_2}=a^{x_1x_2}$となることから逆に、

冪の対数は底の対数の指数倍

もわかる。

　なかなか対数関数（$\log$）の「気持ち」がわからない、という人のために$10^{x}$を例にして説明しよう。

　$10^2=100$は0が2桁、$10^3=1000$は0が3桁、$10^4=10000$は0が4桁、と増えていくことを考えると、${y}=10^{{x}}$という関数は

$n$を入れると「1の後ろに0が$n$個並んだ数」が出てくる関数この関数が定義できるためには「$n$は0以上の整数」ということになるから、任意の実数を定義域とする${y}=10^{{x}}$より定義域が狭くなってしまっている。

であるとも言える。ここで逆関数である${x}=\log_{10}{y}$は

「1の後ろに0が$n$個並んだ数」を入れると$n$が出てくる関数

という関数になる。すなわち、$10\to1,100\to2,1000\to3,\cdots,100000000\to8,\cdots$のような対応関係（言わば、「桁数$-1$を求める関数」である）が、${x}=\log_{10}{y}$という関数が表現する対応関係の「一部」である（実際には${x}=\log_{10}{y}$の${y}$には正の実数負だとどうなるのかは、またこの先で。なら何を入れてもよいから、もっと広い範囲で使える）。

　「車の修理代が6桁もかかったわ〜」「え〜っ」のように、数字の大きさを「○桁」で表現することはないだろうか。あれが$\log$の考え方なのである。

　対数関数は「掛算の簡略化」にも使える。たとえば$1000\times 1000=1000000$だが、これを「0が3桁ある数字と0が3桁ある数字を掛けたから、0が6桁ある数字になる」という計算をすることができる。こう考えると、積の対数関数を対数関数の和に直す式を、

\begin{equation} \log_{10} \underbrace{1000000}_{0が6つ}=\log_{10}\underbrace{1000}_{0が3つ}+\log_{10}\underbrace{1000}_{0が3つ} \end{equation}

のように理解できる。

　このやり方は$10^n$（$n$が整数）の場合しかできないが、そうでない場合に拡張することはできる。なお、$\log_{10}{x}$のように底を10にした対数関数を「常用対数(common logarithm)」と呼ぶ。$\mathrm e$を底にした対数関数$\log_{\mathrm e}{x}$は「自然対数(natural logatithm)」である。以後、$\log{x}$のように底を省略した場合は自然対数である「自然（natural）」のnを取って、$\log_{\mathrm e} {x}=\ln {x}$のように書くこともある。。

　下に、${y}=\log_{10}{x}$の、${x}=1$から${x}=20$までのグラフを示した。

　図を見て、たとえば$\log_{10}2+\log_{10}3=\log_{10}6,\log_{10}2+\log_{10}5=1$あるいは$\log_{10}9=2\log_{10}3$などのように、「掛算が足算に翻訳されること」を確認しようこんなふうに具体的な数で「対数」というものの勘所をつかむことも重要。この図を見てしばらく「遊ぶ」ぐらいに対数に親しんで欲しい。。

$\log_{10}$の値を前もって調べておくことができると、例えば$5343342\times234234234$という計算を

\begin{equation} \log_{10} \left(5343342\times234234234\right) =\underbrace{\log_{10} 5343342}_{6.7278\cdots} + \underbrace{\log_{10} 234234234}_{8.3696\cdots} \fallingdotseq15.0974\label{daitailog} \end{equation}

のように、対数を介することで足算を使って実行できる。逆に$10^{15.0974}$を計算すれば、1251411091802385を得る。この値は、真面目に計算した結果の1251593620370028と比べて、４桁めまで正しい足算の結果を15.0974と小数点以下4桁までしか計算していないので、この程度の精度なのは仕方ない。}。今なら電卓なりコンピュータなりで計算するが、昔はいろんな数とその対数の表（「対数表」）が作ってあって、それを使って掛算をしていた対数で目盛を打った物差しのようなもの（計算尺）を使って計算したりもしていた。。

　対数関数は「桁数で比較する」という感覚で使われるわけだが、これは概算しているというわけではなく、大きさの変化があまりに大きい物を比較する時に便利な方法であるとも言える。たとえば地球の質量は$5.97\times 10^{24}$ kg、太陽の質量は$1.99\times 10^{30}$ kgである。これを普通の数字で書けば

\begin{equation} \begin{array}{rr} 地球の質量：&約597000000000000000000000000 {\rm ~kg} \\ 太陽の質量：&約1990000000000000000000000000000000 {\rm ~kg} \end{array} \end{equation}

なのだが、こう書かれるよりむしろ$10^？$の形で書いて肩に乗った24や30を見た方が「ああ約$10^6$倍程度違うんだな」ということが実感しやすい（というより、そういう感覚を持てるようにならないと、大きさの違いが甚だしい量を比較できるようになれない）。

対数関数の底の変換

　指数関数同様、対数関数も底を変換したいことがよくある。

　指数関数の底は$a=b^c$の時、$a^{x}=b^{c{x}}$のように変換したから、${y}=a^{x}=b^{c{x}}$とおいて、$\log_a{y}$と$\log_b{y}$を計算すると、

\begin{equation} \log_a {y}= {x}, ~~~\log_b {y}= c{x} \end{equation}

という式が出て、$c \log_a {y}= \log_b {y}$とわかる。ここで${y}=a$とすると、$c=\log_b a$である（この式は$a=b^c$からもわかるし、$c \log_a {y}= \log_b {y}$に${y}=a$を代入しても出てくる）から、

\begin{equation} \log_b a \log_a {y}= \log_b {y} \end{equation}

となり、

対数関数の底の変換

という公式を得る（最後の形では分母分子とも自然対数にしている）。

　なお、以上で使った計算で$a=b^c$の時$c=\log_b a$だったので、$b={\mathrm e}$を代入してできる式$a={\mathrm e}^{\log a}$をさらに${x}$乗して、

\begin{equation} a^{{x}}={\mathrm e}^{(\log a){x} } \end{equation}

という式を作ることができる。つまり全ての指数関数は（$2^{x}$だろうが、$1991^{{x}}$だろうが）適切な係数をつけた${\mathrm e}$を底とする指数関数（${\mathrm e}^{k{x}}$）の形で表現できることになる。実は${\mathrm e}^{なんとか}$の形の関数が一番扱いやすいことが後でわかるので、どんな指数関数でもこの形で考えられるというのは朗報なのである。

「指数関数（続き）」に戻る　「はじめに」に戻る。　「グラフの傾きを知る方法」へ

グラフの傾きを知る方法

関数の局所的ふるまいを知る

　関数を考える時、「ある点の近所での様子」だけを知ればよい、ということがある。この「近所の様子」を「局所的なふるまい」と呼ぼう。逆に全体を見てわかるのが「大局的ふるまい」である。局所的なふるまいを知るには、「その点での値」と「その点での傾き（正確には背線の傾き）」を知れば十分な場合がある。この章で考える微分という計算は「傾き」を知るという目標のためにある。

傾きしかわからないのでは知るべき情報が足りないのではないか？

と思うかもしれない一方で「局所的なふるまい」という情報を取り出すことで、全体を俯瞰していたのではわからないことに気づくことだってある。}。それはもちろんのことであるが、実は我々は「大局的なふるまいから局所的なふるまいを知る方法」、逆に「局所的なふるまいから大局的ふるまいを知る方法」、その両方を持っている。ここではまず前者の方を考えよう、というわけである。

　この方法は万能というわけではないが、ありがたいことに自然法則というのは局所的な法則になっていることが多い。少なくともこれまでの科学の歴史においてはまず局所的ふるまいを知り、それから大局的法則を出す、という筋道で理論を組み立てて結果として成功したこと（ニュートン力学がまさにこれ）が多い。だからこそ、局所的なふるまいを計算する方法である微分が自然科学において重要な役割をになうことになる。

ここまででも、多項式関数

y=a_nxⁿ+a_n-1x^n-1+… +a₃x³+a₂x²+a₁x+a₀

を考えた時、a₀が原点での値、a₁が原点での傾きであること（さらに$a_2$は原点での曲がり具合を表すこと）を説明してきた。x=0の近所だけを考えるなら、a₀とa₁がわかればよい、という考え方もできるわけである。

では、x=1付近を考えるときにはどうしよう。その場合、同じ関数を

y=b_n(x-1)ⁿ+b_n-1(x-1)^n-1+… +b₃(x-1)³+b₂(x²-1)+b₁(x-1)+b₀

のように書きなおす。これはちょっと頑張って計算すればできる。結果として、係数$a_i$と係数$b_i$はもちろん違う数になる実は$a_n$と$b_n$だけは常に同じである。なぜか、というのはこの式の中に含まれているxⁿの項を比較してみればわかる。。

　3次多項式関数を例として考えよう。

y=x³-3x²-x+3

という関数のグラフは右のとおりである。原点付近での局所的なふるまいは、（xが小さいところだから3次と2次の項を無視することにして）0次の項（定数項）と1次の項だけを残したy=-x+3で表される線（x=0における接線）を考えればよい（図にも描き込んである）。

　グラフには、x=1付近での「局所的ふるまい」を表す線（x=1における接線）も描き込んである。この線を知るにはどうすればよいかというと、この場合「小さい」と判断できるのはx-1だから、上の式をx-1の式に直す。ちょっと計算すると、

x³-3x²-x+3=(x-1)³-4(x-1)

が出せるので、こうしておいてx-1の高次の項を無視することにより、x=1での接線の式はy=-4(x-1)であることがわかる（グラフにはx=1の点ほか、いくつかの接線も描いてある）。

　まとめると、

\begin{equation} {y}=\underbrace{{x}^3-3{x}^2}_{{x}=0付近では\atop 無視できる部分} -{x}+3 =\underbrace{({x}-1)^3}_{{x}=1付近では\atop 無視できる部分}-4({x}-1) \end{equation}

のように一つの式を書き換えて、接線を求めている。

　このように「x=aという点での接線の傾きを知りたければ、x-aの式に書き直して…」ということをやれば任意の場所での接線の傾きを求められそうだが、この計算は「傾きを知りたい」という目標からすると少々計算が面倒すぎる---もっと簡便に傾きを知る方法がありそうである。

　というわけで、各点各点における接線の傾きを求める計算方法を以下で作っていくわけであるが、図からもある程度はどんな「接線の傾きを表現する関数」がどんなものになるかはわかる。上のグラフに「傾きのグラフ」を下に追加したのが右の図である。

　この図は、「グラフに接線を引いてみてその傾きを記録し、それを下のグラフにプロットする」という作業を地道にやっていけば描くことはできる。

　薄く塗った領域は傾きが負になっているところで、その領域ではyが右下がり、すなわち減少する関数になっている。この傾き（記号の意味は後で説明するが、とりあえずy'と書いた）はy'=3x²-6x-1という関数である。これをさっと計算する方法を知りたい、というのが「微分」を考える理由であるもし考えるべきなのが多項式だけなら、適当に変形してから0次と1次の項だけを取り出せばよいことになるが、そうでない一般の関数において通用する方法を考えたいのである。。

　では、次のページとその次のページで多項式と三角関数の場合の「傾きのグラフ」を動画で見よう。

「対数関数」に戻る　「はじめに」に戻る。　「多項式関数の傾き」へ

多項式関数の傾き

---

---

　上にあるのは３次関数のグラフで、関数の形とどこで接線を引くかを変更できるので、いろいろと変えて見ながら下のグラフが上のグラフの傾きになっていることを実感しよう。

「対数関数」に戻る　「はじめに」に戻る。　「三角関数の傾き」へ

三角関数の傾き

　同様に、三角関数の場合も傾きの関数を作ってみよう。

---

---

　こういう「傾きのグラフ」あるいは「傾きの関数」をどうやって求めていけばよいのか？？---という計算の部分は、来週からやる。

「多項式関数の傾き」に戻る　「はじめに」に戻る。　受講者の感想・コメントへ

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

「三角関数の傾き」へ　「はじめに」に戻る。