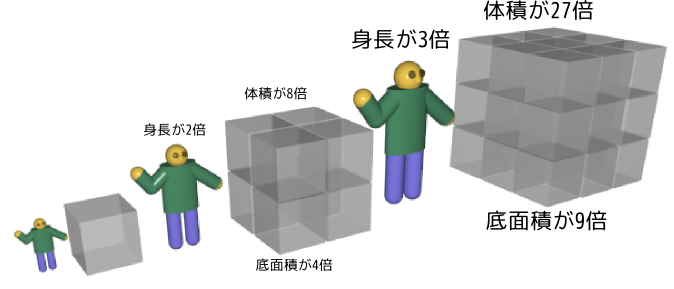
高階微分

導関数の導関数

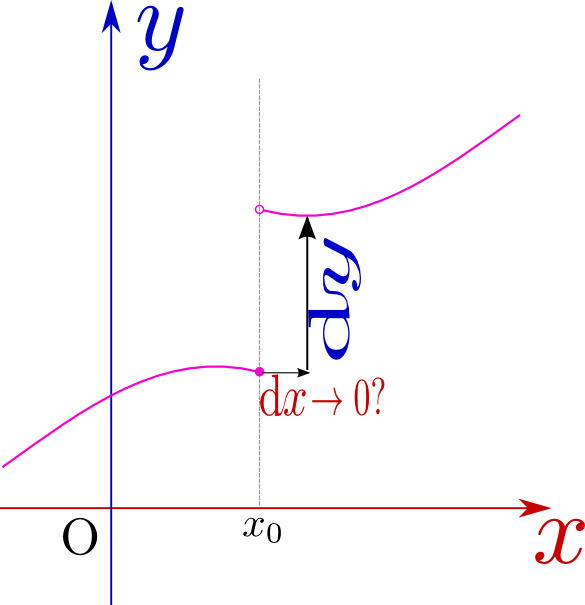
導関数$f'({x})=\lim_{{\Delta x}\to0}{f({x}+{\Delta x})-f({x})\over {\Delta x}}$の導関数、つまり

\begin{equation} f''({x})=\lim_{{\Delta x}\to0}{f'({x}+{\Delta x})-f'({x})\over {\Delta x}} \end{equation}

を作ってみよう。これを「二階微分」非常に頻繁に「二回微分」と書く人がいるが、これは誤字である（しかし発音では区別がつかないから安心だ）。と呼び、記号としては$'$を重ねて$f''({x})$と表現することにしよう（$f({x})\to f'({x})$が「一階微分」、$f({x})\to f'({x})\to f''({x})$が「二階微分」である）。また、一階微分を${\mathrm d \over \mathrm dx }f({x})$と書いたように、二階微分は

\begin{equation} f''({x})= {\mathrm d \over \mathrm dx }\left( {\mathrm d \over \mathrm dx }f({x}) \right)= {\mathrm d ^2\over \mathrm dx ^2} f({x})={\mathrm d^2 f\over \mathrm dx ^2}({x})\label{nikai} \end{equation}

と表現してもよい。

同様に三階微分や四階微分も定義されるが、数が大きくなった時は（十階微分を$f^{\prime\prime\prime\prime\prime\prime\prime\prime\prime\prime}({x})$などと書くのは不経済なので）$n$階微分は$f^{(n)}({x})$と表現する$\left(f''({x})={\mathrm d ^2\over \mathrm dx ^2}f({x})=f^{(2)}({x})\right)$。

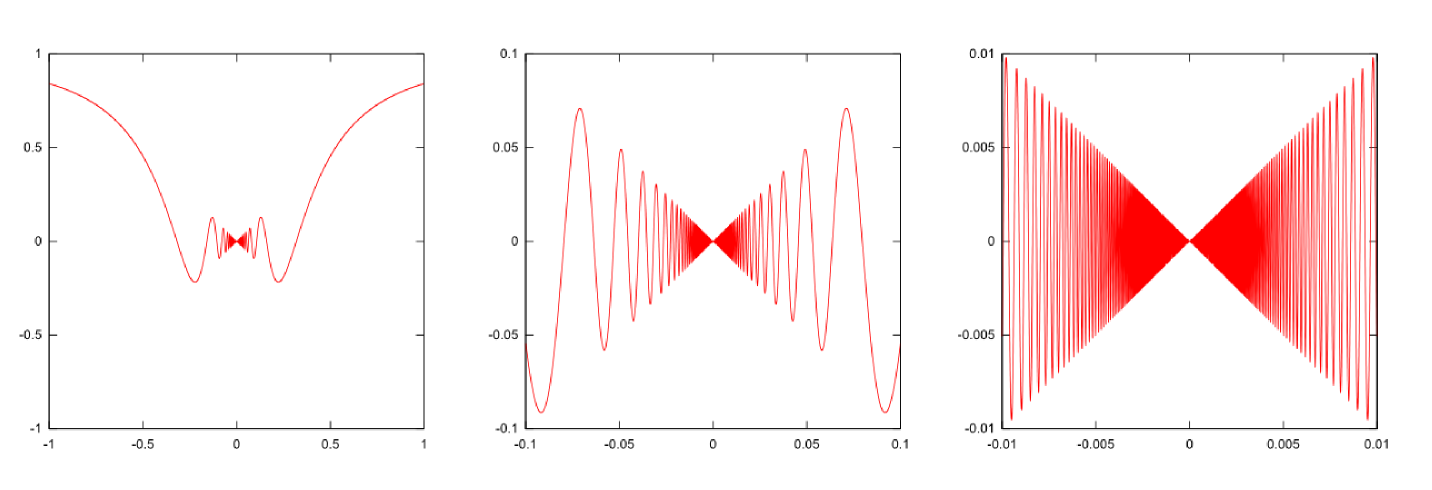
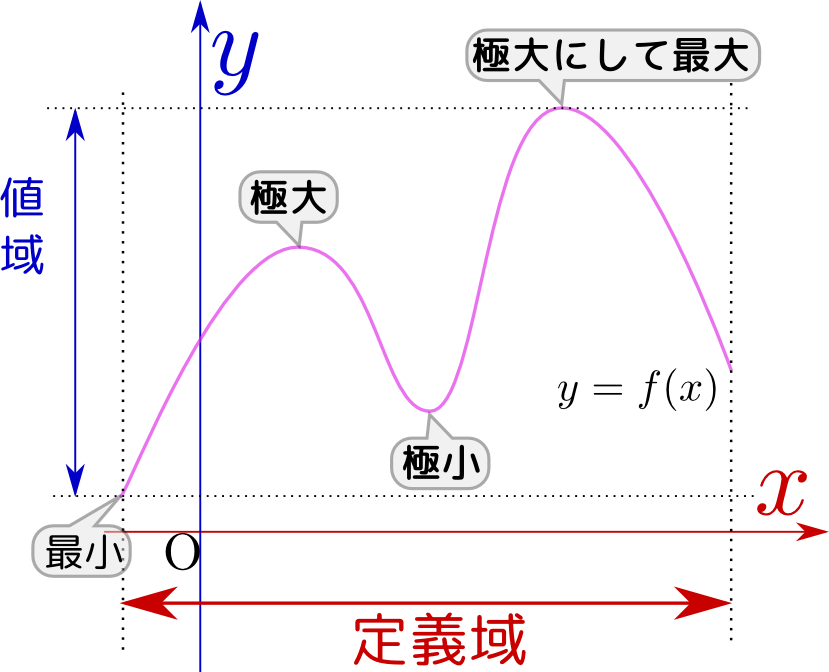
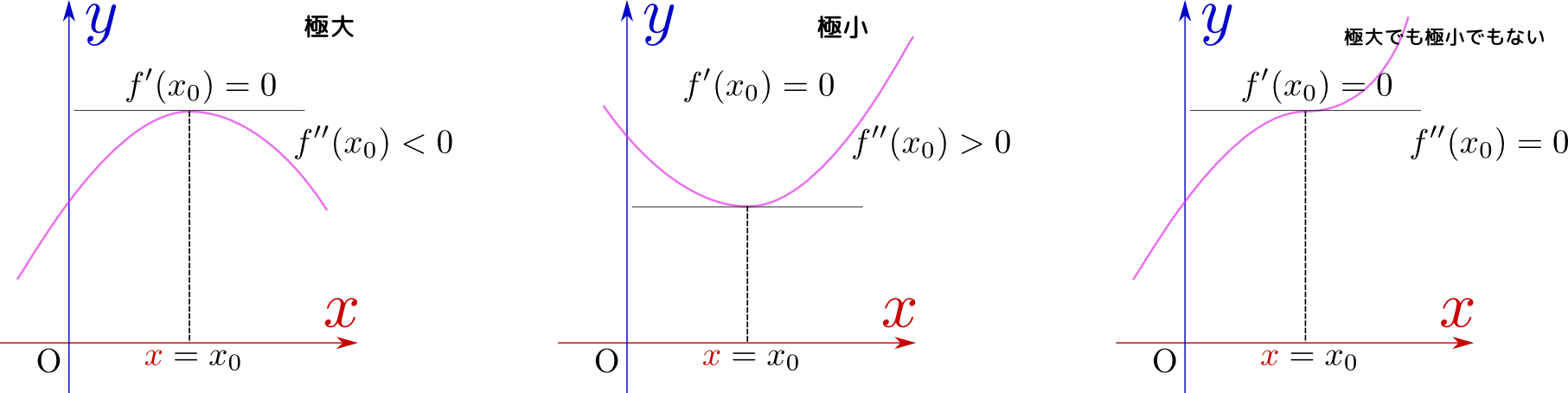
二階微分がどんな意味を持つかを考えよう。二次関数や三次関数の形を考えたときに、1次の項${x}$の係数が原点における傾きを、2次の項${x}^2$の係数が原点における「曲がり具合」を表現していたのを覚えているだろうか。その考え方からすると、二階微分の値は「曲線の曲がり具合」を表現することになる。

定義式から二階微分を計算することで、確かに「曲がり具合」であることを確認しよう。まず、$ f''({x})=\lim_{{\Delta x}\to0}{f'({x}+{\Delta x})-f'({x})\over {\Delta x}}$という二階微分の意味を表した式そのものに、一階微分の式$\lim_{{\Delta x}\to0}{f({x}+{\Delta x})-f({x})\over {\Delta x}}$を代入する。

\begin{equation} \begin{array}{rll} f''({x}) =&\lim_{{\Delta x}\to0}{\overbrace{ {f({x}+{\Delta x}+{\Delta x})-f({x}+{\Delta x})\over {\Delta x}}}^{f'({x}+{\Delta x})に対応} -\overbrace{{f({x}+{\Delta x})-f({x})\over {\Delta x}}}^{f'({x})に対応} \over {\Delta x} } \\[3mm] =&\lim_{{\Delta x}\to0} {\left( f({x}+{\Delta x}+{\Delta x})-f({x}+{\Delta x})\right) -\left( f({x}+{\Delta x})-f({x})\right) \over {\Delta x}{\Delta x} } \end{array} \end{equation}

という式が出る。

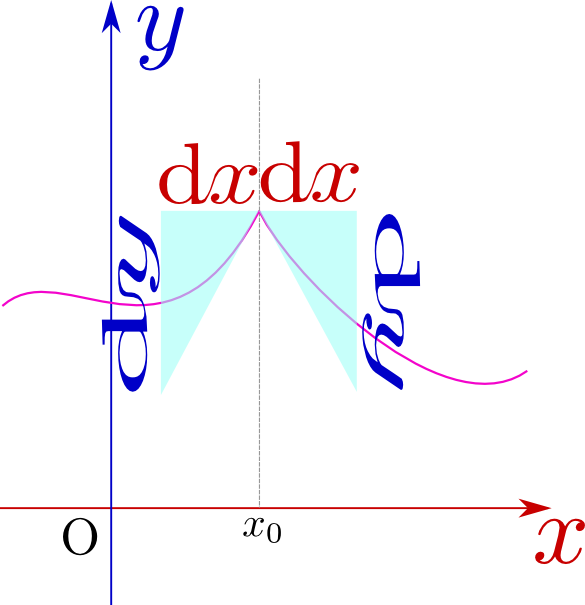
\begin{equation} \begin{array}{rll} f''({x}) =&\lim_{{\Delta x}\to0}{\left( f({x}+2{\Delta x})-f({x}+{\Delta x})\right) -\left( f({x}+{\Delta x})-f({x})\right) \over ({\Delta x})^2 } \\ =&\lim_{{\Delta x}\to0}{ f({x}+2{\Delta x})-2f({x}+{\Delta x}) +f({x}) \over ({\Delta x})^2 }\\ =&2\lim_{{\Delta x}\to0}{ { f({x}+2{\Delta x}) +f({x})\over 2} -f({x}+{\Delta x}) \over ({\Delta x})^2 } \end{array}\label{nikaibibunteigi} \end{equation}

という計算になる。最後で2を前に出したのは、分子の${f({x}+2{\Delta x})+f({x})\over 2}-f({x}+{\Delta x})$に図形的意味があるからである。

その意味するところを説明しよう。下のグラフを見て欲しい。

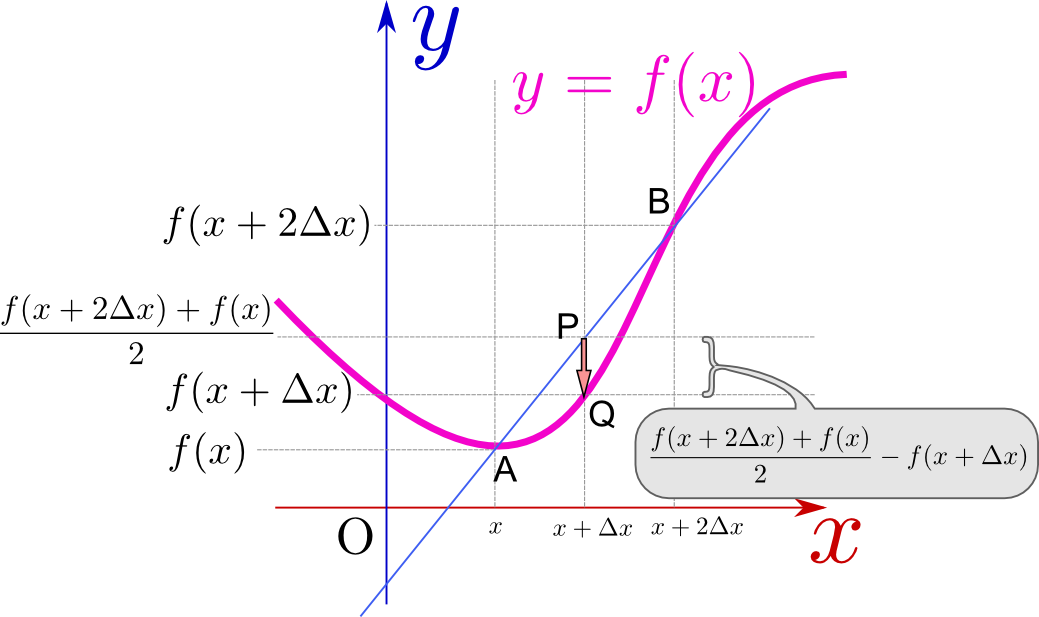
図の点Pは点A$({x},f({x}))$と点B$({x}+2{\Delta x},f({x}+2{\Delta x}))$の中点であり、その高さが${f({x}+2{\Delta x})+f({x})\over 2}$である。

一方$f({x}+{\Delta x})$は点Qの高さである。つまり、点Aと点Bの中点に比べて、点Qがどれだけ下がっているか、という量であり、これは「線の曲がり具合」を表現している。二階微分の値は「両隣の平均に比べて自分がどれだけ下がっているか」を示す量だとも言える。

それは上の図に示したように「上に凸か下に凸か」を表す量にもなっている。

　自然において、二階微分が正なら増加し、二階微分が負なら減るという傾向を持つ現象がたくさんある（後で、微分方程式でこれを表現するとどうなるか、ということを示そう）。これはつまり、下に凸なら増加、上に凸なら減少であり、すなわち平坦に戻そうという傾向のある現象なのである（たとえば水面・温度分布・濃度分布などにこういう傾向がある）。

　実のところ、自然法則の多くには二階微分までしか現れない。よって二階微分までをきっちりと理解していけば、自然法則のほとんどが理解できることになる。

微分に関する注意

微分に関するいくつかの注意

微分できない関数

微分ができない関数の例をいくつかあげよう。

　まずすぐにわかるのは連続でない関数で、この場合不連続な点（右の図の${x}=x_0$）で極限を取ると${\Delta x}\to0$にしても${\Delta y}\to0$にならないから、$\lim_{{\Delta x}\to0}{{\Delta y}\over {\Delta x}}$という式に意味がなくなる。「連続」という言葉の定義は厳密にしなければいけないところであるが、ここでは直観的な「グラフがつながっている」ということで理解しておこう。

このような関数の例は、前に出た階段関数$\theta({x})$や符号関数$\epsilon({x})$などがある。

たとえば${y}={1\over {x}}$で${x}=0$の時は値がない（定義されてない）上、${x}>0$の範囲で${x}=0$に近づくと$+\infty$へ、${x}<0$の範囲で${x}=0$に近づくと$-\infty$に近づく（これを数式では、$\lim_{{x}\to +0}{1\over {x}}=\infty,\lim_{{x}\to -0}{1\over {x}}=-\infty$と表現することもある）という状況で、極限での値も違う（$\tan{\theta}$の${\theta}={\pi\over 2}+n\pi$（$n$は整数）なども同様の意味で微分不可能である）。

また、たとえ連続でも「とがっている」つまり傾きが連続に変化してない場合、その点での微分は定義できない。

上の図のような場合、${x}=x_0$の左側（${x} < x_0$）で考えた微係数（接線の傾き）は正の値を取り、${x}=x_0$の右側（${x}>x_0$）で考えた微係数（接線の傾き）は負の値を取る。つまり同じ点に対して二つの傾きが計算できてしまうので、微分不可能になる。

　このような例で有名なのは、絶対値記号を含む関数${y}=|{x}|$などである。

自然現象を考えている時はこのような「つながってない（連続でない）」点や「とがっている（一階微分が連続でない）」点が出てくることは少ないので、多くの場合は「安心して微分してよい」ということになる（ただ、そうでない場合も有り得るのだと心に留めておいた方がよい）。

下は、$\sin{1\over {x}}$のグラフである（左から順に、範囲が$-1<{x}<1,-0.1<{x}<0.1,-0.01<{x}<0.01$と狭くなっている）。

この関数は無限大に発散することはない（$-1\leq \sin {\theta}\leq 1$だから）が、${x}=0$での値は全くわからないし、原点付近では${\Delta x}\to0$にしていくと振動がどんどん激しくなっていく$\sin {\theta}$の${\theta}$が$\infty$になっていく、と考えれば「これはえらいこっちゃ」と実感できるだろう。}ので${x}=0$では微分することもできない。

さらに、これに${x}$を掛けた$f({x})={x}\sin{1\over {x}}$という関数を考えてみよう。この関数も$f(0)$をそのまま計算しようとすると$\sin{1\over 0}$が出てきて困ってしまうのだが、幸い${x}=0$の極限での値はちゃんとある$\left(\lim_{{x}\to0}{x}\sin{1\over {x}}=0\right)$ので真面目にやるなら、$-1\leq \sin{x}\leq 1$より、$-|{x}|\leq{x}\sin{1\over{x}}\leq |{x}|$としてから極限を取ってはさみうちにする。、$f(0)=0$としておくと連続な関数になる。グラフは以下のようになる。

では微分はどうかというと、

\begin{equation} {\mathrm d \over \mathrm dx}\left({x}\sin{1\over {x}}\right)=\sin{1\over {x}}+{x}\times \left(-{1\over {x}^2}\right)\cos{1\over {x}}=\sin{1\over {x}}-{1\over {x}}\cos{1\over {x}} \end{equation}

となるが、この式は${x}=0$においては意味のない式になっている（第1項は$-1$から1までどんな値かわからないし、第2項も分母に${x}$がある）し、さっき定義した$f(0)=0$を使っても、やっぱり微分は定義できない。この関数は連続であるにもかかわらず微分不可能になっている。

陰関数の微分

関数というとここまでは${y}=f({x})$のように「従属変数が左辺に、独立変数が右辺に」とまとまった形で書いてきたが、そう書けない場合もある。このような関数の表示の仕方を「陰関数」と呼ぶ（「陰関数として表示する」のように使う）。この「陰」は「陽」の反対で、${y}=f({x})$の形は「陽に書けている」と言う。

陰関数の形でしか書けていない関数も、微分することはできる（ここまででも似たような計算はやっているので、それほど不思議には思わないだろう）。

という問題を考えよう。これを見て、微分${\mathrm dy\over \mathrm dx}$を計算するために${y}=\pm\sqrt{1-{x}^2}$の形にして微分する、ということをしたくなる人も多いかと思うが、これはかえってややこしくなる。

　この式の場合も、${x}^2+{y}^2=1$のまま微分した方が計算が楽である。

\begin{equation} \begin{array}{rll} {x}^2+{y}^2 &=1 &\\ 2{x}{\mathrm d}x + 2{y}{\mathrm d}y&=0&\\ {{\mathrm d}y\over {\mathrm d}x}=-{{x}\over {y}} \end{array} \end{equation}

こういう微分のやり方も慣れておくと便利である。

　こうして、$x^2+y^2=1$から${\mathrm dy\over \mathrm dx}=-{x\over y}$が出てきたわけですが、しばらくするとこの逆をやります。

高階微分 微分と極大・極小

微分と極大・極小

微分のもう一つの使い途は「極大値や極小値がどこであるかを求める」ことにある。

極大・極小

「極大(maximal)」と「極小(minimal)」は「最大・最小」に似た言葉である。違いは「最大・最小」は関数の定義域全体において最も大きい（あるいは小さい）値を取る場合を意味するが、「極大・極小」は定義域全体ではなく、今考えている「ある点」の近傍「ある点の近傍」はその点を内部に含むような領域のこと。においてのみ最も大きい（あるいは小さい）値をとっていればよい「極大」「極小」はつまり「局所的最大」「局所的最小」である。英語でそれぞれ「local maximum」「local minimum」と呼ぶこともある。。図に簡単な例で極大・極小となっている点と、考えている定義域内で最大・最小である点を示した図で「最小」とのみマークした点（定義域の下限になっている）はその点が考えている領域の端点であって領域の内部にはないから、最小にはなっているが「極小」ではない。。極大または極小である状況でかつ関数がその点で微分可能であるならば、その点では一階微分$f'({x})$が0になっていなくてはいけない微分不可能な、「尖った」点が極大・極小になっていることもあり得る。。

連続で、しかも少なくとも二階微分可能であるような関数を考える。この関数$f({x})$がある点${x}=x_0$において一階微分が0になった（$f'({x})=0$）とする。

もしこの点で二階微分が正（上図の左側）ならば、この場合この点では極大である。逆に負（上図の中央）ならば、この点では極小である。

二階微分が0である場合二階微分が0であり、かつその点の前後で二階微分が符号を変える場合、その点を「変曲点」と呼ぶ。変曲点は極大・極小とはまた別の概念である。は、極小である場合と極大である場合とどちらでもない場合があり得る（上図の右側ではどちらでもない場合のみを描いている）二階微分が0で極小である例としては${y}={x}^n$（$n>2$）kの${x}=0$がある。。

等周問題

辺の長さの和が同じ長方形の中で、もっとも面積が大きいのはどんな形だろう？---このような問題を「等周問題」と言う。これのもっとも簡単な問題である「等しい周の長方形の中で一番面積が大きいものはなにか？」を微分を使って考えてみる。

長方形の辺の長さの和を$4L$とする（一辺が$L$の正方形ならちょうど周の長さは$4L$であり、図に示したように横が$0.9L$になったら、縦は$1.1L$にならなくてはいけない）。縦の長さを${x}$とすると、横の長さは$2L-{x}$となる。面積は$S={x}(2L-{x})$となる。${x}$は$0<{x}<2L$の範囲で意味があるから、それを定義域としてグラフを描いてみると右のようにになる（もちろん、グラフを描かなくても以下の話はわかる）。

微分を実行すると、

\begin{equation} {\mathrm dS\over \mathrm dx}= 2L - 2{x} \end{equation}

が0になるのは${x}=L$の時、つまり正方形の時である。

　一周の長さを計算すると、$2x+2{S\over x}$になる。これを$x$で微分すると$2-2{S\over x^2}$で、これが0になるのは$S=x^2$のとき。つまりは正方形になるときである。

スケール変化と最適なサイズ

物体のサイズを変えていったとき、いろんな量がサイズの関数として表現される。たとえば人間の身長を$h$とすると、体重はだいたい$h^3$に比例する（直方体で考えた時に体積が縦・横・高さの積で表されることを考えれば、まず体積が$h^3$に比例することはわかるだろう）。また、骨が支えることができる重さは面積に比例するだろうから、$h^2$に比例する。

そこで、身長を$h$として体重を$W=wh^3$と書き、その人の足が支えることができる重さを$B=bh^2$と書こう（つまり、これよりも足に掛かる力が強くなったら足の骨が折れる、とする）。すると、持つことができる荷物の重さは（自分の体重の分は引いておかなくてはいけないので）$S=B-W=bh^2-wh^3$となる。

ここで、体重は三乗に比例し、支えることのできる重さは二乗に比例し、と冪が違うこと、つまり「スケール変化による変数の変化の仕方に違いがあること」に注意しておこう。$h$が小さい領域では二乗と三乗では二乗の方が大きいが、$h$が大きい領域では逆転する。つまり、$h$があまり大きすぎると、足が支えられる体重よりも自分の体重の方が重い（立っていられない）という状況が出現するのである。自然現象の起こるスケールというのは、このように異なるスケール変化をする変数の間の「せめぎあい」で決まる。

実例として人間の身長が妥当なものかどうかを検討しよう。簡単の為、「標準人間」として「身長2 mで体重100 kg、200 kgの荷物を持って立つことができる人」（通常の３倍までの重力がかかったと仮定しても耐えられる人、と考えてもよい）を設定しよう。すると、$100=8w$より、$w=12.5$であり、$200=4b-100$より、$b=75$である。他の人間は全て標準人間のサイズ変化させたものだとしよう（もちろんこの仮定はむちゃくちゃであるが、「第一近似」としてよいことにしよう）。

標準人間および標準人間をスケール変化させた人間に対しては、持つことができる荷物の重さは$C=75h^2-12.5h^3$という式で書ける。これからすると、もっとも重い荷物が持てるのは、

\begin{equation} {\mathrm dC\over \mathrm dh}=150h-37.5h^2=0~~~より~~~h={150\over 37.5}=4 \end{equation}

で、$h=4$（身長4 m）の人である（下のグラフも参照せよ）。

つまり、どんどん巨大になれば持てる荷物も増えるのかというとそうではない。右でグラフで示したように、体重の増加（三乗比例）はいずれ支えることができる重さ（二乗比例）に勝ってしまう。だからある身長（$h=6$）より高いとそもそも立っていられない。そして、保持できる荷物の重さには最大値がある（それが$h$の最適値であるとも言える）。

実際二足歩行する動物のサイズがせいぜい2 mぐらいなのは、ここで行った計算がだいたい正しいことを示している（立って荷物を持つだけでなく、走ったりして動きまわらなくてはいけないのだから、ある程度余裕を持たせておかないといけないわけである）。

微分に関する注意 受講者の感想・コメント

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

微分と極大・極小