自然科学のための数学2015年度第18講

　まず、第16講でもやった「微分方程式を図解する」の最後のページで、いろんな微分方程式とその解の図を動かしながら遊んでもらった。

　ここで、

を実感してもらったところで、微分方程式の解の含むパラメータについての話に入った。

微分方程式の解に含まれるパラメータの数

　微分方程式の解には微分方程式だけでは決まらないパラメータが必ず含まれる。それは微分方程式が局所的情報を表す式であることからくる必然的性質である。微分方程式を解く時にもこの点は大事なので、そのパラメータの数について考察しておこう。${\mathrm dy\over \mathrm dx}={y}$の解が${y}=A\mathrm e^{{x}}$だったことを例として考えよう。

　パラメータ$A$は変数分離を行った結果の${\mathrm dy\over {y}}=\mathrm dx$を積分するときの積分定数から現れる。具体的な積分結果は$\log{y}={x}+C$であるが、$ {y}=\mathrm e^{{x}+C}=\mathrm e^C \mathrm e^{{x}}$となるから、$A=\mathrm e^C$である。

　次に二階微分方程式の簡単な例$\left({\mathrm d\over\mathrm dx}\right)^2f({x})={\mathrm d\over\mathrm dx} f({x})$を同様に解いてみよう。

\begin{equation} \begin{array}{rll} \left({\mathrm d\over\mathrm dx}\right)^2f({x})=&{\mathrm d\over\mathrm dx} f({x}) &{両辺を不定積分} \\[-2mm] {\mathrm d\over\mathrm dx} f({x})=&f({x})+C \end{array} \end{equation}

と、ここまでできたところで、この後どうする？と聞いてみた。

両辺を$f(x)$で割る。
そうすると、 $$ {{\mathrm d\over\mathrm dx} f({x})\over f(x)}=1+{C\over f({x})} $$ となっちゃって、最後の${C\over f({x})}$ですごく困る。
最初の式に代入して、 $$ \left({\mathrm d\over\mathrm dx}\right)^2f({x})=f({x})+C $$ にする。
ふむ。それは面白いけど、せっかく「二階微分方程式」→積分して→「一階微分方程式」としたのに、また二階微分方程式に戻ってしまうのは、ちょっと悲しい。

　こういうときは、まだわからない$f(x)$と、未定の$C$を「わからないものどうし」でまとめてしまうという手がある。すなわち、${y}=f({x})+C$と置く。

　すると、 \begin{equation} \begin{array}{rll} {\mathrm d\over\mathrm dx} (y-C)=& y&{{\mathrm d\over\mathrm dx}(-C)=0を使って、さらに変数分離}\\[-2mm] {\mathrm dy\over {y}}=& \mathrm dx&{もう一度積分}\\[-2mm] \log {y}=& {x}+D&{\mathrm e の肩に乗せて}\\[-2mm] {y}=&\mathrm e^{{x}+D} \end{array} \end{equation}

　こうして解は（$f({x})$に戻して）$f({x})=-C + \mathrm e^{{x}+D}$または$f({x})=-C+D'\mathrm e^{{x}}$（$D'=\mathrm e^D$）となり、積分を二度やった結果として積分定数$C,D$（または$C,D'$）の二つのパラメータが現れる。

微分方程式を解くとは積分すること、と考えると「$n$階微分方程式なら不定積分を$n$回繰り返せば解ける」と言えて、結果は$n$個の積分変数を含む。上の具体例を見ると、確かに一階微分方程式の解は1個の、二階微分方程式の解は2個の積分定数を含んでいる。

　結論として、$n$階微分方程式の解は常に$n$個の「微分方程式だけでは決まらないパラメータ」を含んでいるただし、途中で関数が定義できない点（たとえば${y}={1\over {x}}$の${x}=0$）があると積分一つに対して二個の積分定数が出て来ることもあるので、そのような場合には注意が必要である。。

　一階微分方程式で正規形の場合で、「決まらないパラメータ」の意味を考えておこう。

${\mathrm dy\over \mathrm dx}=f({x},{y})$は、${x}$-${y}$平面上である点$({x},{y})$を指定したとき、その点における関数のグラフの傾き${\mathrm dy\over \mathrm dx}$、すなわち各点各点において「グラフの線はどちらに伸ばすべきか」を与える式である。

　最初に考えた微分方程式${\mathrm dy\over \mathrm dx}={y}$の解の曲線は、各場所において${y}$座標と同じ傾きを持つ。解の曲線を次々と描いていくと、次のグラフにあるように全平面を埋め尽くす。

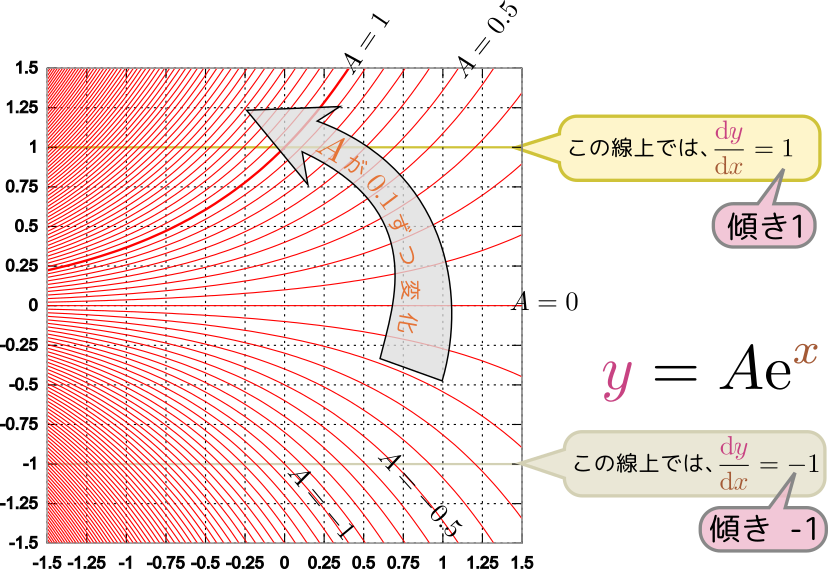
${x}=0$の時${y}=1$というふうに「出発点」を決めると、この場合は${y}=\mathrm e^{{x}}$という線（グラフでは１本だけ太い線で表現した）の上を進んでいく。

　一階微分方程式が指定するのは傾きのみであるから、出発点（上の例では${x}=0$から始めたが、実はどの場所でもよい）を指定すれば曲線は一つ決まる。別の点を出発点にすれば（たまたま同じ線上の２点を選ばない限り）また別の線が引ける。たとえば${x}=0$の時${y}=2$と決めたなら、${y}=2\mathrm e^{{x}}$の上を進む。こうして、微分方程式だけからは決まらないパラメータが解には入っている（後で、それを「初期条件」などで決めていく方法について述べる）。

先週の方程式の場合

先週の微分方程式の場合

　先週の微分方程式の場合で、「未定のパラメータ」が何を意味するものであったかを考えよう。

　ロケットの場合、 $$ m\mathrm dV = -w\mathrm dm $$ が微分方程式で、解は$V=-w\log m +C$だった。この場合積分定数$C$の違いは、初速度の違いである。

　流行の方程式 $$ {\mathrm dy\over \mathrm dt}=k{y}(1-{y}) $$ の解は $$ {y}={1\over 1-\mathrm e^{\pm k {t}-C}} $$ だが、この積分定数$C$はいわば「流行がいつスタートしたか」を表す数字だと思えばよい。

　さて、ちょっとここで問題を変えてみよう。

　あるものが流行るかどうかは何で決まるだろう？？先週は「周りに流行に乗っている人が多ければさらに流行に乗る人が増える」ということから「${\mathrm dy\over \mathrm dt}$は$y$に比例する」として、さらに「すでに流行に乗った人は関係ないから、${\mathrm dy\over \mathrm dt}$は$1-y$に比例する」と考えて、${\mathrm dy\over \mathrm dt}=k{y}(1-{y})$とした。

しかし実際に流行が起こるときに他に関係しそうなものはないだろうか？
CMとか？？
それはありそうだね。というわけでその問題を考えましょう。
今日の小テスト

流行を考えるが、今回は「周りの影響」ではなくCMの影響で流行が起こるとしよう。すると、「${\mathrm dy\over \mathrm dt}$は$y$に比例する」はなくなる。一方、「すでに流行に乗った人は関係ないから、${\mathrm dy\over \mathrm dt}$は$1-y$に比例する」はやはり成り立つ。微分方程式を立てて、解け。

　答えは以下の通り、$1-y$に比例するから、微分方程式は $$ {\mathrm dy\over \mathrm dt}=k(1-{y}) $$ （$k$は上の微分方程式とはまた別の変数）となる。これを解く。変数分離して、 $$ {\mathrm dy\over 1-y}=k\mathrm dt $$ 積分して、 $$ -\log(1-y)=kt+C $$ これから、 $$ 1-y=\mathrm e^{-kt-C} $$ となるので、 $$ y=1-\mathrm e^{-kt-C} $$ が解。

　何人かできたところで、「できた人は$y$がどんな変化をするか考えて、できればグラフを描いてみよう」と声を掛けた。というのは、積分でうっかりして符号を忘れて、

$$\log(1-y)=kt+C$$

としている間違いが多かったからである。

　この間違いをすると最終結果が

$$y=1-\mathrm e^{kt+C}$$

となってしまう。あるいは、

$$y=1+\mathrm e^{kt+C}$$

のように間違えていた人もいるが、この誤答では$t$が大きくなっても$y=1$に近づかない（どころか、$\pm\infty$に行ってしまう）。$y$が本来0から1までの数字であることを考えると有り得ない。

　ちなみに$C=0,k=1$の場合でグラフを描くと、

のようになる。これだと「時間がたつと$y=1$（100％）に近づく」ということがよくわかるだろう。

　微分方程式を解くときは、結果をある程度は予想し（←数式が解けなくても「こうなりそうだ」という予想は立つ）、計算結果が実際の状況に合致しているかどうかをチェックすることが常に必要である。

微分方程式の解に含まれるパラメータ 受講者の感想・コメント

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

日常的なことで、流行についての微分方程式などはある程度のグラフの形はイメージできるので、じっさいに解いて出た答えと照合することで、だいたいの正誤がわかる。これを利用してミスの少ない解き方を目指したい。
常にそういう考えをするようにしましょう。

わかりにくいものはひとまとめにするというのは便利だと思いました。
いろんな場面に適用してみてください。

小テストで$\int{1\over 1-y}\mathrm dy=-\log(1-y)$が混乱して$-\log(1-y)$をなぜか右辺にもマイナス１をかけてあげて計算した（←間違い）。Cmの場合は周りに関係なく見た人が買うかどうかの割合が問題なので、${\mathrm dy\over\mathrm dt}=k(1-y)$であることまでは式を立てることができた。
次は注意深く計算していきましょう。

二階微分を解いている途中で${\mathrm d\over\mathrm dx}g(x)=g(x)$が出てきて「？」となった。文字が違うだけでできる問題ができなくなったらもったいないと思うので、文字にまどわされず問題が解けるようになりたい。
文字の違いは全く本質的じゃないので、まどわすれないように。

微分方程式を立てるのが難しい。
じゃあどんどん練習しよう。

しっかり復習してがんばろうと思いました。
がんばってください。

$\int{\mathrm dy\over 1-y}=-\log|1-y|$で負の符号がつくことを忘れていた。$y=1-\mathrm e^{-kt+C}$になるのはイメージ出来たが、途中の計算が間違っていたため、スタートで負の符号をつけてしまった。
そういうときはやはり、丁寧に見なおさないと。

自分で微分方程式を立てることができたが、計算の時に符号間違いと積分定数を付け忘れてしまった。
積分定数は今日のメインテーマだから、忘れては困るなぁ。

微分方程式を立てるとき、なかなか思いつくのが難しい。
起こっている現象を素直に数式に移していくだけです。「思いつき」なんていらない。

小テストの答えが合っていたので良かったです。でもグラフが描けなかったので検算（？）ができなかった。
グラフが書けないときは、せめて「$t$が大きいとどうなるか？」などを考えてみましょう。

流行の方程式って本当にあたっているんですか？
状況によりますが、あたるときはあたります。現実に合うようにいろんなモデルを考えていく。

身の回りの現象をもっと微分方程式で解いてみたいと思った。
やってみましょう。

小テストの問題を通して多少の成長を実感できた。
少しずつでも、成長していこう。

復習を含めながら授業が進んでいったためついていけなくなることがなくてよかった。今日の小テストのレベルもちょうどよく、あと２，３問、問題を出されても楽しかったと思う。
あとは自分でいろいろ考えてみてください。

自分で実際に微分方程式を作り出すというのはとても大変だった。微分方程式を立てる時の工夫する点なども学べた。
微分方程式は立てるところも解くところも大事で、面白いものです。

小テストをやったが、微分方程式を立てるところからミスってしまった。方程式を立てる際の現象をもっと考え理解していくようにしたい。
現象と数式を結びつけて考えていくことが大事です。

最後の微分方程式の問題を解いたとき、∞に発散する答えを導いてしまった。符号ミスやちょっとした計算ミスで、実際には有り得ない現象を導いてしまうのだなとわかった。
人間はミスをするものなので、チェックをしながら進めていくことが大事です。

変数分離以外の方法でも、解けるようにしたい。
次回からもいろいろやっていきます。

マイナスをつけるの忘れていた。人口超える。
次はチェックしながら計算しましょう。

しっかり微分方程式を解けるようにしていきたい。
どんどん解いていきましょう。

$-y$なのに積分をして$-$を付け忘れた。微分をしたときはなかなか忘れないので、積分の演習をしっかりやってこの場合でいう$y$の係数を注意することを習慣づけようと思った。
注意しつつ、勉強していきましょう。

ある程度こんな値になるなという予想を立ててからやることが大切だとわかった。
今後気をつけてやってみてください。

実際にCMの流行を解いてみてほんとうに楽しかったです。でも積分を間違っては元も子もないのでもっと演習して積分の力をつけたいと思います。
こういうのは訓練が一番です。

積分すると一階ごとにパラメータが一つずつ増える。計算のあとはそのことがらを考えておかしいところがないか確認する。
確認は、常に注意しましょう。

微分方程式の基本的な計算ついて、変数分離をする式変形によって積分が計算できることがわかった。
変数分離は微分方程式の基本なので、習得しておきましょう。

演習問題が難しかった。微分←→積分という確認の習慣をつけたい。
今日はまだ基本です。頑張っていこう。

流行ってこうやって数式で表せるんだなぁって思いました！　微分方程式ってすごい！　積分も
いろいろ役立ちます。

自分でもその他の現象について微分方程式を立て、現象の様子を確認したい。
どんどん、やってください。

微分方程式の立て方が少しだけわかった。$\left({\mathrm d\over \mathrm dx}\right)^2f(x)=f(x)+C$の解き方はどうなるんでしょうか？　また、微分をたてるとき、${\mathrm dy\over\mathrm dx}=$？の右辺をyの関数で書けばよいのかxの関数で書けばよいのかわからない。
この後いろんな解き方を習うとできるようになります。なお、右辺をxで書くかyで書くかなんて悩む必要はありません。どっちでも書けるという状況はないからです（そうなってたら、もう微分方程式は解けている）。

符号ミスをしていた。流行などの問題では、普通に考えてわかることは判断できるようにしたい。
常に「現実と合っているかな」とチェックするようにしましょう。

最後の小テストで、自分で微分方程式を立てるということができませんでした。先生の説明あってわかりました。そういうこともできるようにしたいです。
練習していきましょう。

今日の小テストで、自分の発散するという答えが間違っていることはわかったのですが何が間違っているのか見つけられず結局間違ってしまいました。logの積分には以後気をつけます。
logにかぎらず気をつけていきましょう。

現象に見合った解をみつけなければなりませんね。
正しく計算すれば現象に見合った解が出てくるはずなのです。

微分方程式で何なのかわかるようになってきてます。まだ簡単な微分方程式を解いていると思うけど、基礎をしっかり身につけて応用問題にも対応できるようにしておきます。小テストは最後解き終わって自分が間違っていることに気づいて直すことができたので、一安心です。
しっかり練習して身につけていってください。

何階微分かで未定のパラメータも変わるとわかった。テストで積分の計算を間違えてしまったので、理解が足りないと思った。
練習しよう。

流行の微分方程式を立てることができたのですが、イメージができなかった。グラフが描けなかった。計算を間違えたけど説明を聞いて納得できたので、次はミスらないようにする。
では、次はがんばりましょう。イメージすることは大事です。

今日のCMの流行方程式を自分で作ることは全然ダメ。$ky(1-y)$の部分を変えると知るけど、目線はずっと$(1-y)$の方にいて、違いました。
$(1-y)$は「すでに流行に乗っている人は影響を受けない」という部分なので、CMがあってもなくても同じ形になる、ということに気づいてください。

流行を考えるときに何が影響するかによって全然答えが違ってくることがわかった。また、出てきた答に対して実際の事象を当てはめて考えてみて、間違いをなくせるようにしたい。
答えがいろいろ出るからこそ現実に合わせることもできるのです。現実を考えるときはもっと複雑な方程式が必要になることもあります。

僕はCMが入るといらいらするので、逆に買いたくなくなります。
ではそういう人は方程式にどんなふうに入れればいいのか？　考えてみてください。

${\mathrm dy\over 1-y}$の積分がまちがっていた。もっと問題の状況を考えながら問題を解くようにする。
いろいろ問題を解いてみてください。

今日の小テストで式をヒントなしではできなかったので、考える力をつけたい。
じっくり、練習をしましょう。

流行は簡単な式で表せるのですね。
今やっているのは現実よりかなりシンプルにしたモデルです。

「CMで流行がはやる場合」という「流行がはやる」という元も子もない言葉は大好きです。
馬から落馬したり頭痛が痛かったり。

小テストで${1\over 1-y}$の積分を一回間違えそうになって危なかったです。まだまだ精進が必要だと感じました。
では、問題演習をどんどんやって精進してください。

CMを見て流行がはやる場合、どのように時間経過するのかをまず予想することが大切であると思った。
それはこの場合だけでなく、いつでもです。

先週の微分方程式の場合