自然科学のための数学2015年度第19講

　第16講でもやった「微分方程式を図解する」の最後のページには、${\mathrm dy\over\mathrm dx}=y+x$という微分方程式がある。これの解は下の図のようである。

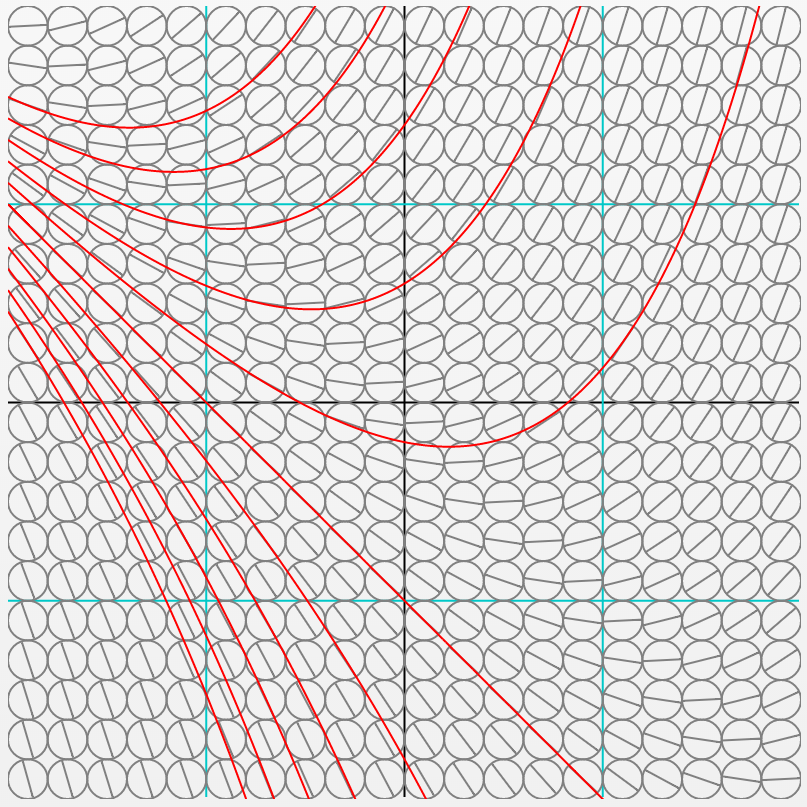
　この微分方程式、変数分離では解けない（変数分離できないから）。

　そこで変数分離以外の「微分方程式を解くテクニック」が必要となってくる。次に考えるのは微分方程式が「線形微分方程式」である場合である。

というわけで、今日の授業の目標は微分方程式${\mathrm dy\over\mathrm dx}=y+x$を解く方法を考える！である。実はこれは「線形微分方程式」の一例である。

線形微分方程式とは

　「線形」というと難しげだが、意味は『グラフで描いたら直線』（線形は英語ではlinear）、あるいは『数式で表すと1次式』という意味である。たとえば$ay+b$は$y$に関し線形。そうでない${1\over y},y^2,\sin y$などは「非線形」となる。

　線形微分方程式というのはたくさんある微分方程式の中で特に簡単なものを考えていることになるが、幸い自然現象ではこの簡単な例になっているものが結構ある（たとえば音や光の波動方程式は線形だと言ってよい）。

　というわけでここからしばらく線形微分方程式を考えていく。そのために必要な言葉から整理していこう。

線形結合

　線形微分方程式を解くときに助けとなる「重ねあわせの原理」に関連してこの後使うので、「線形結合(linear combination)」という用語を説明しよう

線形結合
${x},{y},\cdots$という複数個の量がある時、適当な定数$a,b,\cdots$を掛けて足した$a{x}+b{y}+\cdots$のことを、「${x},{y},\cdots$の線形結合」と呼ぶ。

　単純に言えば「○○の線形結合」とは「変数の組○○から、定数倍と足算によって作られる量」になる$-1$倍して足すという計算も含まれるので、引算も含まれていることに注意。。${x}$と${y}$を掛けたり割ったりしてはいけない（自乗もダメ）。

線形斉次微分方程式の解の重ねあわせ

　線形斉次微分方程式（ここで、$A_n({x}),A_{n-1}({x}),\cdots, A_0({x})$は${x}$のみの関数である） \begin{equation} \left( A_n({x})\left({\mathrm d\over\mathrm dx}\right)^n +A_{n-1}({x})\left({\mathrm d\over\mathrm dx}\right)^{n-1} +\cdots +A_{1}({x}){{\mathrm d\over\mathrm dx}} +A_0({x}) \right){y} =0\label{senkeiseiji} \end{equation} の解をいくつか（${y}=y_1({x}),{y}=y_2({x}),\cdots$としよう）見つけたならば、それらの線形結合である${y}=a_1 y_1({x})+a_2 y_2({x})+\cdots$も解である。

　このように「（線形斉次微分方程式の場合）解の線形結合がやはり解であること」を「重ねあわせの原理」と呼ぶ。証明は簡単で、二つの式 \begin{eqnarray} \left( A_n({x})\left({\mathrm d\over\mathrm dx}\right)^n +A_{n-1}({x})\left({\mathrm d\over\mathrm dx}\right)^{n-1} +\cdots +A_{1}({x}){\mathrm d\over\mathrm dx} +A_0({x}) \right)y_1({x}) &=&0\\ \left( A_n({x})\left({\mathrm d\over\mathrm dx}\right)^n +A_{n-1}({x})\left({\mathrm d\over\mathrm dx}\right)^{n-1} +\cdots +A_{1}({x}){\mathrm d\over\mathrm dx} +A_0({x}) \right)y_2({x}) &=&0 \end{eqnarray} をそれぞれ$a_1$倍、$a_2$倍して足せば、以下のような求めるべき式ができる。 \begin{equation} \left( A_n({x})\left({\mathrm d\over\mathrm dx}\right)^n +A_{n-1}({x})\left({\mathrm d\over\mathrm dx}\right)^{n-1} +\cdots +A_{1}({x}){\mathrm d\over\mathrm dx} +A_0({x}) \right)(a_1 y_1({x})+a_2y_2({x}))=0 \end{equation} もちろんこれはこの微分方程式が線形斉次（${y}$の1次式しかない）だからこそ成り立つ。たとえば${\mathrm d\over\mathrm dx} {y}+{y}^2=0$という非線形微分方程式では、あきらかに重ねあわせはできない。 \begin{equation} \begin{array}{rlll} &{\mathrm d\over\mathrm dx} y_1({x})&+(y_1({x}))^2=&0 \\[3mm] + &{\mathrm d\over\mathrm dx} y_2({x})&+(y_2({x}))^2=&0 \\[3mm] \hline &{\mathrm d\over\mathrm dx} (y_1({x})+y_2({x}))&+(y_1({x}))^2+(y_2({x}))^2=&0 \end{array} \end{equation} となって、${\mathrm d\over\mathrm dx} {y}+{y}^2=0$に${y}=y_1({x})+y_2({x})$を代入した結果である \begin{equation} {\mathrm d\over\mathrm dx} (y_1({x})+y_2({x}))+(y_1({x})+y_2({x}))^2=0 \end{equation} とは違う式になる。

非斉次の場合の重ねあわせ

　非斉次の場合、つまり${y}$の1次のみではなく${y}$の0次の項がある線形微分方程式 \begin{equation} \left( A_n({x})\left({\mathrm d\over\mathrm dx}\right)^n +A_{n-1}({x})\left({\mathrm d\over\mathrm dx}\right)^{n-1} +\cdots +A_{1}({x}){\mathrm d\over\mathrm dx} +A_0({x}) \right){y} =C({x}) \end{equation} の解を考えてみる。右辺においた、線形非斉次微分方程式の0次の項$C({x})$（${y}$を含んではいけないが、${x}$の関数であってもよい）のことを「ソースターム(source term)」あるいは単に「源」または「ソース」と呼ぶ話し言葉では「ソース」と呼ぶことが多い。このように呼ぶ理由は、このような方程式が「$C({x})$という量が${y}({x})$を作り出す」という法則を表現することが多いからである。たとえば「ストーブがあるとまわりは温度が高い」「質量があるとまわりに重力場ができる」「電荷があるとまわりに電場ができる」などの場合「ストーブ」「質量」「電荷」が\ruby{源}{ソース}である（こういう現象も微分方程式で表現できるのだ）。。この式の応用として面白いのは、以下の事実である。

線形非斉次微分方程式の重ね合わせ
「$C_1({x})$を源とする解」と「$C_2({x})$を源とする解」の和は「$C_1({x})+C_2({x})$を源とする解」。

　これを数式で確認しておこう。 \begin{equation} \small\begin{array}{rlll} & \left( A_n({x})\left({\mathrm d\over\mathrm dx}\right)^n +\cdots +A_{1}({x}){\mathrm d\over\mathrm dx} +A_0({x}) \right)y_1({x}) &=C_1({x})\\ & \left( A_n({x})\left({\mathrm d\over\mathrm dx}\right)^n +\cdots +A_1({x}){\mathrm d\over\mathrm dx} +A_0({x}) \right)y_2({x}) &=C_2({x})\\[3mm] \hline & \left( A_n({x})\left({\mathrm d\over\mathrm dx}\right)^n +\cdots +A_{1}({x}){\mathrm d\over\mathrm dx} +A_0({x}) \right)(y_1({x})+y_2({x}))&=C_1({x})+C_2({x})\\ \end{array} \end{equation} となる「$C_1({x})$を源とする解」と「$C_2({x})$を源とする解」の線形結合の場合に拡張すれば、「$\alpha_1 C_1({x})+\alpha_2 C_2({x})$を源とする解」を作ることもできる。上の場合、$\alpha_1=\alpha_2=1$の場合である。$\alpha_1=1,\alpha_2=-1$にすれば「差」になる。。

　最初に言ったように、線形微分方程式は様々な現象に現れるが、結果としてこの世界で起こる現象の多くは重ね合わせの原理を満たす。たとえば音を表す微分方程式は線形で、重ね合わせの原理が使える。これは何を意味するかというと「A君がだまっていてB君が話したときの音」と「B君がだまっていてA君が話したときの音」を単純に「足し算」すれば「A君とB君が同時にしゃべっているときの音」になるということ。これが満たされてないと、「あっちからA君が『お〜い』と呼んだ声とB君が『やっほー』と呼びかけた声が空中ですれちがって互いにちゃんと聞こえる」のような現象も起こらなくなる。

　次のようなことも言える。

非斉次方程式 \begin{equation} \left( A_n({x})\left({\mathrm d\over\mathrm dx}\right)^n +A_{n-1}({x})\left({\mathrm d\over\mathrm dx}\right)^{n-1} +\cdots +A_{1}({x}){\mathrm d\over\mathrm dx} +A_0({x}) \right){y}=C({x}) \end{equation} と、上の式で$C({x})=0$とした斉次方程式 \begin{equation} \left( A_n({x})\left({\mathrm d\over\mathrm dx}\right)^n +A_{n-1}({x})\left({\mathrm d\over\mathrm dx}\right)^{n-1} +\cdots +A_{1}({x}){\mathrm d\over\mathrm dx} +A_0({x}) \right){y} =0 \end{equation} を考える。非斉次方程式の解として$y_1({x})$を１つ、斉次方程式の解として$y_0({x})$を１つ、それぞれ見つけたとする。${y_0}({x})+y_1({x})$もまた、\強調{非}斉次方程式\式{hiseijirei}の解である。

　これは上で考えたことの$C_2({x})=0$の場合にあたるから、証明は不要だろう。わざわざこんな（言わば、「あたりまえ」の）ことをここに書いたのは、この事実は応用範囲が広いからである。というのは、斉次方程式と非斉次方程式では当然斉次方程式の方が解きやすい。非斉次方程式の方の解は一つだけ求めておいて、斉次方程式の解を見つけられる限り見つけておけば、重ねあわせによって非斉次方程式の解をたくさん（見つけられる限り）見つけることができるようになる。

　簡単な例をやってみよう。${\mathrm d\over\mathrm dx} {y}= {x}+{y}$という線形非斉次微分方程式を解きたい。これは「変数分離できる形」にはなってない。そこで試行錯誤で解を探す。たとえば${y}=a{x}+b$が解になるだろうか、と考え代入してみると、 \begin{equation}\begin{array}{rl} \overbrace{a}^{\tiny {\mathrm d\over\mathrm dx} {y}}=& {x}+\overbrace{a{x}+b}^{{y}} \\ 0=&(1+a){x}+b-a \end{array} \end{equation} となるから、\文中式{$a=-1,b=-1$}にすれば解となる。

　ここはノートで計算してもらい、自由に話し合っていいからということでしばらく見ていたが、$0=(1+a){x}+b-a$まで行ってもこの後どうしよう？？と悩んでいる人が（中には$x={a-b\over 1+a}$とかする人も）いた。
　しかしここで「${y}=a{x}+b$が解になるだろうか？」と考えたのは仮定であって、ある意味「勝手に決めてみた」のだから、$a$や$b$の値も「勝手に決めればいい」ものなのである。だから、$1+a=0,b-a=0$としてしまえばよい。

　ゆえに、${y}=-{x}-1$という解が見つかったわけだが、ここで「バンザイ、解が見つかった」と終わってはいけない。なぜならこの解は「特別なある１つの解」であって、全ての解を求めていない。

関数${y}=-{x}-1$は

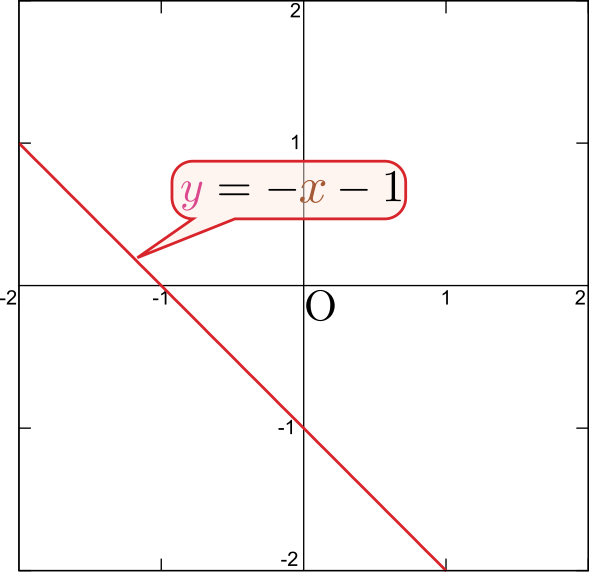
のようなグラフであり、この線の上という（全${x}$-${y}$平面から見たらほんとに狭い）範囲の上での「解」を求めたに過ぎない。この解は「特解」であり、我々が求めたいのは全${x}$-${y}$平面を埋め尽くす、「一般解」である。

　非斉次になっているのは${x}$という項のせいだから、これを消して${\mathrm d\over\mathrm dx} {y}= {y}$という斉次方程式を作る。この方程式の解は、何度も出てきているお馴染みの \begin{equation} {y}=C \mathrm e^{{x}} \end{equation} である。非斉次方程式の解は特解にこの斉次方程式の一般解を足せば作ることができる。

　すなわち、一般解は \begin{equation} {y}=-{x}-1 + C\mathrm e^{{x}} \end{equation} となる。$C$を$0.5$ずつ変えた線を示すグラフが次の図である。

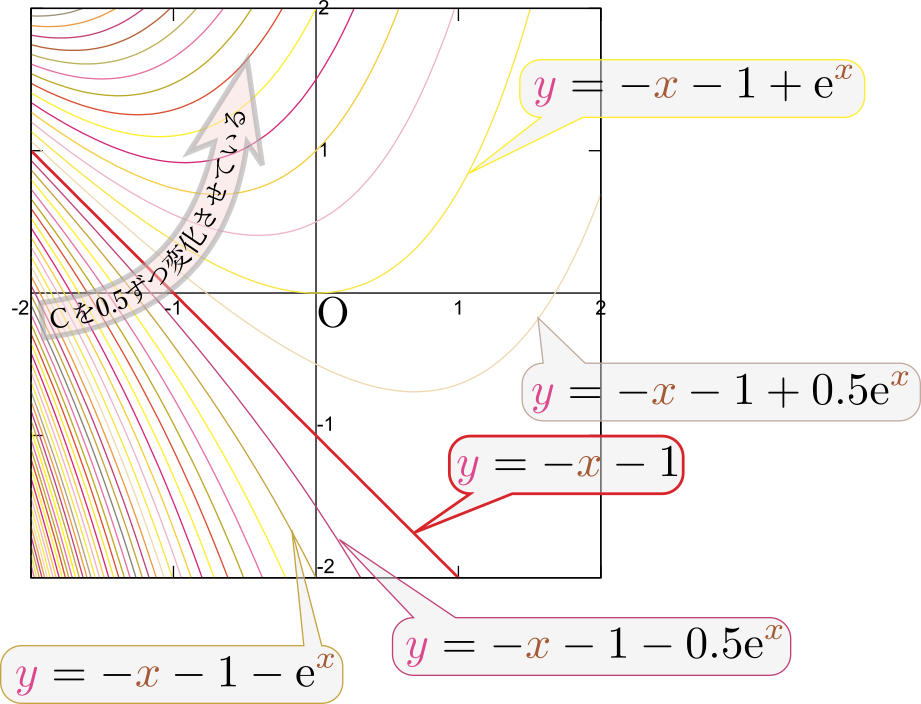
　描かれている線と線の隙間にも線があり、解の曲線は全平面を埋め尽くし埋め尽くしていることを確認するには、任意の点の座標$({x},{y})=(x_0,y_0)$を代入すると必ず一つ$C$が決まることを見る。この場合なら、$C=(y_0+x_0+1)\mathrm e^{-x_0}$である。微分方程式の形によっては解の曲線が通らない領域が存在することもあり得る（例えば、${\mathrm dy\over {\mathrm dx}}=\sqrt{1-{x}^2}$は$|{x}|>1$では解がない）。、どのような初期値$(x_0,y_0)$から出発しても、微分方程式に従うその後の変化がわかる。重ねあわせの原理のおかげで以上のような計算ができる。

　たとえば三角関数とかも重ね合わせの原理を満たすんですか？
　「三角関数」というだけでは重ね合わせできるかどうかはわからなくて、どんな微分方程式の解になっているかが大事です。重ねあわせの原理というのは、微分方程式で決まるもので、関数で決まるもんじゃないので。たとえば音の方程式（光でもいいけど）は三角関数が解になっていて、しかも重ねあわせの原理を満たしますね。音の方程式はこの授業の最後の方でやりますが、そのときは三角関数が出てきて、しかも重ねあわせできます。
ここでやったことは以下のように考えてもよい。まず特解${y}=-{x}-1$を見つけたから、「実際の解は特解に近い形をしているだろう」と推測し、「とりあえず特解に未知の関数${Y}$を足したものが解だろう」とあたりをつけて、${y}=-{x}-1+{Y}$と置いてみる。これを元の微分方程式に代入すれば、 \begin{equation} \begin{array}{rl} {\mathrm d\over\mathrm dx} \overbrace{\left(-{x}-1+{Y}\right)}^{{y}}=& {x}\overbrace{-{x}-1+{Y}}^{+{y}} \\ {-1} + {\mathrm d\over\mathrm dx} {Y}=& {-1} + {Y} \end{array} \end{equation} となるから、後は${\mathrm d\over\mathrm dx} {Y}={Y}$という微分方程式を解けばよい。
受講者の感想・コメント

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

予想が外れたら終わりだと思いました。グラフにしてみたら理解が深まった気がしました。
「終わり」じゃないよん。そのときは「次の予想」を試すんです。あきらめてはいけない。

変数分離以外で解くのって難しそうだなーと思いましたが、いざ授業を聞くと納得できました。ただ見つけるのがたいへんそうでした。
特解を見つけるのは試行錯誤です。

先生の話を聞いて、なぜリニアモーターカーはあんな形なのにカーというのかという疑問は電車に車と入っているという疑問と線型結合できることがわかりました。ありがとうございます。
ううむ。その話に「線型結合」っているんだろうか？？

線形斉次微分方程式の重ね合わせの原理についてわかった。また、非斉次方程式のばあい、斉次方程式の一般解と非斉次方程式の特解の足し算によって一般解が導かれることがわかった。
「わかった」で終わらず練習しておいてくださいね。

ちょっと感覚的な表現が多くてむずかしかったが、何回かやるうちにわかってくるものなのだろうか。
「感覚的」？そうかな、いろんな言葉が出てきたけど、定義はしっかりしていると思うけど。まぁ何事も自分の手でやっていかないとわかるようにはなりません。

重ね合わせの原理を理解した。
使っていきましょう。

式全体を見て、より楽をするような柔軟な考えがなかったので、頭のマッサージをしてやわらかさを手に入れたい。
計算は自由にいろいろやってみることです。

がんばります。
がんばりましょう。

重ね合わせの原理などすぐ忘れてしまいそうなのでしっかり復習していきたい。
これから先ずっと使いますよ。

音は本当に打ち消し合わないのでしょうか？
重なっている間は打ち消しあったとしても、互いを通り過ぎるとまた元の形に復活します。

重ねあわせの原理という便利な性質から斉次と非斉次の和の一般解を求めることができた。
自分でやってみておいてください。

最初は重ねあわせの原理が便利な理由がわからなくてふてくされてたけど、${\mathrm dy\over \mathrm dx}=y+x$を解いてから、ふてくされていた自分を殴りたくなるくらいに理解できました。ありがとうございました。
ふてくされてたのか(^_^;)。まぁ最後では理解できてよかった。

非斉次方程式や斉次方程式など、新しい言葉がでてきたのでしっかり覚えたい。
「覚えたい」という勉強をしてはだめ。人は覚えたことはすぐ忘れる。「理解する」ことが大事。

今日は全然眠くなかったので線形微分方程式の解き方が理解できました。
いつも眠くならないでいて欲しい。

重ねあわせの原理を初めて知って、こんな微分方程式の解き方があるんだなぁと思った。
いろいろあるんですよ。

これから重ねあわせの原理を用いて問題を解くことが増えていくと思うので、演習を通して理解を深めたい。
どんどん問題を解いてみてください。

難しい言葉を覚えた。
「覚えた」ではダメで、「理解した」まで行って欲しい。

「線形微分方程式」という言葉は何度も目にしてきたが、意味は全くわからなかった。今回の講義で少し意味を理解できたのでよかった。
難しいものではないでしょ。あとは解き方を理解しよう。

重ねあわせの原理は便利だなと思いました。でも見つからない場合は面倒そうだなと思いました。
便利です。見つからないときの方法は、また今度。

$y=\underbrace{A\mathrm e^x}_{非斉次の一般解}\underbrace{-x-1}_{~斉次の一般解}$を理解して、他の問題にも応用していきたいです。
ただしくは、$y=\underbrace{A\mathrm e^x}_{斉次の一般解}\underbrace{-x-1}_{~非斉次の特解}$ね。応用はいろいろあるので、やってみてください。

線形斉次微分方程式分かってよかったです！いろんなことが物理と関わっていくと思ったら楽しいです。
物理ではすごく御世話になります、今日の解き方。

重ねあわせの原理はすごい発見だと思いました。演習の中で使い方をつかみたいと思います。
いろいろやってみてください。

変数が二つあっても微分方程式が解けるということがわかった。難しい言葉はたくさん出てきましたが、中身は簡単だった。
そうです、中身は簡単です。

微分方程式の解はどうして線形結合したものも含まれるのかが今まで疑問に感じていたが、今日ですっきりした。強制振動の方程式もこれですんなり解けると思う。
理屈は単純でしょ。強制振動は時間があればこの授業でもやります。

重ねあわせの法則を用いて、いろいろな数式を微分したいと思った。
う〜〜〜ん。重ねあわせの原理は、微分に使うもんじゃないんだけど。

新しい習った線形微分方程式を使いこなせるようにしていきたい。
使いこなしましょう。この後何度も出てきます。

特解というのは、一つの解から方程式から導き出したものですか。今回の重ねあわせの原理は$y_1+y_2=A\mathrm e^x-x-1$ということで、$y_2$の一般解が$y_2=-x-1$ということですか。
いや「特解」ってのは「一つの解」ってこと。「$y_2=-x-1$」が特解（一般解じゃない）。

変数分離で微分方程式を解けるようになったけど、変数分離ができない方程式の解き方を学んだので、これからいろいろ線形性の微分方程式を解いてみたいと思います。
解いてみてください。ただ、どっちでも解けない微分方程式も世の中にはあります。

斉次・非斉次方程式が最初はよくわかりませんでしたが、最後は納得できました。
解き方の違いを理解しておきましょう。

特解を使って解を見つけるのは面白いと思いました。うまく特解を見つけられるよう勉強したいと思います。
練習しよう。

線形微分方程式は言葉だけでは難しそうだと思ったが、解けてすっきりした。とにかく一つでも特解を見つけることが重要だと分かった。音が伝わるのも重ねあわせの原理が使われていることを知った。
線形微分方程式は使い途が多いです。

重ねあわせの原理という今まで聞いたことのない新しい解き方におどろきました。慣れたいです。
今後何度も何度も何度も出てくると思います。

非斉次方程式の解を頑張って一つだけ求めないといけないと聞いたとき、難しそうだと思ったけど、$y=ax+b$と勝手に仮定することで、簡単に求めることができたので、驚いた。
まぁ、最初だから簡単な式を選んだんですけどね(^_^;)。

線形非斉次微分方程式は難しかったです。斉次と分けて考えるということをすると分かりやすかったです。
これからもどんどん使いますよ。

先入観を持っていた「重ねあわせの原理」がこんなに使い勝手のいいものだとは思わなかった。あと、髪色を青にしてみました。どうでしょうこの髪。
重ねあわせの原理はこれからもどんどん使いますよ。髪については、そういうのに興味ない私に聞かれてもなぁ。まぁ、「おおっ」とは思いました。

重ねあわせの原理、便利ですね。非斉次方程式の特解の求め方がやや難しかったです。
特解を出すのはとにかく試行錯誤です。

重ねあわせの原理はやり方を聞いていたらあたりまえのことだとおもうけど、線形結合と解くときになると、とても便利だと思った。
便利なので使えるときはどんどん使いましょう。

${\mathrm dy\over\mathrm dx}=x+y$を斉の解＋非の解＝一般解（非の解）で計算すると簡単に$y$の方程式を立てることができた。斉の解は「特解」で非の解は「一般解」であることがわかった。
最後のは逆。「斉次の一般解」と「非斉次の特解」を足します。

重ねあわせの原理が色々応用が聞いて興味深かった。またとにかく特解を求めることが方程式を解くうえで重要なのだとわかった。
重ねあわせの原理は今後も重要です。

新たな知識を得ることができた。
「知識」で終わらせず、見につけて「自分の技術」にしましょう。

線形の重ねあわせの原理をしっかり使えるようになりたい。
使えるようになりましょう、きっと役に立つ。

線形非斉次微分方程式の一般解を線形斉次微分方程式の一般解と線形非斉次微分方程式の特解で解けることがわかった。
練習してみてください。

微分方程式が簡単に見えてきました。
できるようになれば、なんだって簡単に思えるものです。ただ、微分方程式は「奥が深い」のでこの先いくらでも難しいのが出てきますよ。

重ねあわせの原理は便利だなと思いました。
便利だし、これからもよく使います。

重ね合わせの原理を解くを理解すると、斉次と非斉次の重ねあうの場合は、まず一部未知部分を隠して残った部分の特解を求めて、最後原方程式に解くという方法かと考えた。
まずは非斉次部分を消して（問題を簡単にして）解いて、後で補正していく、という感じです。

線形微分方程式