青字は受講者からの声、赤字は前野よりの返答です。
3種類の運動は、2次方程式の判別式で決定できることを知り、中学時代の勉強が役だったとうれしい。
判別式って、他のところでも結構出てきますよ。
復習して理解できるようがんばります。
はい、がんばって。わからないところは質問にきてください。
昔から不思議だったのですが、微積分の記号化による単純な計算で不可思議に微分積分の答えが出る! つまり、数学の記号は言語なのでしょうか?
数学の記号は立派に「言語」だと思います。面白いのは、記号を操作するということをやっていくとちゃんと答えが出てくるところですね。数式を使うと考えもしなかった答えが出てきてびっくりすることもよくあります。
$m{\mathrm d^2x\over\mathrm dt^2}=-K{\mathrm dx\over\mathrm dt}-kx$は$x=\mathrm e^{\lambda x}$として代入して計算する。虚数解の存在も意識して場合分けを考える必要があると思った。
今回の場合、虚数が入っているところから、重要な結果が出てますからね。
最後の方の授業スピードくらいでも大丈夫です。
そう? もっとも最後のあたりはスピードの問題より、結論までいかなかったのが消化不良だったかもしれない。
まだ理解ができてないので復習がんばります。
自分の手でどんどん計算してみてください。
最終的には何種類の文字だいたいの現象を記述されるのかは自然からしたらたまったもんじゃありませんね。
少ない変数でたくさんの現象がわかるのは人間にとっては嬉しいことですね。
複素数があるように見えてないのもあるとわかった。
複素数が出てきても、そこで計算をやめてはいかん、ということです。
やっぱり面倒な式を解くときは面倒な方法で解くのだとわかった。解くためにいろいろな工夫がなされているのはわかったので、もう一度家で復習してきます。
「面倒くささ保存の法則」がありますので、面倒な式は面倒な作業をして解いてください。
今まで学習してきたほどとほとんど全部使って解いていくのでとてもやりがいがありました。復習もちゃんとやっておきます。
じっくり計算してみてください。
複雑になってきたので頑張ります!
がんばりましょう。
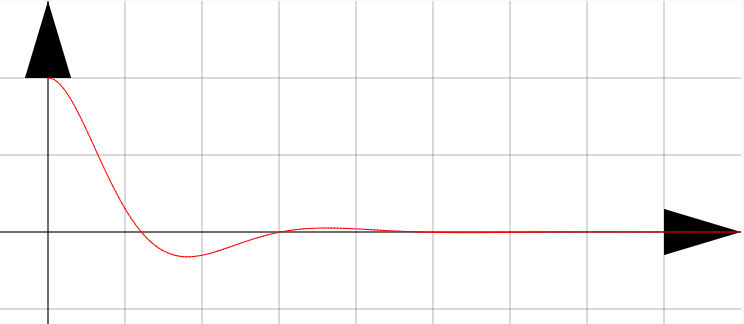
減衰振動や臨界振動のイメージをしっかり固められた。振動の運動方程式の解き方を復習できた。
イメージと計算をしっかり身につけてください。
計算過程がすごく難しく感じました。計算たくさん練習します。
一度自分の手でやってみてください。なれたら「すごく難しい」とまでは感じなくなります。
一階線形微分方程式は、何回も練習しないと慣れないと思った。
何回も練習しましょう、みんなそうやってきたのです。
振動する場合としない場合の間の状態も微分方程式を解けた見つけられるのは驚きました。
数式で計算することの威力です。
計算で文字がたくさんでてきて混乱することもあったけど、一つ一つ式を見ていくとやっていることが理解できた。
じっくり見れば、そんなに難しくないはずです。
$x=\mathrm e^{\lambda t}$の使い方と実数解、虚数解の解き方はもう一回理解できました。ちょっと慣れてきたと感じました。
繰り返し練習して、なれていきましょう。
今日は朝からゲロを見たのでテンション下がりまくった状態での講義でした。
(´・ω・`)知らんがな。
遅刻してしまった…。次回はしないように努力したい!
ちゃんと授業に出ようね。
今日の講義は、最初のバネの問題で場合分けをしっかりしようと思いました。つい解が出たらそこで終わってしまうので、気をつけたいです。最後の問題も復習したいです。
ちゃんと考えていけば、正しい答えが出ます。
空気抵抗のあるバネの振動についてアンドロイドの図によりわかった。
動きで理解しておきましょう。
線形結合があいまいなので見直す。
たいして難しい話ではありません。「定数倍して足したり引いたりしてできるもの」です。
今日は久々に数学が楽しかった。やっぱり現象が見える数学でなければと思う。
たいていの数学は現象を扱っているので、式の後にある現象を見るようにしましょう。
変換が多くて、理解できたかあやしい。これは何回か復習しておこうと思いました。
自分で何度かやってみてください。手を動かしていけば理解できます。
今日の微分方程式も楽しかったです。やはり、グラフで見えるととてもわかりやすいです。
数式とグラフを結びつけて理解していきましょう。
少し前まで金髪だったのですが、最近黒染をしました。
そうですか(←全然気づいてない)。
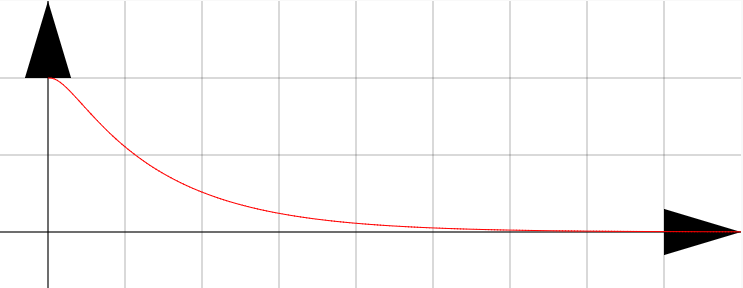
バネの振動の式は空気抵抗を考慮すると2次方程式の解のルートの中を正負0の場合に分けなければならないと分かった。定数係数でないときの一階微分方程式はなんとかしてイコール0の形に組み替えれば解けると分かった。
自分でやってみてください。
微分方程式(定数係数)を解くことができるようになっているが問題を見てその式をたてる、ということがまだ確実でない。運動法定s気とかならできるが、以前やった流行の方程式などは、解説を見てやっと納得しているので、問題になれて正しい方程式を見つけることになれたい。
そこはやはり、どんどん解いて慣れていくことです。
途中で$p(x)$や$P(x)$やらで頭がごちゃっとなりましたら、一個一個丁寧に計算したらとてもスッキリ解けました。
実はそんなにたいへんな計算ではないです。
公式の導出過程をしっかり理解できた。
式は、「どう作るか」の部分が大事です。
後半の方が理解できなかったのでしっかり復習したい。
次回、続きをやります。
忘れている公式も板書してくれて、導出過程が理解できた。分かるところだけ着実に学んでいるので、全く手につかないのよりもしっかり微分について学べている。
着実に、前へ進んでください。
空気抵抗のある振動の微分方程式の解き方がわかった。グラフなどで実際に見ていると$K$と$k$の値によって大きくグラフが変わったので理解が深まった。
係数を変えると関数(解)が変わるというところをじっくり理解してください。
最後のやつが難しかったので、しっかり復習したい。
まずは自力で計算をしてみること。
理解を深めたい。
自分の手で計算をやってみてください(それが一番)。
バネの振動のしかたは1パターンしか最初は想像できなかったので、タブレットでみてみてすごいと思いました。
実際の振動だと(こんなに抵抗大きいのはないので)なかなか実現しませんね。
今日の後半の微分方程式はレベルがかなり上がったように思えました。めげずに復習します。
「一般的」にするとそれだけ難度は上がります。
難しかった。定数変化法はもう一度確認してみようと思った。
今日はまだ定数変化法まで行ってませんよ。
今日のは面白い計算のやり方だと思いました。なれてスラスラ溶けたら楽しそう。
じゃ、慣れて楽しく計算してください。
今日は空気抵抗を受ける振動子と定数係数ではない一階線形微分方程式を解いた。バネの振動を三つ(シミュレーション)確認できました。
シミュレーションでイメージをつけてくださいね。
難しくて理解できたか不明なので何回も復習したいと思う。
復習してください、自力で一回やってみれば、わりと簡単に理解できると思います。
空気抵抗があるときの単振動の運動を考察することができた。
考察やりつつ、計算で解いていくのがよいです。
アンドロイドで運動の様子が見られてイメージが湧いてとても助かりました。
イメージをつけておいてください。
遅刻してしまった。今日できなかった分を友人との復習で取り返したい。
おお、友人と話すのはお互い勉強になってとってもいいですよ。
iが消えてスッキリした。教科書読んで特性方程式あたりから整理したい。
じっくり復習してみてください。
微分方程式が定数係数でなくなっても、やることは似たようなもんなんだなぁと思った。
結局、これまでやってきたことを基礎にして次へと向かうわけです。