自然科学のための数学2015年度第28講

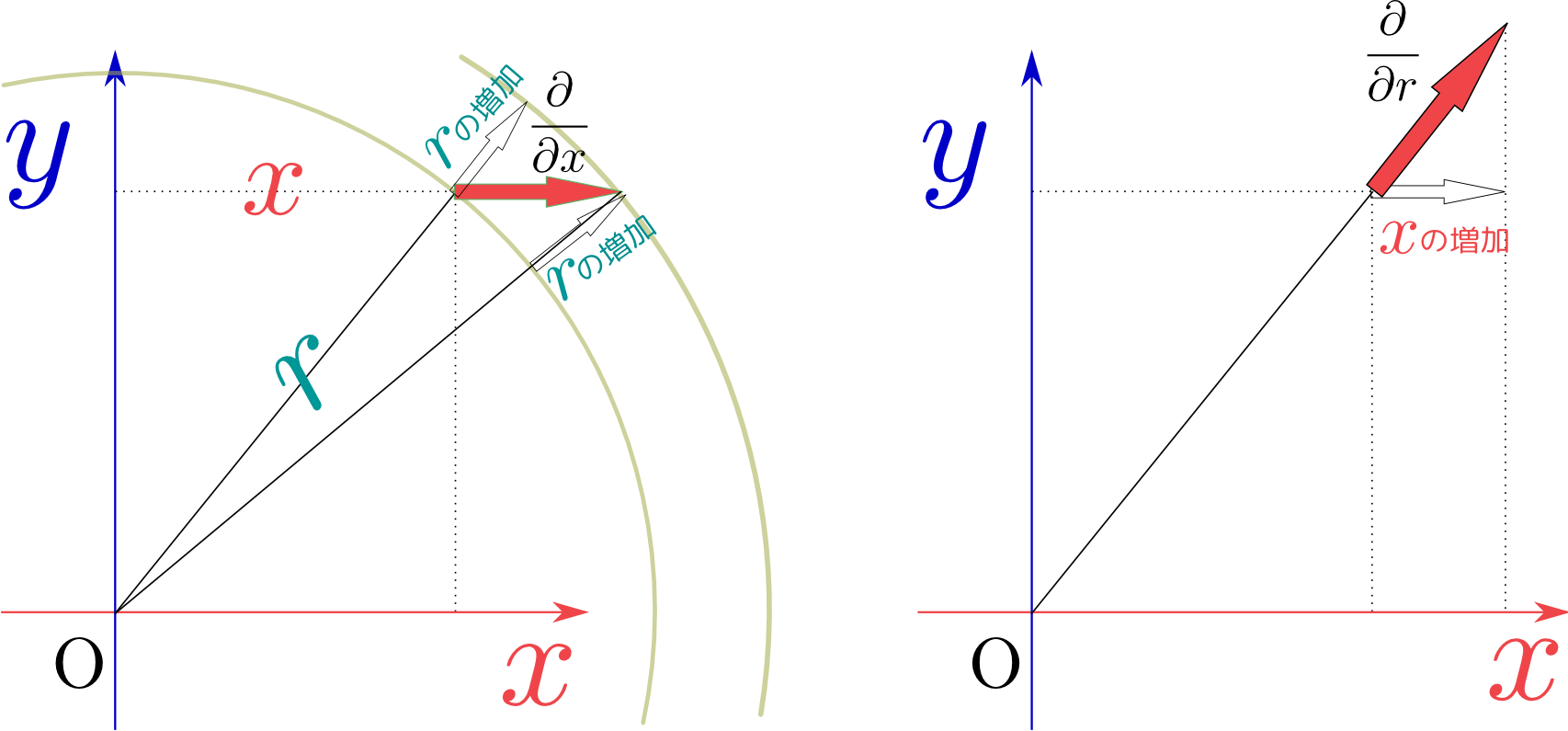
常微分と偏微分の違い（復習）

　「関数$f(x)$の微小変化」を表す量は、以下の式のように書ける。 $$ f(x+\mathrm dx)=f(x)+{\mathrm df\over\mathrm dx}(x)\mathrm dx $$ あるいはこの逆にあたる演算が $$ f(x_1)=f(x_0)+\int_{x_0}^{x_1} {\mathrm df\over\mathrm dx}(x)\mathrm dx $$ である。積分しているのは下の赤矢印の部分。

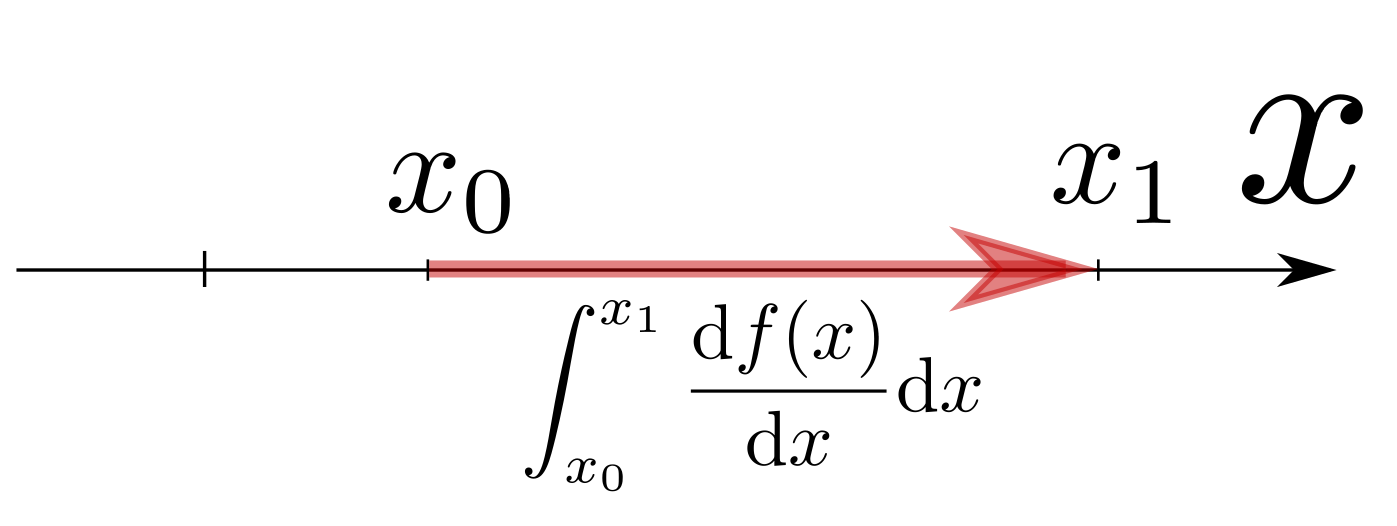
　これは$f(x_0)$を「元の値」、$\int_{x_0}^{x_1} {\mathrm df\over\mathrm dx}(x)\mathrm dx$を「変化量」と見れば、$f(x_1)$が「変化後の値」となる、という式であり、関数の変化の様子を微分と積分で表現していることになる。

　常微分（1変数）では変化は$x$が増えるか減るか、本質的には一つの方向しかない。

　「関数$f(x,y)$の微小変化」を表す量は、以下の式のように書ける。 $$ f(x+\mathrm dx,y+\mathrm dy)=f(x,y)+{\partial f(x,y)\over\partial x}\mathrm dx+{\partial f(x,y)\over\partial y}\mathrm dy $$ この${\partial f(x,y)\over\partial x}\mathrm dx+{\partial f(x,y)\over\partial y}\mathrm dy$の部分を「全微分」と呼ぶわけである。

　大事なことは偏微分には方向がある。ということである。

　さて、常微分における「微分の逆」の演算 $$ f(x_1)=f(x_0)+\int_{x_0}^{x_1} {\mathrm df\over\mathrm dx}(x)\mathrm dx $$ の偏微分バージョン（2変数バージョン）を考えてみよう。単純に、 $$ U(x_1,y_1)=U(x_0,y_0)+\underbrace{\int_{x_0}^{x_1} {\partial U(x,y_0)\over\partial x}\mathrm dx}_{積分１}+\underbrace{\int_{y_0}^{y_1} {\partial U(x_0,y)\over\partial y}\mathrm dy}_{積分２} $$ と考えるのは正しいだろうか。これはどのような「積分」を行っていることになるか、図を描いて考えてみよう。

　ここではしばらく図を描いて自由に討論しつつ考えてもらった。

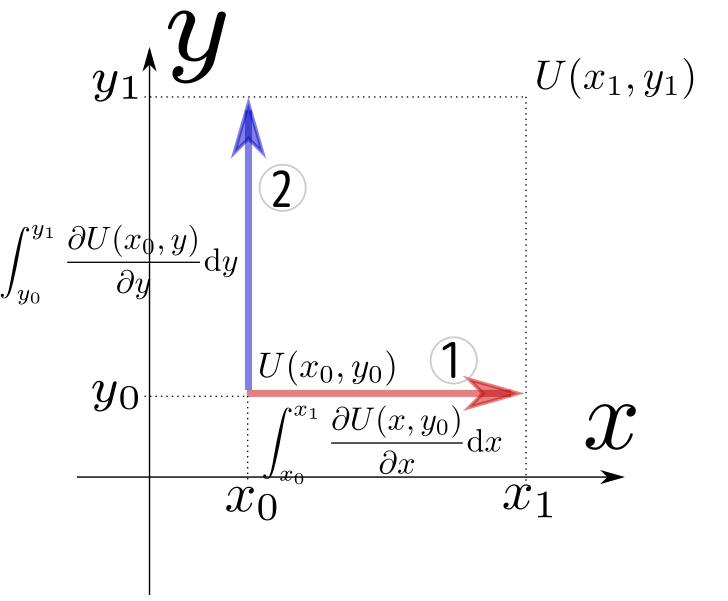
というような図を描いてみると「この積分は場所$(x_1,y_1)$に届いてない！」ことがわかる（だからこの計算で$U(x_1,y_1)$になるはずがない）。

$(x_0,y_0)$から出発してちゃんと$(x_1,y_1)$に届く積分としては、式で書けば $$ U(x_1,y_1)=U(x_0,y_0)+\underbrace{\int_{x_0}^{x_1} {\partial U(x,y_0)\over\partial x}\mathrm dx}_{積分１}+\underbrace{\int_{y_0}^{y_1} {\partial U(x_1,y)\over\partial y}\mathrm dy}_{積分３} $$ 図で書けば、

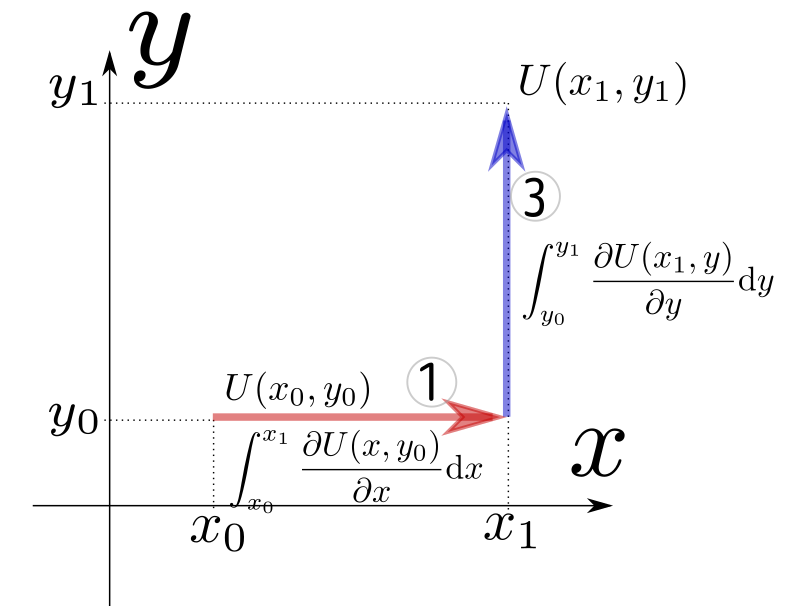
　または、式で書けば、 $$ U(x_1,y_1)=U(x_0,y_0)+\underbrace{\int_{y_0}^{y_1} {\partial U(x_0,y)\over\partial y}\mathrm dy}_{積分２}+\underbrace{\int_{x_0}^{x_1} {\partial U(x,y_1)\over\partial x}\mathrm dx}_{積分４} $$ 図で書けば、

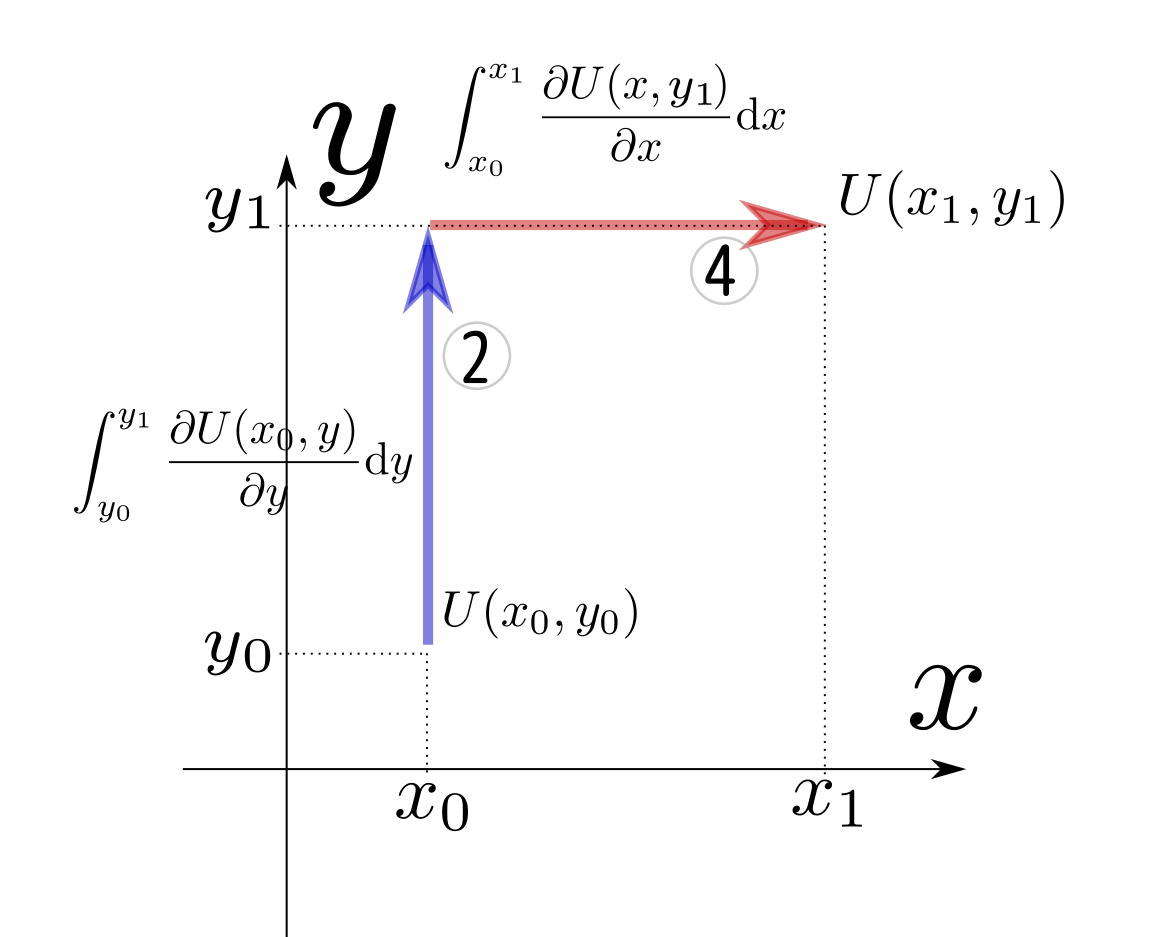
がある。

　つまりは、北東に進むために「まず東、次に北」と進んでもよいし、「まず北、次に東」と進んでもよい、ということ。実は斜めに進む方法（そういう積分のやりかた）もちゃんとある。

　このような積分は「線積分」と呼ばれる。

　この二つの積分が一致するのか？というのが気になるところである。それはつまり、

---

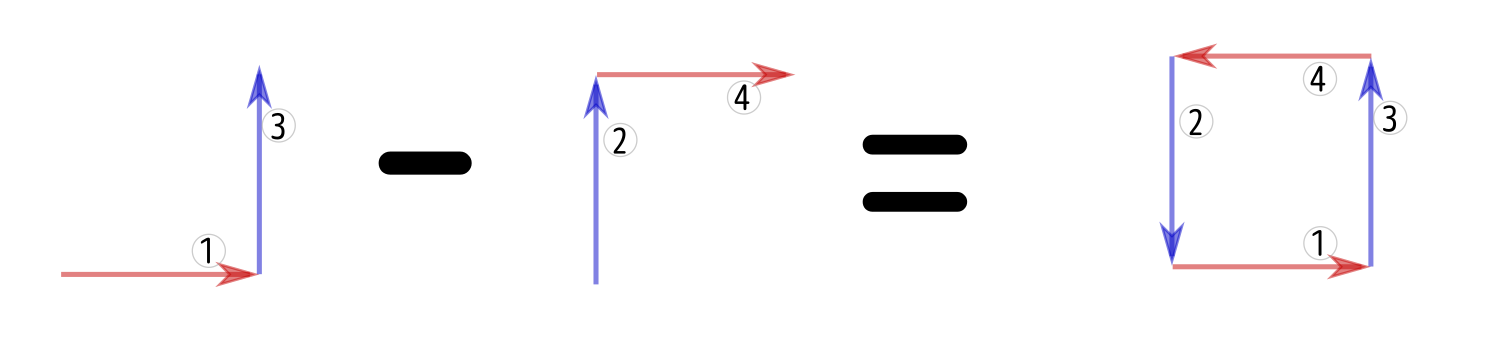
積分１＋積分３　　　は　　　積分２＋積分４　　　と一致するか？

---

という問題だが、これを少し変えると、

---

積分３ー積分２　　　は　　積分４ー積分１　　　　と一致するか？

---

という問題になる。そして、積分３ー積分２というのは、いわば積分３（$y$微分）の$x$微分である。同様に積分４ー積分１は積分４（$x$微分）の$y$微分であり、積分可能条件（あるいは、偏微分の交換）によればこの二つは等しい。

なお、これをさらに

---

積分１＋積分３ー積分４ー積分２　　　は0か？？

---

と読み替えると、これは「一周積分は0か？」を意味する。$U(x,y)$という関数が存在すれば、一周戻ってくれば$U(x,y)$も元の値に戻っている、ということを意味している。

　これはベクトル解析で言う「rot」である。

　これは位置エネルギーなどの「保存力の場」が満たすべき条件になっている

偏微分に関する注意その１

偏微分に関する注意その１

　 偏微分の計算を行うときに有用な公式と、誤りやすい注意点を述べておく。

---

よくある誤り

　極座標の計算で「${x}={r}\cos {\theta}$より${\partial {x}\over \partial r}=\cos{\theta}$と計算できる。ゆえに${\partial {r}\over \partial x}={1\over \cos{\theta}}$だろう」と考えてしまう。

---

　これに限らず、常微分であれば成立する${\mathrm dy\over \mathrm dx}={1\over {\mathrm dx\over \mathrm dy}}$との類推で、偏微分でも「分母」と「分子」を入れ替える$\left({\partial a\over \partial b}\to {\partial b\over \partial a}\right)$と逆数になると勘違いしてしまいがちである。

　実際に${x},{y}$を独立変数として$r$を\文中式{$r({x},{y})=\sqrt{{x}^2+{y}^2}$}としてこれから${\partial {r}\over \partial x}$を計算すると、 \begin{equation} {\partial {\left(\sqrt{{x}^2+{y}^2}\right)}\over \partial x} = {1\over 2\sqrt{{x}^2+{y}^2}}\times 2{x}={{x}\over \sqrt{{x}^2+{y}^2}}=\cos\theta \end{equation} となる。一方で、${r},{\theta}$を独立変数とすれば$x({r},{\theta})={r}\cos{\theta}$なので、 \begin{equation} {\partial {x}\over \partial r}= {\partial {\left({r}\cos{\theta}\right)}\over \partial r}=\cos{\theta} \end{equation} となる。つまりこの場合${\partial {r}\over \partial x}={\partial {x}\over \partial r}$なのだ。${\partial {x}\over \partial r}={1\over {\partial {r}\over \partial x}}$と誤解してしまうのは、省略記法を使っているからである。省略せずに書くと、${\partial {x}\over \partial r}$は$\left({\partial {x}({r},{\theta})\over \partial r}\right)_{{\theta}}$、${\partial {r}\over \partial x}$は$\left({\partial {r}({x},{y})\over \partial x}\right)_{{y}}$である。${}_{{\theta}}$と${}_{{y}}$に注意。「どの変数を固定しているか」は大事なのである。

　逆に「どの変数を固定しているのか」が同じであれば、常微分のときと同様に \begin{equation} \left( {\partial {r}\over \partial x}\right)_{{y}} = {1\over \left( {\partial {x}\over \partial r}\right)_{{y}}}\label{koteionaji} \end{equation} である（両辺ともに${y}$を一定とすることにした）。実例を一つ確認しよう。左辺は \begin{equation} \left({\partial {r({x},{y})}\over \partial x}\right)_{{y}}= \left( {\partial {\sqrt{{x}^2+{y}^2}}\over \partial x}\right)_{{y}} ={{x}\over \sqrt{{x}^2+{y}^2}}={{x}\over {r}} \end{equation} 右辺の分母は、${r}$と${y}$を変数と考えての微分だから、${x}=\pm\sqrt{{r}^2-{y}^2}$として、 \begin{equation}\left( {\partial {x({r},{y})}\over \partial r}\right)_{{y}}= \pm\left({\partial {\sqrt{{r}^2-{y}^2}}\over \partial r}\right)_{{y}} =\pm{{r}\over\sqrt{{r}^2-{y}^2} }={{r}\over {x}} \end{equation} となり、この二つは逆数である。

　この二つの微分が同じになることを図解で示すと以下のようになる。

　左の図では${\Delta r\over \Delta x}=\cos\theta$で、右の図では${\Delta x\over \Delta r}=\cos\theta$になっていることを確認しよう。

常微分と偏微分の違い 受講者の感想・コメント

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

積分可能条件