自然科学のための数学2015年度第30講
偏微分方程式
ここまで考えた微分方程式は常微分$\left({\mathrm d\over\mathrm dx},{\mathrm d\over\mathrm dt},\cdots\right)$を用いた微分方程式だったが、偏微分$\left({\partial\over \partial x},{\partial \over\partial y},{\partial\over \partial t},\cdots\right)$を用いた微分方程式もある。
常微分方程式の場合、積分していくことで解が求められた。この時積分定数という形で解に未定のパラメータが入った。たとえば常微分方程式${\mathrm d\over\mathrm dx} f({x})={x}$の解は$f({x})={{x}^2\over 2}+C$である。これに似た偏微分方程式 \begin{equation} {\partial\over \partial x}f({x},{y})={x} \end{equation} の解は$f({x},{y})={{x}^2\over 2}+C({y})$である。
常微分方程式なら独立変数(たとえば${x}$)の積分により解が出たから、${x}$によらない積分定数として解に現れた。$({x},{y})$の二つの独立変数を持つ偏微分方程式では${x}$の積分によって現れた積分定数は${y}$の関数であってよい(逆に${y}$の積分による積分定数は${x}$の関数であってよい)。
「微分して0$\Rightarrow$定数」ではないことが偏微分方程式の注意点である。
もう少しだけ複雑な例、 \begin{equation} \left({\partial\over \partial x}+a{\partial\over \partial y}\right)f({x},{y})=0 \end{equation} を考えよう。これの解の一つが$a{x}-{y}$であることはすぐに確認できるが、実は$F$を任意の1変数関数として、その引数に$a{x}-{y}$が代入された$F(a{x}-{y})$も解になる。というのは$F(a{x}-{y})$を、「${y}$を一定にして${x}$で偏微分」したものと「${x}$を一定にして${y}$で偏微分したもの」は$-a$倍違うから、 \begin{equation} \left({\partial\over \partial x}+a{\partial\over \partial y}\right)F(a{x}-{y})=0 \end{equation} が成立するからである。たとえば$\tan(a{x}-{y})$でも$\log(a{x}-{y})$でも、あるいは${(a{x}-{y})^5\over \sqrt{\sin(a{x}-{y})}}$のような複雑な関数でも、この偏微分方程式の解となる\footnote{分母が0になったりルート内が負になったりする領域が省かれるのはもちろんである。}。このような変数の組み合わせを見つけるというのも偏微分方程式の解き方である。
偏微分方程式の解き方
ここでは、求めるべき関数を$f({x},{y})$のように二つの独立な変数${x},{y}$によって決まる2変数関数として説明する。変数が${t}$になったり${r}$になったりしても考え方は変わらないし、3変数、4変数と変数の数が増えても、基本的には同様の手順で解いていく。
変数分離による解法
\begin{equation} \left({\partial\over \partial x},{\partial\over \partial y}を含む微分演算子\right)f({x},{y})=g({x},{y}) \end{equation} のような微分方程式が与えられた時、これの解をいきなり探すのは難しい。そこで、この方程式の解が$f({x},{y})=X({x})Y({y})$のように${x}$を変数とする部分と${y}$を変数とする部分の積になるだろう、と仮定してみる。その後計算した結果、 \begin{equation} \left({\partial\over \partial x}と{x},X({x})の式\right) = \left({\partial\over \partial y}と{y},Y({y})の式\right) \end{equation} のように左辺と右辺に${x}$と${y}$が分離できたとする(これを「変数分離」と呼ぶ)。この式が成立するためには左辺も右辺も定数にならなくてはいけない\footnote{${x}$と${y}$は独立変数で、勝手に変化できるのだから、左辺が${x}$によって変化し、右辺が${y}$によって変化したら、この式は運がいい時にしか成立しない式になる。}ので、その定数を$\alpha$と置いて、 \begin{equation} \left({\partial\over \partial x}と{x},X({x})の式\right)=\alpha,~~ \left({\partial\over \partial y}と{y},Y({y})の式\right)=\alpha \end{equation} という常微分方程式二つを解けばよい、というのが「偏微分方程式の変数分離」である。なお、変数分離で答が求まるというのはあくまで「仮定」であるから、これで正しい解が出ているかどうかについては注意しなくてはいけない。
$\alpha$は任意の定数だから、その定数に応じてたくさんの解が出るが、境界条件などにより実際の解がどのようになるかが決められる(このあたりは常微分方程式でもあったこと)。
「微分演算子の因数分解」による解法
常微分方程式の時に、「微分演算子の因数分解」を行って解く方法があったことを思い出そう。同様にもし我々がたとえば偏微分方程式の微分演算子を \begin{equation} \left( \left({\partial\over \partial x}\right)^2 +(a+b){\partial^2\over \partial x\partial y} +ab\left({\partial\over \partial y}\right)^2 \right)f({x},{y}) =\left({\partial\over \partial x}+a{\partial\over \partial y}\right)\left({\partial\over \partial x}+b{\partial\over \partial y}\right)f({x},{y})=0 \end{equation} のように`因数分解'して \begin{equation} \left({\partial\over \partial x}+a{\partial\over \partial y}\right) f({x},{y})=0 ~~または~~ \left({\partial\over \partial x}+b{\partial\over \partial y}\right)f({x},{y})=0\label{delfactoring} \end{equation} のように式を分離することができれば、問題を簡単化(二階微分方程式が一階微分方程式になった!)できる。
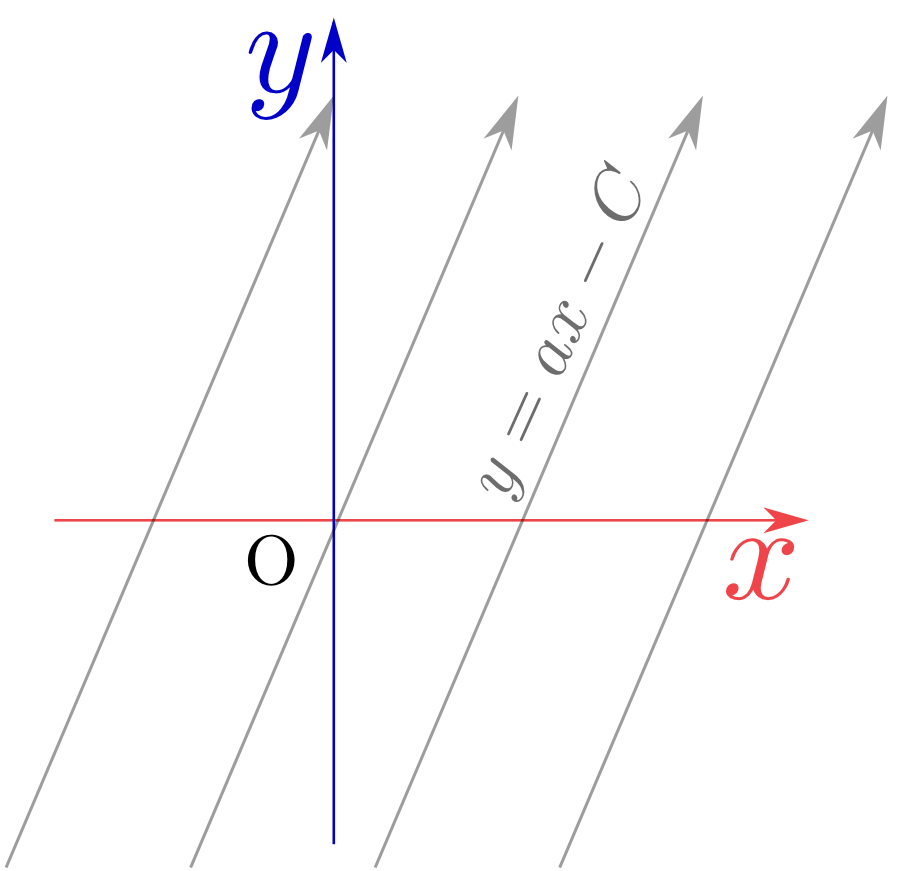
上の場合、第1の式の解は(任意の関数を$F$として)$F(a{x}-{y})$であり、同様にもう一つの解は(やはり任意の関数を$G$として)$G(b{x}-{y})$である。一般解は、$F(a{x}-{y})+G(b{x}-{y})$となる。
$F(a{x}-{y})$という関数は、$a{x}-{y}=C$($C$は定数)を満たす場所(つまり直線${y}=a{x}-C$上)では一定である。上で求めた解は、「直線${y}=a{x}-C$上で一定になる関数」と「直線${y}=b{x}-C'$上で一定になる関数」の和だということになる。
上の場合「直線」の上で解となる関数が一定となったが、 \begin{equation} \left( P({x},{y}){\partial\over \partial x} + Q({x},{y}){\partial\over \partial y} \right)f({x},{y})=0 \end{equation} のような偏微分方程式の場合、解である関数$G({x},{y})$を一つ見つけることができたなら、任意の関数$F(t)$の$t$に$G({x},{y})$を代入した$F(G({x},{y}))$もやはり解となる。この場合は、$G({x},{y})=C$(定数)であるような線(直線とは限らない)の上で$F$は一定となる。
微分方程式 \begin{equation} \left({\partial\over \partial x}+2{x}{\partial\over \partial y}\right)F({x},{y})=0\label{tokuseihoubutsu} \end{equation} は特性曲線が文字通り曲線になる例である。この微分方程式は一つの解として${y}-{x}^2$を持つ(代入して確認せよ)。よって、$f$は任意の微分可能な関数とすれば、 \begin{equation} F({x},{y})=f({y}-{x}^2) \end{equation} が解となる。${y}-{x}^2=(定数)$を満たす線(${x}=0$を軸とする放物線になる)の上で一定であるような関数なら全て解になる。
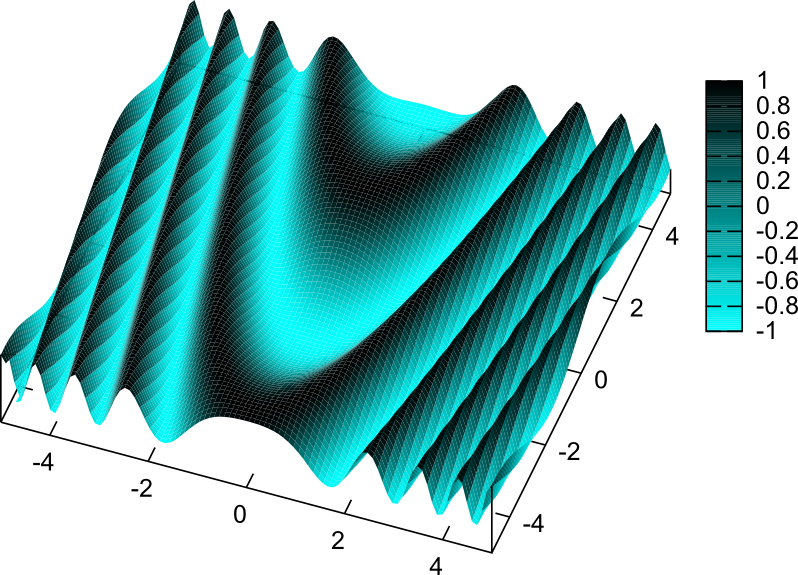
上の図は、$\sin({y}-{x}^2)$の3Dグラフである(放物線の上で一定になるような関数になっている)。
このような線(上の例では放物線)を「特性曲線(characteristic curve)」と呼ぶ。特性曲線を求めるということも、偏微分方程式の解法と言える。
「どんな関数でもよい」と言われると「解が求まってない」と心配になるかもしれないが、それは境界条件を指定していないからである。偏微分方程式も常微分方程式と同様に、方程式だけからは決まらないパラメータがあり、それを指定する必要がある。このあたりは以下でやる実例のところで説明しよう。
もう一つの例として、 \begin{equation} \left( {x}{\partial\over \partial y} -{y}{\partial\over \partial x} \right)f({x},{y})=0\label{tokuseien} \end{equation} を考えてみよう。今度は$({y},-{x})$という方向への微分が0ということである。この微分方程式の図形的意味から$\theta$方向に移動しても変化しない(特性曲線が円)という意味であることがわかるから、解は$f({x},{y})=F(r({x},{y}))$である($r({x},{y})$はもちろん極座標の$r$で$r({x},{y})=\sqrt{{x}^2+{y}^2}$という関係)。この解の偏微分係数を求めてみると \begin{equation} {\partial\over \partial x}F(r({x},{y}))=\underbrace{{\partial {r}\over \partial x}}_{{{x}\over r({x},{y})}}{\mathrm d \over \mathrm dr}F(r),~~~ {\partial\over \partial y}F(r({x},{y}))=\underbrace{{\partial {r}\over \partial y}}_{{{y}\over r({x},{y})}}{\mathrm d \over \mathrm dr}F(r) \end{equation} となり、${x}{\partial \over \partial y}F-{y}{\partial \over \partial x}F$という計算をすると0になることがわかる。
実はこの計算は(図形的意味が「${\theta}$方向に移動しても変化しない」だったことからもわかるように)、 \begin{equation} \left( {\partial\over \partial\theta}f(x({r},{\theta}),y({r},{\theta})) \right)_{{r}} = \underbrace{ \left({\partial {y({r},{\theta})}\over \partial \theta}\right)_{{r}}}_{{x}} \left({\partial {f}({x},{y})\over \partial y}\right)_{{x}} + \underbrace{ \left({\partial {x({r},{\theta})}\over \partial \theta}\right)_{{r}}}_{-{y}} \left({\partial {f({x},{y})}\over \partial x}\right)_{{y}} \end{equation} と表すこともできる。以上のことを一般化して、以下のことが言える。 \begin{equation} \left( P({x},{y}){\partial\over \partial x} + Q({x},{y}){\partial\over \partial y} \right)f({x},{y})=0\label{PdelQdel} \end{equation} のような形の微分方程式があったとき、 \begin{equation} \lambda({x},{y}) P({x},{y})={\partial {x({x},{y})}\over \partial X},~~~ \lambda({x},{y}) Q({x},{y})={\partial {y({x},{y})}\over \partial X}\label{PQlambdadel} \end{equation} となるような座標変換$({x},{y})\to({X},{Y})$を見つけることができたなら、この方程式に$\lambda({x},{y})$を掛けてから、見つけた式を使うことで、 \begin{equation} {\partial \over \partial X}f(x({X},{Y}),y({X},{Y}))= \left( {\partial {x({x},{y})}\over \partial X}{\partial \over \partial x} +{\partial {y({x},{y})}\over \partial X}{\partial \over \partial y} \right)f({x},{y}) =0 \end{equation} を得る。$f(x({X},{Y}),y({X},{Y}))$が${X}$を含まぬ${Y}$だけの関数が微分方程式の解となる。
「偏微分には方向がある」とここまで(少々くどく)述べたが、今日述べた微分方程式の解き方は「偏微分が0になる方向を探す」という方針の解き方である。
以下で具体的な偏微分方程式の例を述べよう。