対数関数の定義:指数関数の逆関数
10は2の何乗か? という疑問を考えた。より一般的に${x}$は${a}$の何乗か? という問題を考えることにしよう。つまり、${x}=a^{y}$という式が成り立つときに、${y}\to{x}$という対応関係を知りたい。つまり今考えたい関数は指数関数${y}=a^{x}$の逆関数であり、これを「対数関数」と呼ぶ。対数関数を表現するには、$\log$という記号を使う。一般的定義は
対数関数
1ではない正の定数$a$を底とする指数関数${y}=a^{{x}}$(${x}$が独立変数で${y}$が従属変数)に対し、${y}$を先に決めてそれに対応する${x}$を対応させる関数を対数関数といい、
\begin{equation}
{x}=\log_a {y}\label{defoflog}
\end{equation}
と書く(この式では、${y}$が独立変数で${x}$が従属変数)。
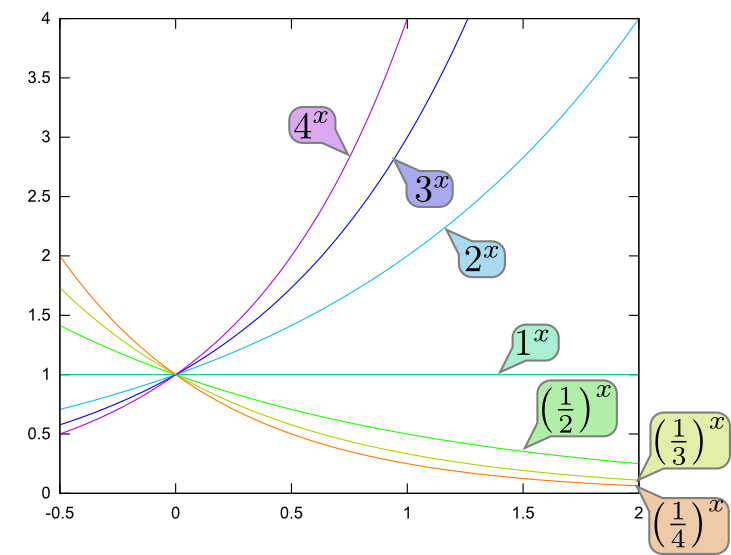
$\log_a$の$a$のことを指数関数の時と同様、「底(てい)」と呼ぶ。底が$2,{\mathrm e},10$およびその逆数${1\over 2},{1\over {\mathrm e}},{1\over 10}$の場合の指数関数(実線)と対数関数(破線)のグラフを下に示した(互いに逆関数になっていることを確認せよ)。
左右を見比べると、指数関数の性質$a^{-{x}} = \left({1\over a}\right)^{{x}}$ということが(${x}\to-{{x}}$という変化がグラフ上では左右反転となって)見て取れる。対数関数はこれの逆関数(${x}$と${y}$の立場が入れ替わる)だから、
\begin{equation}
\log_a {x} = -\log_{1\over a}{x}
\end{equation}
という関係がわかる(グラフでは上下反転として読み取れる)。
下に、例によって動くグラフがあるので動かしていろんな場合のlogのグラフを見ておこう。
上の青い線が 対数y =loga x 、薄い赤の線 が指数関数y =ax
この二つが互いに逆関数であることを確認しよう。
下↓のボタンでaの値を変えられるので、いろいろと変えてみよう(ただし、a=1.0は意味が無い)。
青い線:y =log2.0 x
薄い赤い線: y =2.0 x
指数関数と対数関数は逆関数である。しかし、$\log_a\left(a^{x}\right)=x$はどんな実数${x}$に対しても成り立つが、$a^{\log_a {x}}={x}$は、${x}\geq0$でないと今の段階では定義できていない(負の数の$\log$をちゃんと定義した後でなら考えられる)。
対数関数の公式
指数関数が持っていた「$\mathrm e^{{x}}$の肩の${x}$の足算は掛算になる」という性質は、対数においては逆になり、以下の式が成り立つ。
$\log$の引数の${掛算\atop 割算}$は$\log$の${足算\atop 引算}$になる
\begin{equation}
\log_a\left(x_1x_2\right)=\log_a{x_1} + \log_a {x_2}
\end{equation}
\begin{equation}
\log_a\left({x_1\over x_2}\right)=\log_a{x_1} -\log_a x_2
\end{equation}
上の式が確かに成り立つことは、$a^{\log_a(x_1x_2)}=x_1x_2$という式に$x_1=a^{\log_a x_1}$と$x_2=a^{\log_a x_2}$を代入してみれば、
\begin{equation}
a^{\log_a(x_1x_2)}=a^{\log_a x_1}\times a^{\log_a x_2}
\end{equation}
となるからわかる。
また、$(a^{x_1})^{x_2}=a^{x_1x_2}$となることから逆に、
冪の対数は底の対数の指数倍
\begin{equation}
\log_a x^b = b\log_a x
\end{equation}
もわかる。
なかなか対数関数($\log$)の「気持ち」がわからない、という人のために$10^{x}$を例にして説明しよう。
$10^2=100$は0が2桁、$10^3=1000$は0が3桁、$10^4=10000$は0が4桁、と増えていくことを考えると、${y}=10^{{x}}$という関数は
$n$を入れると「1の後ろに0が$n$個並んだ数」が出てくる関数
であるとも言える。ここで逆関数である${x}=\log_{10}{y}$は
「1の後ろに0が$n$個並んだ数」を入れると$n$が出てくる関数
という関数になる。すなわち、$10\to1,100\to2,1000\to3,\cdots,100000000\to8,\cdots$のような対応関係(言わば、「桁数$-1$を求める関数」である)が、${x}=\log_{10}{y}$という関数が表現する対応関係の「一部」である(実際には${x}=\log_{10}{y}$の${y}$には正の実数なら何を入れてもよいから、もっと広い範囲で使える)。
「車の修理代が6桁もかかったわ〜」「え〜っ」のように、数字の大きさを「○桁」で表現することはないだろうか。あれが$\log$の考え方なのである。
対数関数は「掛算の簡略化」にも使える。たとえば$1000\times 1000=1000000$だが、これを「0が3桁ある数字と0が3桁ある数字を掛けたから、0が6桁ある数字になる」という計算をすることができる。こう考えると、積の対数関数を対数関数の和に直す式を、
\begin{equation}
\log_{10} \underbrace{1000000}_{0が6つ}=\log_{10}\underbrace{1000}_{0が3つ}+\log_{10}\underbrace{1000}_{0が3つ}
\end{equation}
のように理解できる。
この「掛算の簡略化」は小学生で掛算を勉強した時にみんなやった筈。これが「対数」の考え方の基本とつながっている。
このやり方は$10^n$($n$が整数)の場合しかできないが、そうでない場合に拡張することはできる。なお、$\log_{10}{x}$のように底を10にした対数関数を「常用対数(common logarithm)」と呼ぶ。$\mathrm e$を底にした対数関数$\log_{\mathrm e}{x}$は「自然対数(natural logatithm)」である。以後、$\log{x}$のように底を省略した場合は自然対数である。
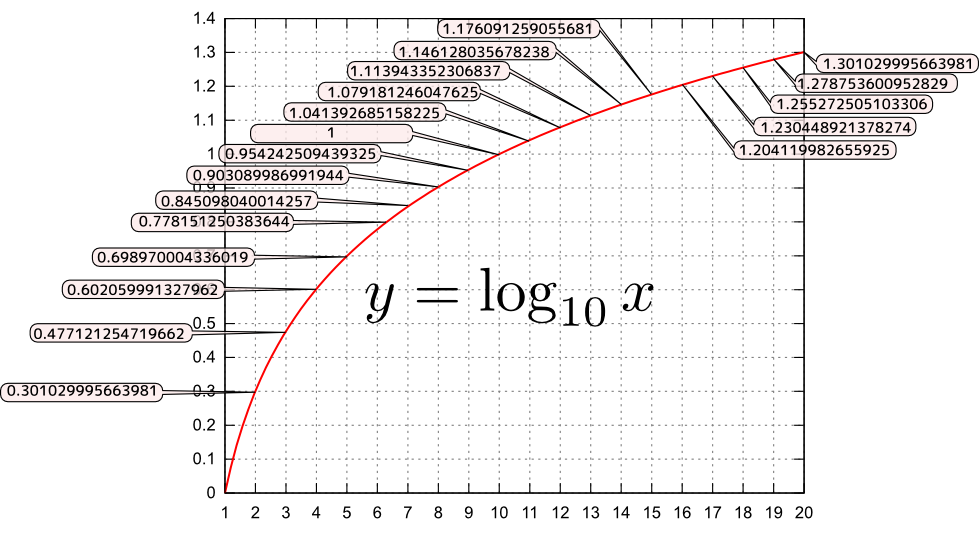
下に、${y}=\log_{10}{x}$の、${x}=1$から${x}=20$までのグラフを示した。
図を見て、たとえば$\log_{10}2+\log_{10}3=\log_{10}6,\log_{10}2+\log_{10}5=1$あるいは$\log_{10}9=2\log_{10}3$などのように、「掛算が足算に翻訳されること」を確認しよう。
$\log_{10}$の値を前もって調べておくことができると、例えば$5343342\times234234234$という計算を
\begin{equation}
\log_{10} \left(5343342\times234234234\right)
=\underbrace{\log_{10} 5343342}_{6.7278\cdots} + \underbrace{\log_{10} 234234234}_{8.3696\cdots}
\fallingdotseq15.0974\label{daitailog}
\end{equation}
のように、対数を介することで足算を使って実行できる。逆に$10^{15.0974}$を計算すれば、1251411091802385を得る。この値は、真面目に計算した結果の1251593620370028と比べて、4桁めまで正しい
上の計算を大雑把に$5000000\times200000000$として答えを見積もると以下のようになる。
対数関数は「桁数で比較する」という感覚で使われるわけだが、これは概算しているというわけではなく、大きさの変化があまりに大きい物を比較する時に便利な方法であるとも言える。たとえば地球の質量は$5.97\times 10^{24}$ kg、太陽の質量は$1.99\times 10^{30}$ kgである。これを普通の数字で書けば
\begin{equation}
\begin{array}{rr}
地球の質量:&約5970000000000000000000000 {\rm ~kg}
\\
太陽の質量:&約1990000000000000000000000000000 {\rm ~kg}
\end{array}
\end{equation}
なのだが、こう書かれるよりむしろ$10^?$の形で書いて肩に乗った24や30を見た方が「ああ約$10^6$倍程度違うんだな」ということが実感しやすい(というより、そういう感覚を持てるようにならないと、大きさの違いが甚だしい量を比較できるようになれない)。
対数関数の底の変換
指数関数同様、対数関数も底を変換したいことがよくある。
指数関数の底は$a=b^c$の時、$a^{x}=b^{c{x}}$ のように変換したから、${y}=a^{x}=b^{c{x}}$とおいて、$\log_a{y}$と$\log_b{y}$を計算すると、
\begin{equation}
\log_a {y}= {x},
~~~\log_b {y}= c{x}
\end{equation}
という式が出て、$c \log_a {y}= \log_b {y}$とわかる。ここで${y}=a$とすると、$c=\log_b a$である(この式は$a=b^c$からもわかるし、$c \log_a {y}= \log_b {y}$に${y}=a$を代入しても出てくる)から、
\begin{equation}
\log_b a \log_a {y}= \log_b {y}
\end{equation}
となり、
対数関数の底の変換
\begin{equation}
\log_a {x}= {\log_b {x}\over \log_b a}= {\log {x}\over \log a}
\end{equation}
という公式を得る(最後の形では分母分子とも自然対数にしている)。
なお、以上で使った計算で$a=b^c$の時$c=\log_b a$だったので、$b={\mathrm e}$を代入してできる式$a={\mathrm e}^{\log a}$をさらに${x}$乗して、
\begin{equation}
a^{{x}}={\mathrm e}^{(\log a){x} }
\end{equation}
という式を作ることができる。つまり全ての指数関数は($2^{x}$だろうが、$1991^{{x}}$だろうが)適切な係数をつけた${\mathrm e}$を底とする指数関数(${\mathrm e}^{k{x}}$)の形で表現できることになる。実は${\mathrm e}^{なんとか}$の形の関数が一番扱いやすいことが後でわかるので、どんな指数関数でもこの形で考えられるというのは朗報なのである。
残りの時間で微分の導入をやったが、今日はとりあえず、ここにあるアニメーション「微分ってなあに?」 と同じ内容のandroidアプリで、微分が「関数のグラフの傾きを計算する」ものであることと、そのイメージを感じてもらうところまでを行った。
特に、その4 のところで見せた「ややこしそうに見える関数も十分拡大すれば(つまり、Δxが小さい場合を考えれば)直線とみなせる」というところが大事である。