前期の復習
今日はガイダンスと、前期の復習(たぶん、夏休みで頭が錆びついちゃってる人がたくさんいるだろうと思ったので)をやりました。
微分とは何か
まず最初に聞いてみたのは
ってこと。
いろんな答えが出たのだけど、要は二つの変数$\xcol{x}$(独立変数)と$y$(従属変数)があったとき、 $$ {\ycol{y}の変化\over \xcol{x}の変化} $$ を考えて、かつ変化量が0になる極限(つまり、狭い範囲で考える)を取ったものである。
グラフで書くと傾きという量になる。
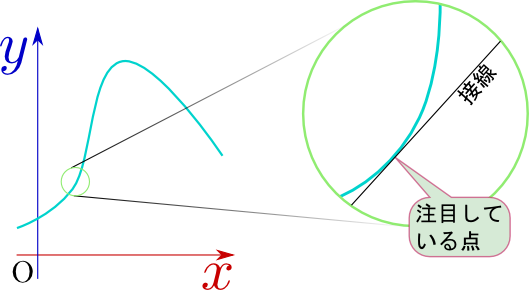
注目している点に引かれた接線の傾き、と考えてもよい。
ここで、プログラムを使って微分のイメージをつかんだ。
プログラムで実感して欲しいことは、「関数は狭い範囲だけを考えれば直線と近似して考えても差し支えない」ということ。
式で表現すると、関数$y=f(\xcol{x})$があったとして、この独立変数$\xcol{x}$が$\xcol{x}+\xcol{\mathrm dx}$と変化したとき、 $$ f(\xcol{x}+\xcol{\mathrm dx})=f(\xcol{x})+\underbrace{f'(\xcol{x})}_{微分}\xcol{\mathrm d x}\underbrace{+\cdots}_{無視する部分} $$ のように、関数の変化量が$\xcol{x}$の変化量である$\xcol{\mathrm dx}$に比例する。その比例係数が微分または導関数と呼ばれる、$f(\xcol{x})$なのである。
では簡単な実践編をやってみよう。$f(\xcol{x})=\xcol{x}^2$の場合、これが微小変化して $$ f(\xcol{x}+\xcol{\mathrm dx})=(\xcol{x}+\xcol{\mathrm dx})^2 $$ となったとする。右辺を展開すると、 $$ f(\xcol{x}+\xcol{\mathrm dx})=\underbrace{\xcol{x}^2}_{f(\xcol{x})}+\underbrace{2\xcol{x}}_{f'(\xcol{x})}\xcol{\mathrm dx}+\underbrace{(\xcol{\mathrm dx})^2}_{高次の微小量} $$ となる。「高次の微小量」の部分は無視する。これで$f(\xcol{x})=\xcol{x}^2$の微分(導関数)が$f'(\xcol{x})=2\xcol{x}$だとわかった。
この授業での微分はこういう($\xcol{\mathrm dx}$などを使う)方法で行っていく。高校などで見慣れたやり方とは違うかもしれないが、実際に自然科学で使うときはこっちの方が使いやすいのだ。
微分の練習
では、練習問題をやってみよう。
- $f(\xcol{x})=\xcol{x}^3$
- $f(\xcol{x})=\sin\xcol{x}$
- $f(\xcol{x})={1\over \xcol{x}}$
- $f(\xcol{x})=\cos\xcol{x}^2$
というわけで、しばらく互いに相談しつつ計算の時間を取った。
$f(\xcol{x})=\xcol{x}^3$は例と同様に、 $$ f(\xcol{x}+\xcol{\mathrm dx})=\underbrace{\xcol{x}^3}_{f(\xcol{x})}+\underbrace{3\xcol{x}^2}_{f'(\xcol{x})}\xcol{\mathrm dx}+\underbrace{+3\xcol{x}(\xcol{\mathrm dx})^2+(\xcol{\mathrm dx})^3}_{高次の微小量} $$ となり、$f'(\xcol{x})=3\xcol{x}^2$となる。
実は真面目に最後まで計算する必要はなくて、 $$ f(\xcol{x}+\xcol{\mathrm dx})=(\xcol{x}+\xcol{\mathrm dx})(\xcol{x}+\xcol{\mathrm dx})(\xcol{x}+\xcol{\mathrm dx}) $$ とみて、この中に$\xcol{x}^3$があること、$\xcol{x}^2\mathrm dx$が三つあること、までを読み取れば、 $$ f(\xcol{x}+\xcol{\mathrm dx})=\xcol{x}^3+3\xcol{x}^2+(高次の微小量) $$ とわかるから後は計算不要である(こういう省エネはどんどんやろう)。
なお、ここで行った二つの微分を図で表すこともできる。たとえば$\xcol{x}^2$の微分は
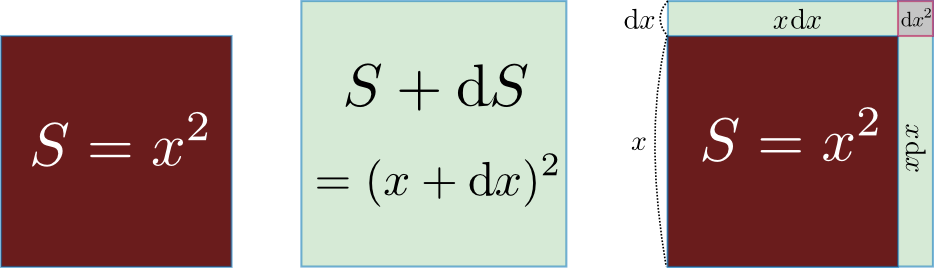
のように$(\xcol{\mathrm dx})^2$の部分を無視すればいい。
$\xcol{x}^3$の微分も、
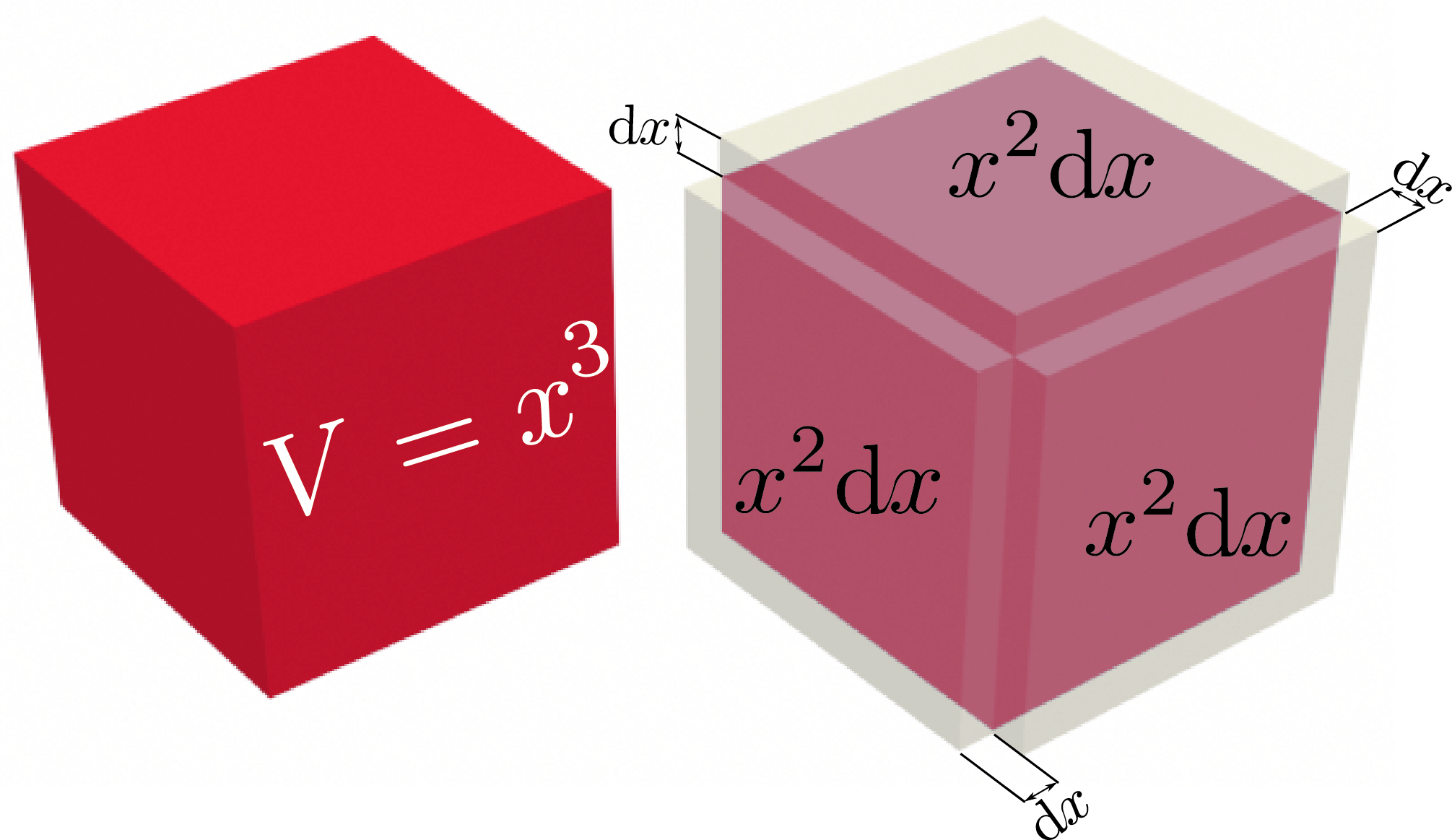
のような図で表現できる。係数3の意味が図からわかる。
次に$\sin\xcol{x}$の微分だが、これは三角関数の加法定理を使って、 $$ \sin(\xcol{x}+\xcol{\mathrm dx})=\sin\xcol{x}\cos\xcol{\mathrm dx}+\cos\xcol{x}\sin\xcol{\mathrm dx} $$ として、次に$\sin \xcol{x}\simeq \xcol{\mathrm dx},\cos\xcol{\mathrm dx}\simeq 1$を使うと、 $$ \sin(\xcol{x}+\xcol{\mathrm dx})=\sin\xcol{x}+\cos\xcol{x}\xcol{\mathrm dx} $$ となるから、$\sin\xcol{x}$の微分は$\cos\xcol{x}$とわかる(これも図解があるが、今日はやめておいた)。
時間の問題で後の問題は正解を授業でやらなかったのでここに書いておく。
${1\over \xcol{x}}$の微分は$-{1\over \xcol{x}^2}$。
$\cos\xcol{x}^2$の微分は$-2\xcol{x}\sin\xcol{x}^2$。
線形代数を勉強している人もいると思うけど、「線形」ってのは「1次式まで」ってことだから、随分しょぼい話をしているように思えるかもしれないけど、微分というのは「狭い範囲を考えて1次式までにして考える」という手法なので、微分でも線形代数はすごく役に立つのです。そういう話では、行列を微分したり積分したりもやることになります。
微分と積分
続いて積分とは何かについて少し説明したが、ここでは大事なところだけ書いておく。微分は「狭い範囲で考える」というものであった。自然現象を考えるとき、このような「狭い範囲を考える」(←ローカルな視点、という言い方をする)はとても大事である。しかし狭い範囲だけを考えていていいの?という心配をする人がいるかもしれない。その心配を吹き飛ばしてくれるのが、積分の存在である。積分は「微小な変化を足していく」ことで広い範囲で成立する式を作ることができるツールなのである。
微分という「狭い範囲での話」を積分を使って「広い範囲の話」に持ってくる、という操作の一例がこの後勉強する「微分方程式を解く」という計算なのだが、それについては来週からじっくりやろう。