熱伝導方程式
次の微分方程式(熱伝導方程式)は、1次元的な物体(細い棒など、断面積が無視できるような物体)の温度を表す関数の満たす微分方程式である。$\tau\kakko{\tcol{t},\xcol{x}}$は時刻$\tcol{t}$、場所$\xcol{x}$における温度を表す$\tau$はギリシャ文字の t に対応する文字で、読み方は「タウ」。温度(temperature)だから$t$を使いたいところだが、$t$は時間に使っているし、$T$も別の意味で使うのでギリシャ文字に登場願う。。
\begin{equation} \PDC{\tau(\tcol{t},\xcol{x})}{t}{\xcol{x}} =K\PPDC{\tau(\tcol{t},\xcol{x})}{\xcol{x}}{\tcol{t}}\label{dendou} \end{equation} この式にはどんな意味があるのかを図解しておこうこの本は数学が主題の本なので、熱伝導現象自体についての説明は簡単に留める。。右辺は$\xcol{x}$に関する二階微分である。二階微分はグラフの曲り具合という意味を持っていたことを思い出そう。すなわち($\tcol{t}$を一定として描いた)$\xcol{x}$-$\tau$グラフの曲がり具合である。

$\PPDC{\tau(\tcol{t},\xcol{x})}{\xcol{x}}{\tcol{t}}$が正ならそこで下に凸、負なら上に凸なグラフとなる。二階微分の意味を考えると、二階微分が負であるということは、「自分の両サイドの平均に比べて、自分の温度が低い」という状況を表している。このような時は温度は上がるだろう(二階微分が正であるときはこの逆)。温度変化が線形(グラフが直線)のときは温度が時間変化しない「温度が高い(温かい)方から流れてくる熱と、温度が低い(冷たい)方に奪われる熱が平衡している」という状況だと考えよう。流れてくる熱量が温度差に比例すると考えれば正しい。実際には流れてくる熱量はもっと複雑な関数であろうが、線形近似できる範囲では温度差に比例するとして差し支えない。。
変数分離による一般解
この式を変数分離で解く。すなわち、$\tau\kakko{\tcol{t},\xcol{x}}$をいきなり考えるのは難しいので、 \begin{equation} \tau\kakko{\tcol{t},\xcol{x}}=T\kakko{\tcol{t}}X\kakko{\xcol{x}} \end{equation} のように、$\tcol{t}$の関数の部分と$\xcol{x}$の関数の部分の積で表現されていると仮定し、これを代入してみると、 \begin{equation} \PDC{\left(T\kakko{\tcol{t}}X\kakko{\xcol{x}}\right)}{\tcol{t}}{\xcol{x}} =K\PPDC{\left(T\kakko{\tcol{t}}X\kakko{\xcol{x}}\right)}{\xcol{x}}{\tcol{t}} \end{equation} となる。左辺の$\tcol{t}$による微分は$T\kakko{\tcol{t}}$にだけ掛かり、右辺の$\xcol{x}$による微分は$X\kakko{\xcol{x}}$にだけ掛かる。結果を整理して左辺に$\tcol{t}$に関連する量が集まるようにする。 \begin{equation} \begin{array}{rll} X\kakko{\xcol{x}}{\ddt T}\kakko{\tcol{t}}=&K T\kakko{\tcol{t}}{\left(\ddx\right)^2 X}\kakko{\xcol{x}}\\[3mm] {\displaystyle{\ddt T}\kakko{\tcol{t}}\over T\kakko{\tcol{t}}}=&K {\displaystyle{\left(\ddx\right)^2 X}\kakko{\xcol{x}}\over X\kakko{\xcol{x}}} \end{array}\label{heatbunri} \end{equation}
ここで、左辺と右辺が定数$\alpha$になると考えて、 \begin{equation} {\displaystyle{\ddt T}\kakko{\tcol{t}}\over T\kakko{\tcol{t}}}=\alpha すなわち {\ddt T}\kakko{\tcol{t}}=\alpha T\kakko{\tcol{t}},~~~~ K {{\displaystyle \left(\ddx\right)^2 X}\kakko{\xcol{x}}\over X\kakko{\xcol{x}}}=\alpha すなわち {\left(\ddx\right)^2 X}\kakko{\xcol{x}}={\alpha\over K}X\kakko{\xcol{x}} \end{equation} の二つの常微分方程式を解けばよい。どちらも定数係数の線形斉次微分方程式だから、結果は \begin{equation} T\kakko{\tcol{t}}= A \E^{\alpha\tcol{t}},~~X\kakko{\xcol{x}}=\begin{cases}B \E^{\sqrt{{\alpha\over K}}\xcol{x}} +C \E^{-\sqrt{{\alpha\over K}}\xcol{x}}&\alpha\neq0のとき\\ D\xcol{x}+E& \alpha=0のとき\end{cases} \end{equation} であり$X$の方程式の方は$\alpha=0$の時に限り特性方程式が重解になるので別の解となる。、まとめると、 \begin{equation} \tau\kakko{\tcol{t},\xcol{x}}=\begin{cases} \E^{\alpha\tcol{t}}\left( F \E^{\sqrt{{\alpha\over K}}\xcol{x}} +G \E^{-\sqrt{{\alpha\over K}}\xcol{x}} \right)&\alpha\neq0のとき\\ {H\xcol{x}+J}&\alpha=0のとき \end{cases}\label{netsusolone} \end{equation} となる($AB=F,AC=G,AD=H,AE=J$と置いた)。様々な$\alpha$の値全てに対して一個ずつ解がある。
線形微分方程式なので、実際の解はいろんな$\alpha$の解に対する和であり、 \begin{equation} \tau\kakko{\tcol{t},\xcol{x}}= H\xcol{x}+J +\sum_{\alpha}\left( \E^{\alpha\tcol{t}}\left( F_\alpha \E^{\sqrt{{\alpha\over K}}\xcol{x}} +G_\alpha \E^{-\sqrt{{\alpha\over K}}\xcol{x}} \right)\right)\label{heatsolnobc} \end{equation} と書くことができる。係数$F,G$は各々の$\alpha$(ただし$\neq0$)の値に対して別々に存在するので、$F_\alpha,G_\alpha$と添字をつけて区別することにした。
$\sum_\alpha$は「$\alpha$の取り得る値それぞれについて和を計算する」という意味でこう書いたが、状況によっては$\alpha$は連続的に変化する数となる。その場合は和$\sum_\alpha$ではなく積分$\int\diff alpha$になる。
これで境界条件を指定しない場合の解を求めることができた。
$H,J,F_\alpha,G_\alpha$を決めるためには初期条件と境界条件が必要である。ここでは境界は$\xcol{x}=0$と$\xcol{x}=L$だとしよう。境界条件は考えている現象に応じて選ばなくてはいけない。ここでは、簡単な例として、境界で$\tau(t,0)=\tau(t,L)=0$という場合について解いてみよう。条件$\tau(t,0)=0$から \begin{equation} \tau\kakko{\tcol{t},\xcol{x}=0}= J +\sum_{\alpha}\left( \E^{\alpha\tcol{t}}\left( F_\alpha +G_\alpha \right)\right) \end{equation} となるがこれは$J=0$かつ(全ての$\alpha$に対して)$F_\alpha+G_\alpha=0$を意味する$\sum\E^{\alpha t}(F_\alpha+G_\alpha)=0$ではないのか?---と思う人がいるかもしれないが、任意の時間でこの和が0になるためには、係数$(F_\alpha+G_\alpha)$が全ての$\alpha$に対して0にならなくてはいけない。ので、 \begin{equation} \tau(\tcol{t},\xcol{x})=\sum_\alpha F_\alpha\E^{\alpha\tcol{t}}\left( \E^{\sqrt{{\alpha\over K}}\xcol{x}} -\E^{-\sqrt{{\alpha\over K}}\xcol{x}} \right)+H\xcol{x}\label{katahoukotei} \end{equation} という形になる。次に$\xcol{x}=L$での条件を考えると、 \begin{equation} \tau\kakko{\tcol{t},\xcol{x}=L}=\sum_\alpha F_\alpha\E^{\alpha\tcol{t}}\left( \E^{\sqrt{{\alpha\over K}}L} -\E^{-\sqrt{{\alpha\over K}}L} \right)+ HL=0\label{ryouhoukotei} \end{equation} となるが、任意の時刻で0になるためには、$H=0$かつ、全ての$\alpha$に対して \begin{equation} \E^{\sqrt{{\alpha\over K}}L} -\E^{-\sqrt{{\alpha\over K}}L}=0 \end{equation} となる必要がある。上の式を変形すると$\E^{2\sqrt{{\alpha\over K}}L}=1$である。\akantalk{$\E^0=1$だから$2\sqrt{{\alpha\over K}}L=0$}と考えてしまうと\akantalk{$\alpha=0$}だが、$\alpha=0$は$H\xcol{x}$の項ですでに別に考えているから不要である。実は$\ncol{n}$が整数のとき$\E^{2\ncol{n}\pi\I}=1$という式があるから、$\alpha$は0ではなく、 \begin{equation} 2\sqrt{{\alpha\over K}}L=2\ncol{n}\pi\I~~~すなわち、\alpha=-{\ncol{n}^2\pi^2 K\over L^2} \end{equation} のように決まる$\alpha$は連続的な量ではなく離散的な量である。こうなることを知っていたので、$\sum_\alpha$のように和を書いた。。この条件から$\sqrt{{\alpha\over K}}= \I{\ncol{n}\pi\over L}$として代入する「えっ、虚数にしていいの?」とびっくりする人がいるかもしれないが、この場合も、最終結果が実数になるように調整すれば別に問題はない。と、 \begin{equation} \tau\kakko{\tcol{t},\xcol{x}} =\sum_{\ncol{n}\neq0}\tilde F_\ncol{n} \E^{-{\ncol{n}^2\pi^2K\over L}\tcol{t}}\underbrace{\left( \E^{\I{\ncol{n}\pi\over L}\xcol{x}} -\E^{-\I{\ncol{n}\pi\over L}\xcol{x}} \right)}_{2\I\sin{\ncol{n}\pi\over L}\xcol{x}} =\sum_{\ncol{n}>0}\left(2\I \tilde F_\ncol{n}-2\I\tilde F_{-\ncol{n}}\right) \E^{-{\ncol{n}^2\pi^2 K\over L}\tcol{t}}\sin {\ncol{n}\pi\over L}\xcol{x}\label{twoiF} \end{equation} が境界条件を満たす一般解である。ここで、$\alpha$が$\ncol{n}^2\times(定数係数)$という形になったので、$F_\alpha$を$\tilde F_\ncol{n}$と書きなおした。
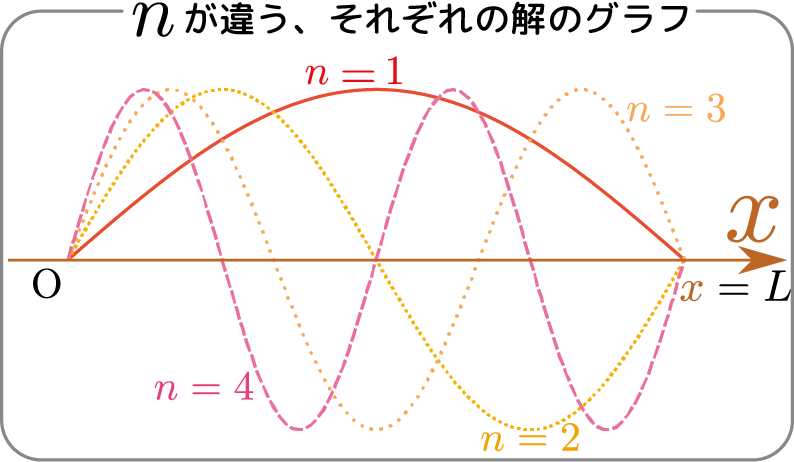
結果はさまざまな$\ncol{n}$に関する$\sin{\ncol{n}\pi\over L}\xcol{x}$に定数を掛けた項の和になっているが、$\sin$は奇関数で$\ncol{n}\to -\ncol{n}$と置き換えても本質的に同じ(符号が違うだけ)であるので、和を一つにまとめることにし、$\sum_{\ncol{n}>0}$とし、替りに$2\I \tilde F_\ncol{n}\to 2\I\tilde F_\ncol{n}-2\I\tilde F_{-\ncol{n}}$と置き換えた。以下、$2\I \tilde F_\ncol{n}-2\I\tilde F_{-\ncol{n}}=\tau_\ncol{n}$($\tau_\ncol{n}$は実数)と書こう。
微分方程式の解としては、初期条件も満たさなくてはいけない。$\tau\kakko{\tcol{t}=0,\xcol{x}}=\tau_初\kakko{\xcol{x}}$を初期条件とする($\tau_初\kakko{\xcol{x}}$は与えられた関数である)と、 \begin{equation} \tau_初\kakko{\xcol{x}}=\sum_{\ncol{n}>0}\tau_\ncol{n}\sin{\ncol{n}\pi\over L}\xcol{x} \end{equation} になるように係数$\tau_\ncol{n}$を決めればよい。
「係数$\tau_\ncol{n}$を選ぶことで任意の関数$\tau_初\kakko{\xcol{x}}$が表現できるのか?」というのは数学的には証明が必要なことである。もちろん証明はあり、今の境界条件$\xcol{x}=0$と$\xcol{x}=L$で0、を満たす連続な関数は上のように$\sin$の和で書くことができる。境界条件が違う時はまた別の関数($\cos$など)も使う。最初に「任意の関数は三角関数の和で表せる」と主張したのはフーリエで、ここで述べた熱伝導の方程式を考えていくうちに彼はこの結論に達した。この考え方が「フーリエ解析」という重要なテクニックへと発展する。
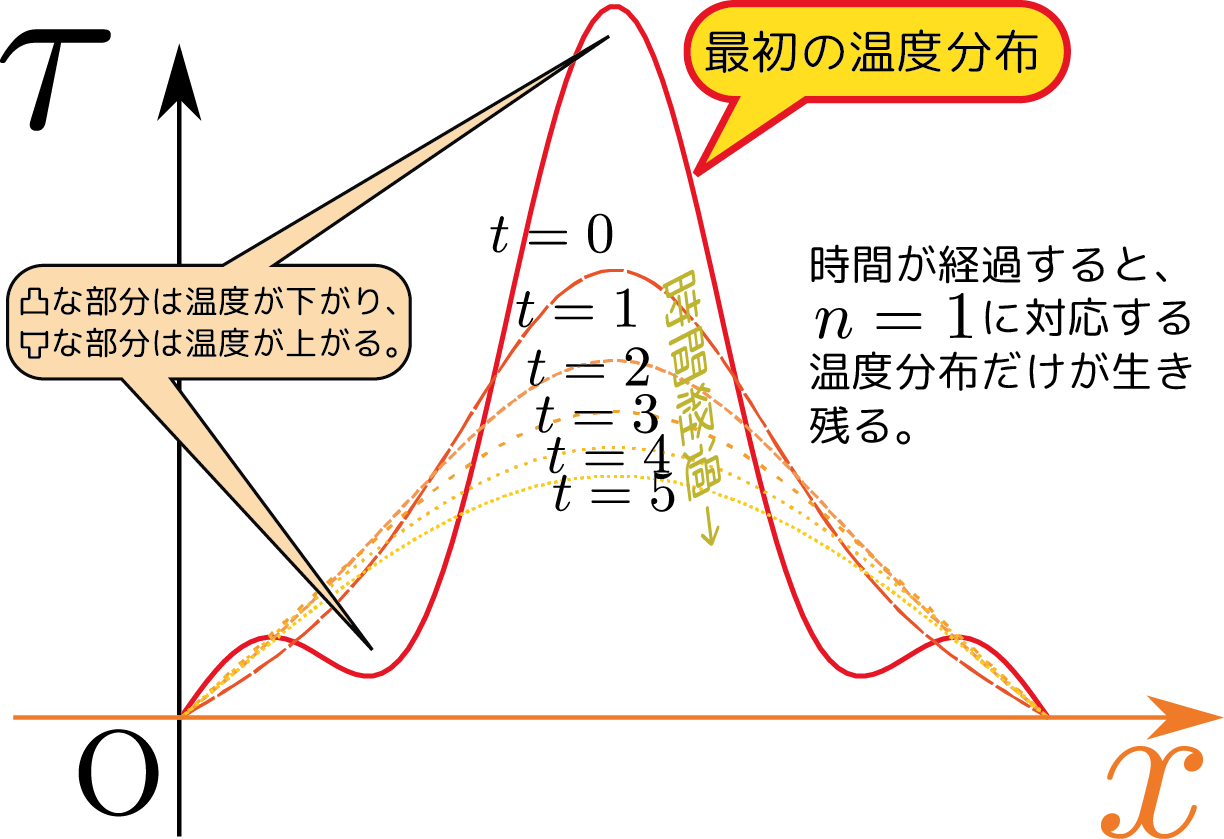
\begin{equation} \tau\kakko{\tcol{t},\xcol{x}}=\sum_{\ncol{n}>0}\tau_\ncol{n} \E^{-{\ncol{n}^2\pi^2 K\over L}\tcol{t}}\sin{\ncol{n}\pi\over L}\xcol{x} \end{equation} という式の物理的意味について考えておこう。この式には$\E^{-{\ncol{n}^2\pi^2K\over L}\tcol{t}}$がついているから、時間が立てば立つほど、温度は0に近づいていく。今考えている状況は両端が温度0で、他に熱源はないのだから、十分に時間経過すれば全体の温度が0になるというのは「もっとも」なことである。$\ncol{n}$の違いはグラフで書いた時の「波の数」なので、より短い波長の温度分布(つまり頻繁に寒暖が入れ替わっている)ときに「早く冷める」というのは感覚的にも納得できるだろう。
ここで、を見て偏微分方程式の解がどうなるかを実感してもらった。
また計算はやっていないが、の方も動きだけは見てもらった。