$\def\coldr{\rcol{\mathrm dr}}\def\coldvecx{\xcol{\mathrm d\vec x}}\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{~~~~~~~{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}\def\kidy{\opcol{\diff y}}\def\ve{\vec{\mathbf e}}\def\colvecx{\xcol{\vec x}}\definecolor{usuopcolor}{RGB}{237,234,203}\def\usuopcol#1{\color{usuopcolor}#1}\def\vgrad#1{{\usuopcol{\overrightarrow{\opcol{\rm grad}~\kuro{#1}}}}}\def\dX{\rcol{\mathrm dX}}\def\dY{\thetacol{\mathrm dY}}\def\opdf{\opcol{\mathrm df}}\def\coldf{\tcol{\mathrm df}}\def\dtwof{\opcol{\mathrm d^2f}}\def\murasakidb{\zcol{\mathrm d b}}\def\ao{\ycol}\def\aodV{\ycol{\diff V}}\def\aka{\xcol}\def\akadm{\xcol{\diff m}}\def\gunderbrace{\underbrace}$
今日の授業は前期の復習で、主に「微分ってなんだっけ?」を思い出してもらいました。
微分の定義について復習した後、$\ycol{y}=\xcol{x}^2$を微分する、という計算のやり方を復習した。
\begin{equation}
\begin{array}{rll}
\ycol{y}=&\xcol{x}^2&↓微小変化させる\\
\ycol{y}+\coldy=&\left(\xcol{x}+\coldx\right)^2&↓展開する\\
\ycol{y}+\coldy=&\xcol{x}^2+2\xcol{x}\coldx+\left(\coldx\right)^2&↓\ycol{y}=\xcol{x}^2を辺々引く\\
\coldy=&2\xcol{x}\coldx+\left(\coldx\right)^2&↓高次の微小量を消す\\
\coldy=&2\xcol{x}\coldx
\end{array}
\end{equation}
となって、これで微小量の比${\coldy\over\coldx}=2\xcol{x}$がわかる。
実際に微分積分を『使う』場面では、上のような「両辺の微小量を取る」という計算が結構大事。
同様に、$\ycol{y}=\xcol{x}^3$を計算すると、
\begin{equation}
\begin{array}{rll}
\ycol{y}+\coldy=&\left(\xcol{x}+\coldx\right)^3&↓展開する\\
\ycol{y}+\coldy=&\xcol{x}^3+3\xcol{x}^2\coldx+3\xcol{x}\left(\coldx\right)^2+\left(\coldx\right)^3&↓消せるものを消す\\
\coldy=&3\xcol{x}^2\coldx
\end{array}
\end{equation}
となるし、$\ycol{y}={1\over\xcol{x}}$の場合は、$\xcol{x}\ycol{y}=1$と修正してから、
\begin{equation}
\begin{array}{rll}
(\xcol{x}+\coldx)(\ycol{y}+\coldy)=&1\\
\xcol{x}\coldy + \ycol{y}\coldx =&0\\
\coldy = -{\ycol{y}\over\xcol{x}}\coldx = -{1\over\xcol{x}^2}\coldx
\end{array}
\end{equation}
となる。
この後、三角関数の微分を数式および図解で確認した。$\ycol{y}=\cos\xcol{x}$の微分は、数式で考えるならば
$$
\ycol{y}+\coldy = \cos\left(\xcol{x}+\coldx\right)
$$
を分解して、
$$
\ycol{y}+\coldy = \cos\xcol{x}\cos \coldx-\sin\xcol{x}\sin \coldx
$$
としたのち、極限を考えて$\cos \coldx=1,\sin \coldx = \coldx$を使う。ここで$\sin \coldx = \coldx$となる理由については
を見よ。
図で考える場合は、
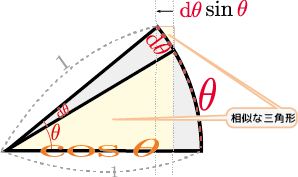
のように図を書いてやるとわかる。
本日は一回目で復習なので、内容は薄々だがいろいろと手を動かして計算のカンを取り戻してもらった。
