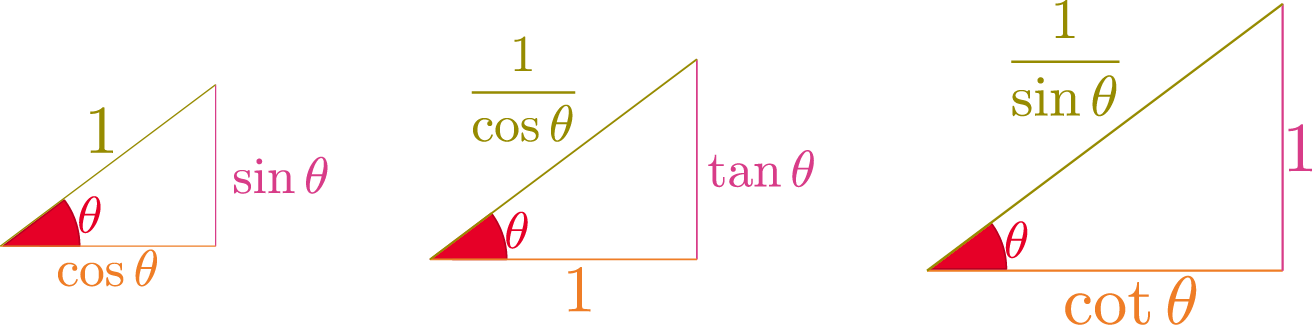三角関数

$\def\coldr{\rcol{\mathrm dr}}\def\coldvecx{\xcol{\mathrm d\vec x}}\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{~~~~~~~{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}\def\kidy{\opcol{\diff y}}\def\ve{\vec{\mathbf e}}\def\colvecx{\xcol{\vec x}}\definecolor{usuopcolor}{RGB}{237,234,203}\def\usuopcol#1{\color{usuopcolor}#1}\def\vgrad#1{{\usuopcol{\overrightarrow{\opcol{\rm grad}~\kuro{#1}}}}}\def\dX{\rcol{\mathrm dX}}\def\dY{\thetacol{\mathrm dY}}$

　今日はまず三角関数から。

　三角関数に関するアプリを

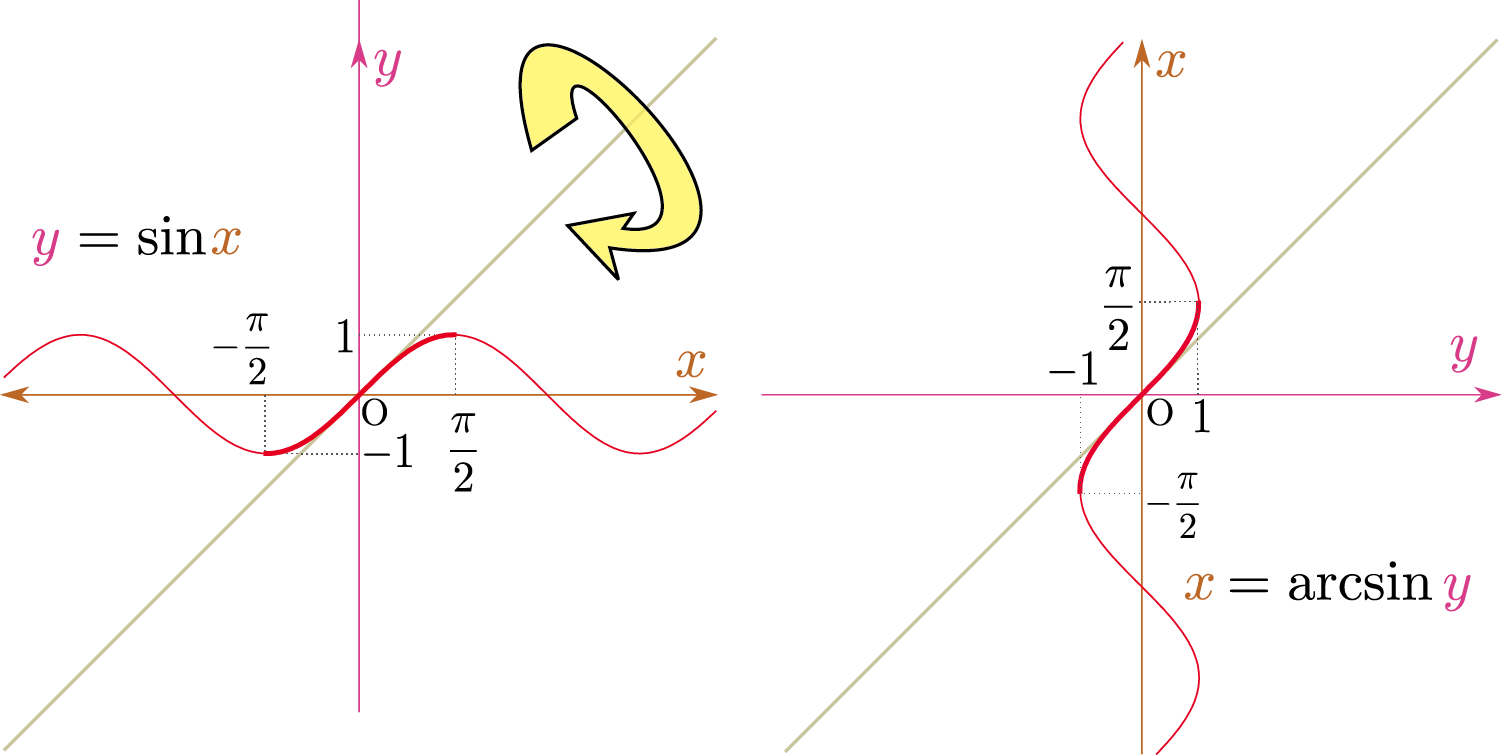
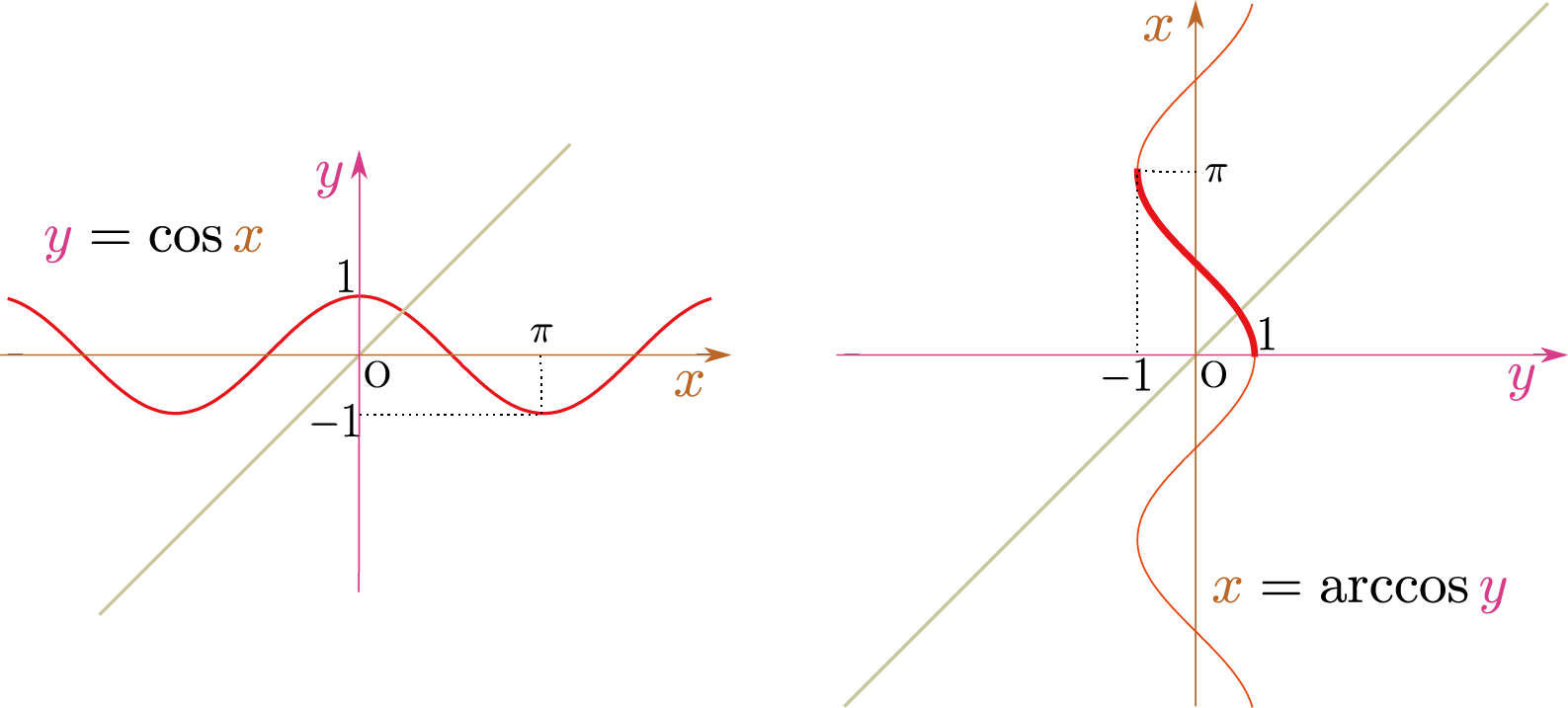
の順に使って遊びつつ、「三角関数とはなにか？」と互いの関係について考えた。

　三角関数の公式について、もう一つ。

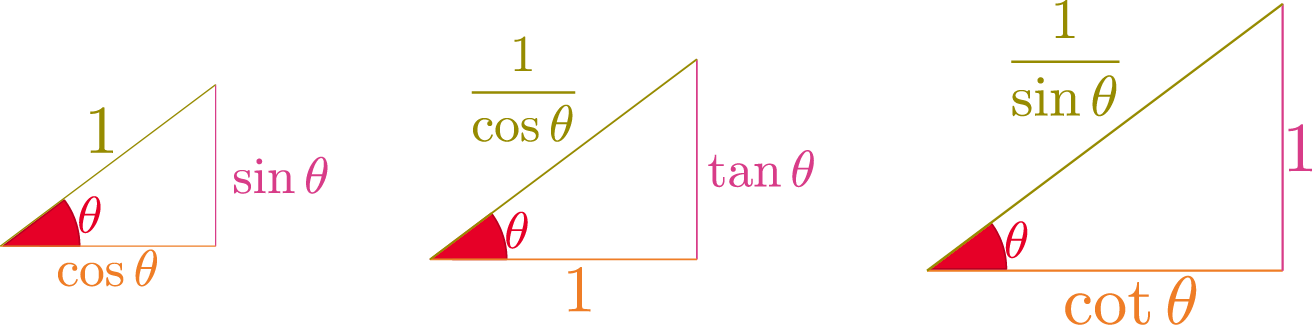
のような図に、三平方の定理（ピタゴラスの定理）すなわち$(\xcol{隣辺の長さ})^2+(\ycol{対辺の長さ})^2=(\opcol{斜辺の長さ})^2$を適用すると、それぞれの図に対応して以下の三つの式が導ける。 \begin{equation} \xcol{\cos^2{\theta}}+\ycol{\sin ^2{\theta}}=\opcol{1},~~ \xcol{1}+\ycol{\tan ^2{\theta}}=\opcol{{1\over \cos^2{\theta}}}=\opcol{\sec^2{\theta}},~~ \xcol{\cot^2{\theta}} +\ycol{1} =\opcol{{1\over\sin ^2{\theta}}}=\opcol{{\rm cosec}^2\,{\theta}} \end{equation}

こういう式を「新しい公式だ！」と単に覚えようとするのではなく、三平方のおなじみの「定理という式」の１つの変形である、という事実も含めて頭の中に（図と関連付けて）整理しておこう。バラバラに覚えた「公式」はすぐに忘れてしまうが、相互につながりを持って認識された知識は、なかなか忘れないし、身についたものとなり役に立つ。

　教科書の【問い】

をやってみると、

sin0.1=0.099833416646828

sin0.01=0.099833416646828

sin0.001=0.000999999833333

sin0.0001=0.000099999999833

のようになって、$sin\theta\simeq\theta$がわかる。なぜこうなるのかについてはまたあとで詳しくやろう。

合成関数と逆関数

　関数は「数$\to$数」の対応関係であるが、この対応関係を二段階にしたもの「数$\to$数$\to$数」を「合成関数」と呼ぶ。

　たとえば、部屋をクーラーで冷やしている。クーラーの電力を変えれば温度が変わる（電力→温度）。そして、温度が変わればその気体中の音速が変わる（温度→音速）。こうすると「電力を変えれば（温度の変化を通じて）音速が変わる」（電力→温度→音速）という関数関係ができる（こういう例を自分でも考えてみよう）。

　合成関数の例を数式で考えよう。$\ycol{y}=1-\xcol{x}^2$という$\xcol{x}\to \ycol{y}$という対応関係があり、さらに$\zcol{z}=\sqrt{\ycol{y}}$という$\ycol{y}\to \zcol{z}$の対応関係があれば、この二つをまとめて、$\zcol{z}=\sqrt{1-\xcol{x}^2}$という$\xcol{x}\to\zcol{z}$の「合成関数」を作ることができる。二つの関数を$\ycol{y}=f\kakko{\xcol{x}}$（$\ycol{y}$が$\xcol{x}$の関数である）および$\zcol{z}=g\kakko{\ycol{y}}$（$\zcol{z}$が$\ycol{y}$の関数である）と書けば、合成関数は$\zcol{z}=g\kakko{f\kakko{\xcol{x}}}$のように書ける。

　ここで、

のアプリを使ったが、androidの調子がよくなかったので各自で遊ぶのではなくプロジェクタで画像を見せて説明した。

逆関数

　$\xcol{x}\to\ycol{y}$という対応に対してこの逆の$\ycol{y}\to\xcol{x}$という対応を元の関数の「逆関数」と呼ぶ。$\ycol{y}=f\kakko{\xcol{x}}$の逆関数は$\xcol{x}=f^{-1}\kakko{\ycol{y}}$と表記する。$f^{-1}\kakko{\xcol{x}}$は$\left(f\kakko{\xcol{x}}\right)^{-1}={1\over f\kakko{\xcol{x}}}$とは違うので注意。$f^{-1}$は「えふいんばーす」と読む。

　逆関数を考えるときにも定義域と値域に対する注意は必要である。たとえば、「$\ycol{y}=\xcol{x}^2$という関数の逆関数は$\xcol{x}=\sqrt{\ycol{y}}$」と言いたくなるが、これは$\xcol{x}\geq0$という範囲で考えないと正しくない。また、$\ycol{y}=\sin{\xcol{x}}$の逆関数は$\xcol{x}=\arcsin \ycol{y}$$\arcsin$は「アークサイン」と読む。arcの意味は「弧」。扇型の弧の長さ（ラジアンを使っているから、単位円であれば角度$\theta$と同じ）を求める関数、という意味で「arc」をつける。と書く同じ関数を$\xcol{x}=\sin^{-1}\ycol{y}$と書くこともあるが、これは$\xcol{x}={1\over \sin\ycol{y}}$という意味ではないので間違えないように（$\sin$と混同しないように$\sin$の頭文字を大文字に変えて$\xcol{x}={\rm Sin}^{-1}\ycol{y}$のように書く場合もある）。が、$\xcol{x}=\arcsin \ycol{y}$の$\ycol{y}$は$-1\leq\ycol{y}\leq1$の範囲になくてはいけない（こう書いたときには$\ycol{y}$は独立変数なので、この範囲は「定義域」である）。

　逆関数を考えるときには、関数が1対1対応かどうかに気をつけよう。たとえば$\ycol{y}={\xcol{x}^2}$は1対1ではない。$\xcol{x}=1$でも$\xcol{x}=-1$でも$\ycol{y}=1$になってしまうから、$\xcol{x}$二つと$\ycol{y}$一つが対応している（$\xcol{x}=0$を除く）。この場合、$\xcol{x}\to \ycol{y}$は関数であるが、$\ycol{y}\to\xcol{x}$は関数ではない。関数にするには定義域を制限するか、代表を一つ取り出すことで$\ycol{y}$と$\xcol{x}$が1対1対応になるようにする。$\ycol{y}={\xcol{x}^2}$の場合であれば、$\xcol{x}\geq 0$の範囲しか考えないことにすればよい。

　より深刻な「1対1対応でない例」として$\ycol{y}=\sin{\xcol{x}}$の逆関数$\xcol{x}=\arcsin \ycol{y}$を見よう。

　$\ycol{y}=\sin{\xcol{x}}$は$\xcol{x}$に$\xcol{x}+2n\pi$（$n$は整数）を代入しても値が変わらない。このため、$\ycol{y}$一つ（ただし、$-1\leq \ycol{y}\leq 1$）に対して無限個の$\xcol{x}$が対応してしまう。

　独立変数を横軸、従属変数を縦軸にするという慣習に従ってグラフを描く場合、関数と逆関数のグラフの関係は上の図に示したように「$\ycol{y}=\xcol{x}$の線、つまり斜め45度$\left({\pi\over 4}\right)$の線を対称線にして反転させる」ことで得られる（元の関数と逆関数では独立変数と従属変数の役割が入れ替わるから）。しかしこのままでは、$\xcol{x}=\arcsin\ycol{y}$の方が関数になっていない。一つの$\ycol{y}$に対し$\xcol{x}$がたくさんあるからである。そこでグラフのうち太い線にした部分$-{\pi\over 2}\leq \xcol{x}\leq {\pi\over 2}$だけを取り出して、残りは捨てることにする。結果、$\xcol{x}=\arcsin\ycol{y}$の定義域は$-1\leq \ycol{y} \leq 1$、値域は$-{\pi\over 2}\leq \xcol{x}\leq {\pi\over 2}$となる（これで一つの$\ycol{y}$に対して一つの$\xcol{x}$が対応する）。この二つの関数を合成すると何もしない関数$\xcol{x}=\xcol{x}$になると期待するが、そうはいかない。

　$\ycol{y}=\cos\xcol{x}$の逆関数は$\xcol{x}=\arccos\ycol{y}$である（$\arccos$は「アークコサイン」と読む）。こちらも変数の範囲に注意が必要だが、ここではグラフだけを載せておこう。

　$\ycol{y}=\arccos \xcol{x}$の定義域は$-1\leq\xcol{x}\leq 1$、値域は$0\leq \ycol{y} \leq \pi$にすることが多い。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。