3次元面積分と体積積分
外積の復習
3次元の場合外積はベクトルだが、その向きをまずは図形で表現しよう。二つのベクトルがある面上にあるとする。外積の結果はその平面の法線方向を向く。
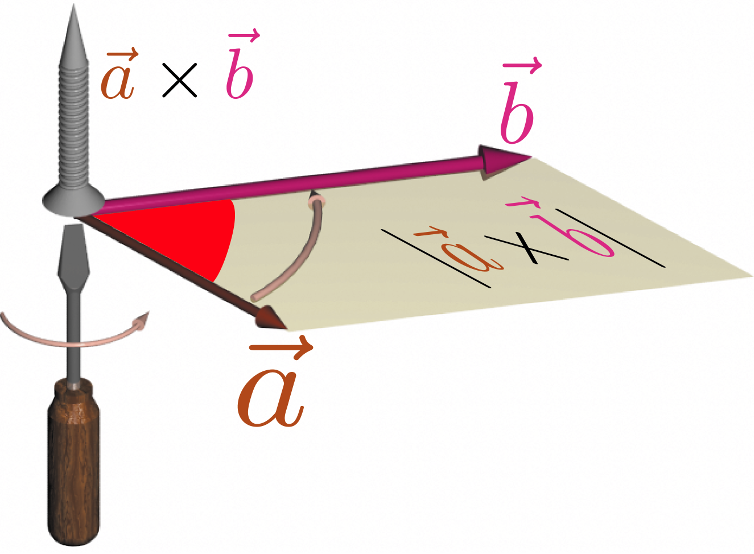
「法線」というだけでは向きがわからないが、図に示したように「$\vec a$の向きから$\vec b$の向きへとベクトルを回したとき、右ネジが進む向きを「$\vec a\times \vec b$の向き」とする。
外積という計算の結果であるベクトルの方向は「回転の軸」の方向である。「どの方向からどの方向へ回すか」の例として、三つの座標軸$x,y,z$から二つを選んで、図を描いてみよう。
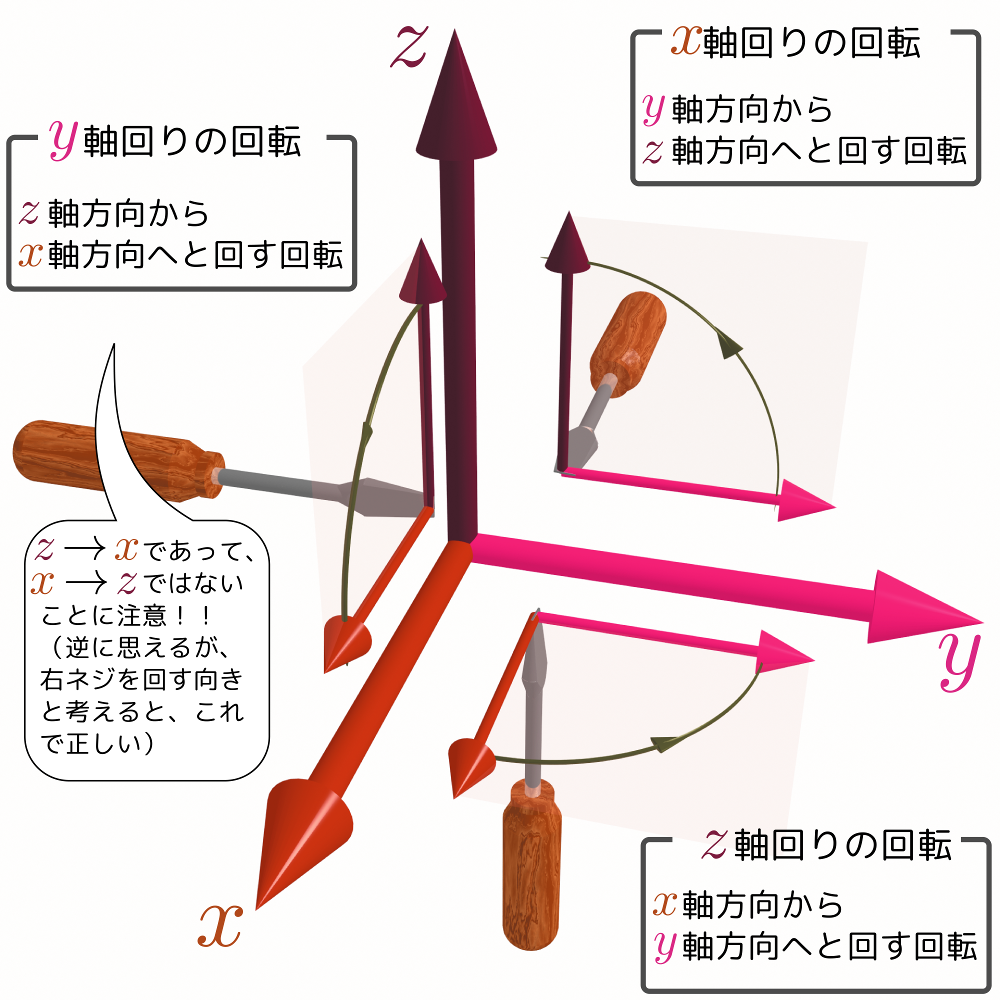
「$x$軸方向から$y$軸方向へ回す」という回転を「$z$軸まわりの回転」と表現した(その意味は図に描き込んだように$z$軸の方向にドライバーを向けてネジを締めるように回すというイメージで理解してほしい)。
図中にも書いたが、$y$軸まわりの回転は「$x$軸方向から$z$軸方向」ではなく「$z$軸方向から$x$軸方向」であることにも注意しよう。
二つのベクトルの外積の大きさは、 \begin{equation} |\xcol{\vec a}\times \ycol{\vec b}|=|\xcol{\vec a}||\ycol{\vec b}||\sin\theta| \end{equation} で表現される。$\theta$は二つのベクトルの成す角である。
$|\xcol{\vec a}\times\ycol{\vec b}|$の図形的(幾何学的)意味は図の平行四辺形の面積である。あるいは$\ycol{\vec b}$を$\xcol{\vec a}$に並行な成分$\ycol{\vec b}_\parallel$と、$\xcol{\vec a}$に垂直な成分$\ycol{\vec b}_{\bot}$に分けて($\xcol{\vec a}$と$\ycol{\vec b}$の役割は逆でも可)、 \begin{equation} |\xcol{\vec a}\times \ycol{\vec b}|=|\xcol{\vec a}||\ycol{\vec b}_\bot|=|\xcol{\vec a}_\bot||\ycol{\vec b}|\label{kieruheikou} \end{equation} という計算をしていると思ってもよい(これは横が$|\xcol{\vec a}|$で縦が$|\ycol{\vec b}_{\bot}|$の長方形の面積でもある)。
同じ方向を向いているベクトルどうしの外積は0である。平行四辺形の面積という意味を考えれば、「同じ方向を向いている2本のベクトルの作る面積は0」ということから納得できる(数式で考えるならば$\theta=0$である)。特に$\xcol{\vec a}\times\ycol{\vec b}=0$であっても$\xcol{\vec a}$も$\ycol{\vec b}$も零ベクトルでない場合があることには注意しよう。
外積の交換・結合・分配法則
$\xcol{\vec a}\times \ycol{\vec b}$は「$\xcol{\vec a}$というベクトルを$\ycol{\vec b}$の向きを向くように回すときの軸の向き」なのに対し、$\ycol{\vec b}\times \xcol{\vec a}$はその逆で「$\ycol{\vec b}$というベクトルを$\xcol{\vec a}$の向きを向くように回すときの軸の向き」であり、この二つは逆である。しかし、平行四辺形の面積には違いがないので、絶対値は等しい。よって、 \begin{equation} \xcol{\vec a}\times\ycol{\vec b}= - \ycol{\vec b}\times \xcol{\vec a}\label{gaisekikoukan} \end{equation} が成立する(外積の定義には$\sin \theta$が含まれているが、\文中式{$\sin (-\theta)=-\sin \theta$}からも以上のことはわかる)。3次元では外積の結果のベクトルが逆を向く。
3次元の外積でも結合法則は成り立たない。例を一つ挙げておこう法則が成り立つことを示すときは一つの成り立つ例を出してもダメ(他に成り立たない場合があるかもしれない)であるが、成り立たないことを示すのなら、成り立たない例が一つあればそれで十分。。 \begin{equation} \ve_x \times(\ve_y\times\ve_y)=0 \end{equation} である(括弧の中の$\ve_y\times\ve_y$が0だから)。一方、 \begin{equation} (\gunderbrace{\ve_x \times\ve_y}_{=\ve_z})\times\ve_y=\ve_z \times \ve_y = -\ve_x \end{equation} となって0ではない。
分配法則は、外積についても成立する。式で書くと \begin{equation} \zcol{\vec a}\times(\xcol{\vec b}+\ycol{\vec c})=\zcol{\vec a}\times\xcol{\vec b}+\zcol{\vec a}\times \ycol{\vec c}\label{gaisekibunpai} \end{equation} である。証明は教科書の付録参照。
3次元空間内の面積
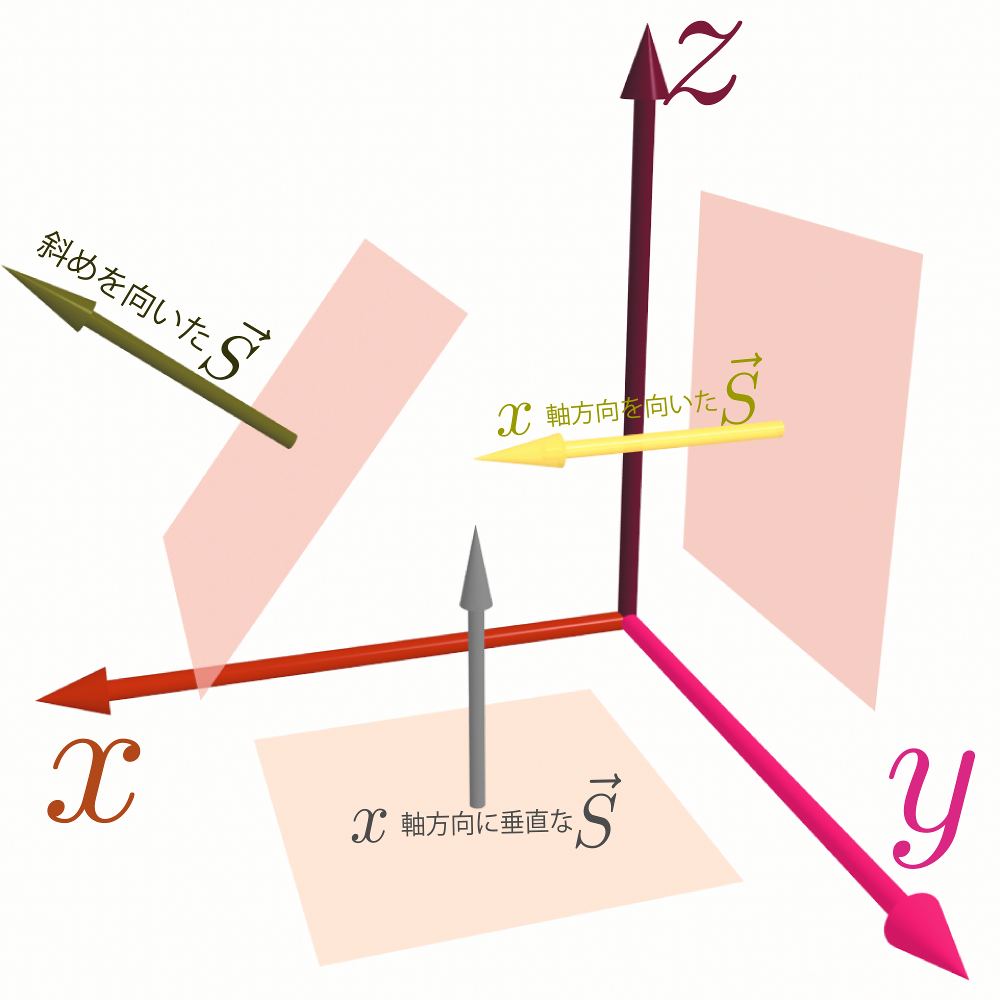
3次元の中にある面積はベクトルで表現されると言うとビックリされることが多い。
面積ベクトルは、大きさ(ベクトルの長さ)として面積の絶対値を持ち、向きはその法線方向面積に対し垂直なベクトルを「法線ベクトル」と呼ぶ。その方向が「法線方向」である。を向く。法線方向と言われても向きは二つあるが、「裏」と考えている面から「表」と考えている面へと向かう方向へと取るのが普通である(どっちを「裏」と考えるかは文脈による)。
そんなことして何の役に立つの?と思うかもしれないが、面積をベクトルとして考えることには大きなメリットがたくさんあり、だからこそ使われているのである。
たとえば、風車を作るとしよう。風が$\xcol{x}$方向に吹いているとすれば、その風を受けるためには$\ycol{y}$-$\zcol{z}$面に平行な面積、つまり(面積ベクトルが$\xcol{x}$方向を向いた面積)をもってこなくてはいけない。斜めに風を受けるとその分損をすることになる。このような意味で、空間内にある面積においては、「向き」という情報も重要である。
と、テキストには書いておいたが、授業では「太陽電池パネルを設置するときに、どの角度で設置すると太陽のエネルギーをどの程度受けられるか」という問題を考えるときに有用、という話もした。
具体的に、面積が$\vec S$で表現され、空気が速度$\vec v$で通り過ぎていくとき、この面積を通り抜ける空気の体積は単位時間あたり$\vec v\cdot\vec S$である(面積ベクトルと速度ベクトルが平行だとこの量は正つまり「裏」と考えた方から「表」と考えた方へ抜けるときに正。になり、垂直ならば0になる)。このように「ある面積を通り抜ける流れ(flux)を考える」というとき、流れのベクトルと面積のベクトルの内積を取るという操作が必要になってくる。そのとき、「向きのある面積」が重要になるのである。
まず$\xcol{x}$-$\ycol{y}$平面上に存在する微小な長方形の面積を式で表現するところから始めよう。$\xcol{x}$方向に$\coldx$の、$\ycol{y}$方向に$\coldy$の幅を持つ長方形の面積は、ベクトル$\coldx\ve_x$とベクトル$\coldy\ve_y$の外積 \begin{equation} \coldx\ve_x\times \coldy\ve_y=\coldx\coldy\ve_z \end{equation} で表される。$\zcol{z}$方向を向いて大きさ$\coldx\coldy$(これが微小長方形の面積)のベクトルである。同様のことを$\ycol{y}$-$\zcol{z}$平面と$\zcol{z}$-$\xcol{x}$平面でも考えることができる。
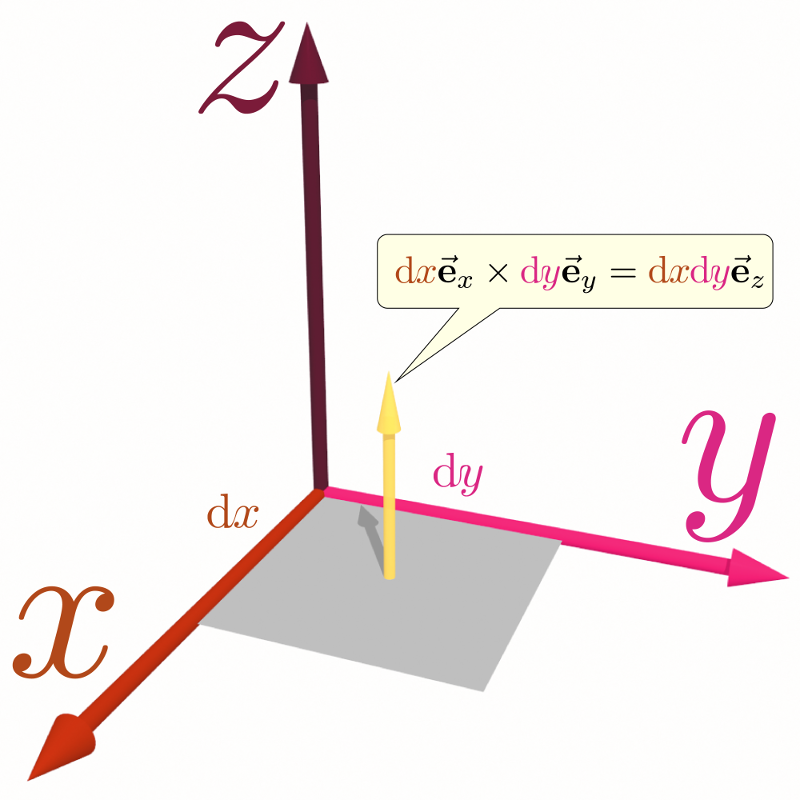
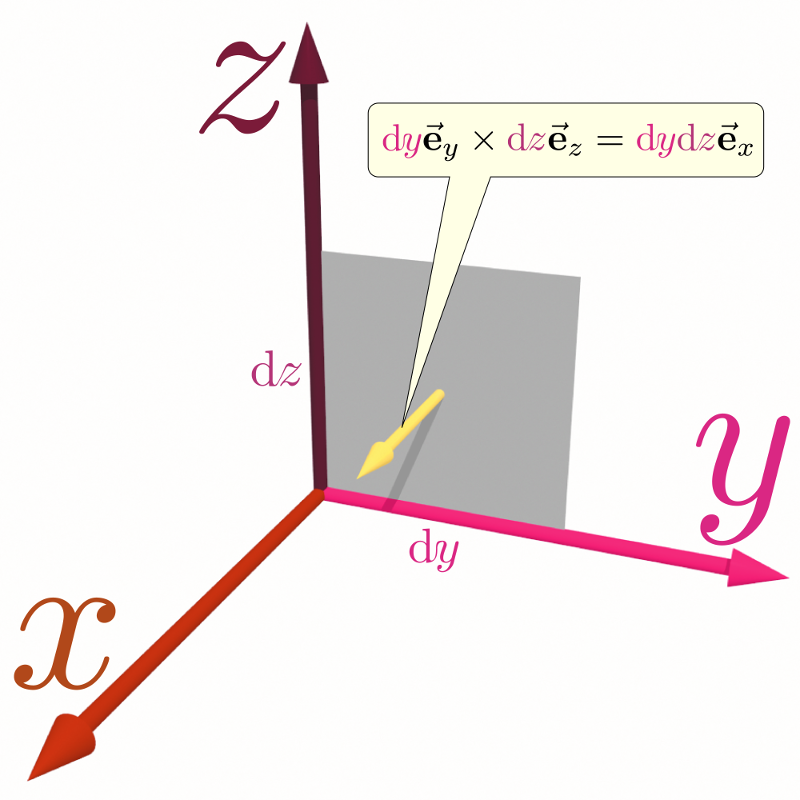
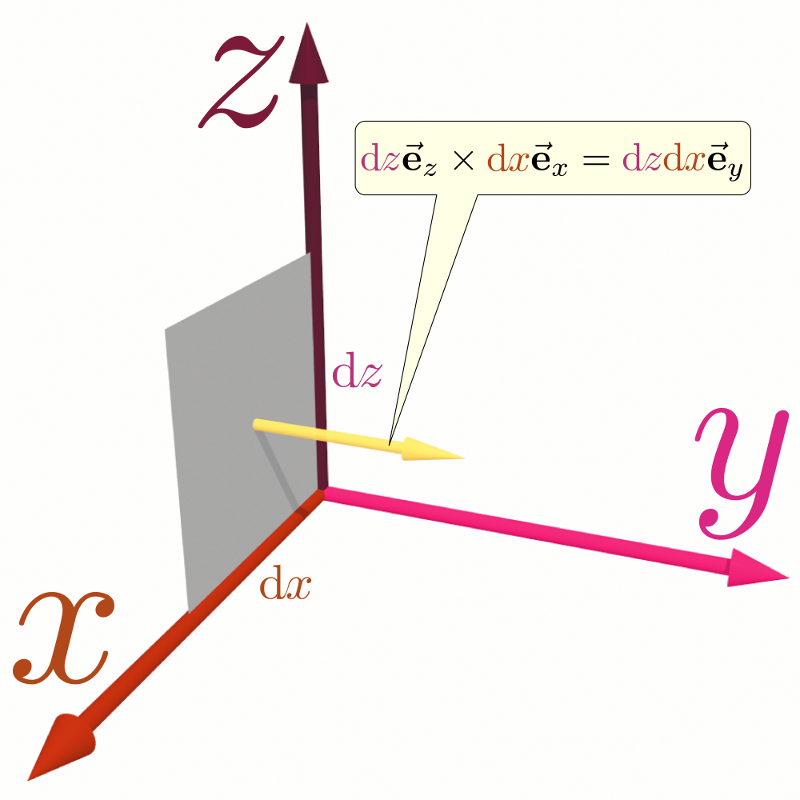
同様に、$\ycol{y}$-$\zcol{z}$平面における面積は$\xcol{x}$方向を向いたベクトル$\coldy\ve_y\times \coldz\ve_z=\coldy\coldz\ve_x $で、$\zcol{z}$-$\xcol{x}$平面における面積は$\ycol{y}$方向を向いたベクトル$\coldz\ve_z\times \coldx\ve_x=\coldz\coldx\ve_y$で表現されることになる。
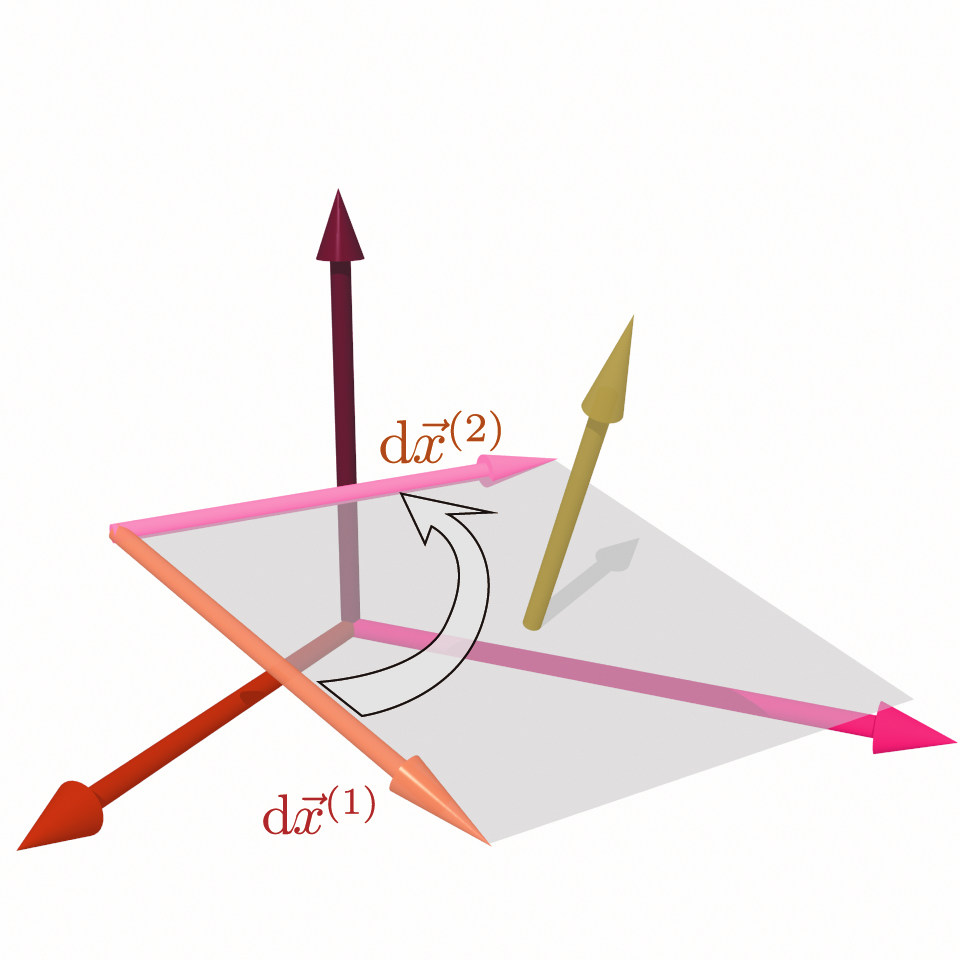
以上のように、3次元の微小面積は$\coldvecx^{(i)}=\xcol{\coldx^{(i)}}\ve_x+\ycol{\coldy^{(i)}}\ve_y+\zcol{\coldz^{(i)}}\ve_z$($i=1,2$)のような二つの微小変位ベクトルを使って \begin{equation} \begin{array}{rl} \coldvecx^{(1)}\times\coldvecx^{(2)}=& \left( \ycol{\coldy^{(1)}} \zcol{\coldz^{(2)}} - \zcol{\coldz^{(1)}} \ycol{\coldy^{(2)}} \right)\ve_x\\ +& \left( \zcol{\coldz^{(1)}} \xcol{\coldx^{(2)}} - \xcol{\coldx^{(1)}} \zcol{\coldz^{(2)}} \right)\ve_y\\ +& \left( \xcol{\coldx^{(1)}} \ycol{\coldy^{(2)}} - \ycol{\coldy^{(1)}} \xcol{\coldx^{(2)}} \right)\ve_z\end{array} \end{equation} のように書かれる。外積なのは2次元の面積の式と同じだが、3次元では外積がベクトルになる。
ベクトルとなると足算もベクトル的に行う必要があるのだが、この「面積のベクトル和」はとても便利なものである。それを示すために、三角錐の四つの面における面積ベクトル$\vec S_1,\vec S_2,\vec S_3,\vec S_4$を考えよう。面積ベクトル$\vec S_i$は三角錐から外へ出る向きに($\vec S_1$は$\xcol{x}$軸負の向きに、$\vec S_2$は$\ycol{y}$軸負の向きに、$\vec S_3$は$\zcol{z}$軸負の向きになるように)定義してある。$\vec S_4$は図からもわかるようにどの軸にも沿っていない、斜めの方向を向く。
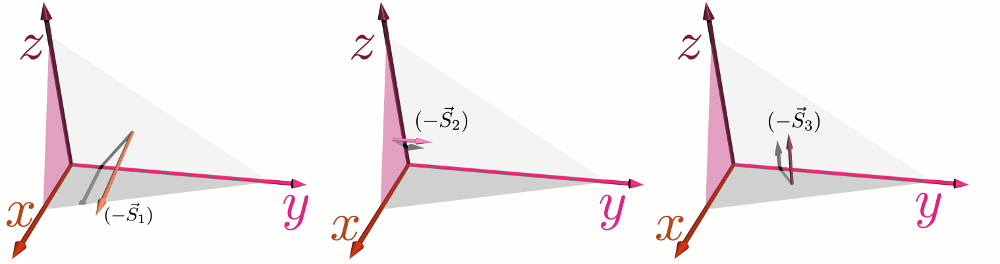
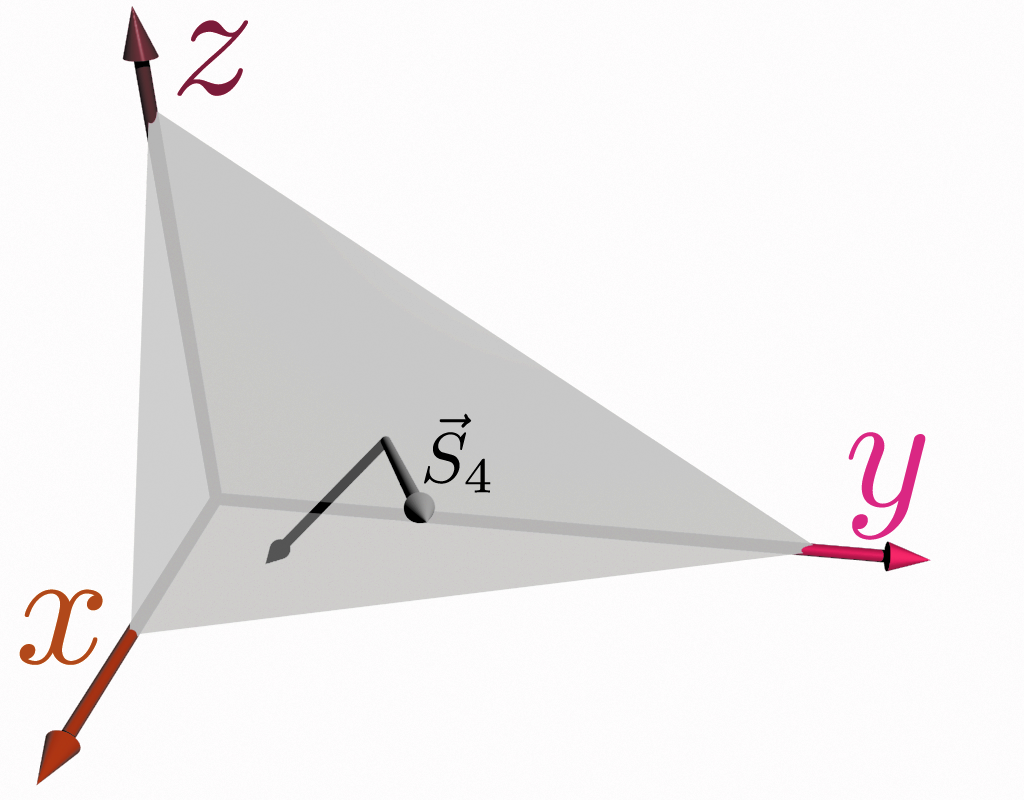
四つめの面の面積ベクトル$\vec S_4$はこれら三つの面積ベクトル$(-\vec S_1),(-\vec S_2),(-\vec S_3)$の和になっている。すなわち、外に出て行くベクトルに関して$\vec S_1+\vec S_2+\vec S_3+\vec S_4=0$が言える。実は三角錐に限らず一般の閉曲面で、面積ベクトルを足していくと0になることが言える。微小三角錐はそのことを示す最も単純な例である。
面積ベクトルは面に垂直で面積に比例する。これは静水(流れがない水)中にある物体が水から受ける圧力(水圧)の総和と同じ性質である。ただし面積ベクトルは外側向きに定義しているので、水圧と向きは反対になる。面積ベクトルは各面に掛かる水圧の総和の力に(向きが逆なので負の比例係数で)比例する。静水中に置かれた物体に働く力はつりあうはずなのでその和は0になることが納得できる流れがない水中に沈められた物体が水から力を受けてひとりでに動き出すことはありそうにないことである。現実の水圧は深いほど強いが、重力の効果はここでは無視する。無視しない場合は水圧の総和は浮力になる。
三角錐の面積ベクトルの和が0になることは上で述べたような「水圧による力のつりあい」で考えても理解できるし、下の図のように三つのベクトル$\xcol{\vec a},\ycol{\vec b},\zcol{\vec c}$を使って表現することでも証明できる。
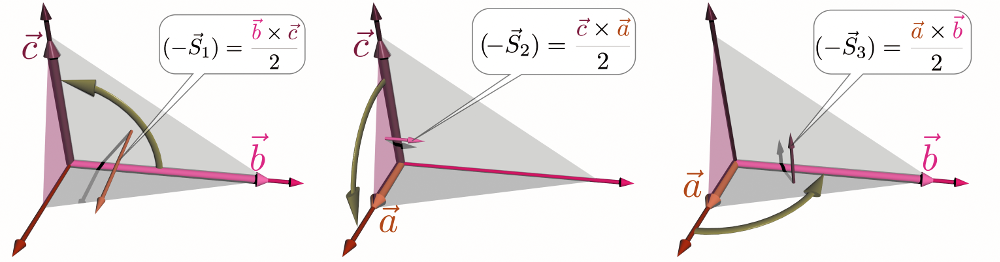
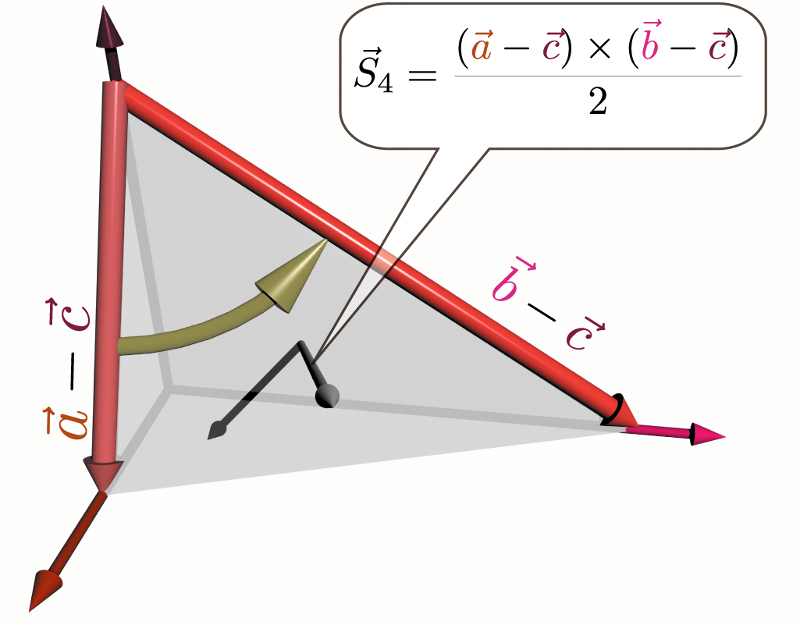
三角錐のうち三つの面はそれぞれ図に示したような面積ベクトルを持つ(平行四辺形の半分なので2で割った)。
一方、最後の面の面積ベクトル$\vec S_4$は \begin{align} \vec S_4 =& {1\over 2}\left((\xcol{\vec a}-\zcol{\vec c})\times(\ycol{\vec b}-\zcol{\vec c})\right) ={1\over 2}\left(\xcol{\vec a}\times \ycol{\vec b}-\xcol{\vec a}\times\zcol{\vec c}-\zcol{\vec c}\times\ycol{\vec b}\right)\nonumber\\[3mm] =& \gunderbrace{{1\over 2}(\xcol{\vec a}\times\ycol{\vec b})}_{(-\vec S_3)} +\gunderbrace{{1\over 2}(\zcol{\vec c}\times\xcol{\vec a})}_{(-\vec S_2)} +\gunderbrace{{1\over 2}(\ycol{\vec b}\times\zcol{\vec c})}_{(-\vec S_1)} \end{align} のようにベクトル計算され、こちらからも面積ベクトルの足算の意味が理解できる。この導出方法から、$\vec S_1+\vec S_2+\vec S_3+\vec S_4=0$は閉じた四面体なら成立する(もっと複雑な形についても同様)。
球の表面の面積要素

3次元空間の中の球の場合、極座標の$\thetacol{\theta}$と$\phicol{\phi}$を使う。すると面積要素は \begin{equation} \diff \vec S=\goverbrace{\rcol{r}\ve_\theta}^{\tiny\PDC{\vec x\,\kakko{\rcol{r},\thetacol{\theta},\phicol{\phi}}}{\thetacol{\theta}}{\rcol{r},\phicol{\phi}}}\coldtheta\times\goverbrace{\rcol{r}\sin\thetacol{\theta}\ve_\phi}^{\tiny\PDC{\vec x\,\kakko{\rcol{r},\thetacol{\theta},\phicol{\phi}}}{\phicol{\phi}}{\rcol{r},\thetacol{\theta}}}\coldphi =\rcol{r}^2\sin \thetacol{\theta}\coldtheta\coldphi\ve_r \end{equation} となる。面積ベクトルの絶対値を積分 \begin{equation} \int_0^\pi\coldtheta\int_0^{2\pi}\coldphi \rcol{r}^2 \sin \thetacol{\theta}=4\pi \rcol{r}^2 \end{equation} を行うと球の表面積が出てくる。
面積だけを計算したのでは面積をベクトルにしたことの恩恵が感じられないので、前に述べた}「通り抜ける空気の量」を計算してみよう(太陽光線のエネルギーでもよい)。すぐ上で考えた球体のある場所に、速度が$v\ve_x$で表される風が吹いていたとすると、面積要素を単位時間あたりに通り抜ける空気の量は \begin{equation} v\ve_x\cdot\rcol{r}^2\sin \thetacol{\theta}\coldtheta\coldphi\ve_r \end{equation} であるが、$\ve_x\cdot\ve_r=\sin \thetacol{\theta}\cos\phicol{\phi}$であるから、 \begin{equation} v \int_0^\pi\coldtheta\int_0^{2\pi}\coldphi \rcol{r}^2 \sin \thetacol{\theta}\times\sin \thetacol{\theta}\cos\phicol{\phi} \end{equation} という積分を行えばよい。結果は$\phicol{\phi}$積分の$\int_0^{2\pi}\coldphi\cos\phicol{\phi}=0$のおかげで0になる。
理由は単純で、球の表側と裏側で逆向きに通り抜けるので、それぞれの正負で消し合うからである。 そこで、今度は$\ve_x$方向の風を受ける部分だけで計算してみると、 \begin{equation} v\int_0^\pi\coldtheta\int_{{\pi\over 2}}^{{3\pi\over 2}}\coldphi \rcol{r}^2 \sin \thetacol{\theta}\times\sin \thetacol{\theta}\cos\phicol{\phi} \end{equation} となる。今度は積分の結果は \begin{equation} v\rcol{r}^2 \gunderbrace{\int_0^\pi \sin^2 \thetacol{\theta}\coldtheta}_{{\pi\over 2}}\gunderbrace{\int_{\pi\over 2}^{3\pi\over 2}\cos\phicol{\phi}\coldphi}_{-2} =-v\pi\rcol{r}^2 \end{equation} となる。これは実は球の断面積$\times(-v)$である。