波動論2006年度講義録第７回


←第6回へ　目次に戻る


　前回は行列の固有値を出すところまでやった。その復習の後、以下が続きで ある。
　この固有値が出れば、方程式がm[(d2X)/(dt2)]=−kXとm[(d2Y)/(dt2)] =−3kYになることはわかってしまう。あと求めるべきは固有ベクトルであるが、それも簡単で、λの値を代入すると、
λ = −kの時、(M−λI)= (
−k
k
k
−k
)      λ = −3kの時、(M−λI)= (
k
k
k
k
)
(3.43)
なので、この行列をかけて0になるということは、
λ = −kの時、固有ベクトル (
1
1
)      λ = −3kの時、固有ベクトル (
1
−1
)
(3.44)
とわかる。ここでベクトルの「規格化(normalization)」を行う。規格化とは「長さを1にすること」である。今のままだと
(
1
1
)
というベクトルは長さが√[(12+12)]=√2となる。そこでこれを√2で割って長さを1にする。 λ = −3kに対しても同様に規格化して、
λ = −kの時、固有ベクトル (

1
√2

1
√2
)      λ = −3kの時、固有ベクトル (

1
√2
− 1
√2
)
(3.45)
とする。Tは、今作った二つの列ベクトルを横に並べて
T = ( (

1
√2

1
√2
)
(

1
√2
− 1
√2
) ) = (

1
√2

1
√2

1
√2
− 1
√2
)
(3.46)
のようにして作る。
　なぜ規格化するかというと、一つの理由は規格化することによってTに対するT−1の計算が（「計 算」 とは呼べないほどに）簡単になるのである。今、N×N行列に対して固有ベクトルN本（→v1,→v2,…,→vN） を見つけたとしよう。このベクトルを並べて
T = ( (
 
 

→
v
 
1 
 
 
)
(
 
 

→
v
 
2 
 
 
) … (
 
 

→
v
 
N 
 
 
) )
(3.47)
を作る。さらにこの行列の行と列を入れ替える。つまり、

(
a
b
c
d
)      →　 　　 (
a
c
b
d
)

のような操作を行うと、
Tt= (

(        →
v
 
 t
1 
       )

(        →
v
 
 t
2 
       )
:

(        →
v
 
 t
N 
       )
)
(3.48)
となる。ただしここで、記号tは「転置(transpose)」（行と列を入れ替える操作）を表す。 (      →vit      )は列ベクトル
(
 
 

→
v
 
i

 
 
)
を横に並べ直したもの（これも転置）である。
　ここで、固有ベクトルに関するある定理を証明する。

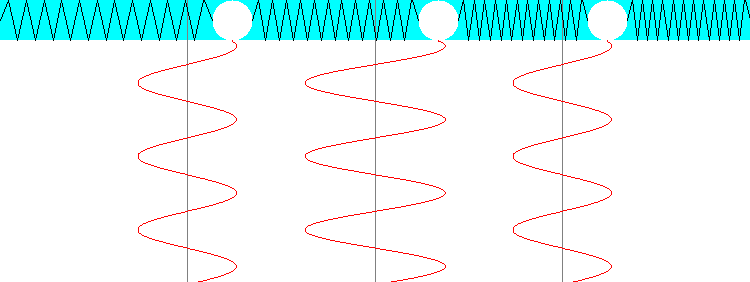
固有値の異なる固有ベクトルは直交する


 行列Mに対する固有値λ1の固有ベクトル→v1と 固有値λ2の固有ベクトル→v2を考える と、→v1·→v2=0 となる。なぜなら、 →v1t M→v2という量を考えると、
λ1 →
v
 
1 
 · →
v
 
2 
 ←


→
v
 
 t
1 
 M
=λ1→v1t 
→
v
 
2 
 ← →
v
 
 t
1 
 M →
v
 
2 
 → →
v
 
 t
1 


M →
v
 
2 
=λ2→v2 
 → λ2 →
v
 
1 
 · →
v
 
2 
(3.49)
という計算により、λ1(→v1·→v2)=λ2(→v1·→v2) となってしまうが、λ1 ≠ λ2なのだから、→v1·→v2=0でなくてはならない。

　よって固有ベクトルと固有ベクトルの内積を取ると、

→
v
 
i 
 · →
v
 
j 
 = {
0
i ≠ jの時
1
i= jの時

(3.50)
となる（すでに→viは規格化されていたとしている）。この式の意 味するところは、TtT=Iである。つまり、T−1はTtに 等しい39。
　ここで、N成分のベクトルに対して、互いに直交するN個の固有ベクトルを求めることができた。このN個のベクトルの適当な線形結合

→
V
 
 =a1 →
v
 
1 
 +a2 →
v
 
2 
 +a3 →
v
 
3 
 +·+aN →
v
 
N 
(3.51)
を取れば、任意のN成分ベクトルを作ることができるだろう。逆に、どんな初期条件を与えられても、その系の運動の状態を固有ベクトル（つまり振動のモー ド）の和で表すことができる（これを「モード分解」と呼ぶ）。
　以上のようにして、固有値と固有ベクトルを作れば、TとT−1も自動的にできあがり、問題は解ける こ とになる。

3.4  ３個の連結物体の振動

　では、具体的な例をもう一つ。今度は３個の物体（質量m）を４本のばね（ばね定数は全てk）で図のようにつなごう。
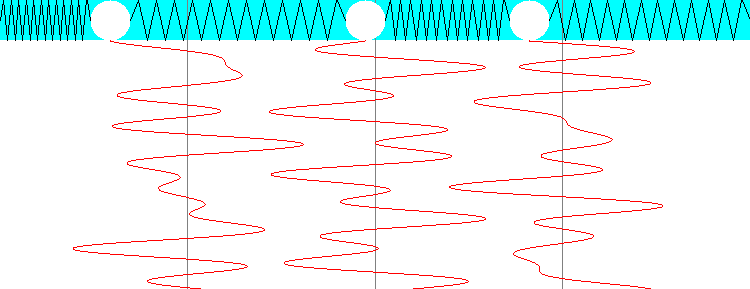
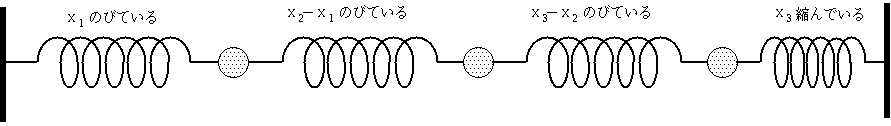　３つの場合の運動方程式は、行列で表現すると
m d2
dt2
(
x1
x2
x3
) = (
−2k
k
0
k
−2k
k
0
k
−2k
)
(
x1
x2
x3
)
(3.52)
である。

3.4.1  行列を使って解く

　まず固有値を求めるために


det
(
−2k−λ
k
0
k
−2k−λ
k
0
k
−2k−λ

) =
0
(−2k−λ)3−2k2(−2k−λ)=
0
(−2k−λ)( (−2k−λ)2−2k2) =
0
(−2k−λ)( (−(2+√2)k−λ) (−(2−√2)k−λ)) =
0

(3.53)
という方程式を解けば、λ = −2k,−(2+√2)k,−(2−√2)kという３つの固有値が出る。
　λ = −2kとなる場合、固有ベクトルは、

(
0
k
0
k
0
k
0
k
0

)
(
a
b
c
) =0   → {
bk=0
２行目から
ak+ck=0
１ 行目と３行目から

(3.54)
を満たす。こうなるためにはb=0,c=−aであればよいから、固有ベクトルは
(
1
0
-1
)
に比例する。長さが1になるようにすると、
(
1/√2
0
−1/√2
)
が固有ベクトルとなる。次にλ = −(2±√2)kの時は、

(
±√2k
k
0
k
±√2k
k
0
k
±√2k

)
(
a
b
c
) =0
(3.55)
を満たすベクトルを探せばよい。１行目からb=±√2aであることがわかり、３行目からb=±√2cであることがわかる。よって固有ベクトルは
(
±1/√2
1
±1/√2
)
に比例する。規格化すると
(
±1/2
1/√2
±1/2
)
である。これで３つの固有値、３つの固有ベクトルが求まった。行列で書くと、

(

1
2

1
√2

1
2

1
√2
0
− 1
√2
− 1
2

1
√2
− 1
2
)
(
−2k
k
0
k
−2k
k
0
k
−2k
)
(

1
2

1
√2
− 1
2

1
√2
0

1
√2

1
2
− 1
√2
− 1
2
) = (
−(2−√2)k
0
0
0
−2k
0
0
0
−(2+√2)k
)
(3.56)
という計算を行ったことになる。

以上のようにして変数変換を行った結果、運動方程式は
m d2
dt2
(
X1
X2
X3
) = (
−(2−√2)k X1
−2k X2
−(2+√2)k X3
)
(3.57)
であり、３つのモード(X1,X2,X3)は、おのおの√{[(2−√2) k/m]},√{[2k/m]},√{[((2+√2)k)/m]}の角振動数で振動する。

3.4.2  ３つのモードを図解する

　計算で求めた３つのモードがどんな運動なのかを考えてみよう。もっとも振動数の低いモードは固有ベクトル
(
1/2
1/√2
1/2
)
に対応する。つまり３つのおもりが全て同じ方向に振動する振動である。
　第２のモードは固有ベクトル
(
1/√2
0
−1/√2
)
に対応し、振動数は√{[2k/m]}である。これは左右対称な振動モードで、中央のおもりは動かない。
　最後の、もっとも振動数の高いモードは固有ベクトル
(
−1/2
1/√2
−1/2
)
に対応する。つまり真ん中のおもりは両側とは逆向きに動く。
　３つのおもりの運動x1,x2,x3は

(
x1
x2
x3
) = (

1
2

1
√2
− 1
2

1
√2
0

1
√2

1
2
− 1
√2
− 1
2
)
(
X1
X2
X3
)   すなわち    {
x1= 1
2
 X1+ 1
√2
 X2− 1
2
 X3

x2= 1
√2
 X1+ 1
√2
 X3

x3= 1
2
 X1− 1
√2
 X2− 1
2
 X3


(3.58)
のように３つのモードで表されている。各々のモードは

X1
=
A1 sin (   √
(2−√2)k
m
 
 t +α1 )

(3.59)

X2
=
A2 sin (   √
2k
m
 
 t +α2 )

(3.60)

X3
=
A3 sin (
   √
(2+√2)k
m
 
 t +α3 )

(3.61)
と単振動するので、これを代入することでx1,x2,x3が計算できることになる。 A1,A2,A3,α1,α2,α3は 運動方程式だけでは決まらないパラメータであり、初期状態から決定していくことになる。
　なお、実際に起こる振動は３つのモードが重なったものであり、たとえば図のような複雑なものになる。

　この３つの連成振動のア プレットと、２〜１０個までの連成振動のアプレットを見せて、今日のところは終了。

Footnotes:

38重解が出る場合 は、同じ固有値を持つ固有ベクトルが複数本あるということになる。こういう場合「縮退(degenation)がある」という言い方をする。以下で扱うの は縮退がない場合のみ。
39転置行列と逆行列 が等しい行列を「直交行列(orthogonal matrix)」と呼ぶ。なぜ「直交」かということは、上のTの作り方を 見れば納得できる。「互いに直交する列ベクトルを並べて作った」からである。

学生からの感想・コメント

　この振動は、ずっと待っていると元の状態に戻るんですか？
　各モードの振動数の比が有理数じゃないので、厳密には戻りません。だいた い同じような形には戻りますが。

　縮退があるときと無いときで、バネの連結にはどんな違いがあるのですか？
　同じ振動数のモードが二つある時が縮退のある時です。今日やったようなバ ネの振動だと、あまり起こらないのでしょう。
　たとえば輪っかになって周期境界条件が課されているような問題だと、右行 きの波と左行きの波が縮退します。

　１０個の物体の運動で、右だけ変位している状態から動かすとエネルギーが左に伝わっていきま すが、十分時間が経つとエネルギーは平均化されるのですか？
　平均化もしますが、また一カ所にエネルギーが固まったり、いろんな変化を 繰り返します。

　バネのモードを重ねた時物体と物体の波どうしはどれくらい（時間的に）ずれているんですか？
　それは場合によるのでなんとも。波の伝わる速度がどのように計算できるか はそのうちに話すことがあると思います。

　パワーポイントで振動の様子を見るのはわかりやすい。
　パワーポイントじゃなくてJavaアプレットなんですが(^_^;)。

　３つも重なった振動を考えるのはたいへんだから、それぞれのモードにわけるという理解でいい ですか？
　便利な考え方だと思いました。
　そういう考え方です。モードを使うことで、単振動の方程式に持って行く。

　固有ベクトル を行列に書くときに、
(

1
2

1
√2
− 1
2

1
√2
0

1
√2

1
2
− 1
√2
− 1
2
)
と書いても、
(

1
√2

1
2
− 1
2

０
1
√2

1
√2
− 1
√2

1
2
− 1
2
)

と書いてもいいんですか？
　何か答えが変わるような気がします。

　いいんです。この二つの違いは対角化した後の行列が、
(
−(2−√2)k
0
0
0
−2k
0
0
0
−(2＋√2)k

)

となるか、

(
−2k
0
0
0
−(2−√2)k
0
0
0
−(2＋√2)k

)
となるかの違いです。これは、
(
X1
X2
X3
)

のX1とX2の立場が入れ替わっただけです。どれをX1と呼ぶか、どれをX2と呼ぶかは人間の都合で、物理とは無関係なのです。

　規格化で計算が簡単になることが理解できました（多数）。
　直交行列を作るという考え方は、とても便利で応用範囲が広いので、このや り方をつかんでおいてください。

　数学ですね。。。。がんばります。
　数学は、物理を理解するための言語です。数学の言葉をしゃべってこそ、物 理が語れる。

　「固有値の異なる固有ベクトルは直交する」という定理はとても便利だとわかった。
　これも応用範囲の広い考え方です。つかんでおきましょう。


File translated from TEX by TTHgold, version 3.63.
On 27 Nov 2006, 12:08.