| k′= | { |
|
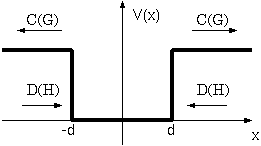 前節では遠方で減衰する解を計算した。その条件はV0 >
Eであった。この条件が満たされない時は、遠方でも減衰せずに波が進行していくことになる。このような場合の解を求めよう。やはり偶関数解を仮定すると、
前節では遠方で減衰する解を計算した。その条件はV0 >
Eであった。この条件が満たされない時は、遠方でも減衰せずに波が進行していくことになる。このような場合の解を求めよう。やはり偶関数解を仮定すると、
|
(14.13) |
|
(14.14) |
|
|
(14.17) |
|
(14.18) |
|
 2
k2)/2m]もE > V0で
あるという以外には、なんの制限もつかない。束縛状態で起こった、エネルギーの量子化は、ここでは起きない。数式上そのようになる理由は、束縛されている
場合には加えられていた「遠方で増大する解が落ちる」という条件が課されていないからである。よってエネルギーは連続的な値を取れる。これを「連続スペク
トルを持つ」とか「連続的固有値を持つ」とか言う。
なお、ここで求めた解は偶関数または奇関数であるため、必然的に左行きの波と右行きの波が同じ重みで(同じ振幅で)入っている。よって、「左から粒子が
入
射して、真中のポテンシャルで反射する波と、ポテンシャルを通り抜ける波に分かれる」という状況は、上の答えの中には入っていない。そのような状況にする
ためには、偶関数解と奇関数解を適当に組み合わせる必要がある。たとえば、(偶関数解)−D/H(奇関数
解)とすることで、
2
k2)/2m]もE > V0で
あるという以外には、なんの制限もつかない。束縛状態で起こった、エネルギーの量子化は、ここでは起きない。数式上そのようになる理由は、束縛されている
場合には加えられていた「遠方で増大する解が落ちる」という条件が課されていないからである。よってエネルギーは連続的な値を取れる。これを「連続スペク
トルを持つ」とか「連続的固有値を持つ」とか言う。
なお、ここで求めた解は偶関数または奇関数であるため、必然的に左行きの波と右行きの波が同じ重みで(同じ振幅で)入っている。よって、「左から粒子が
入
射して、真中のポテンシャルで反射する波と、ポテンシャルを通り抜ける波に分かれる」という状況は、上の答えの中には入っていない。そのような状況にする
ためには、偶関数解と奇関数解を適当に組み合わせる必要がある。たとえば、(偶関数解)−D/H(奇関数
解)とすることで、
|
(14.21) |
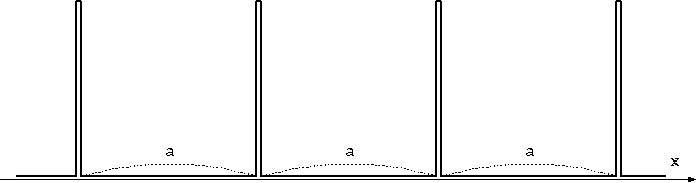
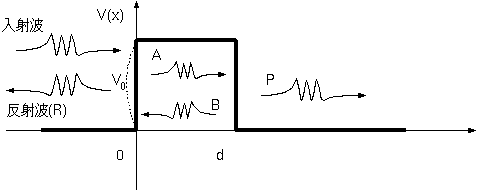 次に、図のように有限の長さと有限の高さを持つ壁を考えよう。0 < x < dの間だけV(x)=V0と
なり、通り
抜けた後は再びV(x)=0となるようなポテンシャルである71。
まず、壁の左側では入射波をeikx(これを振幅1として基準にする)、反射波をRe−ikxとおく。壁
の
内部ではAeik′x+Be−ik′xのように、左行きと右行きの波が共存している。壁を抜けて透過して行
く粒子の波動関数がPeik(x−d)(これは右行きのみ)で表せるとしよう。
次に、図のように有限の長さと有限の高さを持つ壁を考えよう。0 < x < dの間だけV(x)=V0と
なり、通り
抜けた後は再びV(x)=0となるようなポテンシャルである71。
まず、壁の左側では入射波をeikx(これを振幅1として基準にする)、反射波をRe−ikxとおく。壁
の
内部ではAeik′x+Be−ik′xのように、左行きと右行きの波が共存している。壁を抜けて透過して行
く粒子の波動関数がPeik(x−d)(これは右行きのみ)で表せるとしよう。
|
(14.22) |
|
(14.23) |
|
|
(14.28) |
|
|
|
(14.33) |
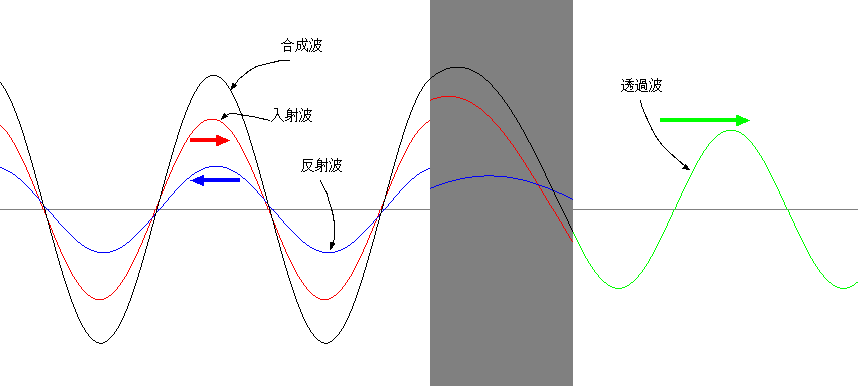
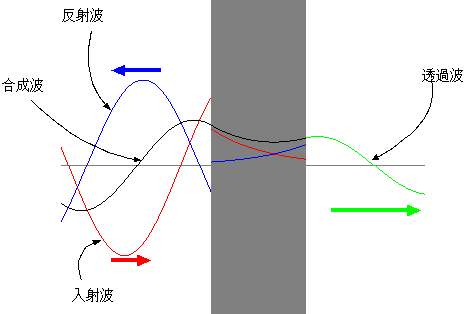 たとえV0 >
Eでも、Pは0にはならない。つまり、古典的には通過できないはずの壁がそこにあっても、粒子が向こう側へ通り抜ける確率は存在しているのである。ただ
し、その確率振幅にはe−κdの因子がかかっているから、d が大きい時やκが大きい(つまりEよりV0の
方がずっと大きい)時にはその確率は非常に0に近くなる。
なお、この場合、壁の中の波動関数は
たとえV0 >
Eでも、Pは0にはならない。つまり、古典的には通過できないはずの壁がそこにあっても、粒子が向こう側へ通り抜ける確率は存在しているのである。ただ
し、その確率振幅にはe−κdの因子がかかっているから、d が大きい時やκが大きい(つまりEよりV0の
方がずっと大きい)時にはその確率は非常に0に近くなる。
なお、この場合、壁の中の波動関数は
|
(14.34) |
|
|
(14.35) |
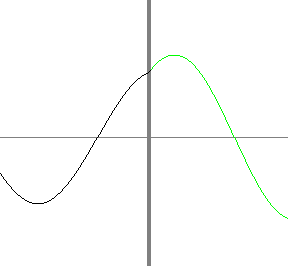 この式の右辺はもしV(x)に発散がないならd→0で0になり、微分[d/dx]ψは連続的につながる。しかしもしこの範囲でV(x)=V0δ(x)
のような発散があれば、
この式の右辺はもしV(x)に発散がないならd→0で0になり、微分[d/dx]ψは連続的につながる。しかしもしこの範囲でV(x)=V0δ(x)
のような発散があれば、
|
(14.36) |
|
(14.37) |
 2 k2)/2m]=E)。x
> 0とx < 0で係数A,Bが変化するだろう。これまで同様、入射波+反射波をeikx+Re−ikx、
透過波をPeikxとおけば、接続条件は
2 k2)/2m]=E)。x
> 0とx < 0で係数A,Bが変化するだろう。これまで同様、入射波+反射波をeikx+Re−ikx、
透過波をPeikxとおけば、接続条件は
|
|
(14.40) |
|
(14.41) |
|
(14.42) |
|
(14.43) |
|
(14.44) |
|
(14.45) |
|
(14.46) |
|
|
(14.49) |
|
(14.50) |
|
(14.51) |
|
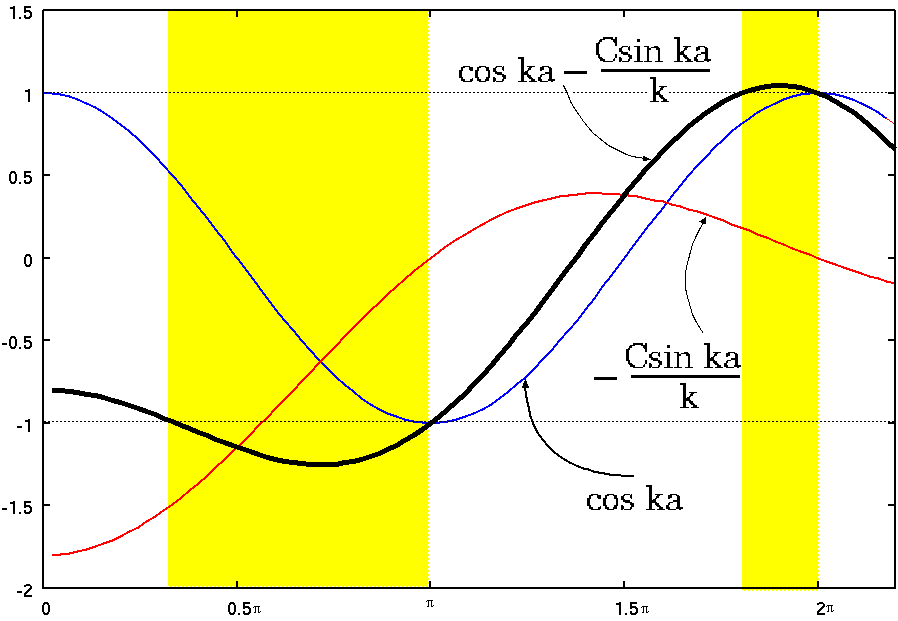
 2)]を−Cと書いていて、V0
< 0の場合である74。
ここではkが実数として考えたが、もちろんkが虚数になる事もありえて、その場合、k=iκとすると、
2)]を−Cと書いていて、V0
< 0の場合である74。
ここではkが実数として考えたが、もちろんkが虚数になる事もありえて、その場合、k=iκとすると、
|
(14.52) |
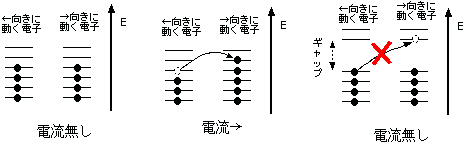
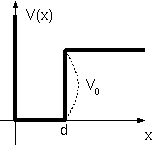 右のグラフで表されるポテンシャル
右のグラフで表されるポテンシャル
|
(14.53) |