量子力学講義録2005年第３回
第11章 分散と不確定性関係
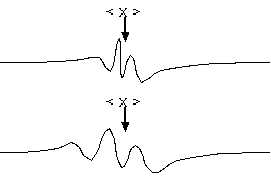左の図のように、おなじ < x > を持っていても、拡がりかたが全然違う波動関数もある。このような波動関数の拡がりの目安となる数字を計算する方法が欲しい。
これは量子力学に限ったことではない。たとえば、
97,95,101,103,99,105,103,98,101,98
という数列も、
82,98,125,76,131,110,87,82,103,106
という数列も、平均値を取るとどっちも100になるが、後者の方が「ばらつきが大きいなぁ」と感じるであろう。そのようなばらつきの違いを数字で表しておきたいのである。
そこでまず、ある値xと平均値 < x > とのずれ(x− < x > )を考える。しかし、単純にこれの平均を取ると0になってしまう。
平均値からのずれはプラスとマイナスが均等に表れるので足し算するとゼロになるのは当然であるし、
|
< x− < x > > = < x > − < x > =0 |
| (11.1) |
という計算をしてみても、これがゼロになるのは自明である。そこでずれを自乗して(プラスになるようにして)から平均をとる。つまり、下の表のような計算をする。
この、(ずれ)2の平均の大きさでばらつきの度合いを表す。これが「分散（distribution）」で、式で書くならば、 < (x− < x > )2 > となる。つまり、「xと、その期待値 < x > の差を自乗して、それの期待値をとったもの」である。
結果を表にすると、
|
|
|
|
|
|
|
|
|
|
| 平均値 |
| 値 | 97 | 95 | 101 | 103 | 99 | 105 | 103 | 98 | 101 | 98 | 100
|
| ずれ | -3 | -5 | +1 | +3 | -1 | +5 | +3 | -2 | +1 | -2 | 0
|
| (ずれ)2 | 9 | 25 | 1 | 9 | 1 | 25 | 9 | 4 | 1 | 4 | 8.8
|
のようになる。分散は8.8ということになる。
「ばらつき具合の目安にする」という条件だけならば絶対値|x− < x > |の平均でもよいし、自乗でなく４乗にしてもよさそうである。しかし計算する時は自乗平均が一番楽であるし、昔から使われているので、この計算をする。分散を計算するには、
|
< (x− < x > )2 > = < x2 −2x < x > + < x > 2 > = < x2 > −2 < x > < x > + < x > 2 = < x2 > − < x > 2 |
| (11.2) |
という計算をした方が簡単にできることもある。
なお、分散の平方根を標準偏差(standard deviation)と言う（さっきの例の場合、√[8.8] ≅ 2.966）。標準偏差はxと同じ次元になり、xの拡がり具合と直接結び付いた量となる50。量子力学の世界では分散を(∆x)2 と書いて、標準偏差にあたる∆xをxの不確定性(uncertainty)を表す数字として使う51。実験などの結果を整理するときに値の広がり具合を示すときにも標準偏差がよく使われる。
以上からわかるように、期待値( < x > )や分散( < (x− < x > )2 > または < x2 > − < x > 2)
あるいはその平方根である∆xは、波動関数が含んでいる情報のうち、ほんの一部分にすぎない。古典力学においては、位置xと運動量pがわかり、運動方程式
を知っていればその系について全てを予言することができた。しかし量子力学では < x > や < p >
がわかっただけでは、全体がわかったとは言えない。しかも観測できるのは期待値だけであって、波動関数ψそのものは我々には見えない。つまり、我々が「見
ている」世界というのはその裏に隠れている波動関数というものの、ほんの一部に過ぎないのである。「物理量に対応する演算子をもってきて、その期待値を取
る」という計算は、波動関数という非常にたくさんの情報を含むものの中の一部分の情報を引き出す計算であるということを心にとどめておくべきである。
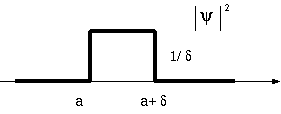
さて、ここで、
|
ψ(x)= | {
|
| 
|
| (11.3) |
のような単純な矩形波の場合で分散や標準偏差を計算しておくと、
| ∫
|
dx ψ* x2 ψ = |
1
δ
|
| [
|
x3
3
| ]
|
a+δ
a
|
= |
1
3δ
|
((a+δ)3 − a3) = |
1
3δ
|
(3a2 δ+ 3aδ2 + δ3) = a2 + aδ+ |
δ2
3
|
|
| (11.4) |
となり、分散はこれから( < x > )2=(a+[δ/2])2を引くので、
|
∆x2 = a2 + aδ+ |
δ2
3
|
− | ( |
a+ |
δ
2
| )
|
2
|
= |
δ2
3
|
− |
δ2
4
|
= |
δ2
12
|
|
| (11.5) |
となる。∆x=[δ/2√3]ということで、波の幅に比例した答えが出てくる(あくまで目安なので、ぴったりδにならないからと目くじらをたてることはない)。
|
[問い11-1]
確率密度ψ*ψが以下のようなグラフで表される波動関数がある。それぞれについて、hの値を規格化条件に合うように決めたのち、期待値と分散を計算せよ。
計算の前に各々の分散の大小関係を予測し、結果と比較すること。
(Hint:馬鹿正直に計算しようとすると、ちょっとたいへんかもしれない。こういう時は、計
算に都合がいいような座標系を自分で設定してから計算するのが楽である。たとえば、上の(2)であれば、x=aが原点になるような座標系x′=x−aを
使って計算するとだいぶ計算は楽である。)
|
|
11.2 不確定性関係と交換関係
位置の不確定度∆xと運動量の不確定度∆pの間には、∆x∆p ≥ [
/2]という関係52があった。これを期待値および分散という考えかたから導こう。まず、不確定度を標準偏差（分散の平方根）であるとして、
| |
|
|
< (p− < p > )2 > = | ∫
|
ψ* (p− < p > )2 ψdx |
|
| (11.6) |
| |
|
| < (x− < x > )2 > = | ∫
|
ψ* (x− < x > )2 ψdx |
|
| (11.7) |
|
としよう。これの積が一定値よりも大きいことを証明する。このふたつの量は、
|
ψ1=(p− < p > )ψ, ψ2=(x− < x > )ψ |
| (11.8) |
のような形の波動関数を考えると、
|
(∆p)2 = | ∫
|
ψ*1 ψ1 dx=(ψ1,ψ1), (∆x)2 = | ∫
|
ψ*2 ψ2 dx=(ψ2,ψ2) |
| (11.9) |
と書ける。ただし(ψ,φ)=∫ψ* φdxという、ベクトルの内積の真似をした記法を使って書いている(波動関数はベクトル的に扱うことができる)。記号(ψ,φ)は「ψの複素共役とφをかけてから積分する」という意味であるので、(ψ,φ)=(φ,ψ)*という性質を持つ。特に(φ,φ) ≥ 0である(もちろん(φ,φ)は実数。等号が成立するのはφがいたるところで0である場合のみ)53。
波動関数ψに対し、√{(φ,φ)}のことを波動関数のノルム(norm)と呼ぶ。ノルムはベクトルの長さに対応し、規格化されているならば1である。
物理においてよく使われる空間ベクトルに関する公式として
|
( |
→
a
|
· |
→
a
|
)( |
→
b
|
· |
→
b
|
) ≥ ( |
→
a
|
· |
→
b
|
)2 |
| (11.10) |
というものがある。この式は内積の定義→a·→b=|→a||→b|cosθからも導けるし、二つのベクトルを任意に実数αをかけて引いたベクトル→a−α→bの長さが、αの値にかかわらず常に0以上であること(式で書けば(→a−α→b)2 ≥ 0)からも証明できる。すぐ後でこれの波動関数バージョンの証明をする。
|
[問い11-2]
(11.10)を、任意のベクトル→a,→bと任意の実数αについて、(→a−α→b)2 ≥ 0が成立することを使って証明せよ。
|
|
この式の左辺が二つのベクトルの長さの自乗の形になっていることに注意せよ。今求めたい∆p∆xも自乗すれば、(∆p)2(∆x)2=(ψ1,ψ1)(ψ2,ψ2) となって、(11.10)の左辺に似た形となる。この式の波動関数バージョンの式を使うと、∆x ∆pの最小値への手がかりが得られそうである。
そこでまず、以下で(11.10)の波動関数バージョンとなる一般的な式を証明しよう。まずはψ1,ψ2を一般の波動関数として、ψ1−αψ2という波動関数を作る。α は複素数としよう。自分自身との内積(ノルムの自乗)は0以上になるということから、
|
| |
|
(ψ1,ψ1)−α(ψ1,ψ2)−α* (ψ2,ψ1)+αα* (ψ2,ψ2) |
| |
|
|
| (11.11) |
になる。ここで、内積の定義から(ψ1,αψ2)=α(ψ1,ψ2)および(αψ2,ψ1)=α*(ψ2,ψ1)が言えることに注意。すなわち、定数が内積の中から外に出る時は、後ろから出るならそのままだが、前から出るなら複素共役になって出てくる(定義(ψ,φ)=∫ψ*φdx をよく見よ)。
ここでα = kとしてkが実数であるとすれば、
|
|
(ψ1,ψ1)−k( (ψ1,ψ2)+ (ψ2,ψ1))+k2 (ψ2,ψ2) |
| |
|
|
| (11.12) |
となるし、α = ikのようにαが純虚数だとすれば、
|
|
(ψ1,ψ1)−ik( (ψ1,ψ2)−(ψ2,ψ1))+k2 (ψ2,ψ2) |
| |
|
|
| (11.13) |
という式が出る。
どちらの式も、ak2 + bk+c ≥ 0というkに関する二次不等式の形に書けた。双方とも、a=(ψ2,ψ2),c=(ψ1,ψ1)であり、bは上の式では、− ( (ψ1,ψ2) + (ψ2,ψ1) )、下の式では−i( (ψ1,ψ2) −(ψ2,ψ1) )である。係数a,b,cは全て実数であることに注意せよ。だから実数係数の二次不等式での公式がすべて使える。
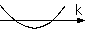これらの式はkの値によらず成立しなくてはいけないが、もし(左辺)=0
という方程式が二つの実数解を持つと、右のようなグラフが書けることになってしまって負になってしまう。それゆえこの式は実数解をせいぜい一つしかもたな
い。その条件は判別式が0以下であるということ、すなわちb2−4ac ≤ 0である。ゆえに
|
[−((ψ1,ψ2)+(ψ2,ψ1))]2−4(ψ1,ψ1)(ψ2,ψ2) ≤ 0 |
| (11.14) |
または
|
[−i((ψ1,ψ2)−(ψ2,ψ1))]2−4(ψ1,ψ1)(ψ2,ψ2) ≤ 0 |
| (11.15) |
という式が出る。一見二つの式のようだが、実は(11.14)で
ψ2→ iψ2と置き換えを行えば(11.15)が出てくる。以下で
は(11.15)だけ計算する。
ここまでは一般式だったが、ここで(11.15)の中のψ1,ψ2に(11.8)で定義された波動関数を代入する。
第二項は−4(∆x)2(∆p)2となる。第一項を計算しよう。
|
|
| [
|
−i | ∫
|
ψ*(p− < p > )(x− < x > )ψdx− | ∫
|
ψ*(x− < x > )(p− < p > )ψdx | ]
|
2
|
|
|
|
| [
|
−i | ∫
|
ψ* |
[p− < p > ,x− < x > ]
=−i |
ψdx | ]
|
2
|
|
|
|
| [
|
− | ∫
|
ψ* ψdx | ]
|
2
|
= 2 |
|
|
|
| (11.16) |
となる。ここで [ p− < p > ,x− < x > ] を計算する時には、 < x > , < p > はもはや数であって演算子ではないので、xやpと交換することを用いた。
交換関係のところ、なぜ＜ｘ＞とかを消せるんですか？
＜ｘ＞はもう期待値を計算し終わったあとのものなので、ただの数なんです。ただの数だとｐ＜ｘ＞＝＜ｘ＞ｐなので、交換関係の中にいれてもないのと同じです。交換関係の中に「ただの数」が入った時にはいつもこうできます。
よって、
| 2 − 4 (∆x)2 (∆p)2 ≤ 0 |
| (11.17) |
である。これからただちに、
|
(∆x)2 (∆p)2 ≥ | 2
4
|
すなわち ∆x ∆p ≥ |
2
|
|
| (11.18) |
が導かれる。これが不確定性関係である。
前に不確定性関係が出た時は「＞ｈ」だったと思うんですが、いいんですか？
前にやったのはおおざっぱな計算だったので、おおまかな値が出てたんだと思ってください。ここでやったのは厳密な計算です。でもほとんどの場合、不確定性は、/2よりも大きくなるので、「＞ｈ」でもほとんどの場合間違いじゃありません。実際の波動関数の場合のΔｘやΔｐは、もっとぼやけてます。
|
[問い11-3]
導出方法からわかるように、∆x∆pが最小値である[/2]になる時は、ψ1=(p− < p > )ψ,ψ2=(x− < x > )ψのような形の波動関数の間にψ1 − ikψ2=0(kはある実数)が成立する時である(この時にのみ(ψ1−ikψ2,ψ1−ikψ2)=
0になる)。簡単のために < x > = < p >
=0の場合についてこの式を解いて、∆x∆pが最小になる時の波動関数がどんな形になるか、求めよ。この波動関数は、「不確定性が最小になっている」とい
うことで、最小波束(minimum packet)と呼ばれる。
|
|
Footnotes:
50受験で悪名高い偏
差値というのは、平均(期待値)を偏差値50と定め、平均点から標準偏差分だけ外れたら偏差値が10違う、というふうに決めた数字。平均点が72点で標準
偏差が15という分布があったとすると、87点取った人が偏差値60、57点取った人は偏差値40ということになる。平均点が同じだったとしても、標準偏
差が小さい分布の時の方が「平均より10点だけ高得点を取る」ことの価値は大きい。それを示すのが偏差値の役割。
51不確定性関係の話をする時、特に厳密な定義を与えずに∆x,∆pを用いたが、厳密には分散で定義するべきであった。
52たいていの場合、∆x∆p > hと書いてあるが、正確にはこう。
53「場の量子論」と呼ばれる量子力学の無限自由度系バージョンにおいては、自分自身との内積が負になるような場合を考えなくてはいけない場合もある。量子力学では(φ,φ) ≥ 0と考えてよい。
学生の質問・コメントから
ずれを自乗して平均取って分散を出しますが、なぜずれの絶対値でしないのですか？
いろいろ理由はあると思いますが、絶対値を取るということは「＋かーか」で場合分けすることになって、かえって計算が面倒になるということもあるし、自乗用にいろいろ便利な公式があることもあるでしょう。
判別式D=b2-4acが出てきたのが懐かしかった。（多数）
高校の数学も役に立つもんでしょ。
∫φ*ψdxが内積だというのがしっくりこない。
12章で、波動関数がベクトルだというのはどういう意味なのかをやりますので、少し待ってください。
最後に言っていた「不確定性関係が崩れる」というのはどういう意味ですか？
「不確定性関係がくずれる」という意味ではなくて「ΔｘΔｐは／２よりも遙かに大きいことが多いので、ΔｘΔｐ≥／２という式はあるけど、実際にはそれよりももっとぼやけた関係式ΔｘΔｐ＞ｈになっていることが多い」ということです。
不確定性関係が不確定性原理と呼ばれていたのは、最初に言い出した人が証明できなかったからでしょうか？
最初に言い出したのはハイゼンベルクですが、その時代はそもそも量子力学が完成していなかったのです。だからある意味、その時代は何が証明できて何が証
明できていないんだが、よくわからない混沌の時代だった。だから何を「原理」と考えるべきかもよくわからなかったのでしょう。
テキストの後ろにある演習問題は授業中にやるんですか？
基本的にはやりません。「問い」は宿題として出します。演習問題は、元気のある人が力試しにやってみてください。
（φ,ψ）という記号は便利ですね。
他にも＜φ｜ψ＞なんて記号もあります。
（φ,ψ）はディラックのブラケット＜φ｜ψ＞と同じものですか？
同じものです。ブラケットの方が、間に演算子をはさむ時の書き方がわかりやすいですね。ブラケットは便利ではありますが、この授業では使わないで説明していく予定です。
File translated from
TEX
by
TTHgold,
version 3.63.
On 27 Oct 2005, 13:10.