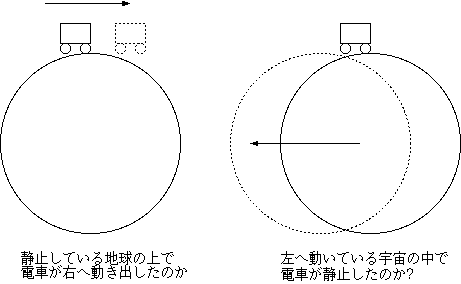
世の中に「自分は絶対静止している」と主張できるものなどないというのが相対論の主張である。
 ここで、「宇宙で静止しているものは何かが判定できるか」という問題を考えてみよう。
話を簡単にするため、宇宙には地球とその表面の物体しかなく、地球は自転も公転もしていないとしよう。この孤独な地球の上にあなたが住んでいて、今電車
に乗っているとする。電車が加速も減速もせず曲がりもせずにスムースに走っている時、電車の中であなたがする行動(本を読んだりあくびしたり、あるいはす
いていればキャッチボールだって)は、家の中での行動と同じように、何の支障もなくできるはずだ2。この現象を「宇宙が止まっていて、電車が等速運動している」と考えることもで
きるし、「電車が止まっていて、宇宙全体が逆向きに等速運動している」と考えることもできる。どちらで考えても、電車内で起こる物理現象は同じである。つ
まり、どっちが静止しているのか、判断する方法はないのである。
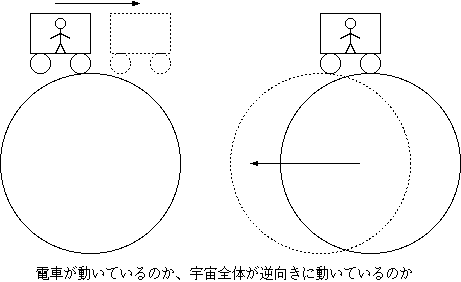
ここで、「宇宙で静止しているものは何かが判定できるか」という問題を考えてみよう。
話を簡単にするため、宇宙には地球とその表面の物体しかなく、地球は自転も公転もしていないとしよう。この孤独な地球の上にあなたが住んでいて、今電車
に乗っているとする。電車が加速も減速もせず曲がりもせずにスムースに走っている時、電車の中であなたがする行動(本を読んだりあくびしたり、あるいはす
いていればキャッチボールだって)は、家の中での行動と同じように、何の支障もなくできるはずだ2。この現象を「宇宙が止まっていて、電車が等速運動している」と考えることもで
きるし、「電車が止まっていて、宇宙全体が逆向きに等速運動している」と考えることもできる。どちらで考えても、電車内で起こる物理現象は同じである。つ
まり、どっちが静止しているのか、判断する方法はないのである。
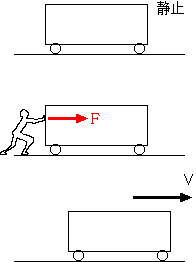 左図の図のような運動(電車を人間が押した
ら動き出した)を地球静止説に立って解釈すれば、
左図の図のような運動(電車を人間が押した
ら動き出した)を地球静止説に立って解釈すれば、
|
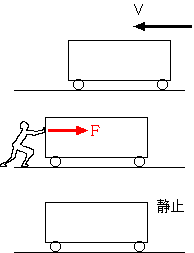 この場合の解釈は、
この場合の解釈は、
|
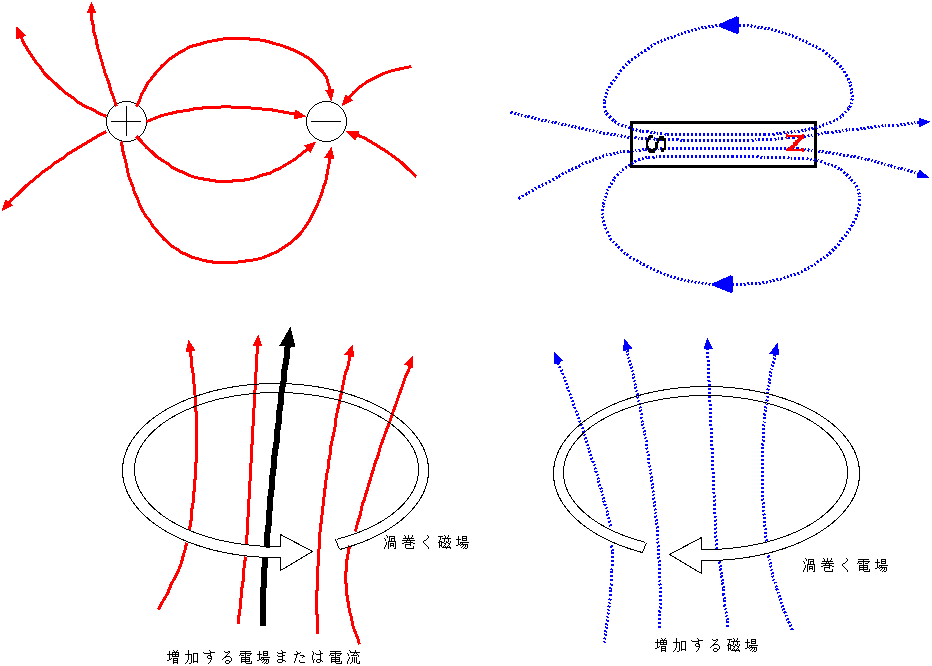
| div→D = ρ |
| div→B = 0 |
| rot→E = −[∂/∂t]→B |
| rot→H = →j + [∂/∂t]→D |
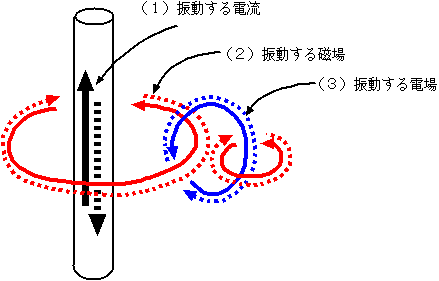 (1)ある場所に振動する電流または電束密度が発生する(たとえば電波のアンテナなら周期的に変動する電流を流している)。
(2)「電流」もしくは「電束密度の時間変化」は、周囲に渦をまくような磁場を伴う(rot→H=→j+[∂/∂t]→D)。
(3)周囲の空間の磁場が時間変動には、さらにその周囲に渦をまくような電場を伴う(rot→E=
−[∂/∂t]→B)。
以上がくりかえされることにより、空間の中を電場と磁場の振動が広がっていく。
(1)ある場所に振動する電流または電束密度が発生する(たとえば電波のアンテナなら周期的に変動する電流を流している)。
(2)「電流」もしくは「電束密度の時間変化」は、周囲に渦をまくような磁場を伴う(rot→H=→j+[∂/∂t]→D)。
(3)周囲の空間の磁場が時間変動には、さらにその周囲に渦をまくような電場を伴う(rot→E=
−[∂/∂t]→B)。
以上がくりかえされることにより、空間の中を電場と磁場の振動が広がっていく。
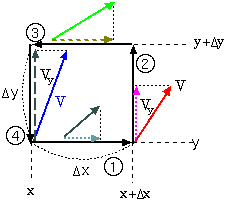 なお、図ではrotがゼロでない状態の電場を、まるで渦を巻いているかのように書いたが、rotがゼロでないからと言って別
に渦を巻く必要はない。もともとrotの定義は左の図のように、微小な四角形の辺の上を一周した時、ベクトル場が働く力だとしたらどれぐらい仕事をしても
らえるかを足し算したもの(最後に四角形の面積∆x∆yで割る)である。左の図の場合、
x方向に∆x動くから仕事はVx(x,y)∆x。
y方向に∆y動くから仕事はVy(x+∆x,y)∆y。
x方向に−∆x動くから仕事は−Vx(x,y+∆y)∆x。
y方向に−∆y動くから仕事は−Vy(x,y)∆x。
となって、この4つの和は
なお、図ではrotがゼロでない状態の電場を、まるで渦を巻いているかのように書いたが、rotがゼロでないからと言って別
に渦を巻く必要はない。もともとrotの定義は左の図のように、微小な四角形の辺の上を一周した時、ベクトル場が働く力だとしたらどれぐらい仕事をしても
らえるかを足し算したもの(最後に四角形の面積∆x∆yで割る)である。左の図の場合、
x方向に∆x動くから仕事はVx(x,y)∆x。
y方向に∆y動くから仕事はVy(x+∆x,y)∆y。
x方向に−∆x動くから仕事は−Vx(x,y+∆y)∆x。
y方向に−∆y動くから仕事は−Vy(x,y)∆x。
となって、この4つの和は
|
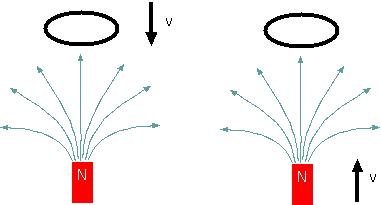 電磁波(光)の速度以外にもう一つ、アインシュタインが疑問としたのは電磁誘導という現象をどのように解釈するかである。アインシュタインの考察した現
象とは少し違うが、以下のような現象を考えよう。磁石にコイルを近づける(左図)、あるいはコイルに磁石を近づける(右図)、このどちらを行ってもコイル
には電流が流れる。この二つの現象は、「相対的に」考えるならば、全く同じものである。というのは、左図の状態を、コイルと同じ速さで同じ方向に動いてい
る人がみれば、まさに右図の状態が見えるはずだからである。しかし電流の発生する原因の解釈は同じではない。
右図の場合、コイルに電流が流れる理由は、「磁束密度の変化によって渦を巻くような誘導電場が発生したから」(rot→E = −[(∂→B)/∂t])
である。一方、左図の場合、電流が流れる理由は「磁場中を電子が下向きに動いたので、ローレンツ力によって電子が動かされたから」である。
この時、ある場所の磁束密度→Bは変化しないから、[(∂→B)/∂t]=0である。つまり電場の発生はない8。
くわしい計算は後でもう一度実行するが、どちらの立場で計算しても流れる電流は同じになる。このように、同じ現象のように見えるのに、違う筋道の説明が
2種類ある。そしてどちらも、マックスウェル方程式を使った計算で正しい答が出る。となれば、「どんな立場でもマックスウェル方程式は成立する」と考えた
いところである。
電磁波(光)の速度以外にもう一つ、アインシュタインが疑問としたのは電磁誘導という現象をどのように解釈するかである。アインシュタインの考察した現
象とは少し違うが、以下のような現象を考えよう。磁石にコイルを近づける(左図)、あるいはコイルに磁石を近づける(右図)、このどちらを行ってもコイル
には電流が流れる。この二つの現象は、「相対的に」考えるならば、全く同じものである。というのは、左図の状態を、コイルと同じ速さで同じ方向に動いてい
る人がみれば、まさに右図の状態が見えるはずだからである。しかし電流の発生する原因の解釈は同じではない。
右図の場合、コイルに電流が流れる理由は、「磁束密度の変化によって渦を巻くような誘導電場が発生したから」(rot→E = −[(∂→B)/∂t])
である。一方、左図の場合、電流が流れる理由は「磁場中を電子が下向きに動いたので、ローレンツ力によって電子が動かされたから」である。
この時、ある場所の磁束密度→Bは変化しないから、[(∂→B)/∂t]=0である。つまり電場の発生はない8。
くわしい計算は後でもう一度実行するが、どちらの立場で計算しても流れる電流は同じになる。このように、同じ現象のように見えるのに、違う筋道の説明が
2種類ある。そしてどちらも、マックスウェル方程式を使った計算で正しい答が出る。となれば、「どんな立場でもマックスウェル方程式は成立する」と考えた
いところである。