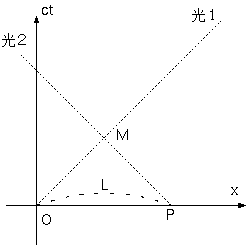
 右の図は、ある座標系(ct,x)を使って、二つの逆向きに進む光の進路を点線で
表したものである。光1は点O(0,0)を出発して右へ進み、光2は点P(0,L)を出発し
て左に進む。すれ違いの起こる場所をM点とする。
上の文章で、(ct,x)のところが逆に(x,
ct)となってました。
x=0とx=Lに、それぞれ観測者αとβが静止している。
(1)
解答用紙にこのグラフを書いて、
右の図は、ある座標系(ct,x)を使って、二つの逆向きに進む光の進路を点線で
表したものである。光1は点O(0,0)を出発して右へ進み、光2は点P(0,L)を出発し
て左に進む。すれ違いの起こる場所をM点とする。
上の文章で、(ct,x)のところが逆に(x,
ct)となってました。
x=0とx=Lに、それぞれ観測者αとβが静止している。
(1)
解答用紙にこのグラフを書いて、

|
|
|
|
|
|
|
|
|
|
|
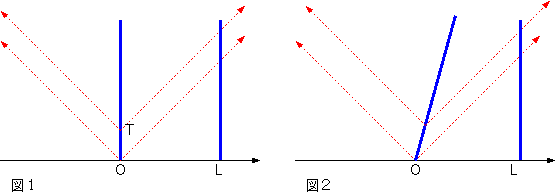 図1は、x=0に静止した光源が、時間T経過するごとにパルス波を出している様子を描いた時空図である。x=Lには観測者がおり、光源からくる光を観測し
ている。この場合、最初のパルス波が出るのは(ct,x)が(0,0)であり、第2のパルス波が出るのは(cT,0)となる。
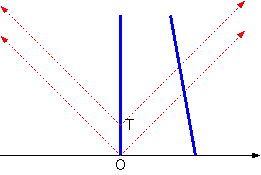
図2は観測者が動かず、光源が速さvで右(x軸正の向き)に動いた場合の時
空図である。1回目のパルス波は(0,0)で出る。2回目のパルス波は、光源の固有時がT進んだ時に出る。
図1は、x=0に静止した光源が、時間T経過するごとにパルス波を出している様子を描いた時空図である。x=Lには観測者がおり、光源からくる光を観測し
ている。この場合、最初のパルス波が出るのは(ct,x)が(0,0)であり、第2のパルス波が出るのは(cT,0)となる。
図2は観測者が動かず、光源が速さvで右(x軸正の向き)に動いた場合の時
空図である。1回目のパルス波は(0,0)で出る。2回目のパルス波は、光源の固有時がT進んだ時に出る。
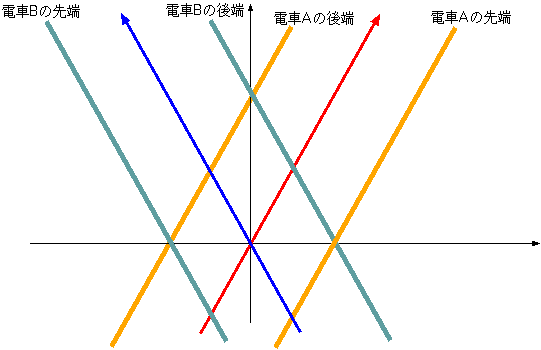
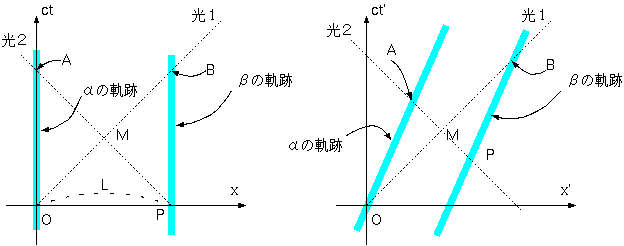
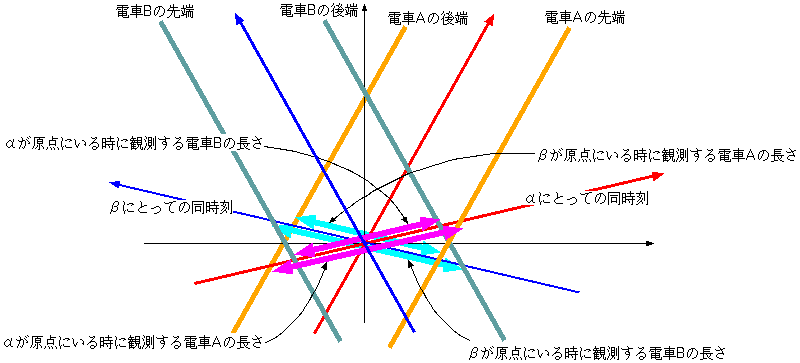 αは自分の同時刻(図の「αにとっての同時刻」)の線上で長さを測る。図に示した長さを見ると、「αから見た電車Bの長さ」は「αから見た電車Aの長
さ」の内側にあり、確かに短い。逆も同様。
αは自分の同時刻(図の「αにとっての同時刻」)の線上で長さを測る。図に示した長さを見ると、「αから見た電車Bの長さ」は「αから見た電車Aの長
さ」の内側にあり、確かに短い。逆も同様。
|
|
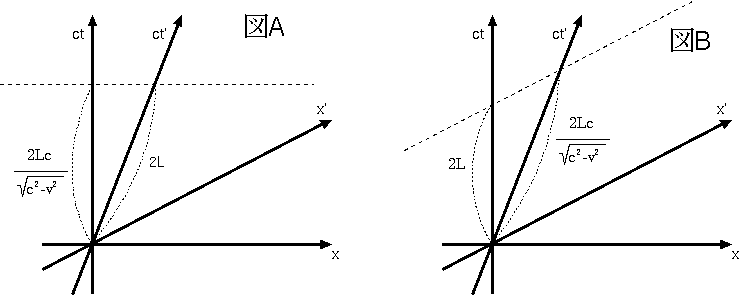 図Aの点線は、(ct,x)座標系での同時刻、図Bの点線は、(ct′,x′)座標系での
同時刻である。図Aの立場の同時刻において、ct軸上を動いてきた物体 の経験した時刻とct′軸上を動いてきた物体の経験した時刻を比べると、
後者の方が短い(動いている物体の方が時間が遅れる)。
一方、図Bの立場では、同時刻が違っているため、比較している場所が違う。こ うして、「同時刻」の違いによって「互いの時計が遅れる」という現象
が起こってもおかしくない。
図Aの点線は、(ct,x)座標系での同時刻、図Bの点線は、(ct′,x′)座標系での
同時刻である。図Aの立場の同時刻において、ct軸上を動いてきた物体 の経験した時刻とct′軸上を動いてきた物体の経験した時刻を比べると、
後者の方が短い(動いている物体の方が時間が遅れる)。
一方、図Bの立場では、同時刻が違っているため、比較している場所が違う。こ うして、「同時刻」の違いによって「互いの時計が遅れる」という現象
が起こってもおかしくない。
|
|
|
|
|