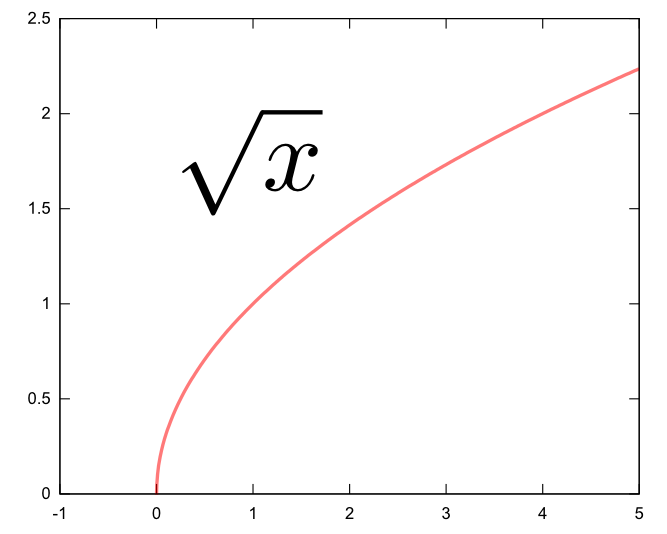
テイラー展開が可能であるためには、$f(x_0)$はもちろん、任意の階数の微係数${\mathrm d \over \mathrm dx}f(x_0),{\mathrm d ^2\over \mathrm dx^2}f(x_0),\cdots$が全て計算できる場所でなくてはいけない。たとえば、$f({x})=\sqrt{{x}}$を原点${x}=0$の回りにテイラー展開することはできない(つまり、この関数は原点において解析的でない)。${\mathrm d \over \mathrm dx}f({x})={1\over 2\sqrt{{x}}}$なので、${x}=0$では微分が存在しない(あえて書くなら$\infty$)。グラフでは、${x}=0$において線が垂直に立っていることで「微分できない」ことが表現されている。
では$\sqrt{{x}}$のような関数はどうやって近似するかというと、${x}=0$以外、たとえば${x}=1$の回りにテイラー展開する。${x}=1$でなら、${1\over 2\sqrt{{x}}}\biggr|_{{x}=1}={1\over 2}$となってちゃんと値がある。二階微分も計算しておくと、${\mathrm d ^2\over \mathrm dx^2}\sqrt{{x}}=-{1\over 4{x}^{3\over 2}}$となるから2次の項の係数は${1\over 2}{\mathrm d ^2\over \mathrm dx^2}\sqrt{{x}}\bigr|_{{x}=x_0}=-{1\over 8}$であり(3次以上の項については詳細は省くが同様の計算を行って)、
\begin{equation} \sqrt{{x}}= 1 +{1\over 2}({x}-1)-{1\over 8}({x}-1)^2+{1\over 16}({x}-1)^3-{5\over 128}({x}-1)^4+\cdots \end{equation}のように展開できる。たとえば電卓を叩けば$\sqrt{1.2}\fallingdotseq1.09544511501033\cdots$という式が出るが、電卓内部では上のような展開を使って計算される。ちょっとやってみると、
\begin{equation} \sqrt{1.2}= \underbrace{\underbrace{\underbrace{\underbrace{1 +\underbrace{{1\over 2}(1.2-1)}_{0.1}}_{1.1}-\underbrace{{1\over 8}(1.2-1)^2}_{0.005}}_{1.095}+\underbrace{{1\over 16}(1.2-1)^3}_{0.0005}}_{1.0955}-\underbrace{{5\over 128}(1.2-1)^4}_{0.0000625}}_{1.0954375}+\cdots \end{equation}のようにして正しい値に近づいていく。
←cosのテイラー展開へ ↑第11講の最初へ logのテイラー展開へ→