合成関数
関数は「数→数」の対応関係であるが、この対応関係を二段階にしたもの「数→数→数」を「合成関数」と呼ぶ。
たとえば、ある気体を電気ヒーターで暖めているとしよう。ヒーターの電力を変えれば温度が変わる(電力→温度)。そして、温度が変わればその気体中の音速が変わる(温度→音速)。こうすると「電力を変えれば(温度の変化を通じて)音速が変わる」(電力→温度→音速)という関数関係ができることになる。
新米なら650円の時給が、熟練すると800円に上ったりする。これは1つの関数。一ヶ月に働く時間が決まっているとすれば、時給が決まれば月給が決まる。これが二つめの関数。この二つの関数を合成すると「熟練度」→「月給」という関数ができる。
こんなふうに日常的な話でも「関連する数の変化を追いかけて合成していく」ということをやっている。これが「合成関数」の気持ち。
数式の例をあげよう。${y}=1-{x^2}$という${x}\to {y}$という対応関係があり、さらに${z}=\sqrt{{y}}$という${y}\to {z}$の対応関係があれば、この二つをまとめて、${z}=\sqrt{1-{x}^2}$という${x}\to{z}$という「合成関数」を作ることができる。
二つの関数を${y}=f({x})$(yがxの関数である)および${z}=g({y})$(zがyの関数である)と書けば、合成関数は${z}=g(f({x}))$のように書ける(この式の意味は「まず$f({x})$を計算して、計算結果を$g({y})$のyに代入すると、zが求められる」ということだ)$g(f({x}))$を$(g\circ f)({x})$と書くこともある。。
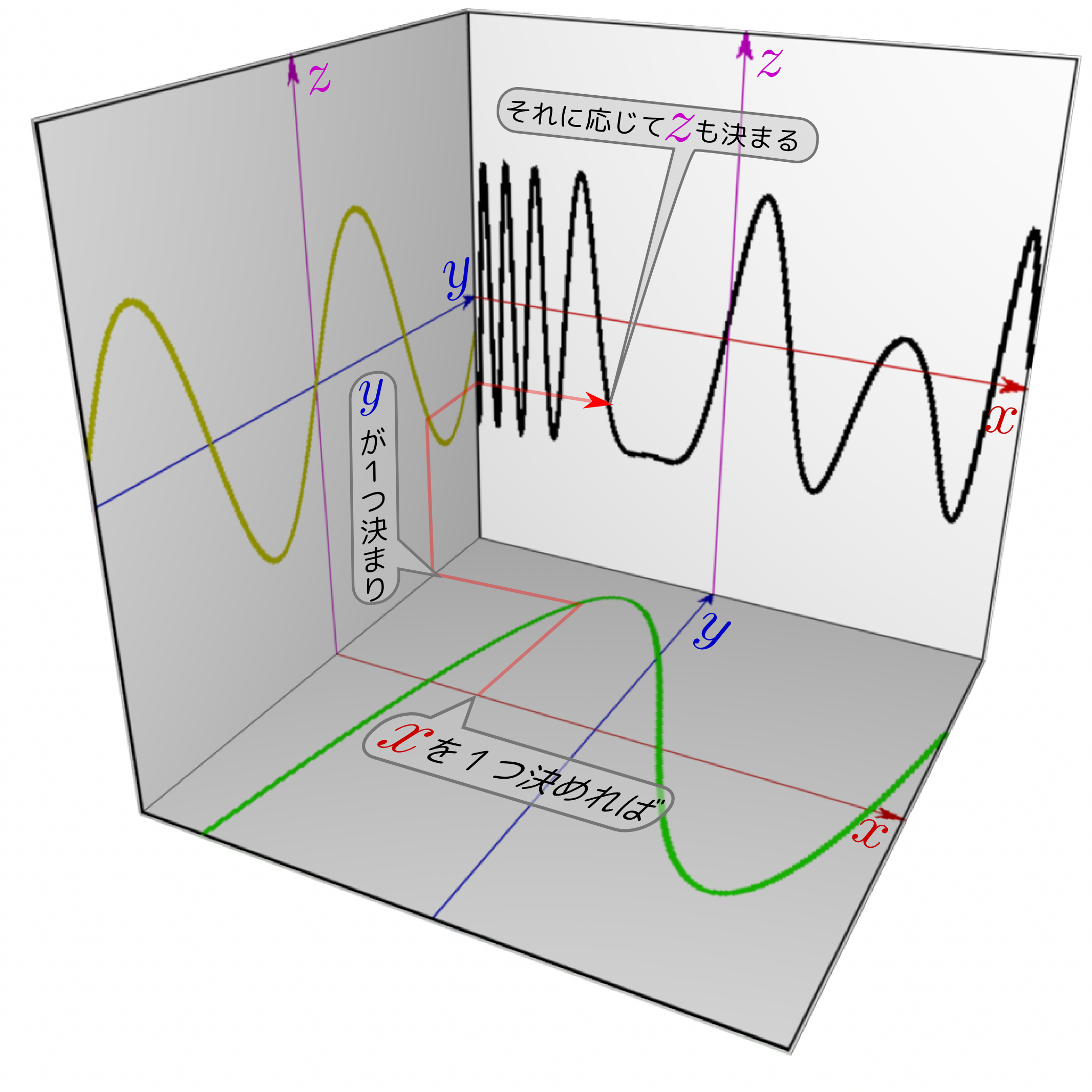
図は
$f({x})={x}^3-{x}^2-2{x}+1$
$g({y})=\sin 3{y}$
の場合で、この時、
\begin{equation} {z}=g(f({x}))= \sin \left(3({x}^3-{x}^2-2{x}+1)\right) \end{equation}ということになるyの変化の激しいところでは合成関数の結果であるzが激しく振動する、という様子が見て取れる。。
合成関数の定義域と値域には注意する必要がある。たとえば上にあげた例(${y}=1-{x^2}$と${z}=\sqrt{{y}}$を合成して${z}=\sqrt{1-{x}^2}$)の場合、${y}=1-{x^2}$だけを見ればxはどんな実数でもよさそう(定義域を$-\infty<{x}<\infty$としてもよさそう)に見えるが、その後で${z}=\sqrt{{y}}$という式にこの答えであるyが代入されることを思えば、$-1\leq{x}\leq 1$という定義域にしておかないと、${z}=\sqrt{1-{x}^2}$という関数が定義されてないことになる(虚数を含めれば話は別であるが)。
下に、動かせる合成関数の図をつける。
ここでは、
y=xという関数と
z=yという関数が合成され、
z=(x)という関数になっている。
◆や◆や◆のような形が走り回っているが、これはx,y,zの変化を表したものである。
- y=x2とz=
を合成すると、z=1
y1
x2 - y=x2とz=exp(-y)を合成すると、z=exp(-x2)
- y=sin(x)とz=y2を合成すると、z=sin(x)2
のように関数が合成されるところを確認しよう(もちろん他にももっといろいろなパターンがあるので、試してみよう)。
コンピュータにグラフを描かせる時の注意
たとえば、
| 1 x |
| 3 x |
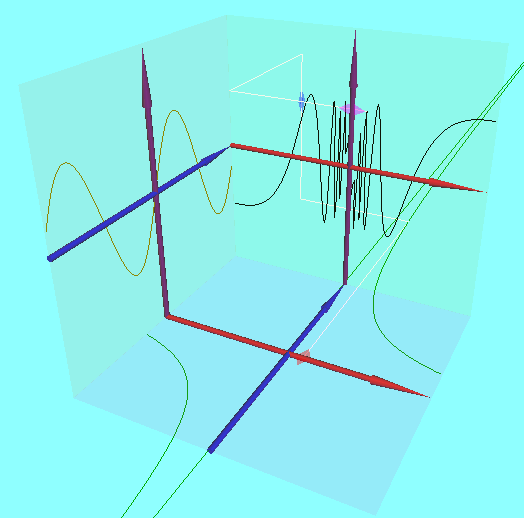
のようになる。このx=0付近のぐしゃっとなっているところ は、実は無限回の振動が隠れているなぜ無限回振動するのか、考えてみよう!。しかしコンピュータの画面も内部での計算でも「無限回の振動」を表すようにはできていない。実際にはxを0.01とか0.02とか、小さなステップで増加させては線を引く、というのを繰り返している。そのステップとステップの間に関数が激しく振動してしまうと、描かれたグラフは正確なものにはならないのである。
は、実は無限回の振動が隠れているなぜ無限回振動するのか、考えてみよう!。しかしコンピュータの画面も内部での計算でも「無限回の振動」を表すようにはできていない。実際にはxを0.01とか0.02とか、小さなステップで増加させては線を引く、というのを繰り返している。そのステップとステップの間に関数が激しく振動してしまうと、描かれたグラフは正確なものにはならないのである。
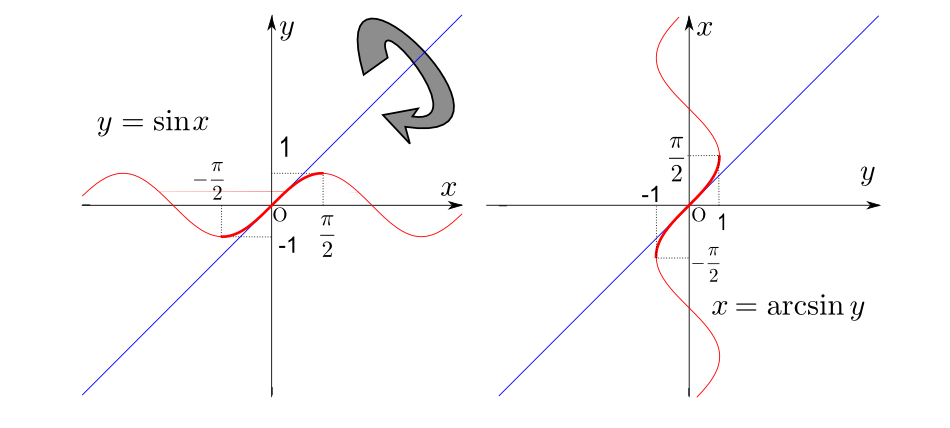
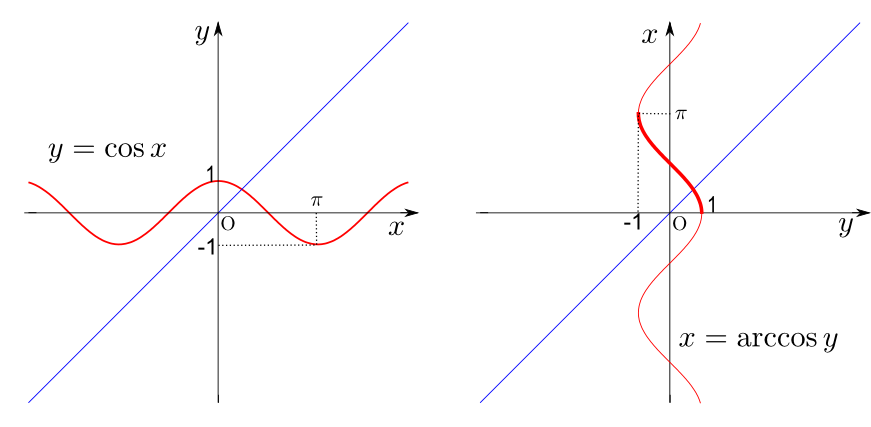
逆関数のペア
これらの関数は互いに逆関数になっているペアがある。それらを確認しよう。
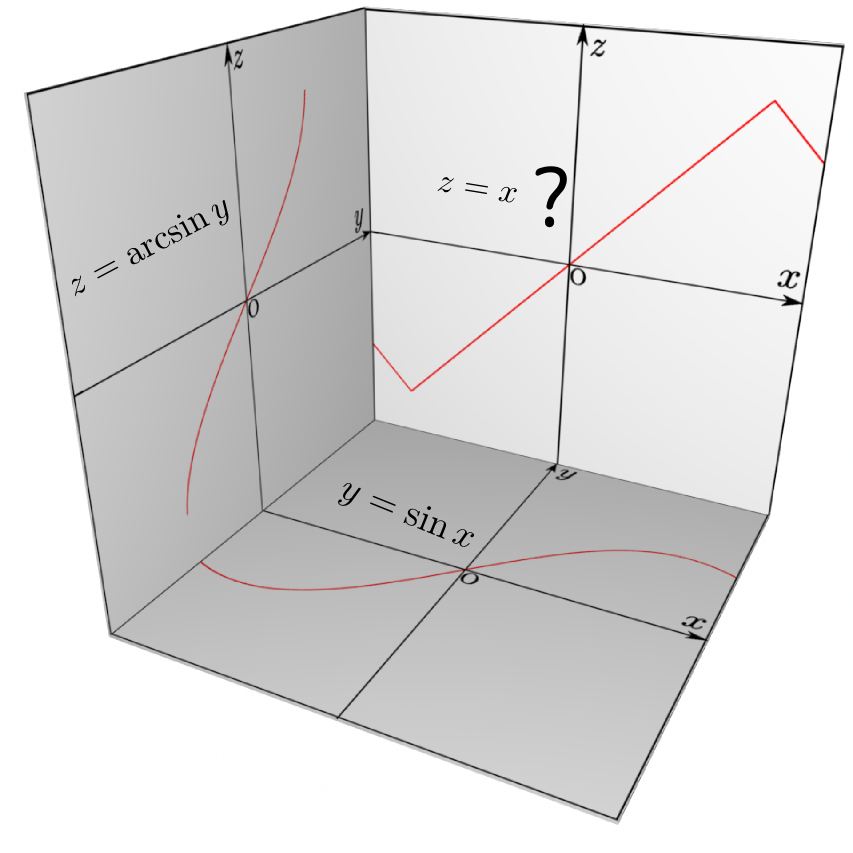
上の図ではx→y→zという合成関数を考えているが、2個めのy zが1個めのx yの逆関数であるので、x→y→xというつながりで元に戻ってくる。
よって、正しく逆関数になっていれば、z=xになるはずだ。
- y=axの逆関数はx=by(ただし、a=
)。1
b - y=
の逆関数はx=a
x
。a
y - y=x2の逆関数はx=√(
)|y|
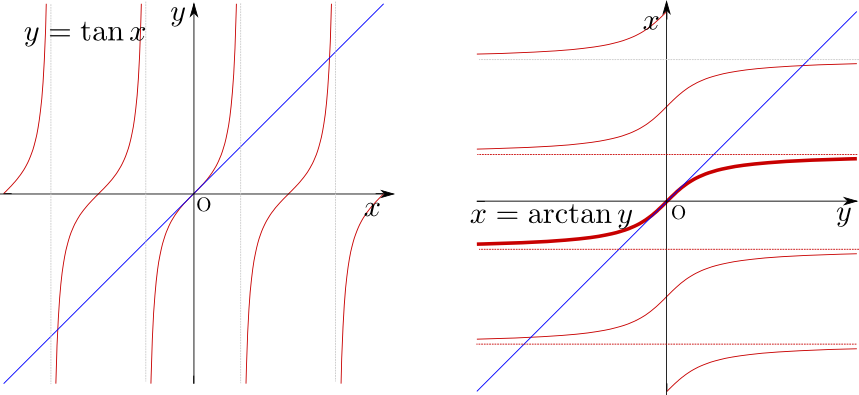
a - y=sin(ax)の逆関数はx=
arcsin(y)
a - y=exp(ax)の逆関数はx=log(
)|y|
a
ただし、実際やってみるとわかるように、これらは全てがちゃんとした逆関数にはなっていない。たとえばy=x2という関数はxが正でも負でも結果のyは正になる。そして、x=√|y|)の結果はどちらにしろ正の数になる。よって、x<0である状況では「xの符号を外す(絶対値を取る)」ということをしてしまって、逆関数にならないじゃあどうなるか、は上で確認すべし!。
同じような状況が他の場合でも起こり、上の例が逆関数になっていると言ってよいxの範囲は制限されることになる。これも、確認しよう。