テイラー展開(続き)
三角関数のテイラー展開
$\sin \xcol{x}$を例にして考えよう。すでに述べたように、$\sin \xcol{x}$は$\xcol{x}=0$で0であり、傾き1である。よって$\sin \xcol{x} \fallingdotseq \xcol{x}$と書けるのであった。$\sin \xcol{x}$の一階微分は$\cos \xcol{x}$、二階微分は$-\sin \xcol{x}$である。三階微分は$-\cos \xcol{x}$となり、微分するごとに$\sin \xcol{x}\to\cos\xcol{x}\to -\sin\xcol{x}\to -\cos\xcol{x}\to \sin \xcol{x}$と4つの関数をぐるぐる回る。
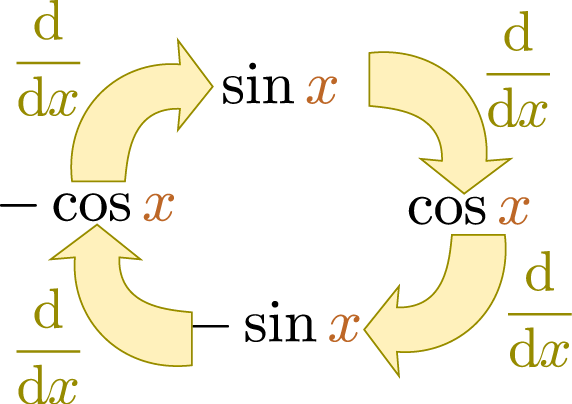
分類すれば、 \begin{equation} \left(\ddx\right)^n \sin \xcol{x}= \begin{cases} \sin\xcol{x}& n=4m\\ \cos\xcol{x}& n=4m+1\\ -\sin\xcol{x}& n=4m+2\\ -\cos\xcol{x}& n=4m+3 \end{cases}~~~(mは0以上の整数)\label{sindiffn} \end{equation} であり、これに$\xcol{x}=0$を代入すれば \begin{equation} \left(\ddx\right)^n \sin \xcol{x} \biggr|_{\xcol{x}=0}= \begin{cases} 0& n=2m\\ 1& n=4m+1\\ -1& n=4m+3 \end{cases}~~~(mは0以上の整数)\label{sinexpcof} \end{equation} ($n=4m$と$n=4m+2$は一つにまとめて$n=2m$とした)であるから、 \begin{equation} \sin \xcol{x}=\xcol{x} - {\xcol{x}^3\over 3!}+ {\xcol{x}^5\over 5!}-{\xcol{x}^7\over 7!}+\cdots\label{sintaylor} \end{equation} のようにテイラー展開できる偶数次の項が出てこないのが$\sin$の特徴であるが、$\sin$に限らず奇関数なら常に奇数次しか出てこない。ただし、$\xcol{x}=0$以外で展開した場合はこの限りではない。。
テイラー展開が近づいていく様子は、アプリを参照せよ。
一方、同様の計算をやると$\cos\xcol{x}$の方は \begin{equation} \cos \xcol{x}=1 - {\xcol{x}^2\over 2!}+ {\xcol{x}^4\over 4!}-{\xcol{x}^6\over 6!}+\cdots\label{costaylor} \end{equation} のようにテイラー展開できる($\cos$では奇数次の項が出てこない偶関数のテイラー展開では常に、偶数次の項のみが出てくる。)。
テイラー展開が近づいていく様子は、アプリを参照せよ。
$\exp$の展開と、$\sin $の展開式と$\cos $の展開式をよく見ると、 \begin{equation} \begin{array}{ccccccccc} \E^{\xcol{x}}= &1 &+\xcol{x} &+{\xcol{x}^2\over 2!} &+{\xcol{x}^3\over 3!} &+{\xcol{x}^4\over 4!} &+{\xcol{x}^5\over 5!} &+{\xcol{x}^6\over 6!} &+\cdots \\[3mm] \cos \xcol{x}= &1 & &-{\xcol{x}^2\over 2!} & &+{\xcol{x}^4\over 4!} & &-{\xcol{x}^6\over 6!} &+\cdots \\ \sin \xcol{x}= & &\xcol{x} & &-{\xcol{x}^3\over 3!} & &+{\xcol{x}^5\over 5!} & &+\cdots \\ \end{array}\label{Eulercossin} \end{equation} となっている。ここで「$\cos\xcol{x}$と$\sin\xcol{x}$の展開は$\E^{\xcol{x}}$に似ているが、符号が一項ごとに反転するのが惜しいな」と気づく。$\E^{\xcol{x}}$の展開で2項ごとに符号が反転してくれれば同じものになりそうだ。そうするためには、 \begin{equation} \begin{array}{cccccccccl} \E^{\xcol{x}}= &1 &+\xcol{x} &+{\xcol{x}^2\over 2!} &+{\xcol{x}^3\over 3!} &+{\xcol{x}^4\over 4!} &+{\xcol{x}^5\over 5!} &+{\xcol{x}^6\over 6!} &+\cdots &~~~~~{\xcol{x}\to \I\xcol{x}と置き換えて}\\[3mm] \E^{\I \xcol{x}}=& 1 &+\I \xcol{x} &-{\xcol{x}^2\over 2!} &-\I{\xcol{x}^3\over 3!} &+{\xcol{x}^4\over 4!} &+\I{\xcol{x}^5\over 5!} &-{\xcol{x}^6\over 6!} &+\cdots \end{array} \end{equation} のように指数に虚数単位$\I$をつければよい($\xcol{x}\to\I\xcol{x}$と置き換えればよい)と気がつけば、 \begin{equation} \E^{\I \xcol{x}}=\cos \xcol{x}+\I \sin \xcol{x}\label{Euler} \end{equation} という「オイラーの関係式」が見えてくる。
テイラー展開可能な点と不可能な点
テイラー展開が可能であるためには、$f\kakko{x_0}$はもちろん、任意の階数の微係数$\ddx f\kakko{x_0},\left(\ddx\right)^2f\kakko{x_0},\cdots$が全て計算できなくてはいけない。たとえば、$f\kakko{\xcol{x}}=\sqrt{\xcol{x}}$を$\xcol{x}=0$の回りにテイラー展開することはできない(この関数は$\xcol{x}=0$において解析的でない)。$\ddx f\kakko{\xcol{x}}={1\over 2\sqrt{\xcol{x}}}$なので、$\xcol{x}=0$では微分が存在しない(あえて書くなら$\infty$)。グラフでは、$\xcol{x}=0$において線が垂直に立っていることで「微分できない」ことが表現されている。
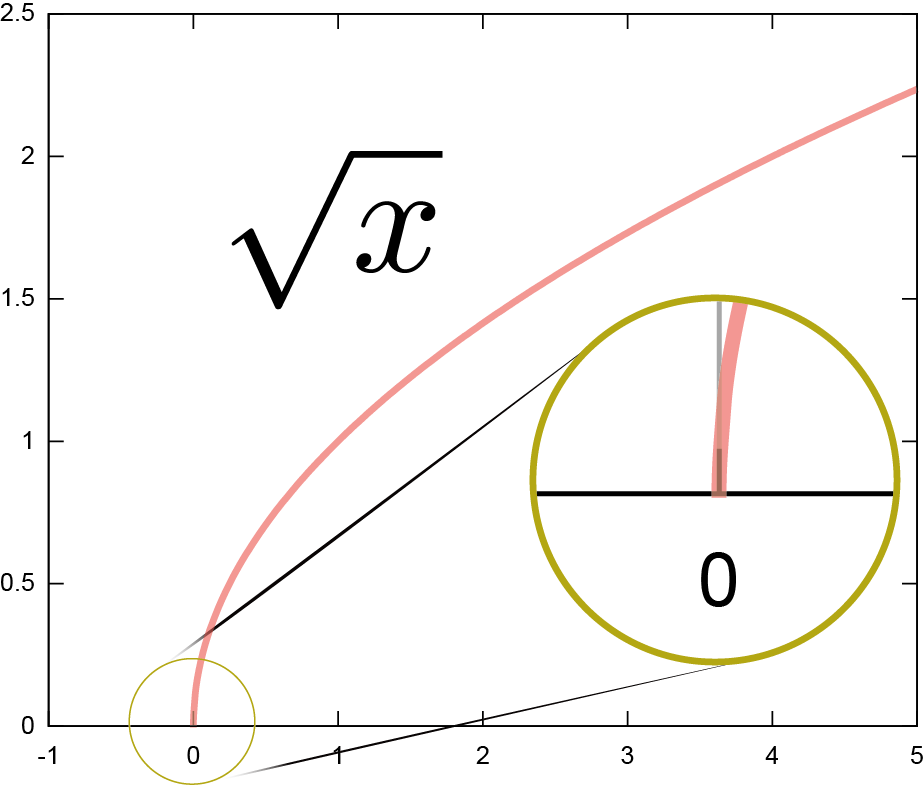
では$\sqrt{\xcol{x}}$のような関数はどうやって近似するかというと、$\xcol{x}=0$以外、たとえば$\xcol{x}=1$の回りにテイラー展開する。$\xcol{x}=1$でなら、${1\over 2\sqrt{\xcol{x}}}\biggr|_{\xcol{x}=1}={1\over 2}$となって値がある。二階微分も計算しておくと、$\left(\ddx\right)^2\sqrt{\xcol{x}}=-{1\over 4\xcol{x}^{3\over 2}}$となるから2次の項の係数は${1\over 2}\left(\ddx\right)^2\sqrt{\xcol{x}}\biggr|_{\xcol{x}=1}=-{1\over 8}$であり(3次以上の項については詳細は省くが同様の計算を行って)、 \begin{equation} \sqrt{\xcol{x}}= 1 +{1\over 2}(\xcol{x}-1)-{1\over 8}(\xcol{x}-1)^2+{1\over 16}(\xcol{x}-1)^3-{5\over 128}(\xcol{x}-1)^4+\cdots \end{equation} のように展開できる。たとえば電卓を叩けば$\sqrt{1.2}\fallingdotseq1.09544511501033\cdots$という式が出るが、電卓内部では上のような展開を使って計算される。やってみると、 \begin{equation} \sqrt{1.2}= \underbrace{\underbrace{\underbrace{\underbrace{1 +\underbrace{{1\over 2}(1.2-1)}_{0.1}}_{1.1}-\underbrace{{1\over 8}(1.2-1)^2}_{0.005}}_{1.095}+\underbrace{{1\over 16}(1.2-1)^3}_{0.0005}}_{1.0955}-\underbrace{{5\over 128}(1.2-1)^4}_{0.0000625}}_{1.0954375}+\cdots \end{equation} のようにして正しい値に近づいていく。アプリを参照せよ。