前期の復習:常微分方程式
今日はまず、プログラムを使って微分方程式のイメージをつかんでもらいました。
常微分方程式の復習
「常微分方程式(ordinary differential equation)」とは、独立変数$\xcol{x}$、従属変数$\ycol{y}$と、その微分$\ddx \ycol{y},\dtwodx\ycol{y},\cdots$の間にある \begin{equation} \Phi\left(\xcol{x},\ycol{y},\ddx \ycol{y},\dtwodx\ycol{y},\cdots\right)=0 \end{equation} のような形で書ける関係式($\Phi$は任意の関数)である。
この式を満たす$\ycol{y}$と$\xcol{x}$の関係を($\ycol{y}=f\kakko{\xcol{x}}$などのような形で)求めることを「微分方程式を解く」と言う。グラフで考えると一階微分$\ddx \ycol{y}$は傾きを、二階微分$\dtwodx\ycol{y}$は曲がり具合を表現している。つまり微分方程式は「ある場所$(\xcol{x},\ycol{y})$での局所的(local)な情報」の間の関係式である。一方、関数$\ycol{y}=f\kakko{\xcol{x}}$を与えると、二つの変数の間の関係を大域的(global)に与える。微分方程式を解くというのは局所的情報から大域的情報を導くことであるとも言える(逆に微分は、大域的情報から局所的情報を得る)。
一階微分方程式と解曲線
1変数の微分方程式この場合の「1変数」とは「独立変数が一つ」という意味。を「常微分方程式」と呼ぶ。ここでは一階の常微分方程式 \begin{equation} {\coldy\over \coldx}=g\,\kakko{\xcol{x},\ycol{y}}\label{ikkaide} \end{equation} を考える。グラフでは、左辺の${\coldy\over \coldx}$は「$\ycol{y}=f\kakko{\xcol{x}}$曲線の傾き」であるから、上の式は「$\ycol{y}=f\kakko{\xcol{x}}$を表すグラフの曲線の傾きは$g\,\kakko{\xcol{x},\ycol{y}}$である」と読み取ることができる。
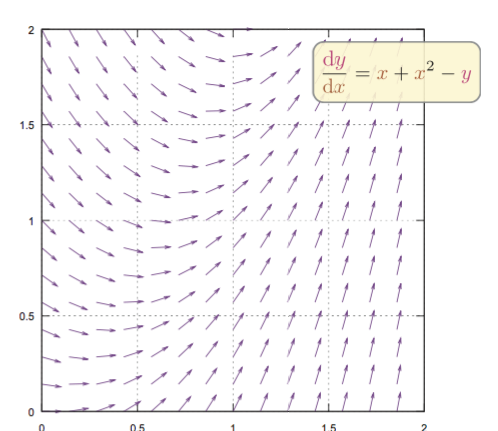
上の図は$g\,\kakko{\xcol{x},\ycol{y}}=\xcol{x}+\xcol{x}^2-\ycol{y}$である場合の各点各点での${\coldy\over \coldx}$を矢印で示したものである。 二つの変数$\xcol{x},\ycol{y}$の間には関数$\ycol{y}=f\kakko{\xcol{x}}$という関係があるが、最初はその関数は求まっておらず、${\coldy\over \coldx}=g\,\kakko{\xcol{x},\ycol{y}}$だけがわかっている。これはつまり、$(\xcol{x},\ycol{y})$の各点での「傾き」だけが決っているという状況である。
微分方程式を解くことによって各点を通る線がどのようにつながっていくかがわかる(上の例の場合ならば、下の図のような答えが出てくることになる)。この曲線は1本ではなく、平面を埋め尽くす「埋め尽くす」と言ったが、考えている式の定義域や値域から外れる部分はもちろん埋め尽くせない(${\coldy\over \coldx}=\sqrt{1-\xcol{x}^2}$の$\xcol{x}^2>1$の範囲など)。ように引くことができる(よって「曲線群」と呼ぼう)。
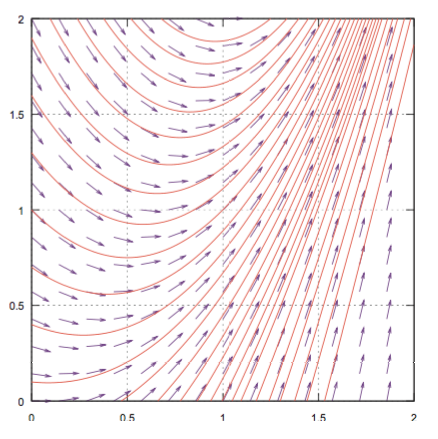
微分方程式の解を求めるというのはこの曲線群を求めることである。さらになんらかの「境界条件」を置くことでこの曲線の中から1本を選ぶ。結果として一つの関数$\ycol{y}=f\kakko{\xcol{x}}$が決まる。これで$\ycol{y}$は従属変数となり、自由に決めることができる変数(独立変数)は$\xcol{x}$のみになった。独立変数が一つであることを「自由度(degree of freedom)が1」と表現する。図形の上で「自由度1」は「線」である(後で出てくる「自由度2」は面である)。
こうして(まだどうやって求めたかは説明してないが)求められた関数の表す曲線を「解曲線」と呼ぶ。
では、具体的に解曲線を求める例を考えよう。
$g\,\kakko{\xcol{x},\ycol{y}}=\xcol{x}$を考える。この式は両辺を積分することによって \begin{equation} \begin{array}{rl} {\coldy\over \coldx}=&\xcol{x}\\ \ycol{y}=&{\xcol{x}^2\over 2}+C~~(Cは積分定数) \end{array} \end{equation} となる。解曲線群は次の図のようになる。
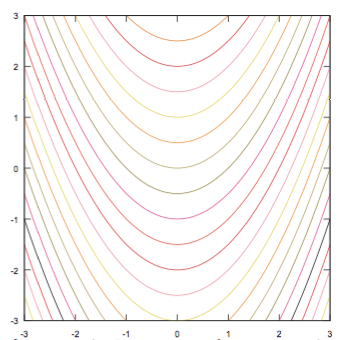
ここで、積分を行ったことにより積分定数という「未定のパラメータ」が解に入り込んだことに注意しよう。このパラメータ(積分定数)のおかげで解は1本の曲線ではなく曲線群となる。
このように$g\,\kakko{\xcol{x},\ycol{y}}$が簡単に積分できるようなら簡単だが、一般にはもちろんそうはいかない。もし$g\,\kakko{\xcol{x},\ycol{y}}$が$\xcol{x}$の関数と$\ycol{y}$の関数の積の形で書けているならば、 \begin{equation} {\coldy\over \coldx}=m\kakko{\xcol{x}} n\kakko{\ycol{y}}~~~~\rightarrow~~~~{\coldy\over n\kakko{\ycol{y}}}=m\kakko{\xcol{x}}\coldx \end{equation} のように、左辺に$\ycol{y}$を、右辺に$\xcol{x}$をと「変数分離」することができて解くことができる。変数分離で解くことができるもう一つの簡単な例として、 \begin{equation} {\coldy\over \coldx}=-{1\over K}{\xcol{x}\over \ycol{y}} \end{equation} を考えよう(次の図はこの式が示す傾きを描いたもので、$K=2$の場合である)。
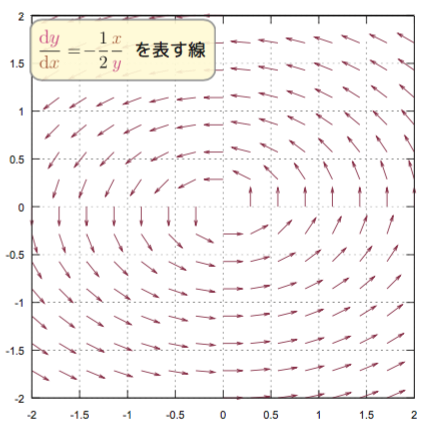
変数分離すると、 \begin{equation} \ycol{y}\coldy=-{1\over K}\xcol{x}\coldx \end{equation} であり、両辺を積分することで \begin{equation} {1\over 2}\ycol{y}^2 = -{1\over 2K}\xcol{x}^2 +C \end{equation} となる。
この式は整理すると \begin{equation} {\xcol{x}^2\over {2CK}}+{\ycol{y}^2\over 2C}=1 \end{equation} となるから、長径が$\sqrt{2CK}$、短径が$\sqrt{2C}$である楕円$K>1$ならこうだが、$K<1$ならば$\sqrt{2CK}$の方が短径になる。$K=1$なら円である。となる。 微分方程式を解くとは、このように傾きから関数全体の形を導き出すことである。
この場合も、積分定数$C$のおかげで様々な長短径を持つ楕円が現れたこと(解曲線である楕円が1個の未定パラメータを持ったこと)に注意しよう。1階微分方程式を解くと必ずこのような未定パラメータが出てくる。これはその解き方が本質的に「不定積分する」ことであり、その結果としての積分定数を答えが含むことになるからである。二階以上の微分方程式では階数に応じて積分を行うことで解を得るので、$n$階微分方程式の解は$n$個の未定パラメータを含むと言える。
楕円の例は変数分離ができたが、すべての微分方程式が変数分離できるわけではない。また変数分離できたとしてもその結果が積分できる関数になっているかどうかはわからないので、「どんな微分方程式でも解ける方法」は残念ながら存在しない。というより実は「解析的に解けない微分方程式」変数分離などの方法を使って積分して解く方法を「解析的に解く」という言い方をする。の方が圧倒的に多いのである。解析的に解けない微分方程式は、近似を使って解く、コンピュータに頼って数値計算で解く、などの方法がある。
線形常微分方程式
「線形常微分方程式」とは、求めたい関数$\ycol{y}=f\kakko{\xcol{x}}$とその微分(微分の階数は何階でもよい)に関して1次以下の式のみを含む常微分方程式である。特に$\ycol{y}$の0次(これは定数という意味ではなく、$\xcol{x}$の関数であっても「$\ycol{y}$の0次」である)を含まない場合を「線形斉次」、含む場合を「線形非斉次」と呼ぶ。
$n$階の線形非斉次微分方程式は \begin{equation} \left( A_n\kakko{\xcol{x}}\left(\ddx\right)^n +A_{n-1}\kakko{\xcol{x}}\left(\ddx\right)^{n-1} +\cdots +A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}} \right)\ycol{y} =C\kakko{\xcol{x}} \end{equation} と書くことができる。
線形斉次方程式は、$C\kakko{\xcol{x}}=0$とした、 \begin{equation} \left( A_n\kakko{\xcol{x}}\left(\ddx\right)^n +A_{n-1}\kakko{\xcol{x}}\left(\ddx\right)^{n-1} +\cdots +A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}} \right)\ycol{y} =0 \end{equation} である。
この式の応用として面白いのは、以下の事実である。
線形斉次微分方程式の重ね合わせ
線形斉次方程式の解を$y_1\kakko{\xcol{x}}$と$y_2\kakko{\xcol{x}}$と二つ見つけたとすれば、この二つの和である$y_1\kakko{\xcol{x}}$と$y_2\kakko{\xcol{x}}$も解である。
これを数式で確認しておこう。$\left( A_n\kakko{\xcol{x}}\left(\ddx\right)^n +\cdots +A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}} \right)={\cal D}$と書くことにすると、 \begin{equation} \small\begin{array}{rlll} & {\cal D}y_1\kakko{\xcol{x}} &=0\\ & {\cal D}y_2\kakko{\xcol{x}} &=0\\ \hline & {\cal D}(y_1\kakko{\xcol{x}}+y_2\kakko{\xcol{x}})&=0 \end{array}\label{ConeCtwo} \end{equation} となる。
といえる。
ここで使った「線形結合」という言葉について。単純に言えば○○の線形結合とは変数の組○○から、定数倍と足算によって作られる量になる。$\xcol{x}$と$\ycol{y}$を掛けたり割ったりしてはいけない(自乗もダメ)$-1$倍して足すという計算も含まれるので、引算も含まれていることに注意。。
$\xcol{x},\ycol{y},\cdots$の線形結合で表される$\zcol{z}=a\xcol{x}+b\ycol{y}+\cdots$があったとすると、「$\zcol{z}$は$\xcol{x},\ycol{y},\cdots$と線形独立(linearly independent)ではない」「線形独立ではない」ことを「線形従属」と表現することもある。これらの用語も「1次独立」「1次従属」という言い方もある。という言い方をする。逆に「$\xcol{x},\ycol{y},\zcol{z}$が線形独立である」とは $\xcol{x}$と$\ycol{y}$をどのように「定数倍して足したり引いたり」しても、$\zcol{z}$にはならない($\xcol{x},\ycol{y},\zcol{z}$の組合せを変えたものについても同様)ということである(この表現の方が「独立」の意味がわかりやすい)。
たとえば\文中式{$f_1\kakko{\xcol{x}}=\xcol{x},f_2\kakko{\xcol{x}}=\xcol{x}^2$}に対し{$f_3\kakko{\xcol{x}}=2\xcol{x}^3$とすると、定数$a,b$をどのように選んでも全ての$\xcol{x}$の定義域で\文中式{$f_3\kakko{\xcol{x}}=af_1\kakko{\xcol{x}}+bf_2\kakko{\xcol{x}}$}が成立するようにすることはできないから、$f_3\kakko{\xcol{x}}$は$f_1\kakko{\xcol{x}},f_2\kakko{\xcol{x}}$と線形独立である。
一方、$f_1\kakko{\xcol{x}}=\cos\xcol{x},f_2({\xcol{x}})=\sin\xcol{x}$とすると、$f_3\kakko{\xcol{x}}=\cos\kakko{\xcol{x}+{\pi\over4}}$}は$f_1,f_2$の適切な線形結合で表せる(三角関数の加法定理を使えば示せる)から、$f_3\kakko{\xcol{x}}$は$f_1\kakko{\xcol{x}},f_2\kakko{\xcol{x}}$に線形従属である。
ここで、上で述べた「$n$階微分方程式は$n$個のパラメータを含む」ということと結びつけると面白いことがわかる。