線形微分方程式

$\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{{↓#1}}\def\goverbrace{\overbrace}$

　前回で、線形微分方程式の性質、特に重ね合わせの原理について考えた。

非斉次の場合の重ねあわせ

　非斉次の場合、つまり$\ycol{y}$の1次のみではなく$\ycol{y}$の0次の項がある線形微分方程式 \begin{equation} \left( A_n\kakko{\xcol{x}}\left(\ddx\right)^n +A_{n-1}\kakko{\xcol{x}}\left(\ddx\right)^{n-1} +\cdots +A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}} \right)\ycol{y} =C\kakko{\xcol{x}} \end{equation} の解を考えてみる。右辺においた、線形非斉次微分方程式の0次の項$C\kakko{\xcol{x}}$（$\ycol{y}$を含んではいけないが、$\xcol{x}$の関数であってもよい）のことを「ソースターム（source term）」あるいは単に「源」または「ソース」と呼ぶ。話し言葉では「ソース」と呼ぶことが多い。このように呼ぶ理由は、このような方程式が「$C\kakko{\xcol{x}}$という量が$\ycol{y}\kakko{\xcol{x}}$を作り出す」という法則を表現することが多いからである。たとえば「ストーブがあるとまわりは温度が高い」「質量があるとまわりに重力場ができる」「電荷があるとまわりに電場ができる」などの場合「ストーブ」「質量」「電荷」が\ruby{源}{ソース}である（こういう現象も微分方程式で表現できるのだ）。この式の応用として面白いのは、以下の事実である。

　これを数式で確認しておこう。 \begin{equation} \begin{array}{rlll} & \left(A_n\kakko{\xcol{x}}\left(\ddx\right)^n+\cdots+A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}}\right)y_1\kakko{\xcol{x}} &=C_1\kakko{\xcol{x}}\\ & \left(A_n\kakko{\xcol{x}}\left(\ddx\right)^n+\cdots+A_1\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}} \right)y_2\kakko{\xcol{x}} &=C_2\kakko{\xcol{x}}\\ \hline & \left(A_n\kakko{\xcol{x}}\left(\ddx\right)^n+\cdots+A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}}\right)(y_1\kakko{\xcol{x}}+y_2\kakko{\xcol{x}})&=C_1\kakko{\xcol{x}}+C_2\kakko{\xcol{x}}\\ \end{array} \end{equation} となる「$C_1\kakko{\xcol{x}}$を源とする解」と「$C_2\kakko{\xcol{x}}$を源とする解」の線形結合の場合に拡張すれば、「$\alpha_1 C_1\kakko{\xcol{x}}+\alpha_2 C_2\kakko{\xcol{x}}$を源とする解」を作ることもできる。上の場合、$\alpha_1=\alpha_2=1$の場合である。$\alpha_1=1,\alpha_2=-1$にすれば「差」になる。}。次のようなことも言える。

　非斉次方程式 \begin{equation} \left( A_n\kakko{\xcol{x}}\left(\ddx\right)^n +A_{n-1}\kakko{\xcol{x}}\left(\ddx\right)^{n-1} +\cdots +A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}} \right)\ycol{y}=C\kakko{\xcol{x}}\label{hiseijirei} \end{equation} と、上の式で$C\kakko{\xcol{x}}=0$とした斉次方程式 \begin{equation} \left( A_n\kakko{\xcol{x}}\left(\ddx\right)^n +A_{n-1}\kakko{\xcol{x}}\left(\ddx\right)^{n-1} +\cdots +A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}} \right)\ycol{y} =0 \end{equation} を考える。非斉次方程式の解として$y_1\kakko{\xcol{x}}$を１つ、斉次方程式の解として$y_0\kakko{\xcol{x}}$を１つ、それぞれ見つけたとする。${y_0}\kakko{\xcol{x}}+y_1\kakko{\xcol{x}}$もまた、非斉次方程式の解である。

　これは上で考えたことの$C_2\kakko{\xcol{x}}=0$の場合にあたるから、証明は不要だろう。わざわざこんな（言わば、「あたりまえ」の）ことをここに書いたのは、この事実は応用範囲が広いからである。というのは、斉次方程式と非斉次方程式では当然斉次方程式の方が解きやすい。非斉次方程式の方の解は一つだけ求めておいて、斉次方程式の解を見つけられる限り見つけておけば、重ねあわせによって非斉次方程式の解をたくさん（見つけられる限り）見つけることができるようになる。

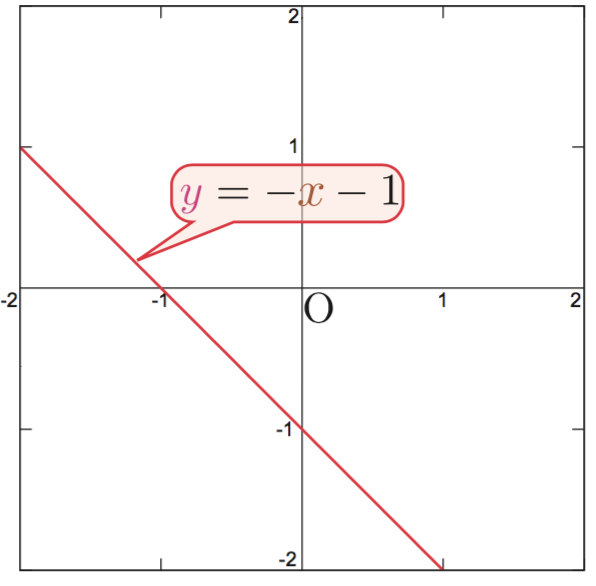
　簡単な例をやってみよう。$\ddx \ycol{y}= \xcol{x}+\ycol{y}$という線形非斉次微分方程式を解きたい。これは「変数分離できる形」にはなってない。そこで試行錯誤で解を探す。たとえば$\ycol{y}=a\xcol{x}+b$が解になるだろうか、と考え代入してみると、 \begin{equation} \begin{array}{rl} \goverbrace{a}^{\tiny \ddx \ycol{y}}=& \xcol{x}+\goverbrace{a\xcol{x}+b}^{\ycol{y}} \\ 0=&(1+a)\xcol{x}+b-a \end{array} \end{equation} となるから、$a=-1,b=-1$にすれば解となる。

　ゆえに、$\ycol{y}=-\xcol{x}-1$という解が見つかったわけだが、ここで「バンザイ、解が見つかった」と終わってはいけない。なぜなら関数$\ycol{y}=-\xcol{x}-1$は下のグラフであり、この線の上という（全$\xcol{x}$-$\ycol{y}$平面から見たらほんとに狭い）範囲の上での「解」を求めたに過ぎない。

　この解は前に述べた特解であり、我々が求めたいのは全$\xcol{x}$-$\ycol{y}$平面を埋め尽くす、一般解である。

非斉次になっているのは$\xcol{x}$という項のせいだから、これを消して$\ddx \ycol{y}= \ycol{y}$という斉次方程式を作る。この方程式の解は、何度も出てきているお馴染みの$\ycol{y}=C \E^{\xcol{x}}$である。非斉次方程式の解は特解にこの斉次方程式の一般解を足せば作ることができる。

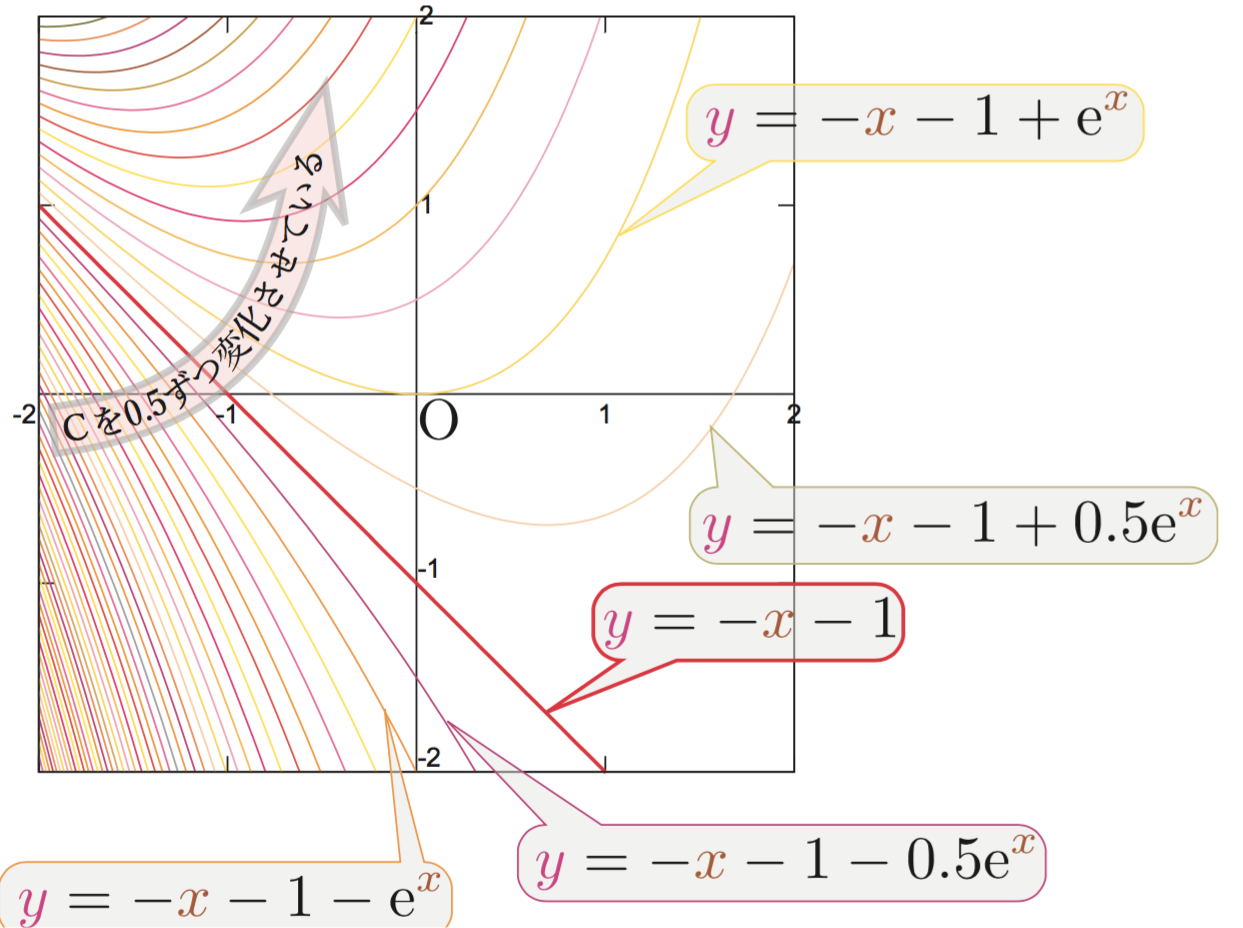
　すなわち、一般解は \begin{equation} \ycol{y}=-\xcol{x}-1 + C\E^{\xcol{x}}\label{seijiippankai} \end{equation} となる。$C$を$0.5$ずつ変えた線を示すグラフが次の図である。

　描かれている線と線の隙間にも線があり、解の曲線は全平面を埋め尽くし埋め尽くしていることを確認するには、任意の点の座標$(\xcol{x},\ycol{y})=(x_0,y_0)$を代入すると必ず一つ$C$が決まることを見る。この場合なら、$C=(y_0+x_0+1)\E^{-x_0}$である。微分方程式の形によっては解の曲線が通らない領域が存在することもあり得る（例えば、${\coldy\over \coldx}=\sqrt{1-\xcol{x}^2}$は$|\xcol{x}|>1$では解がない）。、どのような初期値$(x_0,y_0)$から出発しても、微分方程式に従うその後の変化がわかる。重ねあわせの原理のおかげで以上のような計算ができる。

　以上で「線型非斉次微分方程式の一般解を求める」という問題は、

• 「線形斉次微分方程式の一般解」を求める。
• 「線形非斉次微分方程式の特解」を求める。

の二段階に分けられることがわかった。

定数係数の線形斉次微分方程式

　一般的な線形斉次微分方程式の解き方を考える前に、線形斉次で、かつ係数$A_i\kakko{\xcol{x}}$が定数$A_i$である場合、すなわち \begin{equation} \left( A_n\left(\ddx\right)^n +A_{n-1}\left(\ddx\right)^{n-1} +\cdots +A_{1}{\ddx} +A_0 \right)\ycol{y} =0\label{teisuusenkeiseiji} \end{equation} の形の微分方程式を解く一般的な方法を示そう。

特性方程式

　まず、この微分方程式には、$\E^{\lambda \xcol{x}}$という形で表せる解がある（$\lambda$はこの後決める定数である）。これが解になるかどうかを確認するために代入してみると、 \begin{equation} {\ddx }\E^{\lambda\xcol{x}}=\lambda\E^{\lambda\xcol{x}},~~ \left({\ddx }\right)^2\E^{\lambda\xcol{x}}=\lambda^2\E^{\lambda\xcol{x}},\cdots, \left({\ddx }\right)^n\E^{\lambda\xcol{x}}=\lambda^n\E^{\lambda\xcol{x}} \end{equation} となることを使うと、微分方程式は \begin{equation} \left( A_n\lambda^n +A_{n-1}\lambda^{n-1} +\cdots A_1 \lambda + A_0 \right)\E^{\lambda\xcol{x}}=0 \end{equation} という式に変わる。よって、 \begin{equation} A_n\lambda^n +A_{n-1}\lambda^{n-1}+\cdots A_1 \lambda + A_0=0\label{tokusei} \end{equation} となるような$\lambda$が存在していれば、その$\lambda$を代入した$\E^{\lambda \xcol{x}}$が解である。$\lambda$が満たすべき方程式を「特性方程式」と呼ぶ。

　簡単な例として、特性方程式が二次方程式になる場合をやってみよう。

　$\left( \left(\ddx\right)^2-\ddx -2\right)f\kakko{\xcol{x}}=0$の解が$\E^{\lambda\xcol{x}}$だと仮定し代入すると、$\ddx\E^{\lambda\xcol{x}}=\lambda\E^{\lambda\xcol{x}}$,$\left(\ddx\right)^2\E^{\lambda\xcol{x}}=\lambda^2\E^{\lambda\xcol{x}}$を使って、 \begin{equation} \begin{array}{rccccl} \biggl(& \!\!\!\left(\ddx\right)^2 & \!\!-&\ddx&\!\!-2 \biggr)\E^{\lambda\xcol{x}}=0 \\[-1mm] & ↓ & &↓ & & \\[-3mm] \biggl(& \lambda^2& \!\!-&\lambda&\!\!-2 \biggr)\E^{\lambda\xcol{x}}=0 \end{array}\label{nijiex} \end{equation} という式が導かれ、特性方程式$\lambda^2-\lambda-2=0$が満たされれば$\E^{\lambda\xcol{x}}$が解になることがわかる。特性方程式は$(\lambda-2)(\lambda+1)=0$と因数分解できるので、$\lambda=2,\lambda=-1$の二つの解があり、 \begin{equation} f\kakko{\xcol{x}}=C\E^{2\xcol{x}}+D\E^{-\xcol{x}} \end{equation} のような重ねあわせが微分方程式の一般解であるとわかる。$\E^{2\xcol{x}}$と$\E^{-\xcol{x}}$が線形独立であることにも注意しよう。$n$階線型微分方程式は線形独立な解を$n$個見つければ、それで「$n$個のパラメータを持つ解」を作ることができる。

　二階微分方程式は二つの未定パラメータを持つ筈なので、これで解は求まっている。

　第1問の特性方程式は$\lambda^2+5\lambda+6=0$で、$\lambda=-2,-3$が解なので、微分方程式の解は $$ \ycol{y}=A\E^{-2\xcol{x}}+B\E^{-3\xcol{x}} $$

　第2問の特性方程式は$\lambda^3-\lambda=0$で、$\lambda=0,1,-1$が解なので、微分方程式の解は $$ \ycol{y}=A+B\E^{\xcol{x}}+C\E^{-\xcol{x}} $$ が解。定数解$A$を忘れないように（三階微分方程式だから三つの解が見つからないといけない）。

　ここでは特性方程式を出してから因数分解し$\lambda$を求めたが、$\left(\left(\ddx\right)^3-\ddx\right)\ycol{y}=0$を $$ \left(\left(\ddx\right)^2-1\right)\ddx\ycol{y}=0 $$ あるいはさらに $$ \left(\ddx+1\right)\left(\ddx-1\right)\ddx\ycol{y}=0 $$ と書き換えてもよい（いわば『微分演算子の因数分解』である）。

さて、これで線形斉次で定数係数の二階微分方程式は二次方程式を使って解くことができることがわかった。この方法で二つの解が求められると安心してよいか？？---実は注意が必要な点がある。一般の特性方程式$A_2\lambda^2+A_1\lambda+A_0=0$が二つの実数解を持つとは限らない、ということだ。ではそういう場合はどうするのか？---は来週やろう。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。