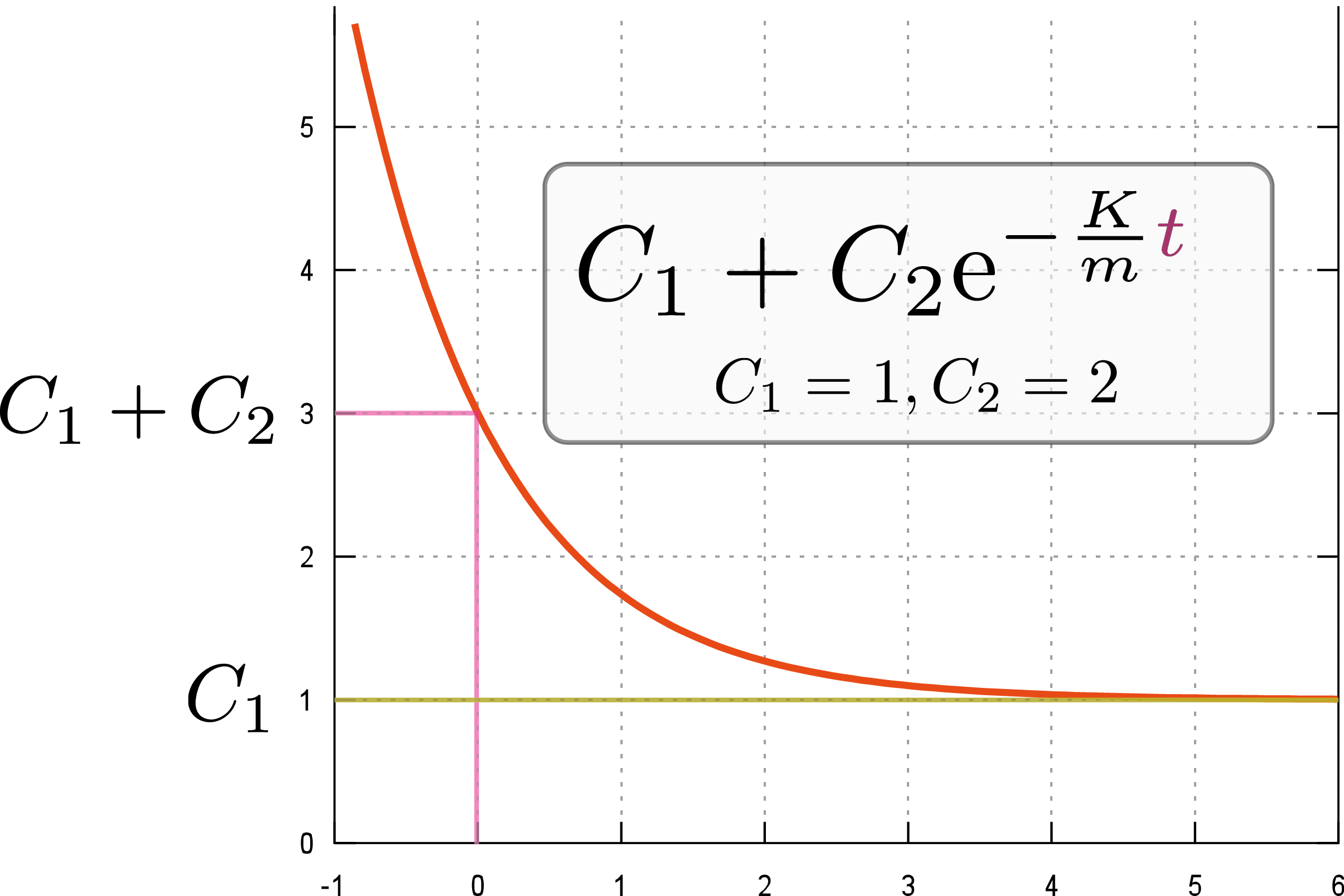
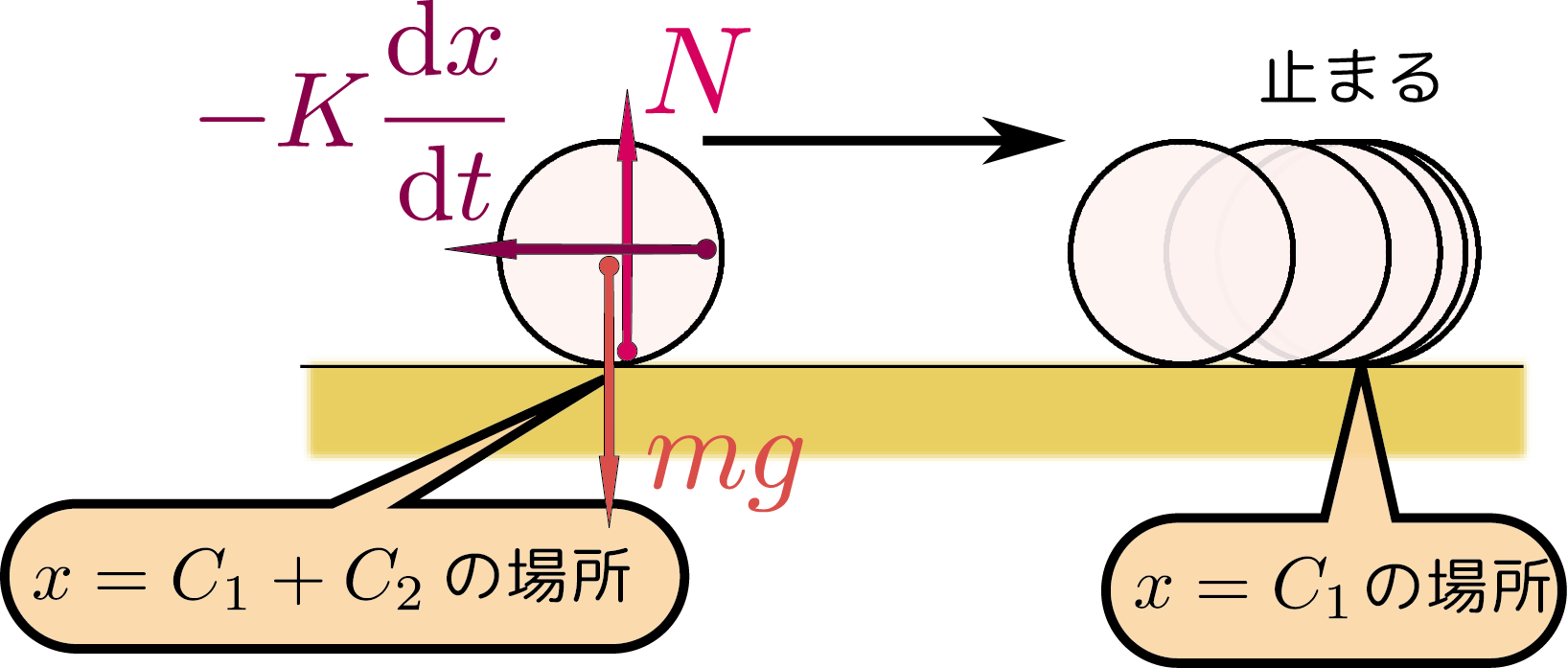
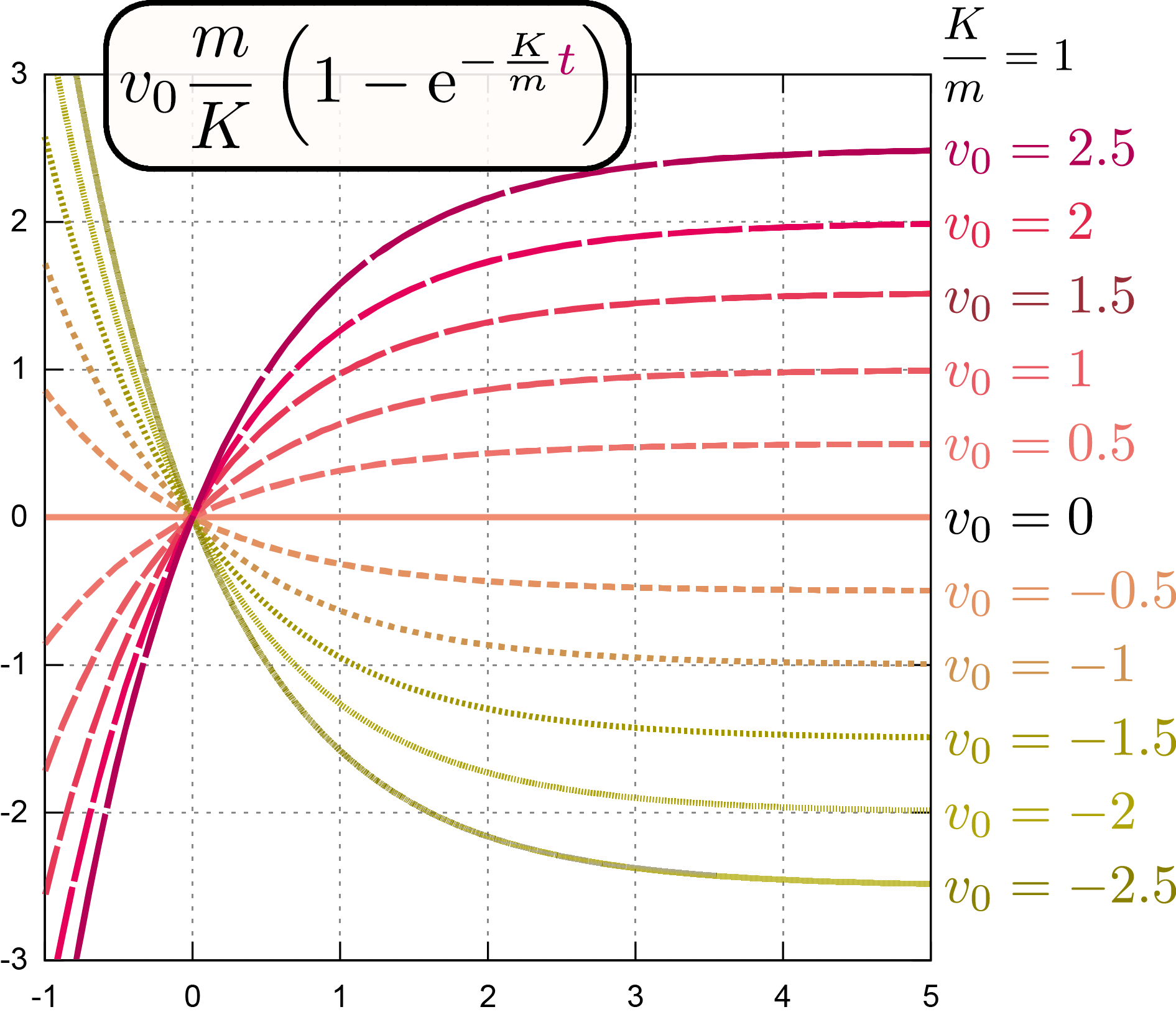
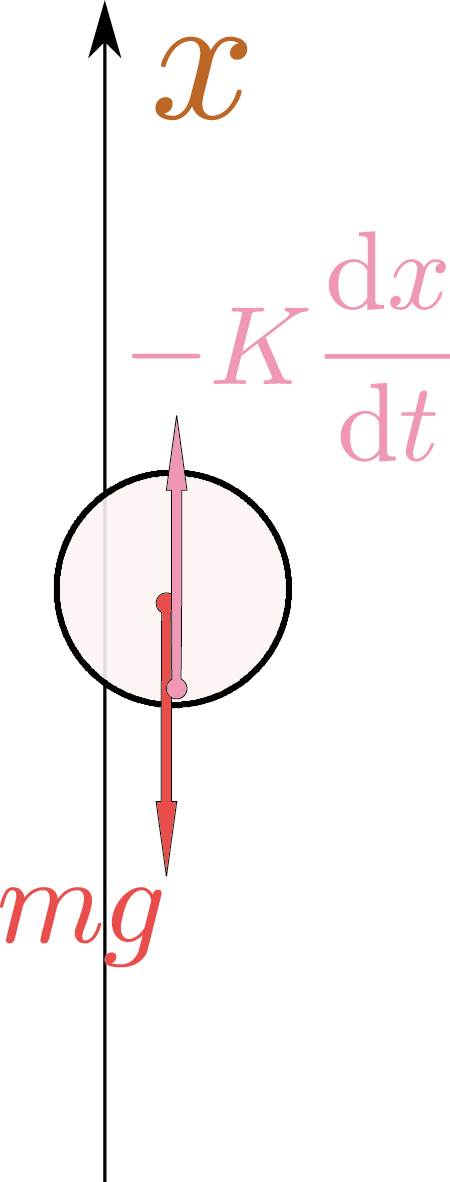
$\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{{↓#1}}\def\goverbrace{\overbrace}$
前回で、定数係数の線形微分方程式の解き方として二階線形の定数係数微分方程式を例として
$$
\left(a\left(\ddx\right)^2+b\ddx +c\right)\ycol{y}=0
$$
の解として$y=\E^{\lambda\xcol{x}}$を仮定し、$\E^{\lambda\xcol{x}}$の前では$\ddx$が$\lambda$に置き換えられること($\ddx\E^{\lambda\xcol{x}}=\lambda\E^{\lambda\xcol{x}}$)を用いて
$$
\left(a\lambda^2+b\lambda +c\right)\ycol{y}=0
$$
として特性方程式
$$
a\lambda^2+b\lambda +c=0
$$
を解き、その解が$\lambda_1,\lambda_2$と二つ求められたとすれば、
$$
\ycol{y}=\alpha \E^{\lambda_1\xcol{x}}+\beta\E^{\lambda_2\xcol{x}}
$$
が解である。
という解き方を学んだ。ここで前回の宿題として残っていたのは、特性方程式$a\lambda^2+b\lambda +c=0$が重解もしくは複素数解を持っていた場合である。
特性方程式が重解を持つ場合
特性方程式が重解になる微分方程式
\begin{equation}
\left(
\left(\ddx\right)^2 -2A\ddx +A^2
\right)f\kakko{\xcol{x}}=0~~~すなわち~~~
\left(
\ddx - A
\right)^2 f\kakko{\xcol{x}}=0
\end{equation}
を見て、$\left(\ddx - A\right) f\kakko{\xcol{x}}=0$になる関数を求めればよいと考えると、$f\kakko{\xcol{x}}=C\E^{A\xcol{x}}$という解はすぐに出る。しかしこれで終わりではない。そもそも二階微分方程式を解いているのだから、解は二つの未定パラメータを含まなくてはならない。つまり線形独立な解がもう1個出る。ではもう一つの解はどうなるのだろう?
さて、我々が求めたいのは「$\left(\ddx - A\right)$を二回掛けると0になる関数」つまり、
\begin{equation}
\left(\ddx - A\right)\left(\ddx - A\right)f\kakko{\xcol{x}} =0
\end{equation}
を満たす$f\kakko{\xcol{x}}$である。$f\kakko{\xcol{x}}=C\E^{A\xcol{x}}$が上の式を満たすのはもちろんだが、これだけでは解が足りない。$\left(\ddx - A\right)f\kakko{\xcol{x}}=\E^{A\xcol{x}}$}を満たす関数$f\kakko{\xcol{x}}$があれば、
\begin{equation}
\left(\ddx - A\right)\underbrace{\left(\ddx - A\right)f\kakko{\xcol{x}}}_{\E^{A\xcol{x}}}
=\left(\ddx - A\right){\E^{A\xcol{x}}}=0
\end{equation}
となるので、それも解となる。そうなる関数はすぐに見つかり、$\xcol{x}\E^{A\xcol{x}}$である。確認しよう。
\begin{equation}
\left(\ddx - A\right)\left(
\xcol{x}\E^{A\xcol{x}}
\right)=\ddx\left(\xcol{x}\E^{A\xcol{x}}
\right)-A\xcol{x}\E^{A\xcol{x}}
=\E^{A\xcol{x}}+\underbrace{
A\xcol{x}\E^{A\xcol{x}}-A\xcol{x}\E^{A\xcol{x}}
}_{相殺}\label{xexpx}
\end{equation}
こうして、重解である場合はもう一つの解$D\xcol{x}\E^{A\xcol{x}}$が出ることがわかったので、
二階線形微分方程式の特性方程式が重解を持つ場合の解
\begin{equation}
\left(\ddx - A\right)^2 f\kakko{\xcol{x}}=0~~~の解は~~~
f\kakko{\xcol{x}}=\left(D\xcol{x}+C\right)\E^{A\xcol{x}}
\end{equation}
がわかる。これで未定パラメータを2個含む解になった。
この答えを出す方法として、
\begin{equation}
任意の関数g\kakko{\xcol{x}}に対し、~~
\left(\ddx-A\right)\left(
\E^{A\xcol{x}}g\kakko{\xcol{x}}\right)
= \E^{A\xcol{x}}\ddx g\kakko{\xcol{x}}\label{ddxA}
\end{equation}
を先に証明しておくのも良い方法である(後で応用が効く)。すなわち、以下の置き換えができる。
$\ddx-A$という微分演算子の後にあった$\E^{A\xcol{x}}$という数を微分演算子より前に出すと、
\begin{equation}
\left(\ddx-A\right)\left(
\E^{A\xcol{x}}\fbox{なんとか}\right)
\to \E^{A\xcol{x}}\ddx\fbox{なんとか}\label{okikaeeax}
\end{equation}
のように$\ddx-A$の$-A$が消えて$\ddx$になる。
この置き換えを使うと、$\left(\ddx - A\right)^2 \left(\E^{A\xcol{x}}g\kakko{\xcol{x}}\right)=0$という方程式は$\E^{A\xcol{x}}\left(\ddx\right)^2 g\kakko{\xcol{x}}=0$という方程式に変わるから、解き易い後者の式を解けばよい(この答えが$g\kakko{\xcol{x}}=D\xcol{x}+C$であることはもう知っている)。
微分の階数が高くなったら多項式の次数をそれに応じて上げて
\begin{equation}
\left(
\ddx - A
\right)^k f\kakko{\xcol{x}}=0~~~の解は~~~
\left(
C_{k-1}\xcol{x}^{k-1}+
C_{k-2}\xcol{x}^{k-2}+
\cdots+C_1\xcol{x}+C_0\right)\E^{A\xcol{x}}
\end{equation}
とすればよい。
以上の結果をまとめておこう。定数係数の線形同次微分方程式
$$
\left(
A_n\left(\ddx\right)^n
+A_{n-1}\left(\ddx\right)^{n-1}
+\cdots
+A_{1}{\ddx}
+A_0
\right)\ycol{y} =0
$$
を解くには、微分演算子$\left(\ddx\right)^n$を$\lambda^n$という数に置き換えて、
$$
A_n\lambda^n
+A_{n-1}\lambda^{n-1}
+\cdots
+A_{1}\lambda
+A_0
=0
$$
という特性方程式を作る。この方程式が$n$個の相異なる解$\lambda_1,\lambda_2,\cdots,\lambda_n$を持っていたならば、
\begin{equation}
C_1\E^{\lambda_1\xcol{x}}
+ C_2\E^{\lambda_2\xcol{x}}
+ C_3\E^{\lambda_3\xcol{x}}
+\cdots
+ C_n\E^{\lambda_n\xcol{x}}
\end{equation}
が解である。解が$m$重解を含んでいた場合、重解である$\lambda_k$に対しては上の式の$C_k\E^{\lambda_k\xcol{x}}$を
\begin{equation}
\left(
C_{k,m-1}\xcol{x}^{m-1}
+C_{k,m-2}\xcol{x}^{m-2}
+\cdots
+C_{k,1}\xcol{x}
+C_{k,0}
\right)\E^{\lambda_k\xcol{x}}
\end{equation}
と置き換える(上は$m$重解の場合で、$m$個のパラメータを含む)。
残るは$\lambda$が複素数解を持つ場合だが、その点については次の節で考えよう。
複素数を使って解く
ここでは、複素数を使うことで微分方程式がどのように解きやすくなるのかを解説しよう。
複素数の微分方程式での利用例として、非常によく出てくる以下の方程式を考えよう(これはたとえば振り子の運動方程式である)。
\begin{equation}
\left( \ddx \right)^2\ycol{y}= -\ycol{y}\label{tansindounosiki}
\end{equation}
ここまでやってきた定数係数の線形微分方程式の一般論からすると、$\ycol{y}={\E^{\lambda \xcol{x}}}$としたくなるところだが、代入すると
\begin{equation}
\lambda^2\goverbrace{\E^{\lambda \xcol{x}}}^{\ycol{y}}= -\goverbrace{\E^{\lambda \xcol{x}}}^{\ycol{y}}
\end{equation}
となり、$\lambda^2=-1$という「実数の範囲で考えれば解なし」の方程式が出てくる。虚数を知らない人は、ここで「ああ、この微分方程式はこの方法では解けない」と諦めてしまう。しかしすでに虚数を知っている我々は、$\lambda=\pm\I$という「とりあえずの答え」を出して、「$\left(\ddx\right)^2\ycol{y}= -\ycol{y}$の解は、$\E^{\I \xcol{x}}$と$\E^{-\I \xcol{x}}$(およびその線形結合)である」と考えて先に進む。
答えが実数じゃなくていいんですか?
「とりあえずの答え」ならよい。実数ではなくてはならないのは最終的に求められる解であって、計算の途中で現れる量は複素数でもよい。最終結果が実数であるように、以下で調節する。
先に進んでみよう。一般解は
\begin{equation}
\ycol{y}=A\E^{\I \xcol{x}}+ B\E^{-\I \xcol{x}}\label{Csindou}
\end{equation}
となる。$A$と$B$は今から選ぶ定数(複素数であってよい)である。
この答えは一見複素数に見えるが、実際に欲しいのは実数解である。そこで、以下の二つの考え方のどちらかで実数解を得る。
- この解が実数になるように任意パラメータの$A,B$を調整する。
- この解のうち実数部分を取り出せばそれが欲しい解である。
(1)の方法で考えよう。この解が実数になれということは、複素共役である
\begin{equation}
\ycol{y}^*=
A^* \E^{-\I \xcol{x}}
+B^* \E^{\I \xcol{x}}\label{Csindoustar}
\end{equation}
が元の$\ycol{y}$と同じであれ、ということである。そうなるためには、$A^*=B$であればよい。こうすると自動的に$B^*=A$であることになる。こうして$A$と$B$に関係がついたから、以後は$B$を$A^*$と書くことにして、
\begin{equation}
\ycol{y}=A \E^{\I \xcol{x}}
+A^* \E^{-\I \xcol{x}}
\end{equation}
を解とすればよい。ここで、複素数である$A$を極表示して$A=|A|\E^{\I\alpha}$($\alpha$は実数)とすると、
\begin{equation}
\ycol{y}=
|A|\left(
\E^{\I(\xcol{x}+\alpha)}
+\E^{-\I(\xcol{x}+\alpha)}\right)
\end{equation}
と答えをまとめることができる(この形の方が実数であることが明白である)。
さらに${\E^{\I\theta}+\E^{-\I\theta}\over 2}=\cos\theta$を使うと、以下のようにまとまる。
\begin{equation}
\ycol{y}=2|A|\cos\kakko{\xcol{x}+\alpha}
\end{equation}
となって、よくみた振り子などの単振動の式の形にまとまる。