弱肉強食の微分方程式

$\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}$

兎と狐の増減

　ある森の中で草食動物（兎）の数$\rcol{X}$と肉食動物（狐）の数$\thetacol{Y}$がどう増減するかを考える（簡単のため、この森にはこの2種類の動物しかいないものとする）。

　餌が豊富にあり、かつ狐がいないと考えた場合、兎は今いる量に比例して増えると同時に寿命が来て死ぬ分減る（減る量も今いる量に比例する）。この二つの効果のみを考えるならば、 \begin{equation} \opcol{\diff\rcol{X}\over \kidt}= A\rcol{X}\label{lwonezero} \end{equation} という微分方程式で兎の数$\rcol{X}$の変化が記述できそうである。ただし$A$は比例定数で兎は自然には増えるということを反映して、正の定数となる。

　ところが兎が減る原因はもう一つある。狐は兎を食べるので、兎は狐と出会うと死ぬと考えよう。森の中に$\rcol{X}$匹の兎と$\thetacol{Y}$匹の狐がそれぞれ動きまわっている状況を考えると、両者が出会う確率は$\rcol{X}$と$\thetacol{Y}$の積に比例するだろう。そして出会った後でやはりある確率で「狐が兎を食べる」というイベントが発生し、兎が減る。このように考えると、兎の減少量として$\rcol{X}\thetacol{Y}$という積に比例する部分が出てくる。よって、兎の数は \begin{equation} \opcol{\diff\rcol{X}\over \kidt}= A\rcol{X} -B\rcol{X}\thetacol{Y}\label{lwone} \end{equation} という式で増減するとする（$B$は$A$とは別の比例定数）。

　一方狐は、兎を食べないと生きていけないのだから、その増加はどれだけ兎を食べられるかによって決まり、それは$\rcol{X}\thetacol{Y}$に比例するのだったから、狐は$\rcol{X}\thetacol{Y}$に比例して増える。兎がいなかったら狐は「繁殖しつつ寿命が来て死ぬ」という現象の結果として現在いる量に比例して減っていくだろう。それを$-C\thetacol{Y}$という形（$C$は正の定数、ほっておくと増える兎とは符号が逆になる）で式の右辺に入れて、 \begin{equation} \opcol{\diff\thetacol{Y}\over \kidt}= -C \thetacol{Y} + D \rcol{X}\thetacol{Y}\label{lwtwo} \end{equation} という微分方程式に従う（$C,D$は$A,B$とは別の比例定数である）。これらの方程式はこの式を出した二人の数学者の名前を取って「ロトカ・ヴォルテラの方程式」と呼ばれる。

　時間変化を考えるには、$\opcol{\diff \rcol{X}\over \kidt},\opcol{\diff\thetacol{Y}\over \kidt}$に関する二つの微分方程式を連立させて解けばよい。

　いきなり解けと言われても、どうしていいのか悩んでしまうかもしれない（この式は非線形だし）。そこでまず、「$\opcol{\diff \rcol{X}\over \kidt}=\opcol{\diff\thetacol{Y}\over \kidt}=0$となるのはどんなときか？」から考える。$\opcol{\diff \rcol{X}\over \kidt}=\opcol{\diff\thetacol{Y}\over \kidt}=0$となる点を「固定点」と呼ぶ。

　固定点を求める方程式は上の微分方程式の右辺が$0$になる、という式で、因数分解すれば \begin{eqnarray} \rcol{X}(A-B\thetacol{Y})&=&0\\ \thetacol{Y}(-C+D\rcol{X})&=&0 \end{eqnarray} である。$\rcol{X}=\thetacol{Y}=0$もこの方程式の解だが、「兎も狐もいない」という「つまらない解」最初から兎も狐もいないのだから、未来永劫いないままである。なので無視する。

　$\rcol{X}={C\over D},\thetacol{Y}={A\over B}$が意味のある固定点である。

　固定点からずれた時の$\opcol{\diff\rcol{X}\over\kidt},\opcol{\diff \thetacol{Y}\over\kidt}$の様子をグラフに表示すると次のグラフのようになる。

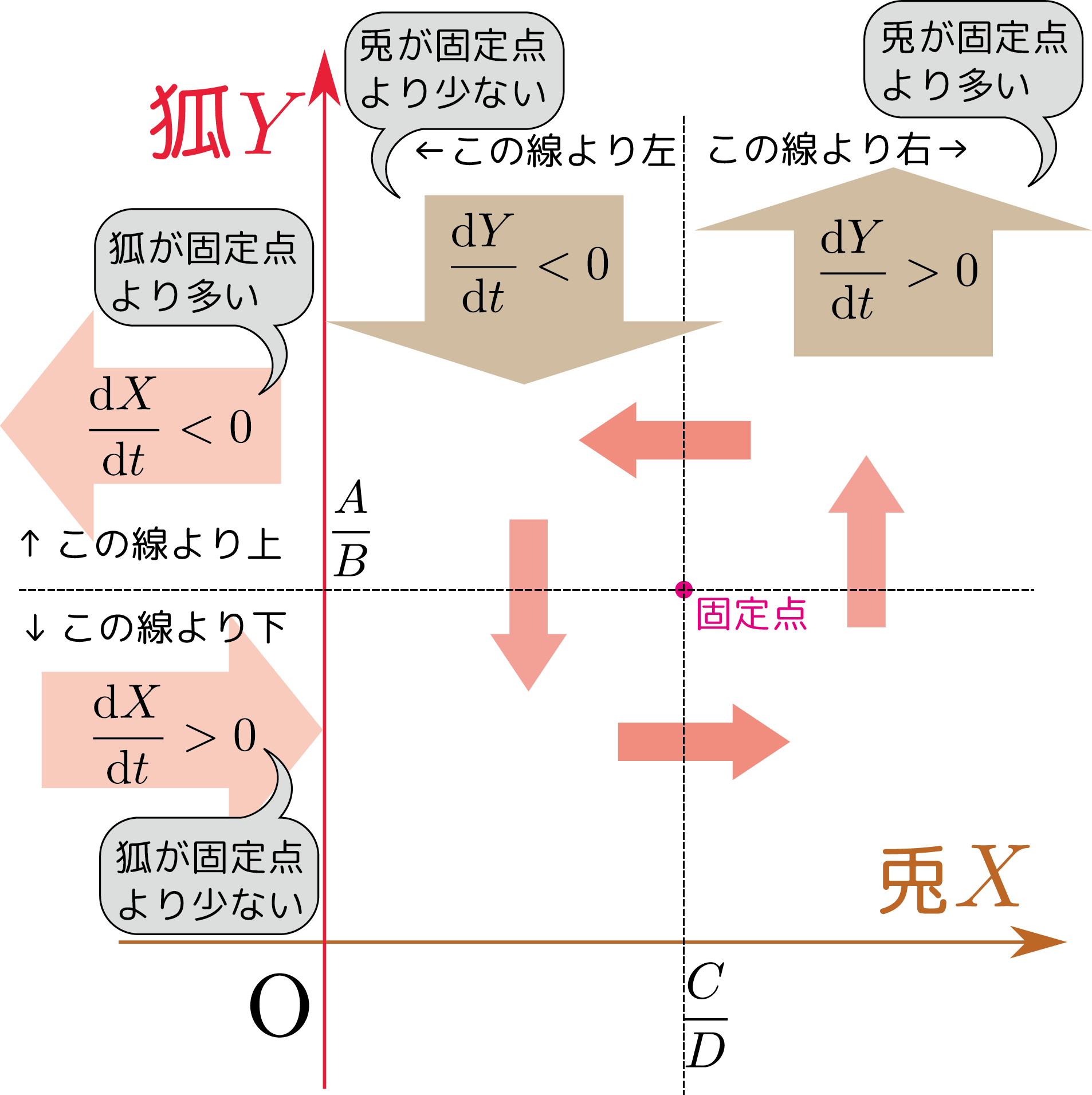
これから$\rcol{X}$-$\thetacol{Y}$平面内で反時計周りにぐるぐる回るような時間発展を行うということが予想される。

　固定点からのずれを$\xcol{x},\ycol{y}$とする。つまり、 \begin{equation} \rcol{X}= {C\over D}+\xcol{x},~~\thetacol{Y}={A\over B}+\ycol{y} \end{equation} とする。こうして$\xcol{x},\ycol{y}$の微分方程式を作ると、 \begin{equation} {\coldx\over \coldt}= -B \left({C\over D}+\xcol{x}\right) \ycol{y},~~~ {\coldy \over \coldt}= D\left({A\over B}+\ycol{y}\right)\xcol{x} \end{equation} となる。ここで$\xcol{x},\ycol{y}$は${C\over D},{A\over B}$に比べて小さいと考えて、括弧内の$\xcol{x},\ycol{y}$は無視して、 \begin{equation} {\coldx\over \coldt}= -{BC\over D} \ycol{y},~~~ {\coldy \over \coldt}= {AD\over B} \xcol{x} \end{equation} と近似する。第一式を微分して \begin{equation} {\coldtwox\over \coldt^2}= -{BC\over D} {\coldy\over \coldt} \end{equation} にしてから第二式を代入すると \begin{equation} {\coldtwox\over \coldt^2}= -{BC\over D}\times{AD\over B}\xcol{x}=-{AC}\xcol{x} \end{equation} という、係数は違うが単振動と同じ式が出てくる。解はすでに知っていて、 \begin{equation} x\kakko{\tcol{t}}=x_0 \cos\kakko{\sqrt{AC}\tcol{t}+\alpha} \end{equation} と書ける。

授業ではこの↑解が質問してもすぐに出てこなくてびっくりした。これぐらいはささっと出てくるようでないと勉強が足りない。これを覚えるべきということではなく、普通に勉強していれば何度でもこの式が出てきて覚えてしまっているはず、ということ。

　$\cos$の中の$\tcol{t}$の前に$\sqrt{AC}$がついているのは、この微分方程式が「二階微分すると元の$-AC$倍になる」という式だからである。$x_0,\alpha$は微分方程式からは決まらないパラメータである（二階微分方程式だからこれでちょうどよい）。

　${\coldx\over \coldt}=-{BC\over D} \ycol{y}$なので、$\sqrt{AC}=\omega$として \begin{equation} \begin{array}{rl} -\omega x_0 \sin\kakko{\omega \tcol{t}+\alpha}= &-{BC\over D} y\kakko{\tcol{t}} \\ {D\over BC}\times\omega x_0 \sin\kakko{\omega \tcol{t}+\alpha}= &y\kakko{\tcol{t}} \end{array} \end{equation} で$\ycol{y}$も求まる。

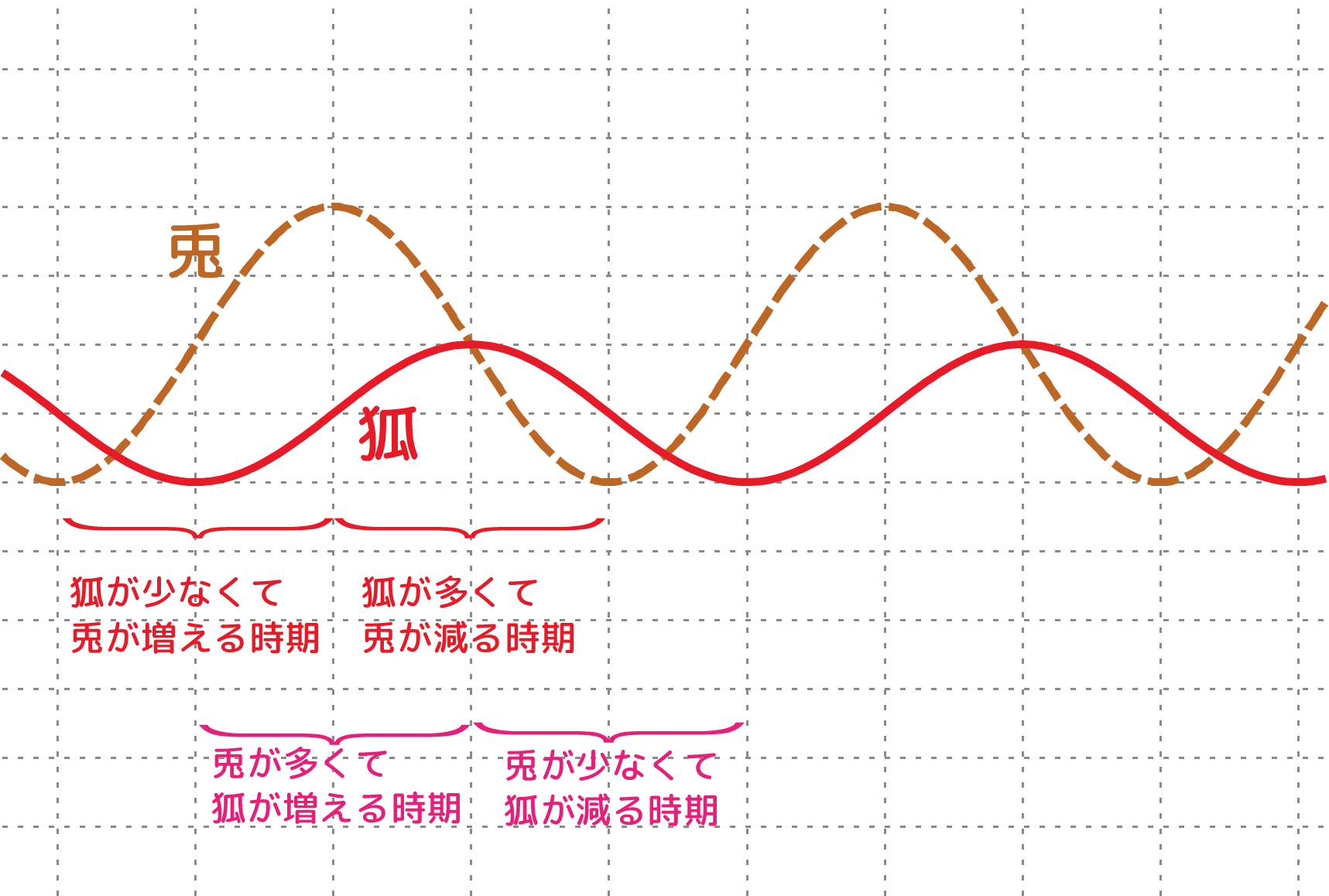
　$\rcol{X},\thetacol{Y}$の時間変化を表すのが左のグラフである。$\xcol{x},\ycol{y}$と$\rcol{X},\thetacol{Y}$は定数を足しただけの違いなので、$\rcol{X}$（兎）の変化は$\cos$で、$\thetacol{Y}$（狐）の変化は$\sin$で表されていると思えばよい。

　グラフに示したように、狐のグラフが「山」である間は兎のグラフは右下がり、狐のグラフが「谷」である間は兎のグラフが右上がりとなる。もちろんこれは「狐が多くて兎が食われる時期は兎が減り、狐が少なくなると兎が増える」を示している。逆に「兎が多いと狐が増える（およびこの逆）」もわかる。グラフを見ながらそれを確認してみよう。

　ここで、時間変化が周期的になること、つまりある程度の時間がたつと（正確に言えば$\tcol{t}$が${2\pi\over \sqrt{AC}}$だけ増加すると）$\rcol{X}$と$\thetacol{Y}$は元の値に戻るということに注意しよう。

　ここまでで求めたのは近似解なので、$\rcol{X}$-$\thetacol{Y}$平面に描かれる図形は単純な楕円であるが、実際に微分方程式を解いてみると少々複雑な図形を描く（次のグラフではコンピュータで数値的に計算させた）。

　動くグラフはにある。

　グラフでは$A=B=C=D=1$にして、$\rcol{X},\thetacol{Y}$の初期値を変えてグラフにしている。この場合は$(\rcol{X},\thetacol{Y})=(1,1)$が固定点であり、その周りをめぐる軌跡を描く。固定点からの外れが小さい領域では軌跡は円に近い（円なのは今の場合は${D\over BC}=1$だから）。

多変数関数

多変数関数と自由度

1変数の場合の「関数」とは、「独立変数ある量$A$を決めると、従属変数ある量$B$が決まる」という対応関係であった。 独立変数が一つの量ではなくなり、

という対応関係もちろん、ある量$B$はただひとつに定まらなくてはいけない。となったものを「多変数関数」と呼ぶこの「多」は「独立変数が複数」という意味である。。$\xcol{x},\ycol{y}$を決めると$\zcol{z}$が決まる、という対応関係（この場合は「2変数関数」である）なら、$\zcol{z}=f\kakko{\xcol{x},\ycol{y}}$のように書く。たとえば$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}\ycol{y},f\kakko{\xcol{x},\ycol{y}}=\xcol{x}+\ycol{y},f\kakko{\xcol{x},\ycol{y}}=\E^{\xcol{x}}\cos \ycol{y},\cdots$など、いろいろな場合がある。

　現実的な問題では複数（2どころか3や4やもっと多く）の独立変数を持っていて、複雑な関数になっている場合がほとんどだ。だから、多変数関数を自由に使えるようになってこそ、「使える数学」になる。

　以下で簡単な2変数関数の例を挙げよう。

例1：長方形の面積 $\rcol{S}=\xcol{x}\ycol{y}$

　横$\xcol{x}$、縦$\ycol{y}$の長方形の面積$\rcol{S}$は$\rcol{S}=\xcol{x}\ycol{y}$であり、$\xcol{x}$と$\ycol{y}$の両方を決めないと決まらない。つまり長方形の面積は2変数関数である。関数として表現すれば$S\kakko{\xcol{x},\ycol{y}}=\xcol{x}\ycol{y}$となる。

例2：平面上の距離 $\rcol{R}=\sqrt{\xcol{x}^2+\ycol{y}^2}$

　原点から点$(\xcol{x},\ycol{y})$までの距離は$R\kakko{\xcol{x},\ycol{y}}=\sqrt{\xcol{x}^2+\ycol{y}^2}$という2変数関数で計算される。

例3：円柱の体積 $\thetacol{V}=\pi\rcol{r}^2\xcol{h}$

　底面が半径$\rcol{r}$の円で高さが$\xcol{h}$の円柱の体積は$V\kakko{\rcol{r},\xcol{h}}=\pi \rcol{r}^2\xcol{h} $となる。

　さらに複雑なものをいくらでも考えることができるだろう。たとえば直方体の体積は$\rcol{V}=\xcol{x}\ycol{y}\zcol{z}$のような3変数関数である。

　1変数の関数は、独立変数と従属変数という二つの変数を持っているが、独立変数一つを決めれば従属変数も決まったから「自由に動かせる数」は一つであった。

　この「自由に動かせる数が一つ」ということを 「自由度が1だ」と表現する。2変数の関数の場合、二つの独立変数を決めると従属変数が決まるから、自由度は2である（3変数、4変数と増えていっても同じである）。

　1変数の関数は$\xcol{x}$-$\ycol{y}$という平面の上に描かれた「線（一般には曲線）」で表現された。線は「自由度1」あるいは「1次元」の存在である（つまり、線の上の点は1方向にのみ動ける）。同様に2変数の関数は「面（一般には曲面）」で表現されるそもそも「次元」というのは「自由に動ける方向の数」を意味する（1次元なら線、2次元なら面、3次元なら立体）。。

次に、$f\kakko{\xcol{x},\ycol{y}}=\E^{\xcol{x}}\cos\ycol{y}$という2変数関数の「立体グラフ」を示そう。

　非常に単純な2変数関数$\zcol{z}=f\kakko{\xcol{x},\ycol{y}}=a\xcol{x}+b\ycol{y}+c$を考えると、これは$(\xcol{x},\ycol{y},\zcol{z})$という3次元空間の中にある（傾いた）平面を表現している。原点$(\xcol{x},\ycol{y})=(0,0)$に置いては$\zcol{z}=c$で、$\xcol{x}$方向に移動すると移動量$\times a$だけ$\zcol{z}$が増え、$\ycol{y}$方向に移動すると移動量$\times b$だけ$\zcol{z}$が増える。増加量が移動量$\times$（一定値）になっているので、この図形は平面になる。

　今日はまず、下の図（実際に授業で使ったのはandroidアプリのバージョン）で2変数関数のイメージを持ってもらった。

　この図を動かしながら、この式の１次の係数（xの前の係数とyの前の係数）が「面の傾き」を表現していることを確認して欲しい。

この場合「傾き」はx方向の傾きとy方向の傾きの二つがあること（1変数の関数のときは「傾き」と言えば一つに決まったが、そうはいかないこと）に注意しておいて欲しい。

多変数の微分

　1変数のときの微分または微係数とは、「たとえ複雑に見える関数のグラフでも非常に狭い範囲のみを考えれば直線と近似できる（あるいは、どんな関数のグラフも拡大していけば直線のグラフになる）これは微分可能な関数に限った話である。から、その直線の傾きを求める」というのがその定義であった。2変数の場合の「グラフ」は線ではなく面になるが、この面も（微分可能な関数なら）局所的な狭い範囲に注目すれば（別の考え方では「拡大していけば」）平面になる。その平面の傾きに対応するものが2変数関数の「微分」であるが、「接線」の場合と違って「接平面」の傾きは一つの数字では表現できない。

　前節であげた三つの例のうち二つ（距離については来週やる）について、「微分」を考えよう。

例1：$\rcol{S}=\xcol{x}\ycol{y}$

　長方形の面積$\rcol{S}=\xcol{x}\ycol{y}$について、二つの変数$\xcol{x}$と$\ycol{y}$を変化させるとどうなるかを考えてみよう。この二つの変数は次の図のように、別々に（独立に）変化させることができる。

　上の図から「$\xcol{x}$が$\coldx$変化したときには$\rcol{S}$が$\ycol{y}\coldx$だけ変化する」と「$\ycol{y}$が$\coldy$変化したときには$\rcol{S}$が$\xcol{x}\coldy$だけ変化する」の二つがわかるから、 \begin{equation} \rcol{\mathrm dS}=\ycol{y}\coldx+ \xcol{x}\coldy \end{equation} という式が成立することがわかる。これは$\rcol{S}=\xcol{x}\ycol{y}$をライプニッツ則にしたがって \begin{equation} \rcol{\mathrm dS}=\underbrace{\coldx \ycol{y}}_{\xcol{x}を微分した項}+ \underbrace{\xcol{x}\coldy}_{\ycol{y}を微分した項} \end{equation} と微分したと考えても同じことであるし、 \begin{equation} \left(\xcol{x}+\coldx\right) \left(\ycol{y}+\coldy\right)-\xcol{x}\ycol{y}=\ycol{y}\coldx+ \xcol{x}\coldy+\underbrace{\coldx\coldy}_{高次の微小量} \end{equation} のように「変化後$-$変化前」という引算をおこなって高次の微小量を無視することでも求めることができる。

例3：円柱の体積

　高さ$\xcol{h}$を$\xcol{\mathrm dh}$変化させたとすると、その変化による体積の変化は$\pi\rcol{r}^2 \xcol{\mathrm dh}$である。半径が$\rcol{\mathrm dr}$変化する場合の体積変化は$2\pi \rcol{r}\xcol{h}\rcol{\mathrm dr}$となる。

　この二つの量（$\pi\rcol{r}^2 \xcol{\mathrm dh}$と$2\pi \rcol{r}\xcol{h}\rcol{\mathrm dr}$）は、上の図に示した体積増加部分であるが、微分を使って数式で表現すれば、 \begin{equation} \mathrm dV\kakko{\rcol{r},\xcol{h}} = \pi \rcol{r}^2\xcol{\mathrm dh} + 2\pi\rcol{r}\xcol{h}\rcol{\mathrm dr} \end{equation} となる。二つの係数がそれぞれ底面積（図では「天井の面積」として描いているが）と側面積という意味を持っていることに注意しよう。

　こうして、2変数関数では二つの変化を考える必要があることがわかったが、その微分（偏微分）の計算と新しい数式の定義については次回。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

タブレットの画面はこんな感じです↓