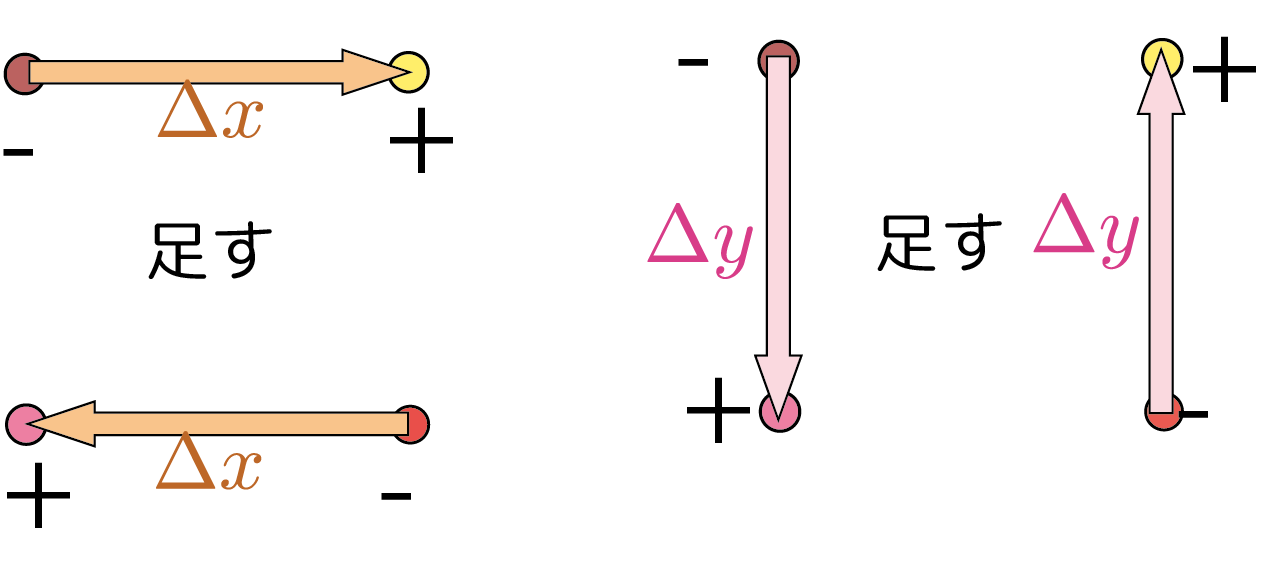偏微分と極大・極小

$\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}$

多変数関数のグラフ

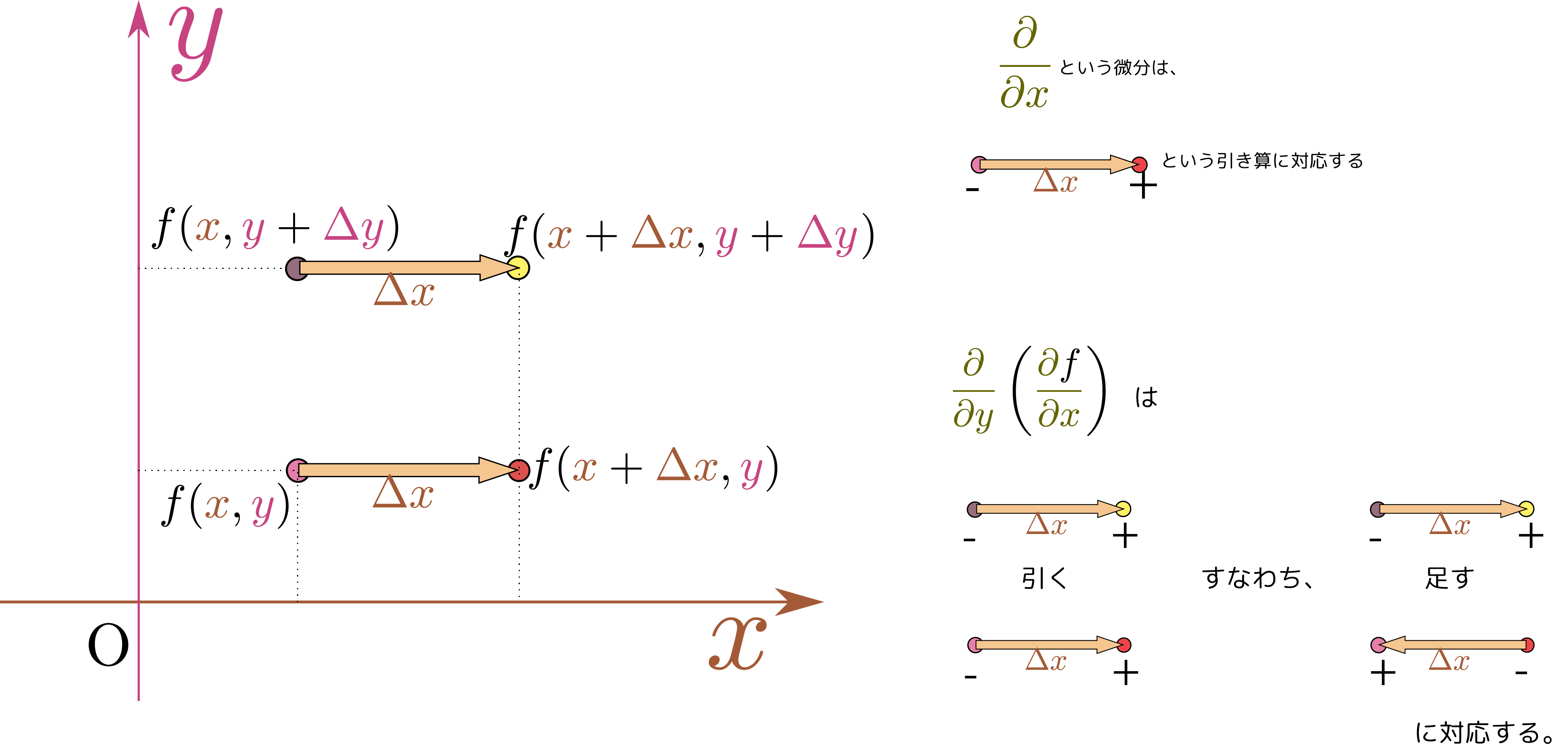
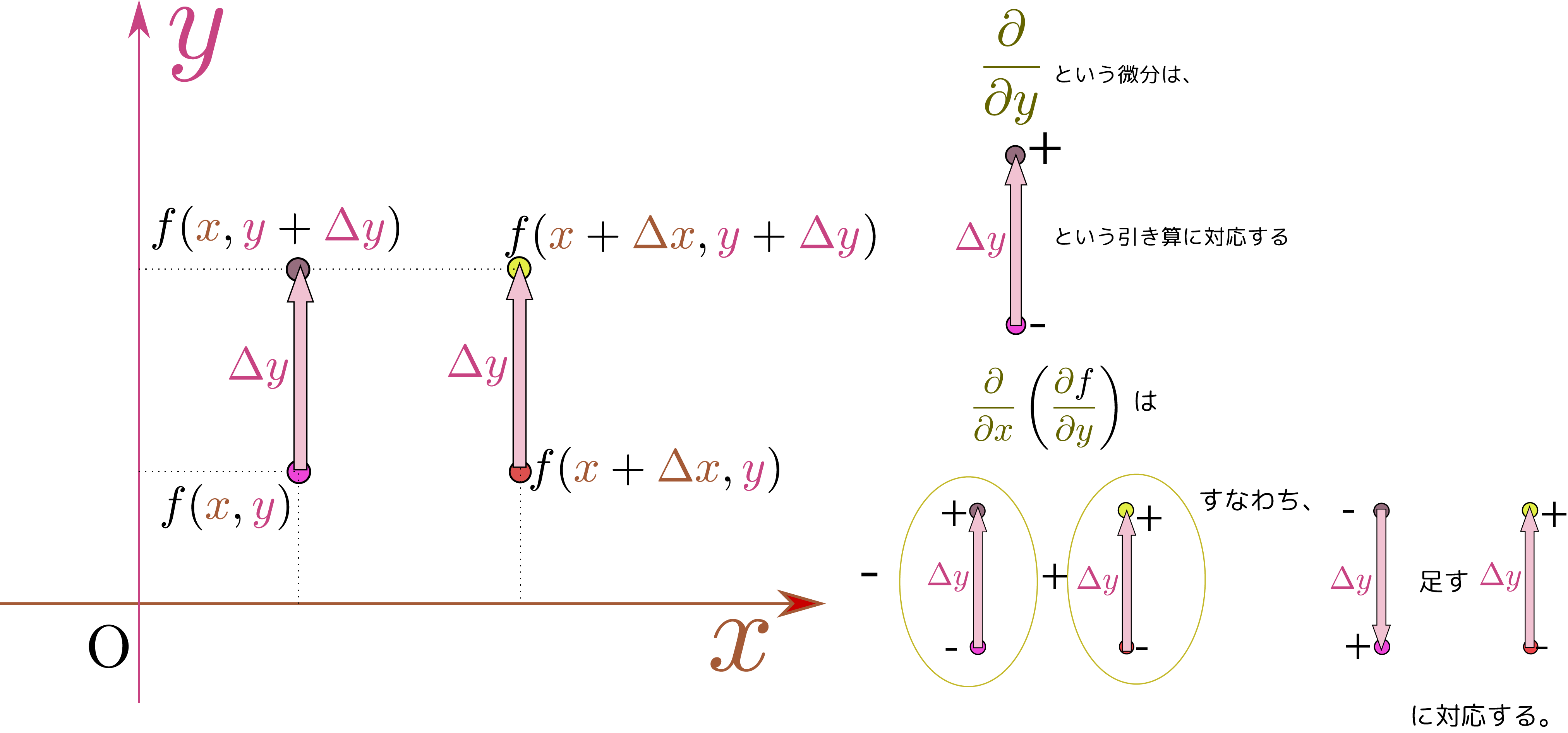
　先週は簡単な例で2変数関数の極大・極小を考えた。その例では、$\PPD{f}{\xcol{x}}$と$\PPD{f}{\ycol{y}}$の正負を見て場合分けできたが、2変数関数の二階微分はもう一つ、$\PPDD{f}{\xcol{x}}{\ycol{y}}$もある（これまでの例では全て$\opcol{{\partial^2 \kuro{f}\over \partial \xcol{x}\partial \ycol{y}}}=0$なので気にしなくてもよかった）。

　逆に$\PPDD{f}{\xcol{x}}{\ycol{y}}\neq0$である例として、$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}\ycol{y}$の原点$(0,0)$を考えてみると、この場所も鞍点になっている実はこのグラフは$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}^2-\ycol{y}^2$を${\pi\over 4}$だけ回転して、少し高さを調整したものになっている。。

↓のような曲面を作るため、ストッキングを持っていって曲げたり伸ばしたりしながら授業した。

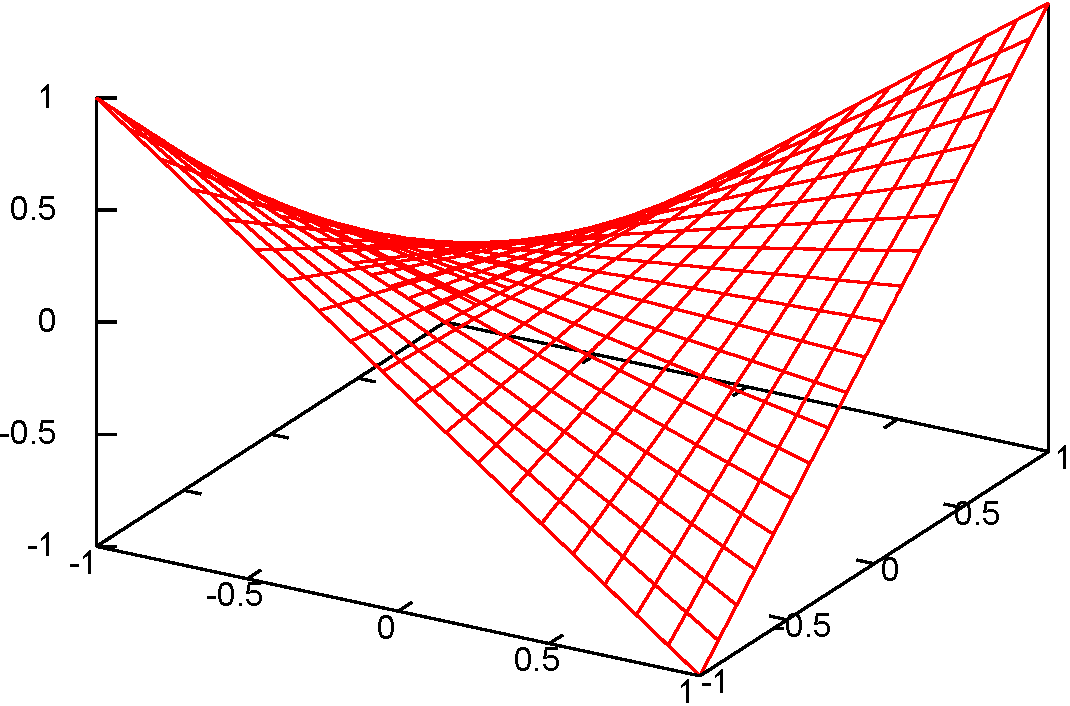
　一般の2変数関数で、一階微分が全て0である点（このような点は「停留点」と呼ぶ停留点の中には、極大点と極小点と鞍点が含まれる。）が見つかったとして、その点が極大なのか極小なのかそれとも鞍点なのかを知りたい「別にそんなの知りたくない」って？---この関数がたとえば貴方の所有している財産の価値だったら、「ここが極大かどうか」を知りたくならないかな？場合は、テイラー展開の2次の項を調べる必要がある。

　$(a,b)$が停留点とすればそこで一階微分は0だから、$(\xcol{x}-a)=\xcol{\Delta x},(\ycol{y}-b)=\ycol{\Delta y}$と書けば、 \begin{equation} f\kakko{\xcol{x},\ycol{y}} =f\kakko{a,b} +\goverbrace{\underbrace{{1\over 2}\PPD{f}{\xcol{x}}}_a(\xcol{\Delta x})^2 +\underbrace{\PPDD{f}{\xcol{x}}{\ycol{y}}}_b\xcol{\Delta x}\ycol{\Delta y} +\underbrace{{1\over 2}\PPD{f}{\ycol{y}}}_c(\ycol{\Delta y})^2}^{曲がり具合を表現する部分} +\cdots \end{equation} となる。3次以上の項$(\cdots)$は省略した。式に示したように、係数を以下$a,b,c$で表す。

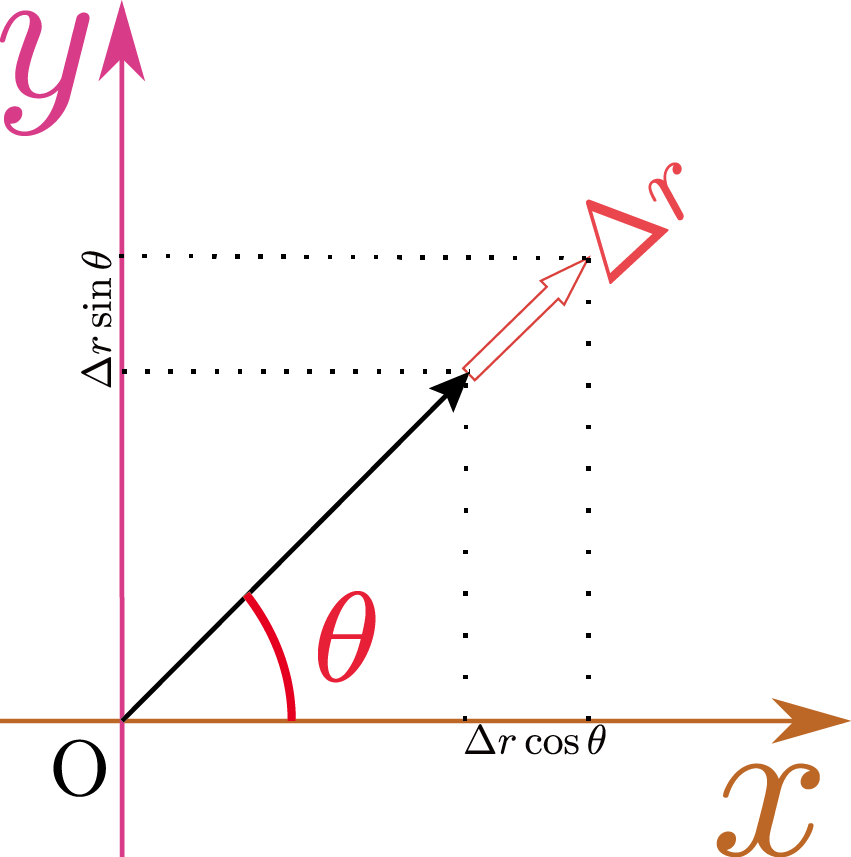
　上の「曲がり具合を表現する部分」がどのような$\xcol{\Delta x},\ycol{\Delta y}$に対しても正であるならばこの点は極小点、逆に常に負ならば極大点である。正にも負にもなる場合は鞍点だと言える（他の可能性としては正、負ではなく0以上や0以下という可能性もある）。この式は \begin{equation} a(\xcol{\Delta x})^2 + b\xcol{\Delta x}\ycol{\Delta y}+c(\ycol{\Delta y})^2 =\underbrace{(\ycol{\Delta y})^2}_{常に正}\underbrace{ \left( a\left({\xcol{\Delta x}\over\ycol{\Delta y} }\right)^2 +b{\xcol{\Delta x}\over\ycol{\Delta y} }+c \right)}_{この部分の正負が問題} \end{equation} となるから、$\tcol{t}={\xcol{\Delta x}\over\ycol{\Delta y}}$とすれば後は「二次式$a\tcol{t}^2+b\tcol{t}+c$の正負を場合分けせよ」という問題$\tcol{t}={\xcol{\Delta x}\over\ycol{\Delta y} }$の変域は実数全体である。$\xcol{\Delta x}=a\cos\alpha,\ycol{\Delta y}=a\sin\alpha$と置けば、${\xcol{\Delta x}\over\ycol{\Delta y} }=\cot \alpha$となる。になり、

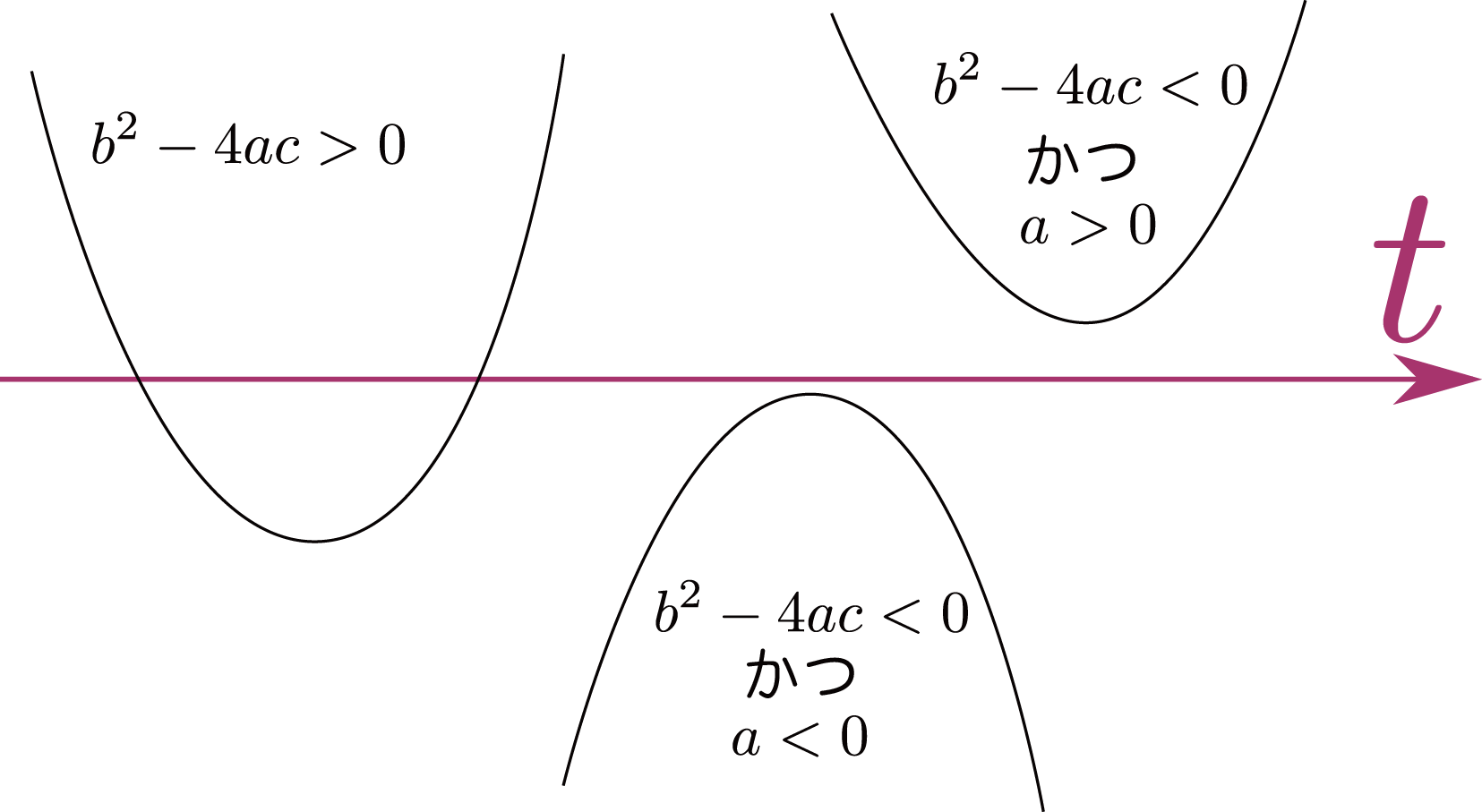
• $b^2-4ac>0$ の場合：　正にも負にもなる（鞍点）
• $b^2-4ac<0$ かつ $a>0$の場合：　常に正（極小点）
• $b^2-4ac<0$ かつ $a<0$の場合：　常に負（極大点）

のように二次方程式の判別式を使うこととで状況を分類することができる$b^2-4ac=0$の場合は省略したが、正（もしくは負）が0以上（もしくは0以下）になるという違いである。。

　この判別式$b^2-4ac$というのは実は$\left(\begin{array}{cc}\opcol{\partial^2 \kuro{f}\over \partial \xcol{x}^2}&\opcol{\partial^2 \kuro{f}\over \partial \xcol{x}\partial {\ycol{y}}}\\[3mm]\opcol{\partial^2 \kuro{f}\over \partial {\ycol{y}}\partial \xcol{x}}&\opcol{\partial^2 \kuro{f}\over \partial {\ycol{y}}^2}\end{array}\right)$という行列（「ヘッセ行列」と呼ぶ）の行列式の$-4$倍である。行列の形で書くと、3変数以上の場合にも拡張できる（作り方のルールは類推できるだろう）。

偏微分の交換可能性

$\opcol{{\partial^2 \kuro{f}\over \partial \xcol{x}\partial \ycol{y}}}$のような「$\xcol{x}$微分と$\ycol{y}$微分が混ざった高階偏微分」について「どっちの微分を先にするのか？」という点が気になるかもしれない。ここで、 \begin{equation} \opcol{\left( {\partial\over \partial \xcol{x}}\kuro{\left(\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\right)}\right)_{\ycol{y}}} =\opcol{\left( {\partial\over \partial \ycol{y}}\kuro{\left(\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\right)}\right)_{\xcol{x}}} \end{equation} であること、すなわち「$\xcol{x}$で偏微分してから$\ycol{y}$で偏微分」と、この順番を変えたものが同じ結果になることただし、これが成立するためには関数が微分可能でなくてはいけないことはもちろんである。を確認しておこう。 \begin{equation} \PDC{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}}{\ycol{y}}{\xcol{x}} = \lim_{\xcol{\Delta x}\to0\atop\ycol{\Delta y}\to0} { f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}+\ycol{\Delta y}} -f\kakko{\xcol{x},\ycol{y}+\ycol{\Delta y}} -f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}} +f\kakko{\xcol{x},\ycol{y}} \over \xcol{\Delta x}\ycol{\Delta y}} \end{equation} である。$\xcol{x}$と$\ycol{y}$の微分の順番を変えると、 \begin{equation} \PDC{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}}{\xcol{x}}{\ycol{y}} =\lim_{\xcol{\Delta x}\to0\atop\ycol{\Delta y}\to0} { f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}+\ycol{\Delta y}} -f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}} -f\kakko{\xcol{x},\ycol{y}+\ycol{\Delta y}} +f\kakko{\xcol{x},\ycol{y}} \over \xcol{\Delta x}\ycol{\Delta y}}\label{DyDxf} \end{equation} を得る。引算の順番が入れ替わっているが、同じ式である。

　図で表現しておこう。省略形で$\PD{}{\ycol{y}}\left(\PD{f}{\xcol{x}}\right)$になる微分を図で表現したのが次の図である。

　一方、$\xcol{x}$と$\ycol{y}$の立場を取り替えた$\opcol{\partial \over \partial \xcol{x}}\left(\opcol{\partial \kuro{f}\over \partial \ycol{y}}\right)$は次の図のように書ける。

　最終結果は、

と、同じ量になっているので、二つの微分は同じになる。別の言い方をすると、操作$\left(\PD{}{\xcol{x}}\fbox{？}\right)_{\ycol{y}}$と操作$\left(\PD{}{\ycol{y}}\fbox{？}\right)_{\xcol{x}}$は交換する。この$\fbox{？}$には何が入ってもよい。三階以上の微分に対しても同じことが言える。

偏微分の注意点

　これに限らず、常微分であれば成立する${\coldy\over \coldx}={1\over {\coldx\over \coldy}}$との類推で、偏微分でも「分母」と「分子」を入れ替える$\left({\partial a\over \partial b}\to {\partial b\over \partial a}\right)$と逆数になる$\left({\partial a\over \partial b}={1\over {\partial b\over \partial a}}\right)$と勘違いしてしまいがちである。

　実際に$\xcol{x},\ycol{y}$を独立変数として$r$を$r\kakko{\xcol{x},\ycol{y}}=\sqrt{\xcol{x}^2+\ycol{y}^2}$としてこれから$\PD{r}{\xcol{x}}$を計算すると、 \begin{equation} \PD{r\kakko{\xcol{x},\ycol{y}}}{\xcol{x}} = \PD{\left(\sqrt{\xcol{x}^2+\ycol{y}^2}\right)}{\xcol{x}} = {1\over 2\sqrt{\xcol{x}^2+\ycol{y}^2}}\times 2\xcol{x}={\xcol{x}\over \sqrt{\xcol{x}^2+\ycol{y}^2}}=\cos\thetacol{\theta} \end{equation} となる。一方で、$\rcol{r},\thetacol{\theta}$を独立変数とすれば$x\kakko{\rcol{r},\thetacol{\theta}}=\rcol{r}\cos\thetacol{\theta}$なので、$ \PD{x}{\rcol{r}}$を計算すると、 \begin{equation} \PD{x\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}} = \PD{\left(\rcol{r}\cos\thetacol{\theta}\right)}{\rcol{r}} =\cos\thetacol{\theta} \end{equation} となる。つまりこの場合$\PD{r}{\xcol{x}}=\PD{x}{\rcol{r}}$なのだ。誤解してしまうのは、省略記法を使っているからである。省略せずに書くと、$\PD{x}{\rcol{r}}$は$\PDC{x\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}{\thetacol{\theta}}$、$\PD{r}{\xcol{x}}$は$\PDC{r\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$である。${\opcol{\biggr)}}_{\thetacol{\theta}}$と${\opcol{\biggr)}}_{\ycol{y}}$の違いに注意。「どの変数を固定しているか」は大事なのである。

　$\PD{\xcol{x}}{\rcol{r}}$を図で表現すると、下のようになる。

　何度も強調しているように、偏微分には方向がある。 $\rcol{r}$方向の微分とは、図にあるような「$\thetacol{\theta}$を一定として変化させる」という微分である。このとき、$\xcol{x}$は$\rcol{\Delta r}\cos\thetacol{\theta}$だけ変化する。

　よって、${\xcol{\Delta x}\over\rcol{\Delta r}}=\cos\thetacol{\theta}$である。

　一方、$\PD{\rcol{r}}{\xcol{x}}$を図で表現したのが次の図である。

　こちらでは、${\rcol{\Delta r}\over\xcol{\Delta x}}=\cos\thetacol{\theta}$である。

　二つの微分は「方向が違う」ということを図を見て納得して欲しい。

　これも、省略記法で書いているせいで「これでいい」と勘違いしてしまうことがある。誤解がないよう省略なしで書けば、常微分の${\mathrm dz\over \mathrm dy}{\mathrm dy\over \mathrm dx}={\mathrm dz\over \mathrm dx}$は${\mathrm dz\kakko{\ycol{y}}\over \mathrm dy}{\mathrm dy\kakko{\xcol{x}}\over \mathrm dx}={\mathrm dz\kakko{y\kakko{\xcol{x}}}\over \mathrm dx}$である一方、偏微分の$\PD{z}{\ycol{y}}\PD{y}{\xcol{x}}\neq\PD{z}{\xcol{x}}$（等式ではないことに注意）は$\PDC{z\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\PDC{y\kakko{\zcol{z},\xcol{x}}}{\xcol{x}}{\zcol{z}}\neq\PDC{z\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\zcol{z}}$であり、本質的に違う計算である。

　$\xcol{x},\ycol{y},\zcol{z}$という3次元の空間を考えて、ある関係式があることによりこのうち二つが独立であったとする。関係があるのだから、三つの変数のうち一つを他の二つで表すことができるつまり、自由度2である。。

　変数の間の関係式を成立させつつ、

1. $\xcol{x}$を一定として$\ycol{y}$を変化（連動して$\zcol{z}$も変化）。
2. $\ycol{y}$を一定として$\zcol{z}$を変化（連動して$\xcol{x}$も変化）。
3. $\zcol{z}$を一定として$\xcol{x}$を変化（連動して$\ycol{y}$も変化）。

という三つの変化を起こして元の場所に戻ってくる経路を考える。

　この図だけでは「立体感」が足りないので、授業では下のような紙工作を使って説明した。

　それぞれの過程において図に描き込んだような分数を計算し、その掛算を行うと、 \begin{equation} {\ycol{\Delta y}\over -\zcol{\Delta z}}\times {\zcol{\Delta z}\over -\xcol{\Delta x}}\times {\xcol{\Delta x}\over -\ycol{\Delta y}}=-1 \end{equation} となる（分母分子に同じものが２回ずつ現れ、分母にマイナスが３回現れる）。極限を取ればこれは \begin{equation} \PDC{y\kakko{\xcol{x},\zcol{z}}}{\xcol{x}}{\zcol{z}}\times \PDC{z\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\times \PDC{x\kakko{\ycol{y},\zcol{z}}}{z}{\ycol{y}}=-1 \end{equation} になる。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。