自然科学のための数学2016年度第5講
グラフの傾きを知る方法
関数の局所的ふるまいを知る
関数を考える時、「ある点の近所での様子」だけを知ればよい、ということがある。この「近所の様子」を「局所的なふるまい」と呼ぼう。逆に全体を見てわかるのが「大局的ふるまい」である。局所的なふるまいを知るには、「その点での値」と「その点での傾き(正確には背線の傾き)」を知れば十分な場合がある。この章で考える微分という計算は「傾き」を知るという目標のためにある。
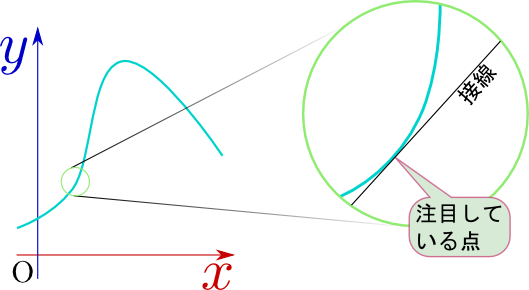
例として、関数$y=x^2+x$を考えよう。この傾きが1であるということを知る方法として、$x^2$の項は$x=0$付近では効かないとして忘れる、という方法がある(これまでの授業で「次数の高い項は関係ない」という話を繰り返ししたのは、この感覚に馴染んでもらうため)。
では、$x=1$付近での傾きを考えるときにはどうしよう。
もちろん、「微分する」ってのが答なんだけど、ここはその微分ってどんな計算か、ということを説明しようと思っているところなので、とりあえず「微分は知らないふり」で考える
やり方1 $x=1$付近で小さいと考えていいのは$(x-1)$だから、この関数を $$ y=x^2+x=(x-1)^2+3(x-1)+2 $$ と書き直し、$(x-1)^2$を無視する。つまり$x=1$付近ではこの関数はほぼ、$y=3(x-1)+2$である。よって傾きは3。
やり方2 我々は$x=0$付近での傾きの計算方法は知っているから、関数を平行移動して$x=1$が原点に来るように変えてしまう $$ y=x^2+x \to y=(x+1)^2+(x+1)=x^2+3x+2 $$ という手もある。この点での傾きはやはり、3である。
やり方3 $x=1$付近で$x$を変化させてみる。$x$の変化量を$\Delta x$とし、$y=x^2+x$がどの程度変化したかを$\Delta y$と表す。傾き(変化率)である${\Delta y\over \Delta x}$を計算して表にすると、
| $x$ | $\Delta x$ | $y=x^2+x$ | $\Delta y$ | ${\Delta y\over \Delta x}$ |
|---|---|---|---|---|
| 2 | 1 | 6 | 0 | 4 |
| 1.1 | 0.1 | 2.31 | 0.31 | 3.1 |
| 1.01 | 0.01 | 2.0301 | 0.0301 | 3.01 |
| 1.001 | 0.001 | 2.003001 | 0.003001 | 3.001 |
| 1 | 0 | 2 | 0 | 3?? |
となる。これを見ると、$x=1$のときの傾きは3になりそうである。
極限としての接線の傾きとしての微分の定義
いちいちこうやって数字で計算するのもたいへんなので、一般的な式を出そう。
一般的な関数$f(x)$に対し、
$f'(x)=\lim_{\Delta x\to0}{f(x+\Delta x)-f(x)\over \Delta x}$
で定義される新しい関数$f'(x)$を「$f(x)$の導関数」とか「$f(x)$の微係数」あるいは、「$f(x)$の微分」と呼ぶ。これが「傾き」を計算する方法である。
微分の定義を、
と書くこともある。実際に使うときはこちらの式を使うことが多い。この式は
という読み方もできる(だから、「微係数」という呼び方をする)。
${\cal O}$は「オーダー」と読み、${\cal O}((\Delta x)^2)$というのは「$\Delta x$の自乗ぐらいの小さい数」ということになる。
${\Delta x}$や${\Delta y}$は「変化量」という意味があった。微分を行う時は、${\Delta x}$を0に近づける(連動して、${\Delta y}$も0に近づく)。このようにここから先の計算ではしばしば、${\Delta x}$や${\Delta y}$に「変化量」という意味に加えて「0に近づく」という属性が加わる。この「0に近づけていく変化量」という量を表すために、新しい記号として$\mathrm dx,\mathrm dy$を導入しよう。
$\mathrm d$という記号
$\Delta$の替りに$\mathrm d $という記号を使って後で$\to0$という極限を取ることが約束されている変化量を示す。
$\mathrm dx$や$\mathrm dy$を「微小変化」と呼ぶが、この呼び方は少し説明が不足していて、単に「微小」ではなく「後で0になる極限を取ることが運命づけられている」という点が重要である。
この「運命」があることで実際の計算上何が違うかというと、「$\mathrm dx$や$\mathrm dy$の二次以上の量(${\cal O}(\mathrm dx^2)$や${\cal O}(\mathrm dy^2)$)を無視する」というルールで計算していけばよい。
$\mathrm dx$や$\mathrm dy$を「微小変化」と呼ぶが、この呼び方は少し説明が不足していて、単に「微小」ではなく「0になる極限を取る」という点が重要である。
あるいは「微小」という考え方がしっくりこない、という人は以下のように考えてもよい。
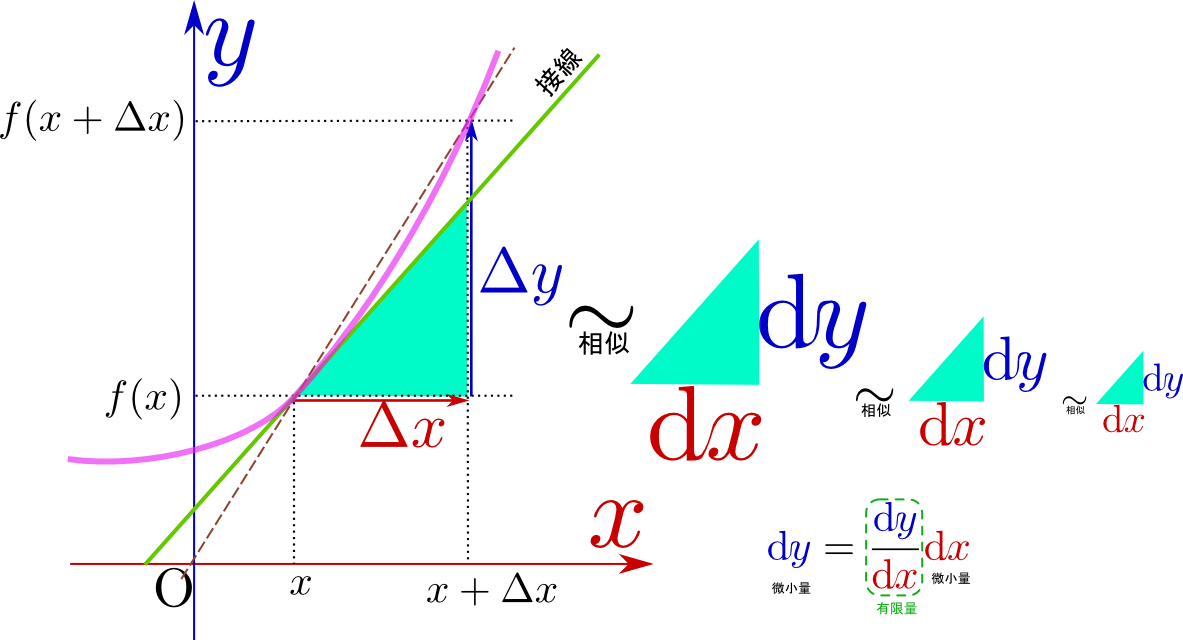
上の図にも示したように、$\mathrm dx$や$\mathrm dy$はあくまで、 のような「接線と同じ傾きを斜辺とした直角三角形」の底辺と高さだと考える(この考え方なら微小である必要はない)。そして、$\mathrm dx$ や$\mathrm dy $そのものの大きさは重要ではなく、
のような「接線と同じ傾きを斜辺とした直角三角形」の底辺と高さだと考える(この考え方なら微小である必要はない)。そして、$\mathrm dx$ や$\mathrm dy $そのものの大きさは重要ではなく、 という形(どんな直角三角形か?)、あるいは「$\mathrm dx$ と$\mathrm dy $の比」が重要であって、$\mathrm dx$ や$\mathrm dy $そのものは大きさを考えてはいけない(考えても意味はない)量とする。いわば、「接線上で定義された長さのようなもの」が$\mathrm dx$ と$\mathrm dy$ であり、それぞれ一つだけでは意味がなく、「$\mathrm dx$ と$\mathrm dy $の二つで向きを表現する量」なのである。
という形(どんな直角三角形か?)、あるいは「$\mathrm dx$ と$\mathrm dy $の比」が重要であって、$\mathrm dx$ や$\mathrm dy $そのものは大きさを考えてはいけない(考えても意味はない)量とする。いわば、「接線上で定義された長さのようなもの」が$\mathrm dx$ と$\mathrm dy$ であり、それぞれ一つだけでは意味がなく、「$\mathrm dx$ と$\mathrm dy $の二つで向きを表現する量」なのである。
${\mathrm dy\over \mathrm dx}$は普通の数(大きさを考える意味がある)だし、$\mathrm dy=a\mathrm dx$と書いた時の$a$も普通の数である。だから${\mathrm dy\over \mathrm dx}=2$や$\mathrm dy = 0.7\mathrm dx$は意味のある式である。しかし、$\mathrm dx=1$とか$\mathrm dy=0.02$などという式には全く意味がない=0だけは、「$\mathrm dx=0$の極限をとって」のように使うこともあるが、本来はあまりよい使い方ではない。。$\mathrm dy$ や$\mathrm dx $は、二つがペアになって接線の向きを表現している量であって、$\mathrm dx$ のみの大小を云々してはいけない。
新しい記号を使えば、接線の傾きは${\mathrm dy\over \mathrm dx}$になる$\mathrm dx$や$\mathrm dy$は、接線という直線の上での長さを表現しているという考え方もできる。。この${\mathrm dy\over\mathrm dx}$、厳密に書けば
\begin{equation} {\mathrm dy\over\mathrm dx}=\lim_{{\Delta x}\to0}{{\Delta y}\over {\Delta x}} \end{equation}が導関数(もしくは微係数)である。$\mathrm dy$ と$\mathrm dx $は微小量、すなわち0になる極限を取るべき量だが${\mathrm dy\over \mathrm dx}$は有限な量である。
こうして「傾き」という量を$x$の関数として表現する方法を我々は得た。最初に書いた${{\Delta y}\over {\Delta x}}$という量は、ある「幅」${\Delta x}$があって(その「幅」の間での変化の割合として)初めて定義できる量だったが、${\mathrm dy\over \mathrm dx}$の方は、「一点」$x$で決まる量であることに注意しよう。
これが導関数(もしくは微係数)を${\mathrm dy\over \mathrm dx}(x)$のように書く理由である。f'(x)の方はニュートンによる記号で、$f$という関数から$f'$を作ったということをよく表現できている記号である。一方${\mathrm dy\over \mathrm dx}$はライプニッツの記号で、何の変化と何の変化の比を考えているのかがよく表現できている記号である。これらの記号は使いどころによって一長一短がある。
$\mathrm d$を使った計算の練習
新しい記号$\mathrm d$を使って微分の計算を行ってみよう。
この記号を使うと、$f(x+\mathrm dx)=f(x)+f'(x)\mathrm dx$のように表すことができる。
$f(x)=x^2$の微分を例としよう。まず、 $$ y=x^2 $$ と、これを微小変化させた $$ y+\mathrm dy=(x+\mathrm dx)^2 $$ を考える。この二つの式から、 \begin{equation} \mathrm dy=2x\mathrm dx+(\mathrm dx)^2 \end{equation} がわかる。この式の$\mathrm dx\to0,\mathrm dy\to0$の極限を考えると
\begin{equation} \underbrace{ \mathrm dy}_{\to0} = \underbrace{2x\mathrm dx}_{\to0} + \underbrace{(\mathrm dx)^2}_{\to0} \end{equation}となって0=0という「当たり前すぎてつまんない(trivialな)式」が出る。何の情報も引き出せない。$\mathrm dy$と$\mathrm dx$の比のみが重要なのだから、まず両辺を$\mathrm dx$で割って
\begin{equation} {\mathrm dy\over\mathrm dx} = 2x + \mathrm dx \end{equation}とした後に$\mathrm dx\to0$という極限を取ることで、以下の式を得る。
\begin{equation} {\mathrm dy\over\mathrm dx} = 2x \end{equation}「$\mathrm dx$というのは$\mathrm dx\to0$という極限を取られることを運命づけられている量であることを考えると、右辺第二項の$(\mathrm dx)^2$をこれ以上計算する必要はない」と考えて
\begin{equation} \mathrm dy= 2x\mathrm dx \end{equation}として${\mathrm dy\over\mathrm dx}=2x$を出してもよい。というより慣れてきたらそうするべきである。
$2x\mathrm dx$も$(\mathrm dx)^2$も、$\mathrm dx\to0$とすれば$0$になるのは同じなのに、$(\mathrm dx)^2$の方だけを消す理由は何ですか?
$2x\mathrm dx$と$(\mathrm dx)^2$を比較して、「$(\mathrm dx)^2$の方が速く0になる」という判断で消す。具体的には$\mathrm dx$の次数を考える。$2x\mathrm dx$は$\mathrm dx$の1次、$(\mathrm dx)^2$は$\mathrm dx$の2次である。
あくまで「小さい物+もっと小さい物」という形になっている時に「もっと小さい物」の方が消せるのだ、ということに注意しよう。
$y=x^2$の両辺を微小変化させると
\begin{equation} y+\mathrm dy = (x+\mathrm dx)(x+\mathrm dx) \end{equation}になる。そして「あ、この中には$x\mathrm dx$が2個あるな」と考えれば、右辺は$x^2+2x\mathrm dx$となる。
$y=x^3$の微分は、
\begin{equation} y+\mathrm dy = (x+\mathrm dx)(x+\mathrm dx)(x+\mathrm dx) \end{equation}として、右辺に$x^2\mathrm dx$が三つある、ということを数えれば、
\begin{equation} \mathrm dy = 3x^2 \mathrm dx \end{equation}
となる。そしてこれから$y'={\mathrm dy\over \mathrm dx}=3x^2$である。
今日の小テスト
導関数が求められたら、$x=0$では1、$x=1$では3になることを確認せよ。
解答は以下の通り。まず$y=x^2+x$に$y\to y+\mathrm dy,x\to x+\mathrm dx$を代入する。
$$
y+\mathrm dy=(x+\mathrm dx)^2+(x+\mathrm dx)
$$
を計算して、
$$
y+\mathrm dy=x^2+x+(2x+1)\mathrm dx+\underbrace{(\mathrm dx)^2}_{無視してよい部分}
$$
となる。これを見て$\mathrm dx$の係数を見てすぐ「導関数は$2x+1$と判断してもよいし、
$$
{\mathrm dy\over\mathrm dx}=2x+1
$$
と計算してもよい。
これから、$x=0$では1、$x=1$では3となることはすぐにわかる。