微分の性質・公式など(続き)
合成関数の微分
このルールは「連鎖律(chain rule)」とも呼ばれる。数式で表現しておこう。$g(f(x))$という合成関数を考えて、その独立変数$x$を$x+\mathrm dx$と微小変化させると、 \begin{equation} f(x+\mathrm dx)= f(x)+ \underbrace{f'(x)\mathrm dx}_{\mathrm d(f(x))} \end{equation} のように$f(x)$が変化する。ここで$\mathrm d (f(x))=f'(x)\mathrm dx$という記号を使った。$\mathrm d(なんとか)$のように$\mathrm d$をつけることで(なんとか)の微小変化という意味を持たせるこれをさらに省略して$\mathrm df(x)$、さらに$(x)$も省略して$\mathrm df$とだけ書いたりもする。。ライプニッツの記号では、$\mathrm d (f(x))={\mathrm df\over \mathrm dx}(x)\mathrm dx$と書けて、「$\mathrm dx$を約分している」というイメージで捉えることができる。
$f(x)$の$x$が微小変化すると、$g(f(x))$は \begin{equation} g(f(x+\mathrm dx))= g(f(x))+f'(x)\mathrm dx \end{equation} と微小変化する。上にも書いたように、$f'(x)\mathrm dx$の部分を$\mathrm dx(f(x))$と考えれば、上の式の$f(x)$の部分を$f$という変数に置き換え、$f$が$\mathrm df$すなわち$\mathrm d(f(x))$だけ変化していると解釈して \begin{equation} g({f}+\mathrm df)= g(f)+g'({f})\mathrm df \end{equation} と書く。この$g'({f})$はもちろん$g({f})$を${f}$で微分した結果である。${f}$を元の関数$f(x)$に戻すと \begin{equation} g(f(x)+\mathrm d(f(x)))= g(f(x))+g'(f(x))\overbrace{f'(x)\mathrm dx}^{\mathrm d(f(x))} \end{equation} なので、$g(f(x))$の導関数が$g'(f(x))f'(x)$だとわかる。
これを、 $$ {\mathrm dg(f(x))\over\mathrm dx}={\mathrm g(f)\over \mathrm df}\times{\mathrm df(x)\over\mathrm dx} $$ のように「約分」しているように書く。
$x\to{y}\to{z}$(${y}=f(x),{z}=g({y})$)という関係がある時、$x$を微小変化させた時にそれに応じて${y}$が、さらに連鎖して${z}$が変化する様子を立体図で表現しよう。
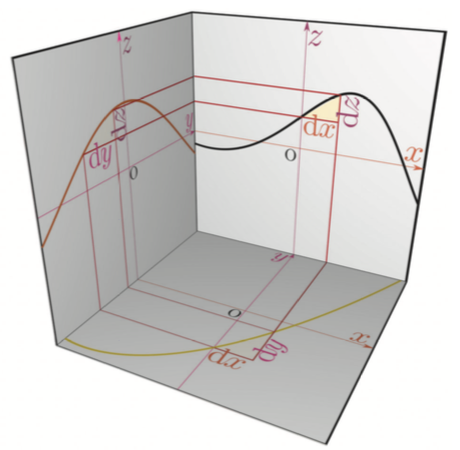
上図に${\mathrm dy\over \mathrm dx}(x),{\mathrm dz\over \mathrm dy}({y}),{\mathrm dz\over \mathrm dx}(x)$の三つの導関数に対応する三角形(この三角形の傾きが導関数の値)が描かれている。導関数は$\mathrm dx,\mathrm dy,\mathrm dz$という三つの微小量の比でここでも計算しているのは微小変化の「比」だけであって、微小変化そのものではない。計算されるものだから、 \begin{equation} \begin{array}{c} {\mathrm dz\over \mathrm dy}(y) {\mathrm dy\over \mathrm dx}(x)={\mathrm dz\over \mathrm dx}(x)\\ ただし、{y}=f(x) \end{array} \end{equation} が成立する。この計算は、${\mathrm dz\over {\mathrm dy}}{{\mathrm dy}\over \mathrm dx}={\mathrm dz\over \mathrm dx}$という「約分」を行った、と解釈できる。
くどいようだが、もう一度確認しておこう。${\mathrm dy\over\mathrm dx}$は「分数」の形で書いているが普通の意味の割算ではない。しかし「比の極限」ではあるので、分数と同様に約分ができるという性質は持っている(「割り算ではない」と言われからといって、割り算でできること全てをあきらめる必要はないのであるこれに限らず何事も、「0か1か」のような極端な判断をしないようにしよう。)。そういう意味で、この計算を「約分」と見ることは正しい。
例として$f(x)=((x)^2+x)^3$の微分をしてみよう。これを$f(y)={y}^3,{y}=g(x)=x^2+x$として、$f(x)=f(g(x))$と考えてから微分すると、 \begin{equation} {\mathrm d\over\mathrm dx} f(x)=\underbrace{ {\mathrm d\over\mathrm dx} g(x)}_{2x+1} \underbrace{ {\mathrm dx \over \mathrm dy}f({y})}_{3{y}^2} = 3(2x+1)\underbrace{(x^2+x)^2}_{{y}^2} \end{equation} となる。慣れてきたら${y}$を導入するのも省略して、 \begin{equation} \overbrace{ \mathrm dx \left((x^2+x)^3\right)}^{\fbox{?}^3の微分} =\overbrace{3 (x^2+x)^2}^{3\fbox{?}^2} \times\overbrace{ \mathrm d (x^2+x)) }^{\fbox{?}の微分}=3(2x+1)(x^2+x)^2\mathrm dx \end{equation} のように計算してよい。
いくつかの公式
分数関数の微分
${y}={1\over f(x)}$の微分は、上でやったように、まず${y}f(x)=1$と直してから \begin{equation} \begin{array}{rll} {y}f(x)=&1&{↓微分}\\[-2mm] \underbrace{\mathrm dy}_{前を微分}f(x)+{y}\underbrace{f'(x)\mathrm dx}_{後を微分} =&0&{↓移項}\\ \mathrm dy f(x)=& -\overbrace{{1\over f(x)}}^{{y}}f'(x)\mathrm dx\\ {\mathrm dy\over \mathrm dx}=& -{f'(x)\over \left(f(x)\right)^2} \end{array} \end{equation} として計算することができる。
逆関数の微分
「逆数の微分」ではないので間違えないように(この二つは全く違う)。関数${y}=f(x)$の逆関数$x=f^{-1}({y})$を微分するとどうなるか、という問題である。導関数は$ {従属変数の微小変化\mathrm dy \over 独立変数の微小変化\mathrm dx}$という比で計算される。${\mathrm dy\over \mathrm dx}=f'(x)$なのだから、${\mathrm dx\over \mathrm dy}={1\over f'(x)}$なのは当たり前である(どちらも、$\mathrm dy=f'(x)\mathrm dx$を変形すれば得られる)。
三角関数の微分
準備:三角関数の極限
前にグラフで示した(しかしまだその根拠は示してない)ように、$\sin x$は$x=0$付近では$x$とほぼ同じ(傾き1)である。すなわち$\lim_{\Delta x\to0}{\sin\Delta x\over \Delta x}=1$である。
$x$が小さいときに$\sin x\simeq x$であることは、電卓による計算で確認した。以下で図解をもう少し詳細に行おう。
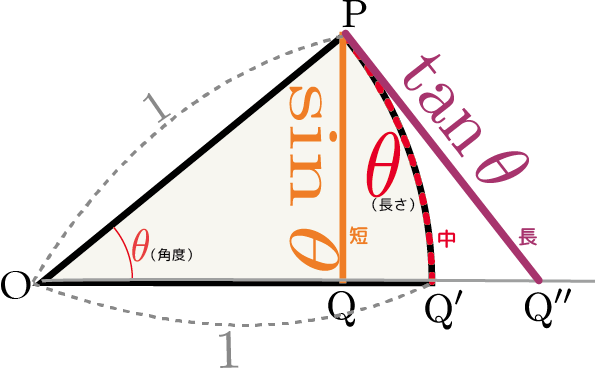
上の図は半径1で中心角$\theta$の扇型である。扇型の「弧」の部分の長さも$\theta$となる(これはラジアンという角度の定義)。一方、$\sin{\theta}$というのは図に描かれた線分「PQ」に対応する。図には$\tan{\theta}$、すなわち「底辺1の直角三角形の{高さ}」も示した(この時の「底辺」は図のOPであることに注意)。ここでこの$\theta$をどんどん小さくしていくところを想像して欲しい。当然、$\sin {\theta}$と$\tan{\theta}$も小さくなる($\theta\to0$の極限で全て0になるだろう)。
$\theta$が0付近の小さい角度であるとき、 \begin{equation} \sin {\theta}<\theta<\tan{\theta} \end{equation} という関係がある。それを示すには、$\sin\theta,\theta,\tan \theta$の三つは、図に示した三つの経路を伝わって点${\rm P}$から点${\rm Q}$、点${\rm Q'}$、点${\rm Q''}$へと向かう線(真ん中のだけは曲線で、残り2本は直線)の長さであることを使う。
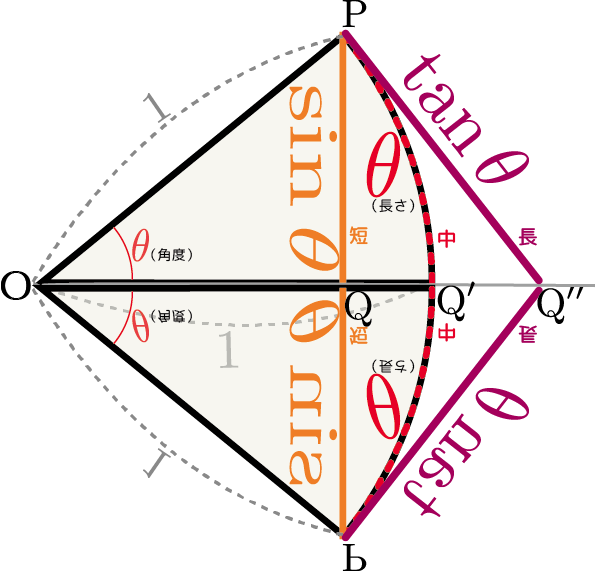
上の図のように鏡像を持ってきて、${\rm P}$の鏡像にあたる点までの経路を考える(これらの経路の長さは上で考えた長さのそれぞれ2倍となる)。三つの経路の中で、一番「まっすぐ」進んでいる${\rm P}\to {\rm Q} \to {\rm P}の鏡像$が一番短く、${\rm P}\to {\rm Q'}\to{\rm Pの鏡像}$が中間、もっとも「遠回り」している${\rm P}\to{\rm Q''}\to{\rm P の鏡像}$が一番長い。
以上の説明でなお納得できないという人は、微分の精神である「まず狭い範囲で考える」をここでも活用して考えよう。
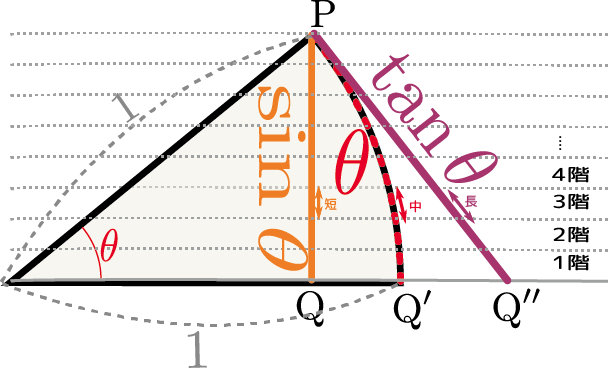
上の図に点線で示したように三角形を$n$階建てのビルだと考え、各々の階での線の長さを見る。各階の高さを小さくすれば($n$階建ての$n$が無限に大きい極限を考えれば)全ての線はほぼ直線であるから、線の鉛直に対する傾きを見ることで、線の長さが
${\sin\theta の一部}<{\thetaの一部}<\tan{\thetaの一部}$ 
だとわかる。
全体の長さは各階での長さの和だから、$\sin {\theta}<\theta<\tan{\theta}$が得られて、これを正の数である$\theta$で割ることで、 \begin{equation} {\sin \theta\over \theta}< 1 < \overbrace{{\sin \theta\over \theta}\times {1\over \cos \theta}}^{{\tan \theta\over \theta}} \end{equation} という式を作ることができて、さらにこの式の右側の部分である$1 < {\sin \theta\over \theta}\times {1\over \cos \theta}$に正の数$\cos\theta$を掛けると$\cos \theta<{\sin \theta\over \theta}$が得られるから、 \begin{equation} \cos \theta< {\sin \theta\over \theta}< 1 \end{equation} が結論できる。この式を作ってから$\theta\to0$という極限を取ると、$\cos \theta\to1$だから、$\cos \theta$と1の間に挟まれた${\sin \theta\over \theta}$も1に近づく$\left(\lim_{\theta\to0}{\sin \theta\over \theta}=1\right)$。これで、 \begin{equation} \sin \theta\fallingdotseq \theta~~~~~より正確には、 \sin \theta=\theta+{\cal O}(\theta^3) \end{equation} がわかった残りの部分が${\cal O}(\theta^2)$ではなく${\cal O}(\theta^3)$なのは、$\sin$が奇関数($\sin (-\theta)=-\sin \theta$)だから。$(\theta^2)$に比例する項はない。。
三角関数の導関数
$\sin$の導関数
三角関数の加法定理 \begin{eqnarray} \sin (A+B)=\sin A\cos B+\cos A\sin B\\ \cos (A+B)=\cos A\cos B-\sin A\sin B \end{eqnarray}
の$\sin$の方を使って \begin{equation} \sin (\theta+\mathrm d\theta)=\sin \theta \cos \mathrm d\theta+\cos \theta \sin \mathrm d\theta \end{equation} という式を出す。$\mathrm d\theta$は0に近づけるのだから$\mathrm d\theta$の1次までのオーダーまでしか見ないことにすると$\sin \mathrm d\theta =\mathrm d\theta,\cos\mathrm d\theta=1$であるから、 \begin{equation} \sin (\theta+\mathrm d\theta)= \sin \theta+\overbrace{\cos \theta}^{微係数}\mathrm d\theta \end{equation} となる。$f(x)+\mathrm dx=f(x)+f'(x)\mathrm dx$と比較することにより、以下がわかる。
$\sin$の導関数 \begin{equation} \begin{array}{rl} {\mathrm dx }(\sin \theta)=&\cos\theta \mathrm d\theta,~~~~ \mathrm d\theta(\sin \theta)=\cos\theta \end{array} \end{equation}
次に、同じことを図で考えよう。
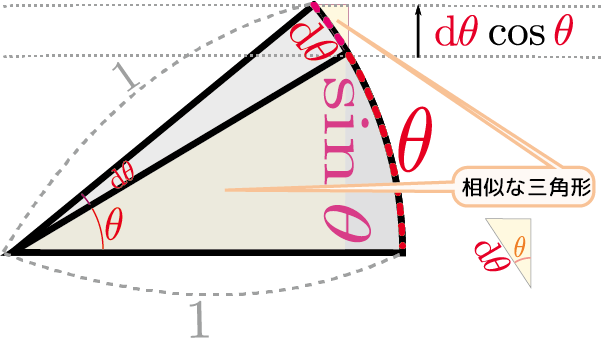
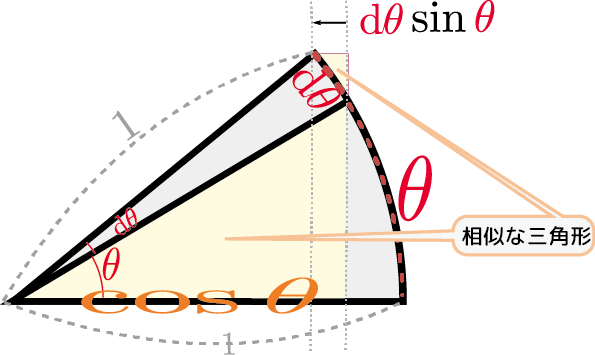
上の図のように、角度$\theta$を$\mathrm d\theta$だけ変化させた時の、「三角形の高さ」である$\sin\theta$の変化を考える。図に「相似な三角形」として示している「小さい方の三角形の斜辺は曲線だから相似な三角形とは言えないぞ!」と思う人もいるかもしれないが、今$\mathrm d\theta$をどんどん小さくしているので、この曲線は限りなく直線に近い。ように、$\mathrm d\theta$ という長さの弧を斜辺として微小な直角三角形ができていて、この直角三角形の高さにあたる部分が$\mathrm d\theta \cos\theta$である。$\sin \theta$の微小変化が$\cos \theta\mathrm d\theta$と書けるから、微係数は$\cos \theta$である。
$\cos$の導関数
$\sin $と同じ手順で考えることができる。三角関数の加法定理を使って、 \begin{equation} \begin{array}{rll} \cos (\theta+\mathrm d\theta) =&\cos \theta \underbrace{\cos \mathrm d\theta}_{1} - \sin \theta \underbrace{\sin \mathrm d\theta}_{\mathrm d\theta}=\cos \theta\underbrace{- \sin \theta}_{微係数} \mathrm d\theta \end{array} \end{equation} を得るから、$\mathrm d\theta(\cos \theta)= -\sin \theta$となる。
こちらも下のように図解することもできる。符号マイナスがつくのは、減る方向(図の左へ)の変化だからである。