指数関数の微分
指数関数${y}=a^{{x}}$を微分することを考えよう。まずは数式で「微分の定義」までちゃんと戻って考える。実は$a=\mathrm e$の時が一番簡単なので、まずはその場合を考えよう。
\begin{equation}
{\mathrm d \over \mathrm dx }\left(\mathrm e^{x}\right)= \lim_{{\Delta x}\to0}{\mathrm e^{{x}+{\Delta x}}-\mathrm e^{x}\over {\Delta x}}
=\mathrm e^{x} \times\lim_{{\Delta x}\to0}{\mathrm e^{{\Delta x}}-1\over {\Delta x}}
\end{equation}
のように、極限の式から$\mathrm e^x$を外に出してしまう。こんなふうに外に出てしまうのは、指数関数という関数が「${x}$が${\Delta x}$増加すると「元の値」の$\mathrm e^{{\Delta x}}$倍になる」という性質を持っている(ということはつまり、増加量も元の関数の値に比例する)ということの顕れである。
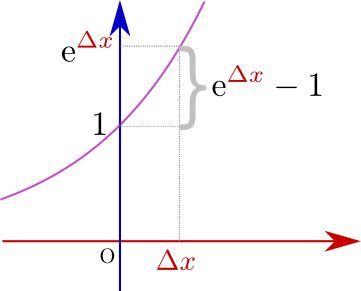
残った部分$\lim_{{\Delta x}\to0}{\mathrm e^{{\Delta x}}-1\over {\Delta x}}$はよく見ると${x}$によらない定数になっている。そしてこれは、${y}=\mathrm e^{x}$の${x}=0$での傾きそのものである(右のグラフ参照)。そしてそれは$\mathrm e$の定義により1である。つまり、
\begin{equation}
{\mathrm d \over \mathrm dx }\left( \mathrm e^{{x}}\right)=\mathrm e^{x}\label{expbibun}
\end{equation}
なのである。$\mathrm e^x$という関数は「微分しても変わらない関数」であった、ということがわかる(だから$\mathrm e$は重要なのである)。
「微分しても変わらない関数ってどんなもの?」という視点から、指数関数を「導いて」みよう。まず我々は$\mathrm e^{{x}}$の${x}=0$での値が1で傾きが1であること、つまり${x}=0$の近傍では$\mathrm e^{x}=1+{x}$であることを知っている。しかし、$1+{x}$を微分すると
\begin{equation}
{\mathrm d \over \mathrm dx }\left(1+{x}\right)\stackrel{?}{=}1
\end{equation}
となって元に戻らない。微分した後に${x}$がいるためには、関数に${1\over 2}{x}^2$を加えておくとよいだろう。しかし、
\begin{equation}
{\mathrm d \over \mathrm dx }\left(1+{x}+{1\over 2}{x}^2\right)\stackrel{?}{=}1+{x}
\end{equation}
であるからこれでは微分すると(右辺に${1\over 2}{x}^2$が足りない分)元に戻らない。ではということでさらに${1\over 2\times3}{x}^3$を加える。すると、
\begin{equation}
{\mathrm d \over \mathrm dx }\left(1+{x}+{1\over 2}{x}^2+{1\over 2\times3}{x}^3\right)\stackrel{?}{=}1+{x}+{1\over 2}{x}^2
\end{equation}
となる。この手順を繰り返していくと考えれば、
\begin{equation}
\begin{array}{rl}
\mathrm e^{{x}}=&1+{x}+{1\over 2}{x}^2+{1\over 2\times3}{x}^3
+{1\over 2\times 3\times 4}{x}^4+{1\over 2\times 3\times 4\times 5}{x}^5
+\cdots\\
=&\sum_{n=0}^\infty {1\over n!}{x}^n
\end{array}
\end{equation}
という無限につづく項の和で書ける、ということになる。前に$1+1+{1\over2}+{1\over 2\times3}+{1\over 2\times 3\times 4}+{1\over 2\times 3\times4\times 5}+\cdot$という計算で$\mathrm e$が出せる、という話をしたが、その理由はこれである。
次に$\mathrm e^{kx}$のように指数が定数$k$倍されている場合を考えると、
\begin{equation}
{\mathrm d (\mathrm e^{kx})\over \mathrm dx }=
\lim_{{\Delta x}\to0}{\mathrm e^{kx+k{\Delta x}}-\mathrm e^{kx}\over {\Delta x}}
=\mathrm e^{kx}\lim_{{\Delta x}\to0}{\mathrm e^{k{\Delta x}}-1\over {\Delta x}}
\end{equation}
となるが、
\begin{equation}
\lim_{{\Delta x}\to0}{\mathrm e^{k{\Delta x}}-1\over {\Delta x}}=
\lim_{{\Delta x}\to0}{\mathrm e^{k{\Delta x}}-1\over {k{\Delta x}\over k}}
= k\lim_{{\Delta x}\to0}{\mathrm e^{k{\Delta x}}-1\over {k{\Delta x}}}
\end{equation}
としてから$k{\Delta x}=t$と置くとこの式はさらに$k\lim_{t\to0}{\mathrm e^{t}-1\over {t}}$と書き直せて、この極限は$k$だから、
\begin{equation}
{\mathrm d (\mathrm e^{kx})\over \mathrm dx }= k\mathrm e^{kx}
\end{equation}
となる(このような状況を「$k$が$\exp$の肩から降りてくる」と表現する)。
ここまでくると、底が$\mathrm e$ではなく一般の正の数であった場合も同様に、$a=\mathrm e^{\log a}$と書けることを使って$a^{{\Delta x}}=\mathrm e^{{\Delta x} \log a}$と直して考えて、
一般の指数関数の微分
\begin{equation}
{\mathrm d (a^x)\over \mathrm dx }= a^x \log a
\end{equation}
がわかる($a=\mathrm e$なら、$\log\mathrm e=1$だから${\mathrm d (\mathrm e^x)\over \mathrm dx }= \mathrm e^x$に戻る)。
いくつかの関連する式が出てきた時、一個一個別々にではなく「この式はあの式をこうすると出てくる」のようなつながりを意識して理解していくことは大事。人間の脳の記憶容量は有限なので、できる限り「こことここは同じ」というところはまとめておいた方が効率がいいし、つながりを知ることはその式の意味をより深く理解することにつながる。
対数関数の微分
${y}=\log{x}$を微分するには、まず$\mathrm e^{y}={x}$として、
\begin{equation}
\begin{array}{rl}
\mathrm e^{y}=&{x} \\
\underbrace{\mathrm e^{y}}_{{x}}\mathrm dy =&\mathrm dx \\
{\mathrm dy \over \mathrm dx }=& {1\over {x}}
\end{array}
\end{equation}
とすればよい(もちろん、$\mathrm e^{{x}}$の逆関数だから${1\over \mathrm e^{{x}}}$になると考えてもよい)。
対数関数の微分
\begin{equation}
{\mathrm d \over \mathrm dx }(\log{x})={1\over x}~~~(これは底が\mathrm e の時に限る)
\end{equation}
前に、${x}^\alpha$のような冪の形で、微分して${1\over {x}}$になる関数はない、という話をしたが、$\log{x}$というのがそういう関数になる。
この式と合成関数の微分則から、$\log \left(f({x})\right)$の微分は
\begin{equation}
{\mathrm d \over \mathrm dx }\log \left(f({x})\right)
=f'({x})\times {\mathrm d \over \mathrm df}\log|f|=
{f'({x})\over f({x})}
\end{equation}
となる。これから、
\begin{equation}
f'({x})=f({x})\times {\mathrm d \over \mathrm dx }\log \left(f({x})\right)
\end{equation}
のように微分の計算を行うことができる(つまり、$\log$を取ってから微分して元の関数を掛けることで微分ができる)。
ややこしくなりそうに思うかもしれないが、対数の性質のおかげでこれで楽ができる状況もある。というのは、関数の積$f({x})g({x})$の微分はライプニッツ則を使うと、
\begin{equation}
{\mathrm d \over \mathrm dx }\log \left(f({x})g({x})\right)={\overbrace{f'({x})g({x})+f({x})g'({x})}^{(f({x})g({x}))'}\over f({x})g({x})}\label{taisuubibunkihon}
\end{equation}
積の対数が対数の和になることを使うと
\begin{equation}
{\mathrm d \over \mathrm dx }\log \left(f({x})g({x})\right)=
{\mathrm d \over \mathrm dx }\log \left(f({x})\right)
+ {\mathrm d \over \mathrm dx }\log \left(g({x})\right)={f'({x})\over f({x})}
+{g'({x})\over g({x})}
\end{equation}
となり、この二つは(当たり前だが)一致する。
また、${y}={x}^{{x}}$のようなややこしい冪で表された関数も、対数を取ってから微分する方法が楽である。
\begin{equation}
{\mathrm d \over \mathrm dx }\left(\log{x}^{{x}} \right)
={\mathrm d \over \mathrm dx }\left(
{x}\log{x}
\right)
=\log{x}+{x}\times {1\over {x}}=\log{x}+1
\end{equation}
のように微分して、
\begin{equation}
{\mathrm d \over \mathrm dx }{x}^{{x}}={x}^{{x}}\times \left(\log{x}+1\right)
\end{equation}
とする。
過去にあった、よくある間違い
${\mathrm d \over \mathrm dx }\left(x^x\right)=x x^{x-1}=x$
↑やってしまわないよう、注意。
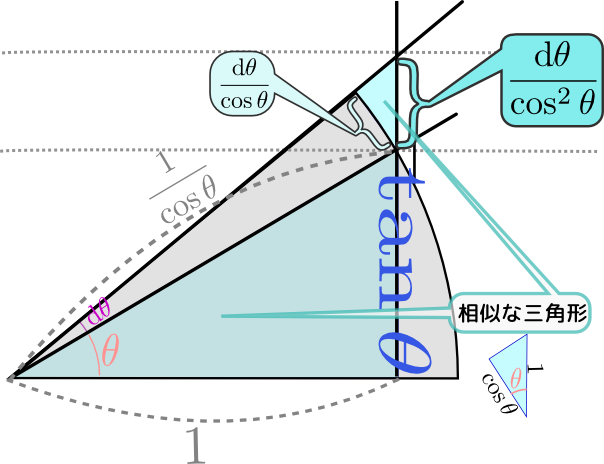
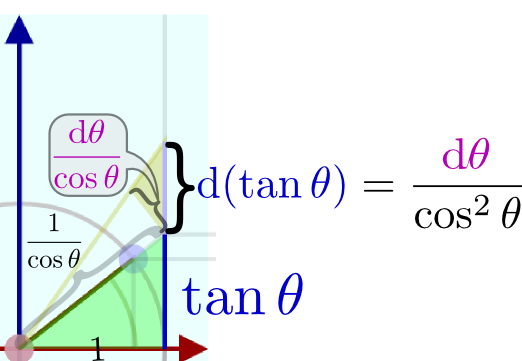
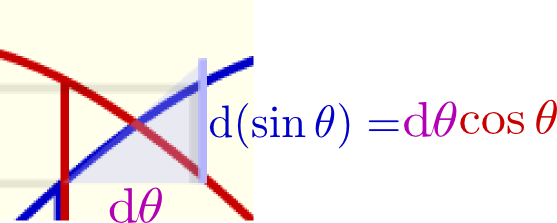 のように傾きが表示してある。この「傾き」が確かにcosθに比例していることを確認しよう。
のように傾きが表示してある。この「傾き」が確かにcosθに比例していることを確認しよう。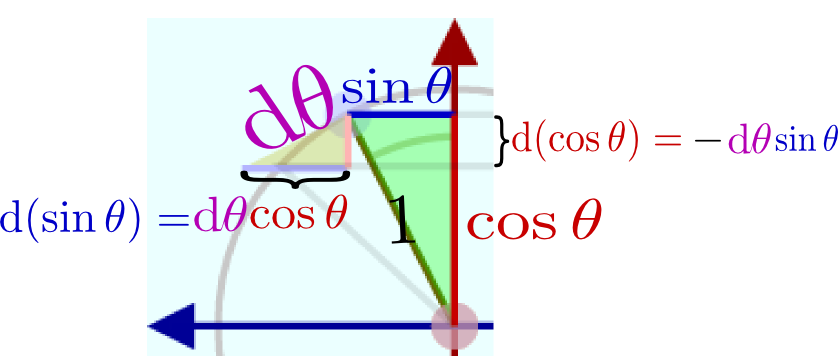
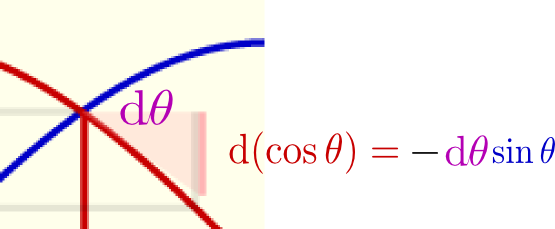 のように表示されている。これも動径をドラッグすることができるので、動かしながら「
のように表示されている。これも動径をドラッグすることができるので、動かしながら「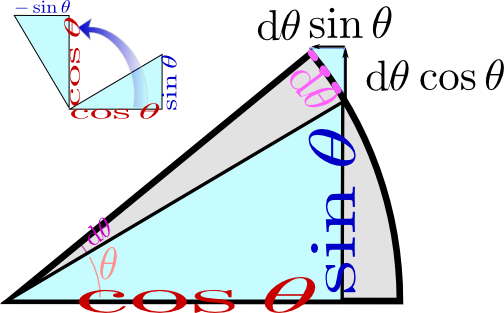
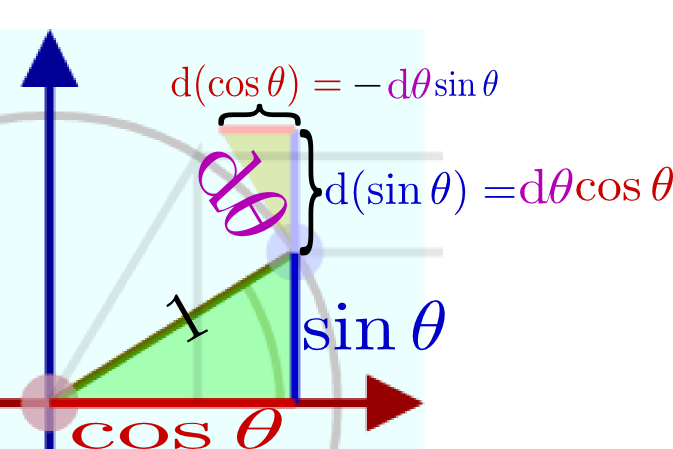
 のように、$x$座標を$y$座標に、$y$座標を(符号を変えて)$x$座標にすることで得られる。式で書くなら$(x,y)\to(-y,x)$であるが、これが微分$(\cos \theta,\sin \theta)\to(-\sin \theta,\cos \theta)$と同じ計算になっているわけである
のように、$x$座標を$y$座標に、$y$座標を(符号を変えて)$x$座標にすることで得られる。式で書くなら$(x,y)\to(-y,x)$であるが、これが微分$(\cos \theta,\sin \theta)\to(-\sin \theta,\cos \theta)$と同じ計算になっているわけである