$\def\coldr{\rcol{\mathrm dr}}\def\coldvecx{\xcol{\mathrm d\vec x}}\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{~~~~~~~{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}\def\kidy{\opcol{\diff y}}\def\ve{\vec{\mathbf e}}\def\colvecx{\xcol{\vec x}}\definecolor{usuopcolor}{RGB}{237,234,203}\def\usuopcol#1{\color{usuopcolor}#1}\def\vgrad#1{{\usuopcol{\overrightarrow{\opcol{\rm grad}~\kuro{#1}}}}}\def\dX{\rcol{\mathrm dX}}\def\dY{\thetacol{\mathrm dY}}$
物理などの自然科学を探求していくとき、
ある量$\xcol{A}$を変化させた時に、それとは別のある量$\ycol{B}$がそれに応じてどう変化するか?
を調べていかなくてはいけないことがよくある。この$\xcol{A}$から$\ycol{B}$への関係}($\xcol{A}\to \ycol{B}$)のことを「関数(function)」と呼ぶ。「数」に限らず「何かを入力(インプット)したら何かが出力(アウトプット)される」働きを持っていればそれは「function(関数)」と呼んでも良い。数学的な意味で「関数」と言うときは数(もしくは数で表現できる量)を相手にしていることが多いが、数学だからと言って「数」を扱っているとは限らない。
関数のインプットとアウトプットにあたる量を「変数(variable)」}と呼ぼう。まず最初に変化させるある量$\xcol{A}$は「独立変数(independent variable)」、それに応じて変化するある量$\ycol{B}$は「従属変数(dependent variable)」と呼ぶ。
互いに関係のある量を計測する実験を何度も行うことによってそれぞれの量の間にどのような法則があるかを求めていこうとすることが自然科学の始まりだ。計測するものは数であることが多いので、ある数$\to$また別のある数という対応関係(「関数」)を調べていくことが多くなる。
関数をグラフで表現する
$\xcol{x}$と$\ycol{y}$に$\xcol{x}$を1つ決めれば$\ycol{y}$が1つ決まるという関係があるとき、「$\ycol{y}$は$\xcol{x}$の関数だ」と言う。関数の対応関係は式で表してもよいが、次のグラフのように表現してもよい。たとえばこの関数が$\ycol{y}=f\kakko{\xcol{x}}$という式で表現されるものであったならば、グラフの線の上では$\ycol{y}=f\kakko{\xcol{x}}$が成り立ち、それ以外の場所では成り立たない。
つまりグラフが表現している「線」は「$\ycol{y}=f\kakko{\xcol{x}}$が成り立つ点」の集合だ。多くの場合、これはある線になるが、関数が変な関数であれば、「線」になるとは限らない。線になるかどうかは、関数が連続性を持つかどうかによる。連続性があればある点の「隣」に点があるから、関数の式を満たす点の集合が「線」になる。実験などで測定値をグラフに「点」でプロットして、最後に「えいやっ」と線を引くが、それは考えている関数が連続であることを仮定(期待)しているからだ。なお、図でもそうだが逆の$\ycol{y}$を1つ決めれば$\xcol{x}$が1つ決まるの方は成立しなくてもよい。
双曲線は関数ですか?
双曲線って、
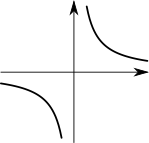
のこと? これは関数だけど。
いえ、
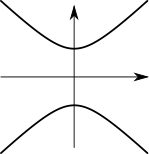
です。
ああ、それは$\xcol{x}$一つに$\ycol{y}$が二つあるから関数じゃないね。
実は

も、$\xcol{x}=0$の点では対応する$\ycol{y}$がない(定義されてない)から、そこ以外では関数という、制限付きの関数です。
ちょうどいい質問が来たので定義域と値域について説明しておこう。
状況により$\xcol{x}$はなんでもよいわけではなく、「定義域(domain of definition)」と呼ばれる範囲に入っていなくてはいけない。この範囲で関数が定義されているという意味で「定義域」と呼ぶ。定義域は考えている量(物理量だったり測定値だったり)がそもそもどういう量であるかということから決まる場合もあるし、数式の構造から決まる場合もある。たとえば{$\ycol{y}=\sqrt{\xcol{x}}$}という関数は(実数の範囲なら)$\xcol{x}\geq 0$でないと意味がないから、定義域は(もっとも広い場合でも)$\xcol{x}\geq0$である。
$\xcol{x}$が定義域の全体を変化する間に$\ycol{y}$の取り得る値の範囲を「値域(range of values)」と呼ぶ。たとえば上の例$\ycol{y}=\sqrt{\xcol{x}}$の場合、値域は$\ycol{y}\geq0$である。
 のこと? これは関数だけど。
のこと? これは関数だけど。 です。
です。 も、$\xcol{x}=0$の点では対応する$\ycol{y}$がない(定義されてない)から、そこ以外では関数という、制限付きの関数です。
も、$\xcol{x}=0$の点では対応する$\ycol{y}$がない(定義されてない)から、そこ以外では関数という、制限付きの関数です。 を動かしてxを変化させると、それに応じて
を動かしてxを変化させると、それに応じて つまりyが動く。yの方は動かせない。「従属」変数だから。
つまりyが動く。yの方は動かせない。「従属」変数だから。 に近づき、$n$が奇数のとき
に近づき、$n$が奇数のとき に近づく。
に近づく。