積分

$\def\coldr{\rcol{\mathrm dr}}\def\coldvecx{\xcol{\mathrm d\vec x}}\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{~~~~~~~{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}\def\kidy{\opcol{\diff y}}\def\ve{\vec{\mathbf e}}\def\colvecx{\xcol{\vec x}}\definecolor{usuopcolor}{RGB}{237,234,203}\def\usuopcol#1{\color{usuopcolor}#1}\def\vgrad#1{{\usuopcol{\overrightarrow{\opcol{\rm grad}~\kuro{#1}}}}}\def\dX{\rcol{\mathrm dX}}\def\dY{\thetacol{\mathrm dY}}\def\opdf{\opcol{\mathrm df}}\def\coldf{\tcol{\mathrm df}}\def\dtwof{\opcol{\mathrm d^2f}}\def\murasakidb{\zcol{\mathrm d b}}$

　まず、のアプリで積分とはなんぞや、というところをグラフで説明した。

　あとは細かい計算の話。

無限小部分の和としての積分

グラフの面積：直線の例

　アプリでも考えた直角三角形の例をやろう。

　一般的な分割数$N$で作った階段状の図形を次の図のように考えよう（後で$N\to\infty$とする）。

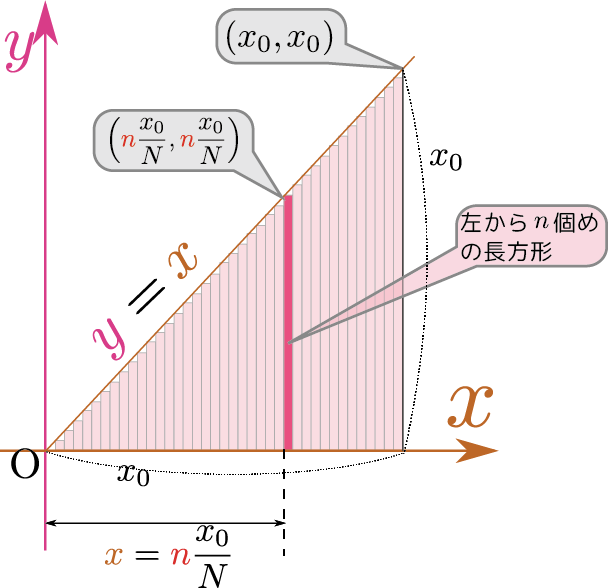
　三角形が横幅${x_0\over N}$の長方形の和で表現されている（長方形の和は、三角形より少しだけ小さい）。一番左の領域を「0番め」と数えて$\ncol{n}$番めの領域（右図で色を濃くした部分）の左端は$\xcol{x}=\ncol{n}{x_0\over N}$であり、その場所の「高さ」も$\ncol{n}{x_0\over N}$である（三角形の斜辺は$\ycol{y}=\xcol{x}$で表されている）。よって、この台形$\ncol{n}=0$のみ、台形ではなく三角形。の形をした領域「台形とわかっているなら台形の面積の公式を使え」と思うかもしれないが、今「三角形」という単純な例を示しているからそうなるのであって、もっと複雑な図形では台形ではない。ここではまず「考えている図形より小さいことが保証される面積」を考えている。にぴたりと収まる長方形の面積は$\ncol{n}{(x_0)^2\over N^2}$である。これを \begin{equation} \sum_{\ncol{n}=0}^{N-1}\ncol{n}{(x_0)^2\over N^2} ={(x_0)^2\over N^2} \sum_{\ncol{n}=1}^{N-1}\ncol{n} =(x_0)^2\times{N-1\over 2N} \end{equation} のように$\ncol{n}=0$から$\ncol{n}=N-1$まで足す実は$\ncol{n}=0$の項は0なので、$\ncol{n}=1$から足しても同じこと。。ここで$\sum_{\ncol{n}=0}^{N-1}\ncol{n}={N(N-1)\over 2}$という和の公式を用いた。最後にある${N-1\over 2N}={1\over 2}-{1\over 2N}$という量は${1\over 2}$より${1\over 2N}$だけ小さい数だから、$N$をどんどん大きくしていけばこの部分が${1\over 2}$となり、長方形の集合の面積は${(x_0)^2\over 2}$、つまり${(底辺)\times(高さ)\over 2}$に下から近づいていく「より小さい」という大小関係を守りつつその値に近づいていく場合は「下から近づく」と表現する。逆の場合は「上から近づく」である。。これで長方形の集合の面積$\leq{(底辺)\times(高さ)\over 2}$が証明正確には、$\leq$ではなく$<$が証明されている。そして、$N\to\infty$においてこれが$=$になるだろう、というのは今の段階だはまだ単なる「予想」でしかない。できた（まだ等式ではない）。

　「隙間にある三角形の分だけ面積は小さくなりませんか？」と気になる人は、アプリの最後のページにもあったように、長方形の作り方を少し変えてみるとよい。

　以下で、もっと一般的な関数（「一般的なグラフ」と言ってもいいし、「一般的な図形」と言ってもいいだろう）に対して同様の計算を行っていく。そこで少し記号を整理しよう。上で考えた${x_0\over N}$という微小長方形の横幅は「$\xcol{x}$の変化量で、後で0になる極限を取るもの」という意味を持っているから、微分の時と同様に、$\coldx$と書くことにしよう同じ意味を持つ量なので、同じ記号を使っている。積分で$\coldx$のような記号が登場するのは、意味のあることである。。$\xcol{x}=\ncol{n}{x_0\over N}$であることも使うと、三角形の面積は（面積が小さくなるように考えた場合） \begin{equation} \sum_{\ncol{n}=1}^N \underbrace{\ncol{n}{x_0\over N}}_{\xcol{x}}\times \underbrace{{x_0\over N}}_{\coldx}=\sum_{\ncol{n}=1}^N\xcol{x}{\coldx} \end{equation} と書くことができる。

　$\xcol{x}\coldx$という部分は、「底辺$\coldx$、高さ$\xcol{x}$」の微小長方形（右の図）の面積を意味しているこの$\coldx$は「$\xcol{x}$で積分しますよ」ということを伝えるためだけにある記号ではなく、積分が「関数の値（今の場合$\xcol{x}$）と微小変化（今の場合$\coldx$）の積を足す」という計算であることから来ている。。

　$N\to\infty$という極限は$\coldx\to0$という極限であり、その極限において今考えている和は「無限個の区間の足算」に変わる。

　$1$から$N$まで$\ncol{n}$を変化させつつ足すが$N\to\infty$（$\coldx\to0$）という極限を取ることによって、$0$から$x_0$まで$\xcol{x}$を変化させつつ足すに変わったのだから、記号の方も$\sum_{\ncol{n}=1}^N$ではない別の記号$\int$の読み方は「いんてぐらる」。記号自体は「積分記号」と呼ぶ。元々は「和」に対応するラテン語（summa、英語のsummation）のsを伸ばして作られた（ライプニッツによる）。$\int_0^{x_0}$を使うことにする。

　こうして新しい記号で書いた$\int_0^{x_0} \xcol{x}\coldx$が「定積分（definite integral）」という演算である（後で「不定積分」も出てくる）。この書き方では結果を \begin{equation} \int_0^{x_0}\xcol{x}\coldx={(x_0)^2\over 2} \end{equation} と表すことができる。

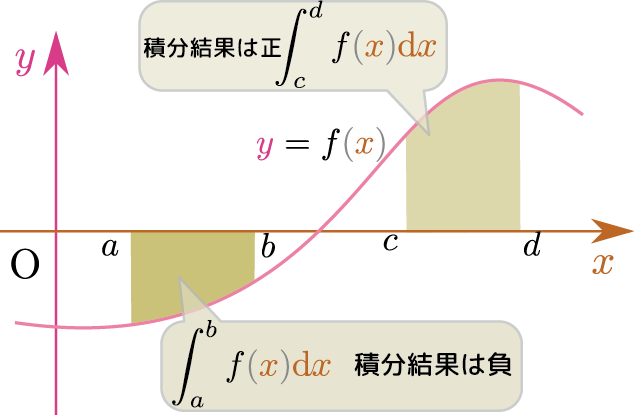
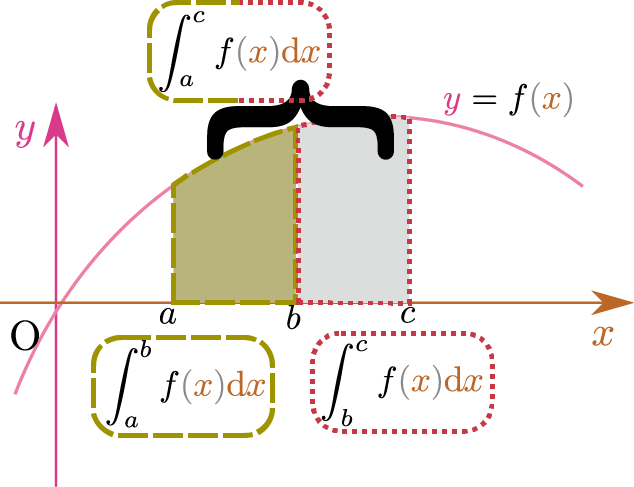
　$\int_a^b$と書いた時の$a$は「（定積分の）下限」、$b$は「（定積分の）上限」と呼び「どこからどこまでを足したのか」を示す$\left(\int_{下限}^{上限}\right)$。領域$a < \xcol{x} < b$は「積分区間」と呼ぶ。上の例では$0,x_0$が下限と上限だったが、もちろんどこからどこまでを足すかは状況によって変わる。

定積分の記号についての整理

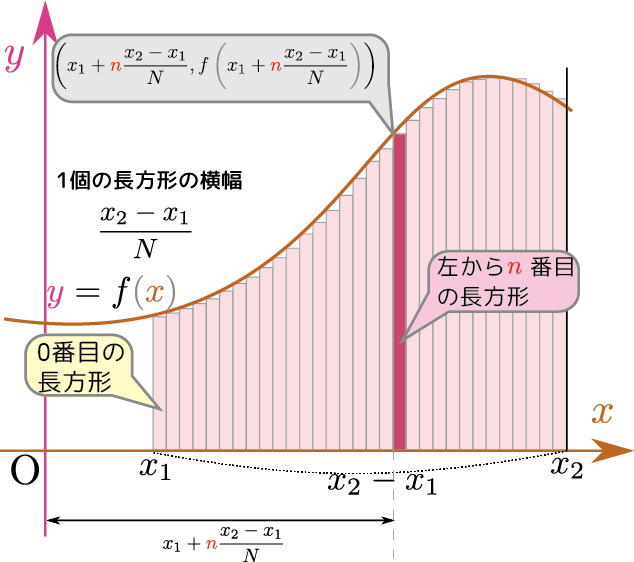
　定積分はもちろん、いろんな関数について実行できる。「$f\kakko{\xcol{x}}$という関数を$x_1$から$x_2$まで定積分する（つまりその範囲で$\xcol{x}$軸とグラフに挟まれた面積を計算する）」を式では$\int_{x_1}^{x_2} f\kakko{\xcol{x}}\coldx$と書く。$f\kakko{\xcol{x}}$は「被積分関数（integrand）」と呼ぶ。また、この時の変数は「積分変数」と呼ぶ。

具体的には「$x_1$から$x_2$まで」という長さ$x_2-x_1$の領域を$N$分割しこの分割の方法は、極限をうまく取ることができるような分割でありさえすればよく、${x_2-x_1\over N}$ごとに等分割する方法が唯一ではない。ここでは一番単純な分割方法で説明している。、その一個一個の微小領域（最初を「0番め」として、$\ncol{n}$番めの微小領域は$\xcol{x}=x_1+\ncol{n}{x_2-x_1\over N}$で始まる）に横${x_2-x_1\over N}$で縦$f\kakko{x_1+ \ncol{n}{x_2-x_1\over N}}$の微小長方形を作り、その面積の和を計算する。式で表現すれば \begin{equation} % \int_{x_1}^{x_2} f\kakko{\xcol{x}}\coldx = \underbrace{\lim_{N\to\infty}\sum_{\ncol{n}=0}^{N-1} }_{\displaystyle \int_{x_1}^{x_2}} \underbrace{f\kakko{x_1 + \ncol{n}{x_2-x_1\over N}}}_{\displaystyle f\kakko{\xcol{x}}}\underbrace{{x_2-x_1\over N}}_{\coldx} \end{equation} である。正確には、上に書いたような単純な極限ではなく、「下からの極限」と「上からの極限」になるようにしてから両方を計算した上で二つの極限が一致することを示さなくてはいけない。一致しない場合は「積分可能でない」関数だったということになる。

この定義からわかるように、$f\kakko{\xcol{x}}$が負の領域での積分はマイナスの値になる。つまり定積分の結果は単純に面積ではなくグラフの線が$\xcol{x}$軸より下にあれば負にして計算する、「符号付き面積」である。「いやそれは困る。面積は正であって欲しい」という人は、絶対値記号を使って$\int \left|f\kakko{\xcol{x}}\right|\coldx$を計算すればよい（実際の計算においては$f\kakko{\xcol{x}}$の正負に応じて場合分けが必要になるだろう）。

定積分の意味するところからわかるように、 \begin{equation} \int_a^b f\kakko{\xcol{x}}\coldx + \int_b^c f\kakko{\xcol{x}}\coldx = \int_a^c f\kakko{\xcol{x}}\coldx\label{intsum} \end{equation} という式が成立するここで、$\xcol{x}=b$で二回同じものを足してはいないかと心配する人がいるかもしれないが、重なりはせいぜい$\Odr\kakko{\Delta x}$の量だから結果には関係ない。。また、 \begin{equation} \int_a^b f\kakko{\xcol{x}}\coldx =- \int_b^a f\kakko{\xcol{x}}\coldx \label{hantaiint} \end{equation} すなわち、「上限と下限を取り替えると符号が変わる」という性質元々の「面積を計算したい」という動機だけから考えると、$a < b$の時に$\int_b^a f\kakko{\xcol{x}}\coldx$を考えるのはナンセンスに思えるかもしれない。しかし、数式を書く上での規則は、できる限り「例外がない」ものが望ましいので、イレギュラーに見える式も作っておけば後で役立つ（かもしれない）。も持つ。この式はどのような$a,b,c$でも成立する式であるべきだこれも「できる限り例外がない規則」が欲しいからである。から、$c=a$を代入すれば右辺が$\int_a^a f\kakko{\xcol{x}}\coldx=0$になることから上の式が導ける。これらを合わせて \begin{equation} \int_a^c f\kakko{\xcol{x}}\coldx - \int_a^b f\kakko{\xcol{x}}\coldx = \int_b^c f\kakko{\xcol{x}}\coldx\label{hikisanint} \end{equation} という式を作ることもできる（上の図をもう一度よく見るとわかる）。この式を使うと、 \begin{equation} \int_{x_1}^{x_2}\xcol{x}\coldx = \int_{0}^{x_2}\xcol{x} \coldx - \int_{0}^{x_1}\xcol{x} \coldx ={(x_2)^2\over 2}-{(x_1)^2\over 2} \end{equation} のようにすることで$\int_{0}^{x_1}\xcol{x} \coldx$の式から$\int_{x_1}^{x_2}\xcol{x}\coldx$が計算できる。一般的には、任意の$x_1$に対し$\int^{x_1}_0f\kakko{\xcol{x}}\coldx$がわかれば任意の範囲での$f\kakko{\xcol{x}}$の定積分を計算することができる。また、微分同様、定積分も線形性を持つ。すなわち以下が成立する。

定積分の線形性

\begin{equation} \int_a^b\left( \alpha f\kakko{\xcol{x}}+\beta g\kakko{\xcol{x}} \right)\coldx =\alpha\int_a^b f\kakko{\xcol{x}}\coldx+\beta\int_a^b g\kakko{\xcol{x}}\coldx \end{equation} ただし、$\alpha,\beta$は任意の定数、$f\kakko{\xcol{x}},g\kakko{\xcol{x}}$を任意のこの範囲で積分可能な関数とする。

　$\coldx$の位置は$\int_a^bf\kakko{\xcol{x}}\coldx$のように後でもいいし、$\int_a^b\coldx f\kakko{\xcol{x}}$のように積分記号の直後でもよい。意味は変わらない（微小長方形の面積を$(縦)\times(横)$と書いても$(横)\times(縦)$と書いても問題ないのと同じ）。

　次に、放物線（ $\ycol{y}=\xcol{x}^2$のグラフ）の下の面積を計算してみよう。同様に$0 < \xcol{x} < x_0$という範囲を考えることにして、その領域を$N$分割して、微小長さ$\coldx={x_0\over N}$ごとに分けて、その微小長さを横、高さを$\ycol{y}=\xcol{x}^2$として作られる長方形の面積をどんどん足していくことにする。

右の図に示したように、$\ncol{n}$番めの長方形の縦の長さは$\left(\ncol{n}\times{x_0\over N}\right)^2$で横が${x_0\over N}$だから、この二つを掛けた答えである$\ncol{n}^2{(x_0)^3\over N^3}$を$\ncol{n}=1$から$\ncol{n}=N-1$ まで足すという計算を行う。結果は \begin{equation} \begin{array}{rl} \sum_{\ncol{n}=1}^{N-1}\ncol{n}^2{(x_0)^3\over N^3} =&{(x_0)^3\over N^3}\underbrace{\sum_{\ncol{n}=1}^{N-1}\ncol{n}^2}_{{N(N-1)(2N-1)\over 6}}\\ =&(x_0)^3\times{(N-1)(2N-1)\over 6N^2} \end{array}\label{NNNN} \end{equation} となる。途中で$\sum_{\ncol{n}=1}^{N-1}\ncol{n}^2={N(N-1)(2N-1)\over 6}$という公式を使っている。最後にある${(N-1)(2N-1)\over 6N^2}$は${\left(1-{1\over N}\right)\left(2-{1\over N}\right)\over 6}$と書き直せるから、$N\to\infty$で${1\over 3}$に収束する。よって、今考えている面積は${(x_0)^3\over 3}$へと収束する。前節同様、今求めた面積（「下からの極限」）は求めたい面積より少し小さいが、今求めた面積より少し大きい「上からの極限」がやはり${(x_0)^3\over 3}$へ収束することがわかるので、 \begin{equation} \int_0^{x_0}\xcol{x}^2\coldx={(x_0)^3\over 3}\label{sekibunxsq} \end{equation} が求められる。ここで求めたのは「$0$から$x_0$まで」だが、ここまでやっておけば、任意の範囲についての積分は以下のように計算できる。 \begin{equation} \int_{x_1}^{x_2}\xcol{x}^2\coldx = \int^{x_2}_{0}\xcol{x}^2\coldx - \int^{x_1}_{0}\xcol{x}^2\coldx={(x_2)^3\over 3}-{(x_1)^3\over 3} \end{equation} 「では次に$\xcol{x}^3$を考えよう」と行きたいところだが、この方法はいずれ行き詰まる。というのは、$\sum_{\ncol{n}=1}^{N-1}\ncol{n}={N(N-1)\over 2}$や$\sum_{\ncol{n}=1}^{N-1}\ncol{n}^2={N(N-1)(2N-1)\over 6}$の次の公式$\sum_{\ncol{n}=1}^{N-1}\ncol{n}^3={N^2(N-1)^2\over 4}$あたりからは知らない人も多いだろうそういう時は公式集を持ってくればよい。たくさんの公式を全部覚えておく必要などない。ただ「こういう公式がある」を知らないと公式集を引くこともできないから、いろいろな式があることを知っておくべきなのはもちろんのことである。。それに$x^{1.3}$のような整数べきでない場合はもっと難しそうだ。

　一般の$\alpha$の場合の$\xcol{x}^\alpha$の積分は、等分割でない分割を使う方法あるし、次の節で考える微積分学の基本定理を使う方法もある。

微積分学の基本定理と不定積分

ここまでの計算でわかった、

　定積分における$\xcol{x}^\alpha\to {(x_0)^{\alpha+1}\over \alpha+1}$

という対応関係と、

　微分における$\xcol{x}^\alpha \to \alpha \xcol{x}^{\alpha-1}$（あるいは、この$\alpha$を一つずらした$\xcol{x}^{\alpha+1}\to (\alpha+1)\xcol{x}^\alpha$）

という対応関係を比較してみよう。

　この二つが「逆」であることに気づいたろうか（冪が$\alpha\to\alpha+1$と上がるか$\alpha+1\to\alpha$と下がるか、係数は$\alpha+1$を掛けるか、$\alpha+1$で割るか）。そのつながりこそが「微積分学の基本定理」の一つの顕れである。

微分積分学の基本定理

えらく大層な名前だが、実は単純なことで、一文で表すならば「積分の逆の演算が微分である」に過ぎない。説明の前にもう一度確認しておくが、定積分$\int_a^b f\kakko{\xcol{x}}\coldx$という量は、関数$f\kakko{\xcol{x}}$と、下限$a$と上限$b$のすべてに依存する。とりあえず関数$f\kakko{\xcol{x}}$の形と下限$a$は「変化しない」としておくと、定積分$\int_a^b f\kakko{\xcol{x}}\coldx$は上限$b$の関数であると考えてもよい。つまり、 \begin{equation} F\kakko{\zcol{b}}=\int_a^{\zcol{b}}f\kakko{\xcol{x}}\coldx \end{equation} のような関数$F\kakko{\zcol{b}}$（この式から、$\zcol{b}$は変数として扱うので色をつける。本書では「変化させることができるもの」を色付きで表すが、どれが「変化させることができる」かは文脈で決まる）を考える実際にはこの量は$a$にもよるし、関数$f$の形にもよるので、$F_f\kakko{a,b}$とでも書くべきであろうが、ここでは$a$は変化しない定数だとして扱っているので略している。。この$F\kakko{\zcol{b}}$は後で定義する「原始関数」の一例である原始関数には、元の関数の名前を大文字に変えた記号を使う事が多い（$f\kakko{\xcol{x}}$の原始関数は$F\kakko{\xcol{x}}$のように）。ただし、そうでない場合もあるので注意。。ここで、$\zcol{b}$の変化による$F\kakko{\zcol{b}}$の変化の割合（微分）を考えると、

微積分学の基本定理の一つの表現

　$F\kakko{\zcol{b}}=\int_a^{\zcol{b}} f\kakko{\xcol{x}}\coldx$を$\zcol{b}$で微分すると、$\opcol{{\diff \over \kidb}}\left(\int_a^{\zcol{b}} f\kakko{\xcol{x}}\coldx\right)=f\kakko{\zcol{b}}$となり、元の関数に戻る（ただし、変数は$\zcol{b}$に変わる）。

が成り立つことが、ここまでやった定積分という計算の意味をわかっていればわかると思う。図でその意味を確認しておこう。

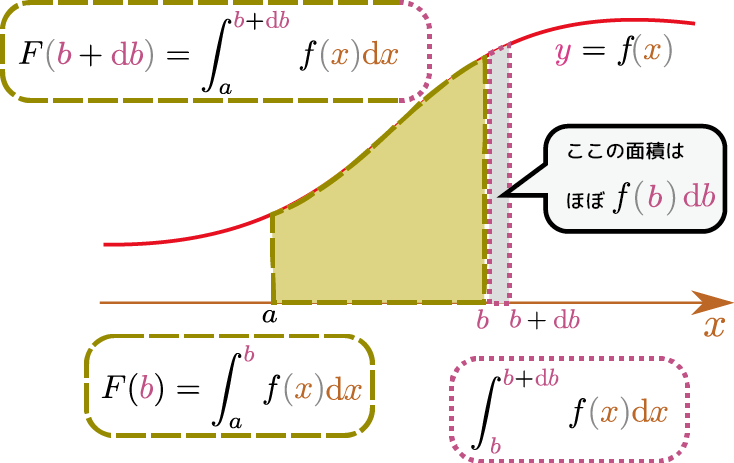
　積分の上限$\zcol{b}$を少し変化させる。積分の結果である面積は図に示したの分だけ増加する。この部分を例によって「幅$\murasakidb$、高さ$f\kakko{\zcol{b}}$の長方形」と考える（右下の図に書いた三角形に近い形の部分を無視する）と、$F\kakko{\zcol{b}}$の変化量は$f\kakko{\zcol{b}}\murasakidb$である（厳密には後に$\Odr\kakko{\murasakidb^2}$がつく）。これで \begin{equation} F\kakko{\zcol{b}+\murasakidb}=F\kakko{\zcol{b}}+f\kakko{\zcol{b}}\murasakidb \end{equation} が示せた。

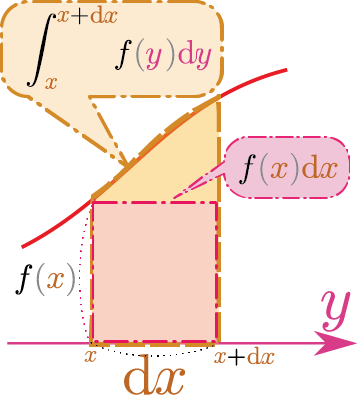
　一般的な微分の式$g\kakko{\xcol{x}+\coldx}=g\kakko{\xcol{x}}+g'\kakko{\xcol{x}}\coldx$と上の$f$と混同しないように$g$を用いたが、式の意味は変わらない。見比べる（$F\to g,f\to g'$という対応になっていることに注意）ことにより、$F\kakko{\zcol{b}}$の微分が$f\kakko{\zcol{b}}$だということ（$F'\kakko{\zcol{b}}=f\kakko{\zcol{b}}$）がわかる。これで微積分学の基本定理が示せた。

　微分積分学の基本定理のありがたみは、どちらかというと面倒な計算である「積分」を「微分の逆」という形で計算できることである。たとえば我々は$\ddx \left(\xcol{x}^\alpha\right)=\alpha \xcol{x}^{\alpha-1}$をすでに知っているので、 \begin{equation} \ddx \left(\xcol{x}^\alpha\right)=\alpha \xcol{x}^{\alpha-1}~~の逆として~~ \int_a^b \alpha\xcol{x}^{\alpha-1} \coldx =b^\alpha - a^\alpha \end{equation} を得る。あるいは、$\alpha=\beta+1$として両辺を$\alpha$で割って、 \begin{equation} \int_a^b \xcol{x}^{\beta} \coldx ={b^{\beta+1}\over \beta+1} - {a^{\beta+1}\over \beta+1}\label{teisekibunxalpha} \end{equation} という式を作ることができる。以下でもこれを使って計算しにくい積分を求めていく。

原始関数と不定積分

　前節で使った記号$F\kakko{\xcol{x}}$は、「定積分の結果を上限の関数として表したもの」であったが、結局それは「微分したら積分する前の関数に戻るもの」でもあった。そこでより一般的に「原始関数（primitive function）」という関数$F\kakko{\xcol{x}}$を、

原始関数の定義

\begin{equation} 微分するとf\kakko{\xcol{x}}になる、すなわち f\kakko{\xcol{x}}=\ddx F\kakko{\xcol{x}}となる関数F\kakko{\xcol{x}}\label{gensikansuudef} \end{equation}

で定義する原始関数を表現する時には、大文字（$f$に対して$F$など）を使うことが多い。（「原始」という言葉はもちろん「微分する前」ということ）。ただし、「定積分の結果を上限の関数として表したもの」は原始関数になるが、原始関数は常に「定積分の結果を上限の関数として表したもの」になるとは限らない。

　ある原始関数$F\kakko{\xcol{x}}$が求められたとすると、それに任意の定数を足したもの$F\kakko{\xcol{x}}+C$も、 \begin{equation} \ddx \left(F\kakko{\xcol{x}}+C\right) =\ddx F\kakko{\xcol{x}}+\underbrace{\ddx C}_{0} =f\kakko{\xcol{x}} \end{equation} となり$f\kakko{\xcol{x}}$の原始関数たる条件「微分したら$f\kakko{\xcol{x}}$になる」を満たす。ゆえに原始関数は一つに決まらないが、原始関数の定義が必然的にそうなるようにできているのだから仕方がない。そもそも微分という演算が「定数を消してしまう」演算なので、「微分の逆」を考えた時に定数の分だけ決まらないのは当然である。

　原始関数がわかれば、定積分は \begin{equation} \int_{x_1}^{x_2}f\kakko{\xcol{x}}\coldx = F\kakko{x_2}-F\kakko{x_1}=\bigl[F\kakko{\xcol{x}}\bigr]_{x_1}^{x_2}\label{teisekibungensi} \end{equation} のように上限での原始関数の値$-$下限での原始関数の値で計算できる。この量を（上の式の最後でも書いたように）$\bigl[F\kakko{\xcol{x}}\bigr]_{x_1}^{x_2}$すなわち、$\left[原始関数\kakko{\xcol{x}}\right]_{{}_{下限}}^{{}_{上限}}$という記号を使って書く。この式においても、原始関数$F\kakko{\xcol{x}}$の「定数$C$を足してもやはり原始関数である」という性質は変わらない。 \begin{equation} \int_{x_1}^{x_2}f\kakko{\xcol{x}}\coldx = \bigl[F\kakko{\xcol{x}}+C\bigr]_{x_1}^{x_2} =F\kakko{x_2}+C-\left(F\kakko{x_1}+C\right)=F\kakko{x_2}-F\kakko{x_1}\label{kieruteisuu} \end{equation} となって定積分の結果に$C$は影響しない。

　ここまでで考えた例では、$\xcol{x}^\alpha$の原始関数（の一つ）が${\xcol{x}^{\alpha+1}\over \alpha+1}$である。式を見ると、 \begin{equation} \int_a^b \xcol{x}^{\beta} \coldx =\left[{\xcol{x}^{\beta+1}\over \beta+1}\right]_a^b ={b^{\beta+1}\over \beta+1} - {a^{\beta+1}\over \beta+1} \end{equation} と書けることがわかるが、実際、 \begin{equation} \ddx \left(\xcol{x}^{\alpha+1}\right)=(\alpha+1)\xcol{x}^{\alpha} \end{equation} となっている。

　$c$を下限とした定積分$\int_c^{\xcol{x}}f\kakko{\ycol{y}}\coldy=F\kakko{\xcol{x}}-F\kakko{c}$は原始関数の一つである。$f\kakko{\ycol{y}}=\ycol{y}$の場合、原始関数の一つは \begin{equation} F\kakko{\xcol{x}}=\int_c^{\xcol{x}}\ycol{y}\coldy=\left[{\ycol{y}^2\over 2}\right]_c^{\xcol{x}} ={\xcol{x}^2\over 2}-{c^2\over 2} \end{equation} になる（当たり前だが微分すると$\xcol{x}$に戻る）。$c$がなんでもよいので、最後についている$-{c^2\over 2}$の分だけ、原始関数$F\kakko{\xcol{x}}$は不定性を持つ。これは上の$C$が任意であったことの反映である実は$-{c^2\over 2}$は常に0以下だが、$C$は正の数であってもよい（任意）から、$C$の方が範囲が広い。原始関数が必ずしも「定積分の結果の上限の関数」という形にならないと書いたのはこういう例があるからである。。

　関数$f\kakko{\xcol{x}}$から原始関数$F\kakko{\xcol{x}}$を求める演算を「不定積分（indefinite integral）」と呼ぶ。

　不定積分の記号は、定積分の記号から（不定積分では不要である）積分範囲を外して、

不定積分

\begin{equation} \begin{array}{c} \ddx F\kakko{\xcol{x}}=f\kakko{\xcol{x}}であるとき、\\[3mm] \intdx f\kakko{\xcol{x}}= F\kakko{\xcol{x}}~~~または\int f\kakko{\xcol{x}}\dx=F\kakko{\xcol{x}} \end{array} \end{equation}

のように書く。不定積分の答え$F\kakko{\xcol{x}}$には上に述べた定数$C$の分だけの「不定性」がある（こうなるから「\強調{不定}積分」だと覚えておくとよい）。

　定積分の記号を流用して同じような形の式に書いているが、不定積分という操作は「関数$f\kakko{\xcol{x}}$から原始関数$F\kakko{\xcol{x}}$へ」という対応関係微分の「関数$f\kakko{\xcol{x}}$から導関数$f'\kakko{\xcol{x}}$へ」という対応関係の逆である。であり、一方の定積分は「関数$f\kakko{\xcol{x}}$と領域（下限〜上限）から、積分結果という一つの数へ」定積分の方は積分の上限・下限を決めて$\int_a^b f\kakko{\xcol{x}}\coldx$と書いた時点で値は一つに決っている。という対応関係であるだからむしろ不定積分の記号は「微分の逆」という意味で$\opcol{\left({\diff \over \kidx }\right)^{-1}}$のように書くべきかもしれないが、普通この記法は使われない。「微分演算子の逆の演算子」というのは実際に微分方程式を解くときの技法としては使われることもある。。

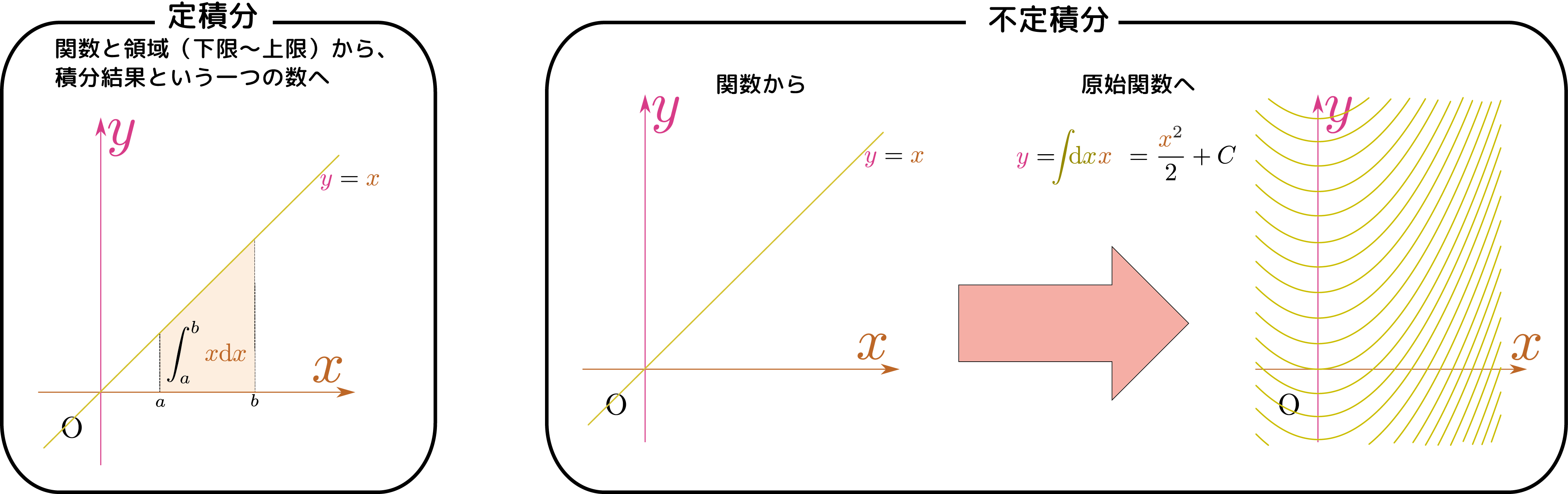
　ちょうど、微分を「微分演算子$\ddx$を掛ける」ことで表現したように、不定積分という演算は「前から`積分演算子'$\opcol{\int\!\!\kidx}$を掛ける」$\int f\kakko{\xcol{x}}\dx $という書き方の時は「前から$\int$を、後ろから$\dx$を掛ける」になる。という演算だとして表現できる。定積分の$\coldx$は「微小な変化量」という意味が明確だったが、それに比べると不定積分の$\kidx$はむしろ「積分という演算を表現する記号$\opcol{\int\!\! \kidx}$」の一部であると言える。

　不定積分は名前の通り、定数を付加できる分だけ決まらない。だから、 \begin{equation} \intdx\xcol{x} = {\xcol{x}^2\over 2}+C \end{equation} のように「まだ決まってない定数（上の式の場合$C$）」をつけて結果を示す。これを「積分定数（constant of integration）」と呼ぶ（文字はよく$C$を使うがそうでなくてはいけないわけではない）。積分定数は不定積分の時は必要だが、定積分の時はどうせ消えてしまう運命にあるので、定積分の括弧$\left[~~~~~~\right]$の内側に積分定数をつける必要はない（つけたければつけてもよいが）。

　不定積分は「微分の逆」であるとよく言われる。しかし、 \begin{equation} \ddx \intdx f\kakko{\xcol{x}}=f\kakko{\xcol{x}}\label{motonimodoruyo} \end{equation} のように「不定積分してから微分」は元に戻るが、逆の「微分してから不定積分」の結果は \begin{equation} \intdx \ddx f\kakko{\xcol{x}}=f\kakko{\xcol{x}}+C\label{motonimodoru} \end{equation} のように元に戻らず、積分定数$C$の分だけ不定となることに注意しよう。