積分(続き)
その他、いろんな関数の積分
${1\over \xcol{x}}$の積分
$\xcol{x}^\alpha$の不定積分は$\intdx \xcol{x}^\alpha = {\xcol{x}^{\alpha+1}\over \alpha+1}+C$は$\alpha\neq -1$のときに正しい式であった。$\alpha=-1$の時、つまり、$\intdx {1\over \xcol{x}}$はまだ求められていない。しかしすでに「微積分学の基本定理」を知っているので微分して${1\over \xcol{x}}$になるものを探せばよい。$\ddx \log \xcol{x}={1\over \xcol{x}}$であるから、以下がわかる。
${1\over\xcol{x}}$の不定積分
\begin{equation} \intdx {1\over \xcol{x}} = \log\xcol{x}+C\label{intoneoverx} \end{equation}
ここで注意しておいて欲しいのは、$\xcol{x}$が負の場合。この点を気にして右辺を$\log|\xcol{x}|+C$のように絶対値をつけて表現することもある。しかしオイラーの関係式から示されるように、$\E^{\mathrm i\pi}=-1$なので$\log\kakko{-1}=\mathrm i\pi$と考えれば、$\xcol{x}$が負の時は$\xcol{x}=-|\xcol{x}|$とすれば、 \begin{equation} \log \xcol{x}= \log\kakko{-|\xcol{x}|}=\log|\xcol{x}|+ \log\kakko{-1}=\log|\xcol{x}|+\mathrm i\pi\label{logminus} \end{equation} となり、絶対値があるかないかは定数$\mathrm i\pi$がつくかつかないかの差である。この$\mathrm i\pi$も含めて積分定数$C$と思えば、問題ない。「積分定数は実数であって欲しい」と考えるなら、絶対値は必要である。
もう一つ注意しておくと、${1\over \xcol{x}}$は$\xcol{x}=0$で不連続である($\xcol{x}>0$と$\xcol{x}<0$の関数はつながっていない)。よって積分結果も正の領域と負の領域では別物である。したがって不定積分は厳密には、 \begin{equation} \intdx {1\over \xcol{x}} = \begin{cases} \log\xcol{x}+C_1& \xcol{x}<0のとき\\ \log\xcol{x}+C_2& \xcol{x}>0のとき \end{cases} \end{equation} のように領域により別の積分定数をもってよい(微分すればどちらも${1\over \xcol{x}}$に戻る)。これは他の不連続な点を持つ関数でも同様である。以上のように、不連続点をまたぐ範囲の定積分には注意が必要である。
これは$\E^{\mathrm i\pi}=-1$だから成り立つ式…なのだが一つ落とし穴があって、$\E^{-\mathrm i\pi}$も$\E^{3\mathrm i\pi}$も$-1$(実際のところ、$n$を任意の整数として、$\E^{(2n+1)\mathrm i\pi}=-1$)であるから、$\log\kakko{-1}=-\I\pi$または$\log\kakko{-1}=3\mathrm i\pi$としてもよい(一般的には、$n$を任意の整数として$\log\kakko{-1}=(2n+1)\I\pi$)。たいていの場合、たくさんの値の代表として$\log\kakko{-1}=\mathrm i\pi$を選ぶ。
三角関数の積分
三角関数の微分はすでに求めてあるので、「微積分学の基本定理」を使えば積分も簡単と言えば簡単なのだが、ここではあえて「足算の化け物」としての「三角関数の定積分」を求めよう。
たとえば$\int_0^{\theta_0} \cos \thetacol{\theta}\coldtheta$はどんな量になるだろうか。
「グラフを描いて面積を〜」と言われてもどうしていいのかわからないかもしれない。そこでまず、$\coldtheta\cos \thetacol{\theta}$という「長さ」を図に描いてみる。
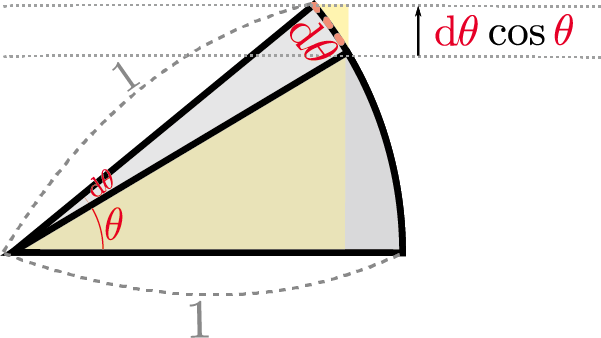
上の図にあるように、斜辺が1の直角三角形の角度を$\thetacol{\theta}\to\thetacol{\theta}+\coldtheta$と変化させた時の「直角三角形の高さの変化」が$\coldtheta\cos \thetacol{\theta}$である。

これを逆に足していくと考えると、$\thetacol{\theta}=0$から$\thetacol{\theta}=\theta_0$まで足せば、その時の直角三角形の高さ$\sin \theta_0$になるだろう、と予想される。これから我々は、 \begin{equation} \int_0^{\theta_0} \cos \thetacol{\theta} \coldtheta = \sin \theta_0 \end{equation} を得る。これは、 \begin{equation} % \int_0^{\theta_0} \cos \thetacol{\theta} \coldtheta = \bigl[\sin \thetacol{\theta}\bigr]_0^{\theta_0} =\sin\theta_0 - \sin 0 =\sin \theta_0 \end{equation} と考えることもできる。$\cos\thetacol{\theta}$の原始関数が$\sin\thetacol{\theta}$だったこと(逆に$\ddtheta\sin \thetacol{\theta}=\cos\thetacol{\theta}$だったこと)を思い出せば、この結果はもっともである。
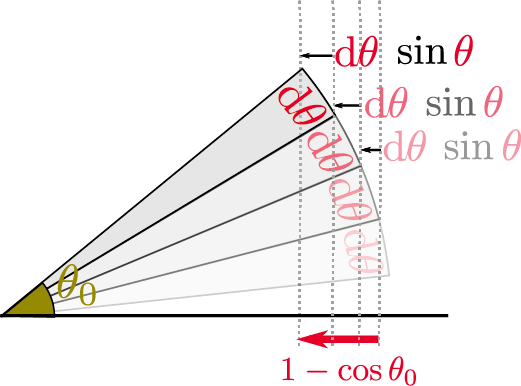
のように、「横幅を足していく」という計算をすればよい…のだが難しく考えすぎている人、深く考えずに「$-\cos\theta_0$」などと答えている人もいたが、正の微小長さを足しているのに負になるはずはない。
実際の答えは、図にも書いたように、$\coldtheta \sin \thetacol{\theta}$という量をどんどん足していくと考えて、 \begin{equation} \int_0^{\theta_0} \sin \thetacol{\theta} \coldtheta = 1-\cos \theta_0 \end{equation} を得る。こちらも原始関数を使った形で書こう。$\cos 0=1$であることを考えると、 \begin{equation} \begin{array}{rl} \int_0^{\theta_0} \sin \thetacol{\theta} \coldtheta =& 1-\cos\theta_0 = -\cos\theta_0 - \underbrace{(-\cos 0)}_{-1} \end{array} \end{equation} となり、さらに$-\cos\theta_0 - (-\cos 0)=\left[-\cos \thetacol{\theta}\right]_0^{\theta_0}$のように定積分で使う記号を使って書き直すことができる。つまり$\int_0^{\theta_0} \sin \thetacol{\theta} \coldtheta =\left[-\cos \thetacol{\theta}\right]_0^{\theta_0}$だから、$\sin\thetacol{\theta}$の原始関数は$-\cos\thetacol{\theta}$である($\ddtheta\cos\thetacol{\theta}=-\sin\thetacol{\theta}$すなわち$\ddtheta\left(-\cos\thetacol{\theta}\right)=\sin \thetacol{\theta}$)。
$\tan$は$\sin,\cos $に比べ少しややこしいので、図形ではなく「原始関数を求める」方向で考えよう。$\tan \theta={\sin \theta\over \cos \theta}$という式と、$\log f\kakko{\thetacol{\theta}}$の微分の式を見比べる。 \begin{equation} \ddtheta\left( \log{ f\kakko{\thetacol{\theta}}} \right)={1\over f\kakko{\thetacol{\theta}}}\ddtheta f\kakko{\thetacol{\theta}},~~~~ \tan\thetacol{\theta}={\sin\thetacol{\theta}\over \cos \thetacol{\theta}} =-{1\over \cos\thetacol{\theta}}\ddtheta\left( \cos \thetacol{\theta}\right) \end{equation} 最後で、$\cos \thetacol{\theta}$を微分すると$-\sin \thetacol{\theta}$であることを使った。これを見比べると、 \begin{equation} \ddtheta\left( -\log\kakko{\cos \thetacol{\theta}} \right)={\sin \thetacol{\theta}\over \cos\thetacol{\theta}}=\tan \thetacol{\theta} \end{equation} とわかる。ゆえに、 \begin{equation} \opcol{\int\!\!\!\kidtheta} ~\tan \thetacol{\theta} = -\log\kakko{\cos \thetacol{\theta}}+C~~~(Cは積分定数) \end{equation} である。この$\log\kakko{\cos\thetacol{\theta}}$も絶対値は不要である(つけてもよい)。
指数関数の積分
指数関数(代表例として$\E^{\xcol{x}}$)の積分は簡単である。なぜなら$\E^{\xcol{x}}$は「微分しても変化しない関数」なのだから、積分しても変化しないに決っている。よって、
指数関数の不定積分
\begin{equation} \intdx \E^{\xcol{x}} = \E^{\xcol{x}} +C~~~~(Cは積分定数) \end{equation}
となる。「変わらない」と言ってもこっちには積分定数が付く。そのため「積分の積分」は、 \begin{equation} \intdx\left(\intdx~ \E^{\xcol{x}} \right) = \intdx \left( \E^{\xcol{x}} +C\right) =\E^{\xcol{x}} + C \xcol{x} +D \end{equation} となる。指数関数は何度微分しても指数関数だが、積分の方は違う関数になる。ここで$D$は2個めの積分定数で、1個めの$C$とは別の数であってよい。
対数関数の積分
$\log \xcol{x}$の積分は、直観的には難しい。というのは$\ddx\mbox{なんとか}=\log \xcol{x}$になるなんとかをすぐには思いつけないからである。後で示す部分積分の方法を使うという手もあるのだが、ここでは
間違った予想
$$ \intdx\log \xcol{x} =\xcol{x}\log \xcol{x} $$
から入ろう。不定積分は微分したら元に戻るはずである。では微分してみよう。 \begin{equation} \ddx \left(\xcol{x}\log \xcol{x}\right)=\underbrace{\log \xcol{x} }_{\xcol{x}の方を微分した}+ \underbrace{\xcol{x} \times{1\over \xcol{x}}}_{\log \xcol{x}の方を微分した}=\log \xcol{x} +1 \end{equation} となるから、微分の結果は$\log\xcol{x}$にならない。しかし、左辺の括弧内から$\xcol{x}$で微分すると1になるものを、右辺から1を引けば欲しい式が出てくることがわかる。よって \begin{equation} \ddx \left(\xcol{x}\log \xcol{x}-\xcol{x}\right)=\log \xcol{x} \end{equation} とすればよい。よって以下のように結論できる。
対数関数の不定積分
\begin{equation} \intdx\log \xcol{x} = \xcol{x}\log \xcol{x} -\xcol{x}+C~~~~(Cは積分定数)\label{logintdx} \end{equation}
積分の技法と応用
部分積分
微分のライプニッツ則$\ddx \left(f\kakko{\xcol{x}}g\kakko{\xcol{x}}\right)=\left(\ddx f\kakko{\xcol{x}}\right)g\kakko{\xcol{x}}+f\kakko{\xcol{x}}\ddx g\kakko{\xcol{x}}$の逆を考えるのが「部分積分」である。まず上の式を不定積分し(左辺は微分する前に戻る)、 \begin{equation} \begin{array}{rll} \intdx \ddx \left(f\kakko{\xcol{x}}g\kakko{\xcol{x}}\right) =&\intdx \left(\ddx f\kakko{\xcol{x}}\right)g\kakko{\xcol{x}} +\intdx f\kakko{\xcol{x}}\ddx g\kakko{\xcol{x}}\\[3mm] f\kakko{\xcol{x}}g\kakko{\xcol{x}} =&\underbrace{\intdx \left(\ddx f\kakko{\xcol{x}}\right)g\kakko{\xcol{x}}}_{←移項する} +{\intdx f\kakko{\xcol{x}}\ddx g\kakko{\xcol{x}}}\\ f\kakko{\xcol{x}}g\kakko{\xcol{x}}-\intdx\left( \ddx f\kakko{\xcol{x}}\right)g\kakko{\xcol{x}} =&\intdx f\kakko{\xcol{x}}\ddx g\kakko{\xcol{x}} \end{array} \end{equation} となる1行目から2行目に行く時の左辺の積分で積分定数がないが、右辺にまだ不定積分が残っていてそちらからも積分定数が出てくるので、そちらに吸収させる。。ここで、左右を取り替えて、
部分積分の公式(不定積分)
\begin{equation} \intdx f\kakko{\xcol{x}}\ddx g\kakko{\xcol{x}} =- \intdx \left( \ddx f\kakko{\xcol{x}}\right)g\kakko{\xcol{x}} +f\kakko{\xcol{x}}g\kakko{\xcol{x}}\label{pidint} \end{equation}
という公式ができる。
例として、$\intdx \xcol{x} \cos \xcol{x}$をあげよう。この場合、$\ddx g\kakko{\xcol{x}}=\cos\xcol{x},f\kakko{\xcol{x}}=\xcol{x}$という代入を行っていけば、 \begin{equation} \intdx \underbrace{\xcol{x}}_{f\kakko{\xcol{x}}}\underbrace{\cos \xcol{x}}_{g'\kakko{\xcol{x}}} = - \intdx \underbrace{1}_{f'\kakko{\xcol{x}}}\underbrace{\sin \xcol{x}}_{g\kakko{\xcol{x}}} +\underbrace{\xcol{x}}_{f\kakko{\xcol{x}}}\underbrace{\sin \xcol{x}}_{g\kakko{\xcol{x}}} =\underbrace{\cos \xcol{x}+C}_{\tiny -\intdx \sin \xcol{x}} +\xcol{x}\sin \xcol{x} \end{equation} のようにして積分ができる。
「部分積分」はある意味微分演算子$\ddx$を右から左へ付け替えるという計算でもある。「微分演算子を掛ける」という操作は通常の掛算とは違う。通常の数の掛算なら$a\times (b\times c)=(b\times a)\times c$という「付け替え操作」ができるが、微分演算子の「付替え」には、符号を変えたり最後に「おつり」を付けたりという手順が必要であるこういう手順を踏まなくてはいけないことを単に「押し付けられたルール」と受け取ると「面倒だ」と思うかもしれないが、それは数学の勉強方法として正しくない。ここでやっている計算の意味をちゃんと把握していればこの手順は必然的なものであることがわかる。計算の中身と意義を確認し納得した上で使っていこう。。
同じことなのだが、公式に代入する、という考え方ではなく、 \begin{equation} \begin{array}{rll} & \intdx \xcol{x} \cos \xcol{x} &\kokode{\cos \xcol{x} =\ddx \sin \xcol{x}}\\ =& \intdx \xcol{x} \ddx \sin \xcol{x} &\kokode{ライプニッツ則}\\ =&\intdx \left( \ddx \left(\xcol{x}\sin \xcol{x}\right) -\left( \ddx \xcol{x}\right)\sin \xcol{x} \right)&\kokode{微分の積分は元に戻る、および\ddx \xcol{x}=1}\\ =&\xcol{x}\sin \xcol{x}\underbrace{-\intdx\sin \xcol{x}}_{+\cos\xcol{x}+C}~ \end{array}\end{equation} のように既に知っているライプニッツ則の方だけを使っても計算ができる。
部分積分という計算は積の片方を微分してもう片方を積分するという計算になっているから、$\log$や$\arctan$のように「微分すると簡単になるんだけどなぁ」と言いたくなる関数と簡単に積分できる関数の積が出てきた時は、部分積分が有効ではないかと試してみるとよいだろう。
定積分の場合も同様に計算ができて、
部分積分の公式(定積分)
\begin{equation} \int_a^b f\kakko{\xcol{x}}\ddx g\kakko{\xcol{x}}\coldx =- \int_a^b \left(\ddx f\kakko{\xcol{x}}\right)g\kakko{\xcol{x}}\coldx +\underbrace{\left[ f\kakko{\xcol{x}}g\kakko{\xcol{x}}\right]_a^b}_{表面項} \end{equation}
となる。
最後の部分は$\left[f\kakko{\xcol{x}}g\kakko{\xcol{x}}\right]_a^b=f\kakko{b}g\kakko{b}-f\kakko{a}g\kakko{a}$となって、積分の「表面」である$\xcol{x}=a$と$\xcol{x}=b$\linebreak[3]での値だけになるので、「表面項(surface term)」と呼ばれる表面項は「表面」が問題にならないような場合(たとえば積分範囲が$-\infty<\xcol{x}<\infty$で、無限に遠いところは考えなくてもよいような場合など)は無視される。しかし、無視してはいけない場合も、もちろんある。。
置換積分
置換積分の手順
$\xcol{x}$を独立変数としたある積分$\int f\kakko{\xcol{x}}\coldx$という積分を考える。ここで、$\tcol{t}$という別の変数($\xcol{x}$とは$\xcol{x}=g\kakko{\tcol{t}}$という関係で繋がっている)へと独立変数を変えた時に、積分がどう変わるかを考えてみる。まず、$f\kakko{\xcol{x}}$という関数は$f\kakko{g\kakko{\tcol{t}}}$という$\tcol{t}$の関数へと変えなくてはいけない。と同時に、積分要素も変わるが、この時、$\coldx={\coldx\over\coldt}\coldt$という関係を使って変換するのが置換積分である。具体的にはこうなる。
置換積分の公式
\begin{equation} \int f\kakko{\xcol{x}}\coldx = \int f\kakko{x\kakko{\tcol{t}}}{\coldx\over \coldt}\coldt\label{tikankousiki} \end{equation}
この式は合成関数の微分則(chain rule)の逆をやっていると思えばよい。$f\kakko{\xcol{x}}$の原始関数を$F\kakko{\xcol{x}}$とする。ここでこの$\xcol{x}$は$\tcol{t}$の関数なので、$x\kakko{\tcol{t}}$と書くことにする($F\kakko{x\kakko{\tcol{t}}}$)。この式を$\tcol{t}$で微分すると、 \begin{equation} {\ddt}\left(F\kakko{x\kakko{\tcol{t}}}\right) =\underbrace{\left( \ddx F\kakko{\xcol{x}}\biggr|_{\xcol{x}=x\kakko{\tcol{t}}}\right)}_{f\kakko{x\kakko{\tcol{t}}}}\left( {\ddt}x\kakko{\tcol{t}} \right) \end{equation} であるが、これをもう一回$\tcol{t}$で不定積分すれば、 \begin{equation} F\kakko{x\kakko{\tcol{t}}} =\int f\kakko{x\kakko{\tcol{t}}} \left( {\ddt}x\kakko{\tcol{t}} \right)\coldt \end{equation} となる。
たとえば \begin{equation} \int \xcol{x}\sin \xcol{x}^2\coldx \end{equation} において、$\xcol{x}^2=\tcol{t}$とおくと、$2\xcol{x}\coldx =\coldt$となるから、 \begin{equation} \int \xcol{x}\sin \xcol{x}^2\coldx={1\over 2} \int \sin \tcol{t}\coldt=-{1\over 2}\cos \tcol{t}+C=-{1\over 2}\cos \xcol{x}^2+C \end{equation} と書きなおしてよい(逆に微分すれば元に戻ることは確かめられる)。
置換積分でやっていること
置換積分を使うとできる積分の例として、 \begin{equation} \int_0^1 \sqrt{1-\xcol{x}^2}\coldx = {\pi\over 4} \end{equation} を取り上げる。この計算がどのような意味を持つかグラフに示した。
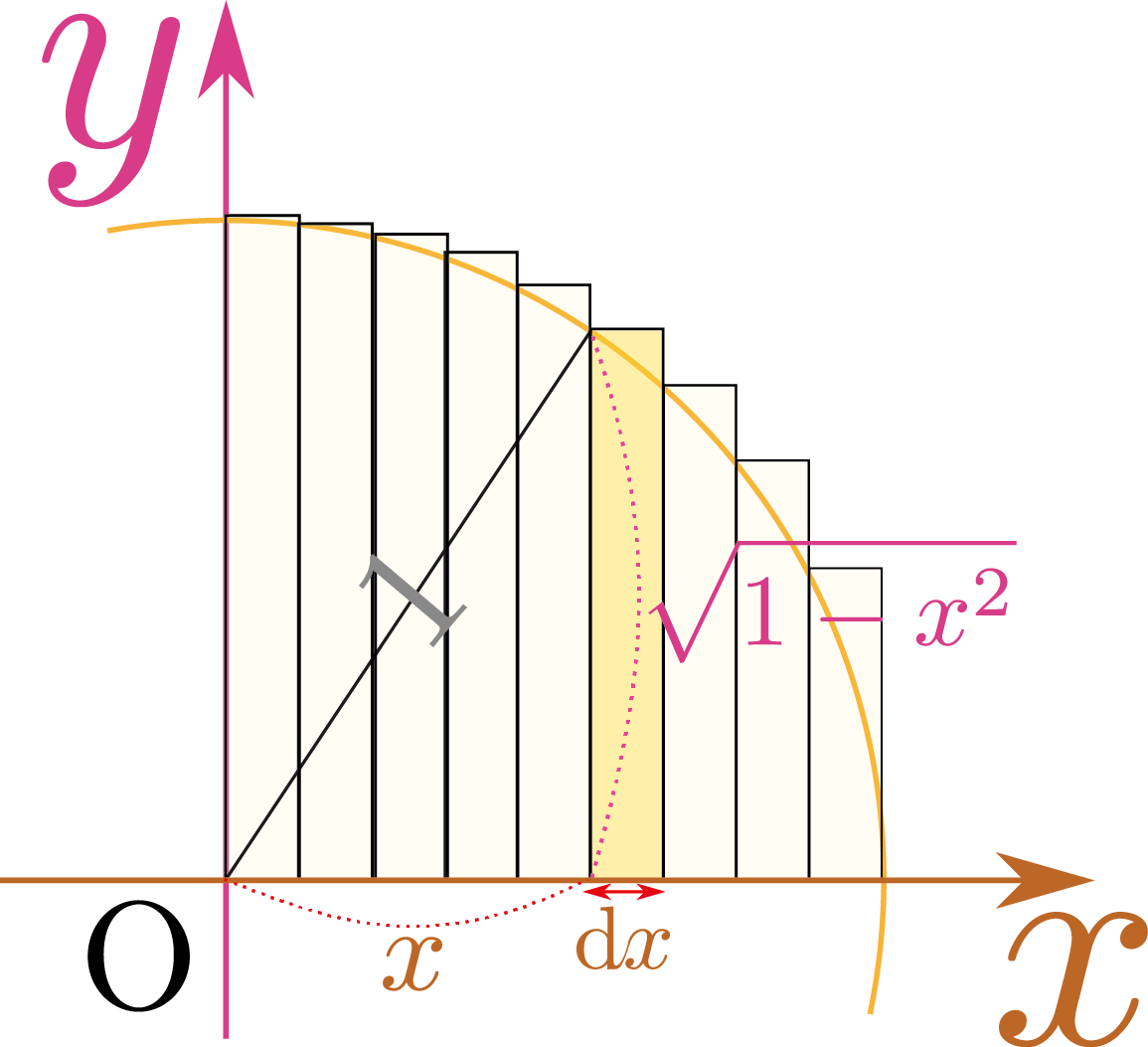
これは高さ${\sqrt{1-\xcol{x}^2}}$で横幅が$\coldx$ である微小な長方形を$\xcol{x}=0$から$\xcol{x}=1$まで変化させながら足していった結果である。グラフを見ればわかるように、それは半径が1の${1\over 4}$円の面積である。そう考えれば答えが${\pi\over 4}$なのは当然と言える。
定積分を使ってこれを計算するために、まず$\xcol{x}=\cos \thetacol{\theta}$と置いてみる。このような「置き換え」は多くの場合、試行錯誤「$\sqrt{1-x^2}$は0から1の範囲で変化する関数だから、$\cos$とかどうかな?」のようにいろいろやってみる。で見つける。ここで考えているように、グラフを描いて図形的に考えてみると、どういう変換を行っているのかが見えてきて、計算の見通しがよくなることもある。
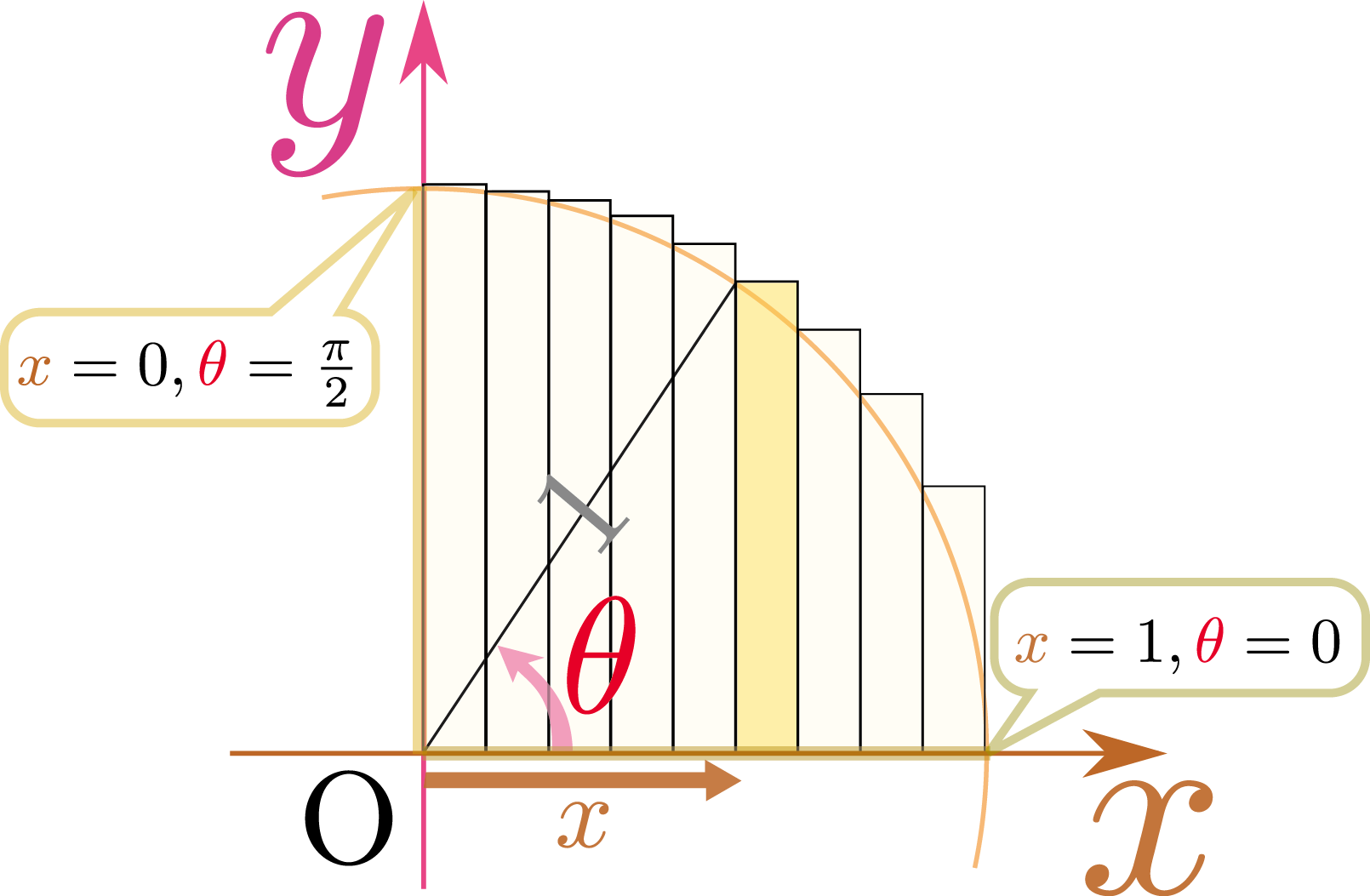
実際、$\thetacol{\theta}$には上に描いたような意味がある。$\xcol{x}=\cos\thetacol{\theta}$なのだから、$\sqrt{1-\xcol{x}^2}=\sin\thetacol{\theta}$であ\linebreak[3]る$\cos ^2\thetacol{\theta}+\sin^2\thetacol{\theta}=1$という式で考えると$\sqrt{1-\xcol{x}^2}=\pm\sin \thetacol{\theta}$となるが、図でわかるように$\thetacol{\theta}$は0から${\pi\over2}$までだから、$\sin\thetacol{\theta}$の前に符号は必要ない。が、それは図に示した長方形の高さである。$\xcol{x}=\cos\thetacol{\theta}$の微分は$\coldx = -\sin\thetacol{\theta} \coldtheta$であるから、$\sqrt{1-\xcol{x}^2}\coldx = -\sin^2\thetacol{\theta} \coldtheta$と置換する。$\xcol{x}=0$のとき$\thetacol{\theta}={\pi\over 2}$、$\xcol{x}=1$のとき$\thetacol{\theta}=0$だから、積分変数を$\xcol{x}\to \thetacol{\theta}$と変える時に積分範囲は$\int_0^1$から$\int_{\pi\over 2}^0$に変わり、さらに反転させて$-\int_0^{\pi\over 2}$となる。
今回の場合、計算すべきは$\int_0^{\pi\over 2}\sin^2\thetacol{\theta} \coldtheta$で、$\sin^2\thetacol{\theta}={1-\cos 2\thetacol{\theta}\over 2}$より、
\begin{equation} \int_0^{\pi\over 2}{1-\cos 2\thetacol{\theta}\over 2}\coldtheta = \left[ {\thetacol{\theta}-{1\over 2}\sin2\thetacol{\theta}\over 2} \right]^{\pi\over 2}_0 ={{\pi\over 2}-{1\over 2}\sin \pi\over 2}-{0-{1\over 2}\sin 0\over 2} ={\pi\over 4} \end{equation} のように積分できる。