積分(続き)
置換積分(続き)
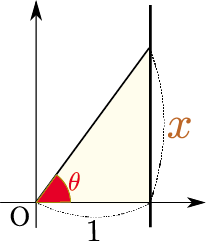
次に、$\int_0^\infty{1\over 1+\xcol{x}^2}\coldx$という積分を考えよう。この積分は、$\xcol{x}=\tan\thetacol{\theta}$($\thetacol{\theta}$の意味は右の図を見よ)と置き換えて、$\coldx={\coldtheta\over \cos^2\thetacol{\theta}}$を使い、 \begin{equation} \int_0^{\pi\over 2}{1\over 1+\tan^2\thetacol{\theta}}\goverbrace{{\coldtheta\over \cos ^2\thetacol{\theta}}}^{\coldx} = \int_0^{\pi\over 2}\coldtheta={\pi\over 2} \end{equation} のように計算できる($1+\tan^2 \theta={1\over \cos^2\theta}$に注意)。図で、$\xcol{x}$を0から$\infty$まで動かしたら$\thetacol{\theta}$がどう変化するかをみれば、積分区間「$\xcol{x}=0$から$\xcol{x}=\infty$」が「$\thetacol{\theta}=0$から$\thetacol{\theta}={\pi\over 2}$」と変わることがわかる。
結果として、${1\over 1+\xcol{x}^2}\coldx=\coldtheta$という置換がされた。この置き換えの意味を図形で理解しておこう。次の図に、底辺1、高さ$\xcol{x}$の直角三角形の高さを$\coldx$だけ大きくしたときの変化を示した。
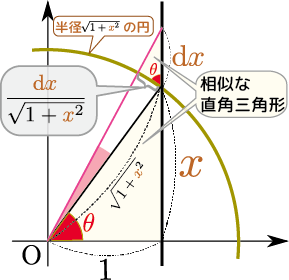
図に描き込まれた円の半径は$\sqrt{1+\xcol{x}^2}$であり、円の一部である中心角$\coldtheta$の扇型を考えると、その扇型の弧の長さは$\sqrt{1+\xcol{x}^2}\times \coldtheta$である(扇型の弧の長さ)$=$(半径)$\times$(中心角)。。
一方、直角三角形の相似を使うと、 \begin{equation} (弧の長さ):\coldx = 1:\sqrt{1+\xcol{x}^2} \end{equation} が成り立つから、(弧の長さ)$={\coldx\over \sqrt{1+\xcol{x}^2}}$である。以上から、$\sqrt{1+\xcol{x}^2}\times \coldtheta={\coldx\over \sqrt{1+\xcol{x}^2}}$が言えて、これからこの積分は角度の積分に書き直すことができて、 \begin{equation} \int_0^\infty {1\over 1+\xcol{x}^2}\coldx=\int_0^{\pi\over 2} \coldtheta={\pi\over 2} \end{equation} と答えが出る。積分の上限が$\infty$でない場合も同様に考えて、 \begin{equation} \int_0^a{1\over 1+\xcol{x}^2}\coldx = \arctan a \end{equation} という式を出せる。たとえば$\int_0^1 {1\over 1+\xcol{x}^2}\coldx={\pi\over 4}$や$\int_0^{1\over\sqrt{3}} {1\over 1+\xcol{x}^2}\coldx={\pi\over 6}$がわかる。ところで、${1\over 1+\xcol{x}^2}$は$|\xcol{x}|<1$なら \begin{equation} {1\over 1+\xcol{x}^2}=1-\xcol{x}^2+\xcol{x}^4-\xcol{x}^6+{\xcol{x}}^8-{\xcol{x}}^{10}+\cdots \end{equation} と展開できるから、 \begin{equation} \int_0^a {1\over 1+\xcol{x}^2}\coldx =\left[\xcol{x}-{\xcol{x}^3\over 3}+{\xcol{x}^5\over 5}-{\xcol{x}^7\over 7}+{{\xcol{x}}^9\over 9}-{\xcol{x}^{11}\over 11}+\cdots\right]_0^a \end{equation} と考えることで、 \begin{equation} \arctan a = a-{a^3\over 3}+{a^5\over 5}-{a^7\over 7}+{{a}^9\over 9}-{a^{11}\over 11}+\cdots \end{equation} とわかる。この$a$に1を代入すると$\arctan 1={\pi\over 4}$になる、というのがライプニッツも発見したという${\pi}$の計算方法である実際計算してみると右辺が${\pi\over 4}$になかなか近づかない。もともとの展開式が$a<1$で使える式だったので収束が遅いのは当然である。$a={1\over \sqrt{3}}$の時に左辺が${\pi\over 6}$になるという計算の方が収束が早い。他にもいろいろな計算方法が知られている。。
上で${\coldx\over 1+\xcol{x}^2}=\coldtheta$と置き換える部分の説明は、図で描くよりも「微分」という計算をした方がわかりやすい人も多いだろう。そう思った人は式の計算で理解しておけばよい。どっちであろうと、自分にわかりやすい方で理解すればよいのはもちろんである。
問題により、そして(思考方法は人それぞれなので)個人により、「どう考えれば理解しやすいか」は違う。では「式で計算できればそれでよい」(または「図解できればそれでよい」)かというと、次に現れる問題があなたにとってどちらで理解しやすいかはわからないわけだから、いろんな方法で理解することを(少なくとも``数学修行''をしている間は)心がけておいた方がいいだろう。
ときどきたくさん教えられてもわかんなくなるから、教える方法は一つにしてくださいという人がいるのだが、一つしか武器がない状態では太刀打ちできない強敵に出会う時のために、修行はしておこう。
立ち向かう相手(自然現象)は強大なのだから持っている武器は多い方がよい。
三角関数を使った置換積分
定積分を実行した時にやった置換積分を使うことで、複雑に見える関数の積分を実行することができる。たとえば、$\xcol{x}=\cos\thetacol{\theta}$とおくとその微分に関しては$\coldx =-\underbrace{\sin\thetacol{\theta}}_{\pm\sqrt{1-\xcol{x}^2}} \coldtheta $複号$\pm$のどちらを取るかは、今$\sin \thetacol{\theta}$や$\cos \thetacol{\theta}$がどのような値を取っている領域で考えているのかを見て決めるべきである。$\coldx$と$\coldtheta$の正負の関係は、角度によって違う。という置換ができる。これを整理すると${\coldx \over \sqrt{1-\xcol{x}^2}}= \pm\coldtheta$となるので、$\sqrt{1-\xcol{x}^2}$を含むような複雑な式が出てきた時は、これを使って積分を$\thetacol{\theta}$の積分に変えることができる。たとえば\節{tikandeha}では \begin{equation} \int_0^1 \sqrt{1-\xcol{x}^2}\coldx = \int_0^1 (1-\xcol{x}^2){\coldx\over \sqrt{1-\xcol{x}^2}}=\int_0^{\pi\over 2} \sin^2\thetacol{\theta} \coldtheta \end{equation} という変形を行ったこの時は${1\over \sqrt{1-\xcol{x}^2}}\coldx=-\coldtheta$のように符号を選んだ(考えている領域では$\xcol{x}$が増えると$\thetacol{\theta}$が減ったから)うえで積分の範囲をひっくり返した時にもう一度符号が出た。。同様に、 \begin{equation} \intdx {1\over \sqrt{1-\xcol{x}^2}} = \int \coldtheta =\thetacol{\theta}+C=\arccos \xcol{x} +C\label{int} \end{equation} のような積分が可能である。$\xcol{x}=\cos\thetacol{\theta}$と置いて計算を始めたから、最後で$\thetacol{\theta}=\arccos \xcol{x}$と戻した。実はこうできるかどうかは$\thetacol{\theta}$の範囲による。
ここで、$\xcol{x}=\sin \thetacol{\theta}$とおいても同様のことができるので、 \begin{equation} \intdx {1\over \sqrt{1-\xcol{x}^2}} =\arcsin \xcol{x} +C \end{equation} という式を作ることができて、これも正しい。「$\sin $でも$\cos $でも正しいなんて変ではないか」と思うかもしれないが、$\sin \left(\thetacol{\theta}+{\pi\over 2}\right)=\cos \thetacol{\theta}$のような式があるから、角度を平行移動すれば$\sin$は$\cos$になる(逆も同様)。つまり積分定数の違いでどちらになってもよい(同様に、$\sin\kakko{\thetacol{\theta}+\pi}=-\sin\thetacol{\theta}$のような式もあるので、 \begin{equation} \intdx {1\over \sqrt{1-\xcol{x}^2}} =-\arcsin \xcol{x} +C \end{equation} という式も、正しい(もちろん、正しく積分定数を調整するという前提のもとでである)。
${1\over 1+\xcol{x}^2}$が出てくる積分は$\xcol{x}=\tan\thetacol{\theta}$と置くことで簡単化できる。というのは、$\coldx = {1\over \cos^2\thetacol{\theta} }\coldtheta = (1+\tan^2\thetacol{\theta})\coldtheta$という変形から、${1\over 1+\xcol{x}^2}\coldx = \coldtheta$と変形していくことができるからである。これから、 \begin{eqnarray} \intdx {1\over 1+\xcol{x}^2} &=& \int \coldtheta = \thetacol{\theta}+C=\arctan \xcol{x} +C\\ \intdx {\xcol{x}\over 1+\xcol{x}^2} &=&\int\coldtheta \tan \thetacol{\theta} = -\log\kakko{\cos\thetacol{\theta}}+C = {1\over 2}\log\underbrace{ \left( {1\over\cos^2\thetacol{\theta}} \right)}_{1+\tan^2\thetacol{\theta}}+C\nonumber\\[-4mm] &=&{1\over 2}\log\kakko{1+\xcol{x}^2}+C \end{eqnarray} のように下の式は$1+\xcol{x}^2=\tcol{t}$という置換積分でも計算可能。積分をしていくことができるこういうのはいちいち公式を覚えようとしなくてよい(「覚えよう」は禁句)から、「${1\over\sqrt{1-\xcol{x}^2}}\coldx$がでてきたら$\xcol{x}=\sin \thetacol{\theta}$ではどうか?」とか「${1\over 1+\xcol{x}^2}$が出てきたら$\xcol{x}=\tan\thetacol{\theta}$と置いてはどうか?」などと考えていくのがよい。。
双曲線関数を使った置換積分
では、たとえば${1\over\sqrt{1+\xcol{x}^2}}\coldx$が出てきたらどうしよう??---この形の積分が簡単になるような関数はあるだろうか?---そもそも、「${1\over\sqrt{1-\xcol{x}^2}}\coldx$がでてきたら$\xcol{x}=\sin \thetacol{\theta}$」という考えがうまくいったのは、$\xcol{x}=\sin\thetacol{\theta}$の微分が$\coldx=\cos\thetacol{\theta}\coldtheta$で、${\coldx\over \sqrt{1-\xcol{x}^2}}=\coldtheta$となったからであった。そこで、$\xcol{x}=f\kakko{\thetacol{\theta}}$と置いたとき、$f'(\thetacol{\theta})=\sqrt{1+\xcol{x}^2}$になるような関数があればこの積分ができる。そういう関数として知られているのが、「双曲線関数」と呼ばれる関数群の一つである$\sinh \thetacol{\theta}$である三角関数に似ているところがあるので$\thetacol{\theta}$という文字で変数を表しておくが、この$\thetacol{\theta}$には「角度」という意味は全くない。。$\sin,\cos$のテイラー展開では次数が上がるごとに符号が反転するが、以下のように符号が反転しない \begin{eqnarray} \sinh \thetacol{\theta} &=& \thetacol{\theta}+{\thetacol{\theta}^3\over 3!}+{\thetacol{\theta}^5\over 5!}+\cdots=\sum_{n=0}^\infty {\thetacol{\theta}^{2n+1}\over (2n+1)!}\label{defsinh}\\ \cosh \thetacol{\theta} &=& 1+{\thetacol{\theta}^2\over 2!}+{\thetacol{\theta}^4\over 4!}+\cdots=\sum_{n=0}^\infty {\thetacol{\theta}^{2n}\over (2n)!}\label{defcosh} \end{eqnarray} のような展開級数を作る。これらの関数が双曲線関数($\sinh$と$\cosh$)三角関数の${\sin \thetacol{\theta}\over \cos \thetacol{\theta}}=\tan\thetacol{\theta}$と同様に、${\sinh\thetacol{\theta}\over \cosh\thetacol{\theta}}=\tanh \thetacol{\theta}$という関数もある。である正確な読み方は$\sinh$は「ハイパボリックサイン」(または「サインハイパボリック」)、$\cosh$は「ハイパボリックコサイン」(または「コサインハイパボリック」)である$\sinh$を「しんち」、$\cosh$を「こっしゅ」などと読むこともある。。すぐにわかるように、 \begin{eqnarray} \ddtheta\cosh \thetacol{\theta}=\sinh \thetacol{\theta},~~ \ddtheta\sinh\thetacol{\theta}=\cosh\thetacol{\theta}\label{hbibun} \end{eqnarray} である(ここでも、三角関数にはあるマイナス符号がない)。 \begin{eqnarray} \cosh \thetacol{\theta} +\sinh \thetacol{\theta}&=& 1+ \thetacol{\theta}+{\thetacol{\theta}^2\over 2!}+{\thetacol{\theta}^3\over 3!}+{\thetacol{\theta}^4\over 4!}+\cdots =\sum_{n=0}{\thetacol{\theta}^n\over n!}=\E^\thetacol{\theta} \\ \cosh \thetacol{\theta} -\sinh \thetacol{\theta}&=& 1- \thetacol{\theta}+{\thetacol{\theta}^2\over 2!}-{\thetacol{\theta}^3\over 3!}+{\thetacol{\theta}^4\over 4!}-\cdots =\sum_{n=0}{(-\thetacol{\theta})^n\over n!}=\E^{-\thetacol{\theta}} \end{eqnarray} のように足したり引いたりすることで指数関数になる。
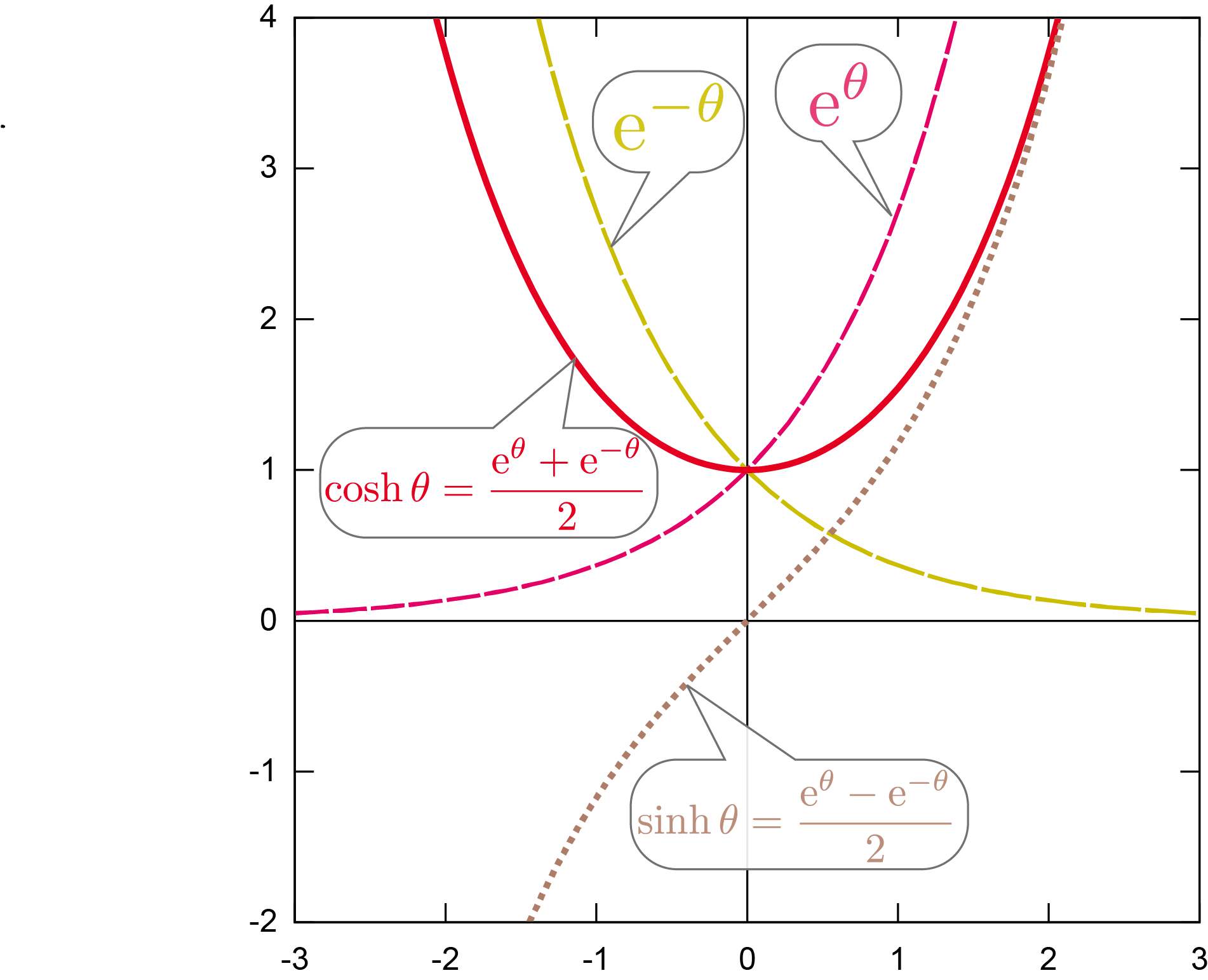
この式はオイラーの関係式$\E^{\mathrm i\thetacol{\theta}}=\cos\thetacol{\theta}+\I\sin \thetacol{\theta}$の$\I$がなくなった式であるとも言える。
$\cosh$と$\sinh$のグラフは右のようになる。$\E^\theta\times \E^{-\theta}=1$から \begin{equation} \begin{array}{rl} & \goverbrace{(\cosh\thetacol{\theta}+\sinh\thetacol{\theta})}^{\E^{\thetacol{\theta}}} \goverbrace{(\cosh\thetacol{\theta}-\sinh\thetacol{\theta})}^{\E^{-\thetacol{\theta}}}\\[3mm] &= \cosh^2\thetacol{\theta}-\sinh^2\thetacol{\theta} =1\label{coshsinh} \end{array} \end{equation} がわかる($\cos^2\thetacol{\theta}+\sin^2\thetacol{\theta}=1$に似た式である)。
また、逆に解くことで以下を得る。 \begin{equation} \cosh\thetacol{\theta}={\E^\thetacol{\theta}+\E^{-\thetacol{\theta}}\over 2},\sinh\thetacol{\theta}={\E^{\thetacol{\theta}}-\E^{-\thetacol{\theta}}\over 2} \end{equation}
$\xcol{x}=\cosh\thetacol{\theta},\ycol{y}=\sinh\thetacol{\theta}$としてグラフを描くと下のようになる。
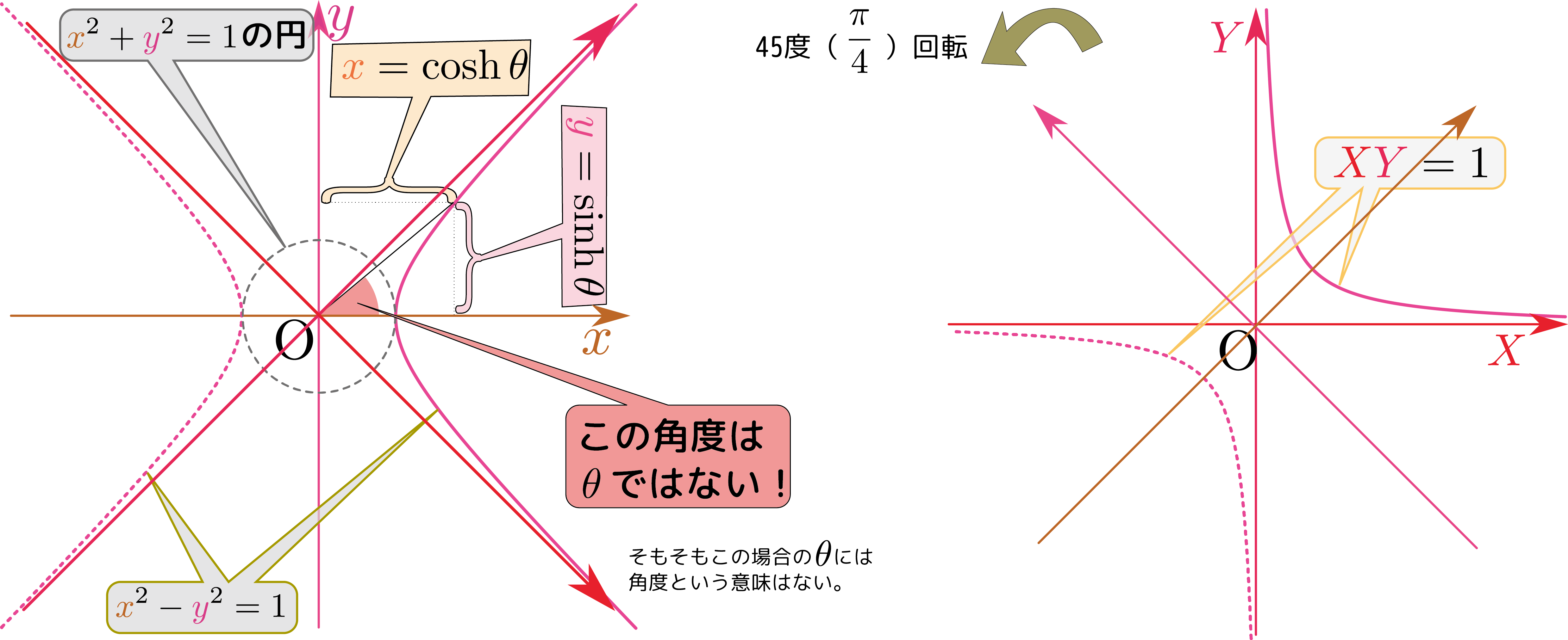
これが「双曲線関数」という名前の由来である。「双曲線」と言われると思い出すのは$\ycol{y}={1\over \xcol{x}}$(いわゆる「反比例」の式とグラフ)の方かもしれない。$\tcol{Y}={1\over \zcol{X}}$すなわち$\zcol{X}\tcol{Y}=1$と$\xcol{x}^2-\ycol{y}^2=1$は、\ang{45}(${\pi\over 4}$ラジアン)回転させた関係にある。それ$\zcol{X}=\xcol{x}+\ycol{y},\tcol{Y}=\xcol{x}-\ycol{y}$を代入することでこの二つの式が入れ替わる$\zcol{X}\tcol{Y}=\xcol{x}^2-\ycol{y}^2$ということからもわかる。
さて、$\xcol{x}=\sinh \thetacol{\theta}$と置換した場合どうなるかを考えよう。微分して$\coldx=\cosh \thetacol{\theta} \coldtheta$であるが、$\cosh \thetacol{\theta}=\sqrt{1+\sinh^2\thetacol{\theta}}$である($\cosh \thetacol{\theta}$は定義からして正にしかならないので、$\sqrt{~}$の前に$\pm$はいらない)。よって、${\coldx\over \sqrt{1+\xcol{x}^2}}=\coldtheta$という置き換えができて、${1\over \sqrt{1+\xcol{x}^2}}$の積分が可能になる。たとえば、 \begin{equation} \intdx{1\over\sqrt{1+\xcol{x}^2}}={\rm arcsinh}~ \xcol{x} +C \end{equation} である(${\rm arcsinh}$は$\sinh$の逆関数)。
面積・体積と積分
円錐の体積
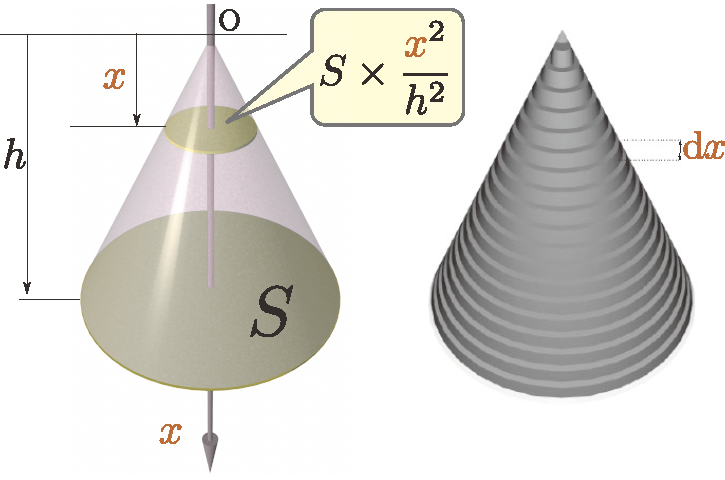
円錐や角錐の体積は底面積を$S$、高さを$h$とすると、${1\over 3}Sh$で書ける。これを定積分を使って出そう。頂点を原点として、底面に垂直な方向の距離を考えて、その距離$\xcol{x}$とする(面に垂直な下向きの方向に$\xcol{x}$軸を取る)。$\xcol{x}$は下向きに取っているので、『高さ』とは逆になっていることに注意しよう。
そして定積分の精神に従って、この$\xcol{x}$を微小区間に切り刻み、その一つの微小区間の幅(この円錐や角錐をビルと考えた時の「一階の高さ」である)を$\coldx$とする(座標$\xcol{x}$から座標$\xcol{x}+\coldx$までを切り取って考える)。

この一階の体積は、この階の底面積$\times \coldx$である。面積はスケールの自乗に比例するから、底面積は$S\times{\xcol{x}^2\over h^2}$である(図では円錐の場合を示したが、角錐であっても同様)から、 \begin{equation} \int_0^h {S\xcol{x}^2\over h^2}\coldx =\left[ {S\xcol{x}^3\over 3h^2} \right]_0^h={Sh\over 3} \end{equation} となる。分母の3は$\int_a^b\xcol{x}^2\coldx=\left[{\xcol{x}^3\over 3}\right]_a^b$から来たのである。
ここで体積を計算した方法からすると、円錐や角錐の頂点が(底面に平行な方向に)移動したとしても体積が変わらない(つまり体積は底面積と高さだけで決まり、傾きにはよらない)ことが納得できる。これは円柱などの場合でも同じである。
球の体積
球も同様に微小な高さ$\coldx$に分けて考える。
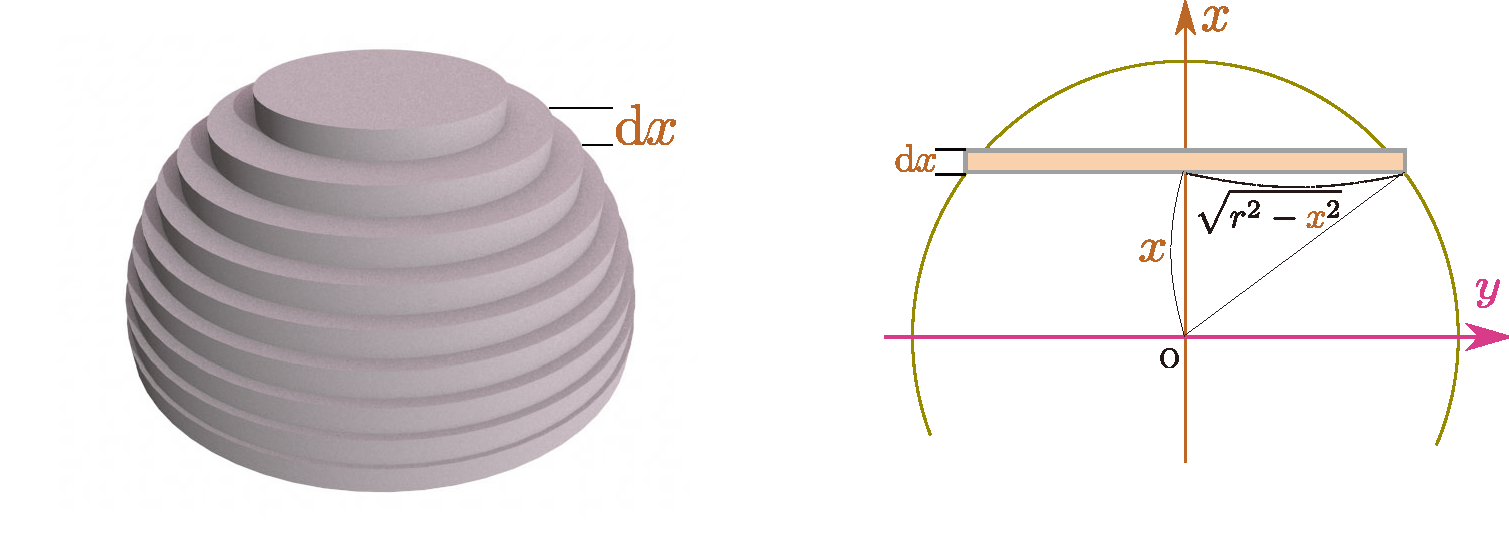
今度は$\xcol{x}=0$は球の中心におくと、図に描いたように、各階の床は半径$\sqrt{r^2-\xcol{x}^2}$の円で、底面積$\pi(r^2-\xcol{x}^2)$を持つ。これに高さ$\coldx$を掛ければ一階分の体積が出るから、範囲$-r < x < r$でこれを積分して、 \begin{equation} \int_{-r}^r \pi(r^2-\xcol{x}^2)\coldx =\pi\left[ r^2 \xcol{x}-{\xcol{x}^3\over 3} \right]_{-r}^r =\pi\left( r^3-{r^3\over 3}-\left( -r^3 + {r^3\over 3} \right)\right)={4\pi r^3\over 3} \end{equation} となる。
同じ結果ではあるが、球を水平に切るのではなく、小さい球殻から大きい球殻へと(風船を膨らますように)足算する方法もある。球の表面積が$4\pi r^2$であることを使って \begin{equation} \int_{0}^r 4\pi\xcol{x}^2\coldx =4\pi\left[{\xcol{x}^3\over 3}\right]_{0}^r={4\pi r^3\over 3} \end{equation} のように計算する方法もある。
曲線の長さ
$\ycol{y}=f\kakko{\xcol{x}}$で表現されるグラフの線の長さを計算してみよう。微小な区間$(\xcol{x},\ycol{y})$から$(\xcol{x}+\coldx,\ycol{y}+\coldy)$の長さは$\sqrt{\coldx^2+\coldy^2}$であるから、これを足していく。ここで、 \begin{equation} \sqrt{\coldx^2+\coldy^2} =\sqrt{1+\left({\coldy\over \coldx}\right)^2}\coldx \end{equation} という変形をする。この微小区間の長さを足算していけばよい。$\xcol{x}$を独立変数、$\ycol{y}$を従属変数と考えることにすれば、これは普通の積分になっている。$(a,f\kakko{a})$から$(b,f\kakko{b})$に達する線の長さは \begin{equation} \int_a^b \sqrt{1+\left({\coldy\over \coldx}\right)^2}\coldx \end{equation} という積分で得られる。
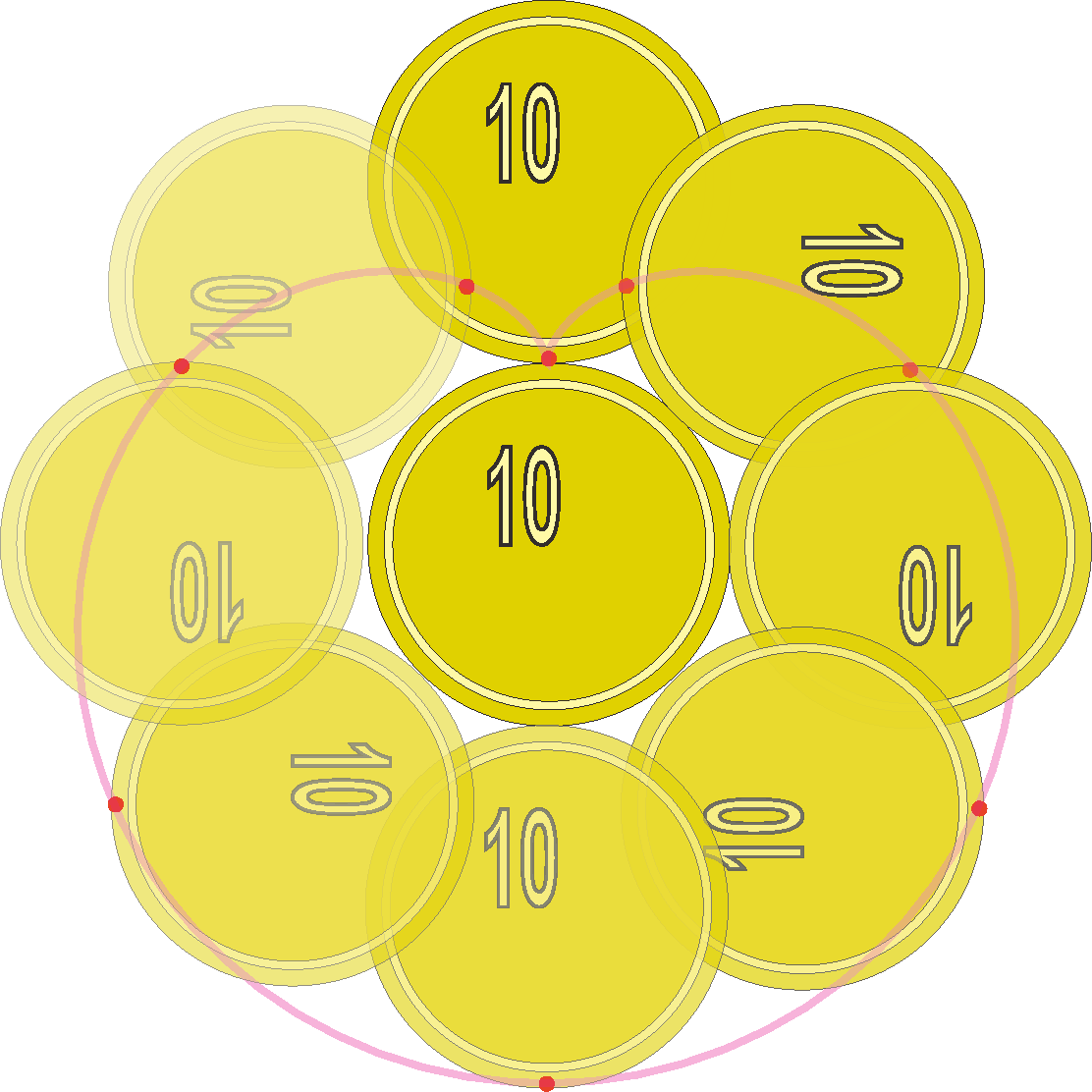
少し難しい例で曲線の長さを出してみよう。硬貨を2枚机の上において、一方を固定してもう一方をその周りにぐるりと廻してみる(この時、硬貨と硬貨の接触点はすべらないようにする)。
動かした方の硬貨が一周して元に戻ってきたとき、この硬貨の縁の一点(たとえば、図に赤で示した点、以下「移動点」と呼ぶ)はどれだけの距離を動いているだろうか??---図に示したように、この軌跡はハートマークのような形を描く(「カージオイド」と呼ばれている)。
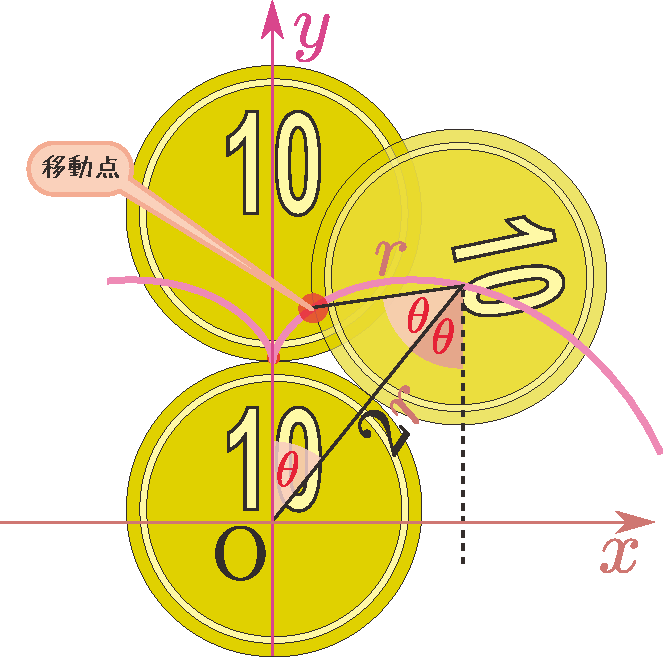
まずこの移動点の位置は(上図のように考えると)動かしている方の硬貨が元の位置から$\thetacol{\theta}$だけ回ると、硬貨自体の回転はその2倍の角度だけ回転していることに注意。このことは、一周してくる間に2回、10円玉の向きが\ovalbox{10}になっていることからもわかる。、 \begin{eqnarray} \xcol{x}&=& 2r \sin\thetacol{\theta} -r \sin 2\thetacol{\theta}\\ \ycol{y}&=& 2r \cos\thetacol{\theta} -r \cos 2\thetacol{\theta} \end{eqnarray} である$\thetacol{\theta}$が通常と違って、$\ycol{y}$軸のところで$\thetacol{\theta}=0$であることにも注意。縦に硬貨が並んだ状態を初期状態($\thetacol{\theta}=0$)にしたかったので。から、$\thetacol{\theta}$が微小変化したとして$\xcol{x},\ycol{y}$の微小変化は \begin{eqnarray} \coldx &=& 2r(\cos \thetacol{\theta} - \cos 2\thetacol{\theta})\coldtheta\\ \coldy &=& -2r(\sin \thetacol{\theta} - \sin 2\thetacol{\theta})\coldtheta \end{eqnarray} であり、この微小部分の長さは$\sqrt{\left({\coldx\over \coldtheta}\right)^2 + \left({\coldy\over \coldtheta}\right)^2}\coldtheta$で与えられるのでまずルートの中身を計算すると、 \begin{equation} \begin{array}{rll} \left({\coldx\over \coldtheta}\right)^2 + \left({\coldy\over \coldtheta}\right)^2 =& 4r^2\left( (\cos \thetacol{\theta} - \cos 2\thetacol{\theta})^2 +(\sin \thetacol{\theta} - \sin 2\thetacol{\theta})^2 \right)\\ =& 4r^2\left( 2-2\cos \thetacol{\theta}\cos 2\thetacol{\theta}-2\sin \thetacol{\theta}\sin 2\thetacol{\theta} \right)&\kokode{加法定理{\cos \thetacol{\theta}\cos 2\thetacol{\theta}+\sin \thetacol{\theta} \sin 2\thetacol{\theta}\atop =\cos \kakko{2\thetacol{\theta}-\thetacol{\theta}}}}\\ =& 8r^2\left(1-\cos \thetacol{\theta}\right)&\kokode{半角公式{1-\cos \thetacol{\theta}\over 2}=\sin ^2{\thetacol{\theta}\over 2}}\\ =& 16r^2\sin ^2{\thetacol{\theta}\over 2} \end{array} \end{equation} となり、微小部分の長さが$4r\left|\sin{\thetacol{\theta}\over 2}\right|\coldtheta$(絶対値に注意!)であることがわかる。$\sin{\thetacol{\theta}\over 2}$は$0<\thetacol{\theta}<\pi$では正で、$\pi<\thetacol{\theta}<2\pi$では負であることに注意して、これを定積分して、 \begin{equation} \int_0^{2\pi}4r\left| \sin{\thetacol{\theta}\over 2}\right|\coldtheta =8r\int_0^\pi \sin{\thetacol{\theta}\over 2}\coldtheta= 8r\left[-2\cos {\thetacol{\theta}\over 2}\right]^{\pi}_0=16r \end{equation} が全体の長さである(円が関係するのに答えには$\pi$が含まれないという、面白い結果が出る)。