常微分方程式(続き)
変数分離できる一階微分方程式
まず微分方程式がどういうものかに慣れることが必要だと思うので、以下では、微分方程式の中でも比較的簡単(でも応用範囲は広い)な「変数分離できる一階微分方程式」の具体例を考えていこう。
前に例として上げた${\coldy\over \coldx}=\ycol{y}$は変数分離できる微分方程式の例であり、「変数分離した後で積分」という方法で解くことができた。
\begin{equation} \begin{array}{rll} {\coldy\over \coldx}=&\ycol{y}&\kokode{変数分離}\\ {\coldy\over \ycol{y}}=&\coldx&\kokode{積分}\\ \log \ycol{y} =&\xcol{x}+C \end{array} \end{equation}
変数分離はいつでもできるとは限らない。たとえば${\coldy\over \coldx}=\xcol{x}+\ycol{y}$という簡単な場合でも左辺に$\ycol{y}$だけを集めることはできない(この微分方程式は解ける。つまり変数分離できなくても解ける時は解ける)。以下この節では「変数分離できる場合」に限って話をする。
もう一つ、簡単な例を示そう。${\coldy\over \coldx}=-{\xcol{x}\over \ycol{y}}$という式(前に図で考えた微分方程式で、答は円であった)は書き直すと$\ycol{y}\coldy = -\xcol{x} \coldx $と変数分離でき、$\int \ycol{y}\coldy = -\int\xcol{x} \coldx$と積分すれば \begin{equation} \begin{array}{rl} {\ycol{y}^2\over 2}=&-{\xcol{x}^2\over 2}+C \end{array} \end{equation} が出る($C$は積分定数)。結果を整理すると、$\xcol{x}^2 +\ycol{y}^2 = 2C$という半径$\sqrt{2C}$の円の式が出てくる。
ここで、解を$\ycol{y}=f\kakko{\xcol{x}}$の形にまでもって行かなくてもよい。実際、今の場合では$\ycol{y}=f\kakko{\xcol{x}}$の形にしようとすると、$\ycol{y}=\pm\sqrt{2C-\xcol{x}^2}$のように複号が必要になって、かえって厄介になる。
次に${\coldy\over \coldx}={\ycol{y}\over \xcol{x}}$を同様に解いてみよう(図で考えたとき、この解は「原点を通る直線」であった)。まず変数分離して${\coldy\over \ycol{y}}={\coldx\over \xcol{x}}$としてから積分すると、 \begin{equation} \begin{array}{rll} \log \ycol{y} =& \log \xcol{x} +C&\kokode{両辺を\E の肩へ}\\[-2mm] \ycol{y}=& \xcol{x}\E^C \end{array} \end{equation} となり、確かに(傾き$\E^C$の)直線が解である(図を描いて考える方がすっとわかる)。
実例:ロケットの速度変化
燃料を噴射して飛ぶロケットの噴射した燃料の量と速度変化の関係は微分方程式から求めることができる。もし、我々が微分方程式というものを知らずにいいかげんな考え方をすると、
大間違い
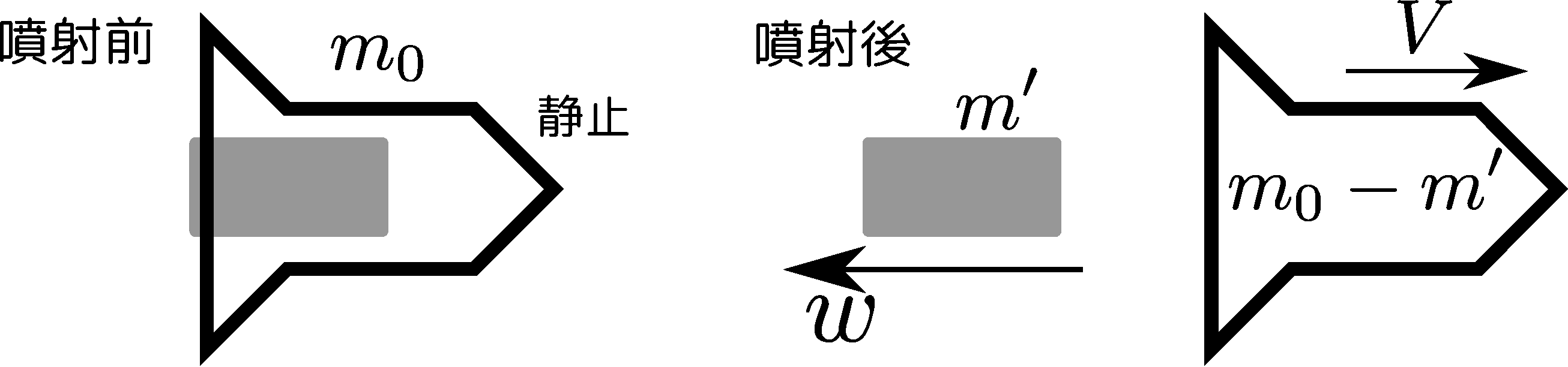
静止していた質量$m_0$のロケットが質量$m'$の推進剤(燃料を燃焼させた結果であるガスなど)を速さ$w$で後方に噴射した。噴射後のロケットが速さ$V$になる。
をしてしまう。この間違った考え方からすると、運動量の保存により外部から力が加わらない時は運動量すなわち質量$\times$速度が保存されるという物理法則がある。ここではこの法則を使ってロケットの速度を計算している。、 \begin{equation} 0=(m_0-m')V +m'\times (-w) \end{equation} が成り立つ。結果として、$V={m'\over m_0-m'}w$となるが、これは大間違いなのだ念のため、運動量保存則自体は間違いではない。。
上の大間違いは、「ロケットの質量も速度も連続的に少しずつ変化していく量なのにまるで一気に変わったかのように考えてしまった」点が間違いである自然は飛躍しないという言葉があるが、それは「自然現象は微小変化の積み重ねで起こる」ということだと解釈できる。連続的に少しずつ変化していく量は微積分を使って表現しなくてはいけない。ここから下では、$\aka{m}$や$\ao{V}$は連続的に変化する変数(色付き)として扱う。。すぐ後で述べるように推進剤の速さは外部から見て一定にならないという点も間違っている。そこで、(全体の変化を一気に考えるのではなくそのうちの一部を取り出して)微小変化について絵を描くと以下のようになる。
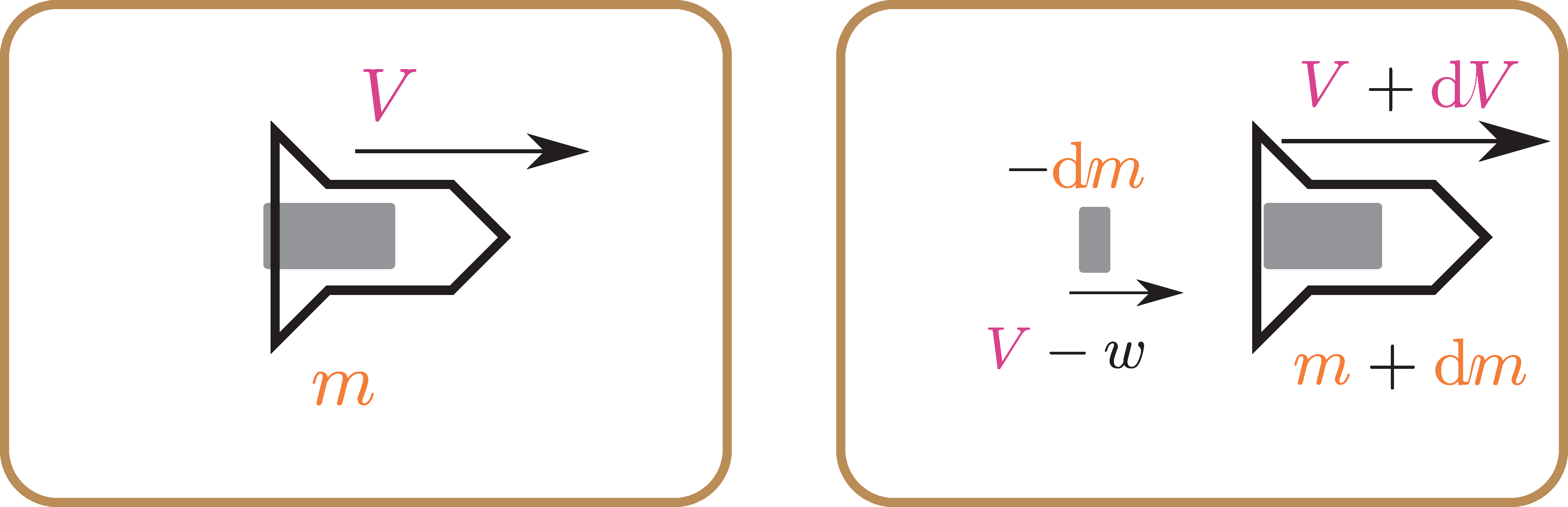
上の図はすでにある程度噴射した途中の状態で、すでに速度$\ao{V}$を持っている。この時の質量は最初の$m_0$に比べて少ない$\aka{m}$(←変数!)になっている。微小時間後に、ロケットは質量$\aka{m}+\akadm$で速度$\ao{V}+\aodV$になっている。
ここで、噴射された質量が$-\akadm$であることに注意。$\akadm$は「質量の変化量」であるから、質量が減っていく状況においては負の量であることに注意しよう---「減ってるんだから引かなきゃ」と(気を利かせたつもりで)噴射後の質量を「$\aka{m}-\akadm$」としてしまうのはよくある間違いで、やってはいけない。$\akadm$など$\diff $のついた量はあくまで「変化量」であり、減る時は$\akadm<0$であると考えていかないと、積分結果がおかしなことなってしまう。というより、変化量を$+\akadm$とすることで、増えるなら$\akadm>0$(減るなら$\akadm<0$)と計算ができるようになっている。
もう一つ、噴射された推進剤は「大間違い」の図のように$w$の速度で後方へ進むとは限らず、速度$w-\ao{V}$で後方へ進む(または「速度$\ao{V}-w$で前方へ進む」)ことにも注意が必要である。既に速度$\ao{V}$を持っているロケット見て「$w$の速さ」で後方に噴射されたのだから、$w$ではなく速度$w-\ao{V}$になる、と考えればよい。あるいは、噴射前に$\ao{V}$の速度で右に飛んでいたものが、噴射により左向き$w$の速度を与えられたから、右向き$\ao{V}-w$の速度になった、とも考えられる。
$w-\ao{V}<0$の時、噴射剤は前方(!?)に進む。$w=\ao{V}$のとき、噴射された推進剤はその場に静止する(ロケットから見たら後方に動いている)。以上に注意しつつ運動量保存則を考えると、 \begin{equation} \aka{m} \ao{V} = (\aka{m}+\akadm)(\ao{V}+\aodV) -\akadm (\ao{V}-w) \end{equation} となる。この式を整理すると、 \begin{equation} \begin{array}{rl} \gunderbrace{\aka{m}\ao{V}}_{相殺→}=&\gunderbrace{\aka{m}\ao{V}}_{←相殺} + \gunderbrace{\akadm \ao{V}}_{\text{{相殺}{→}}}+ \aka{m}\aodV +\gunderbrace{\akadm \aodV}_{高次の微小量} \gunderbrace{-\akadm \ao{V}}_{{{相殺}{←}}}+ \akadm w \\ -\aka{m}\aodV=& \akadm w \\ \end{array} \end{equation} となる。変数分離して$\aodV= -w {\akadm \over\aka{m}}$としてから積分すると結果は \begin{equation} \ao{V}=-w\log \aka{m} +C \end{equation} である。初期条件$\aka{m}=m_0$(初期値)の時に$\ao{V}=V_0$より$C=w\log m_0+V_0$となるので、 \begin{equation} \ao{V}=-w\log \aka{m} +\goverbrace{w\log m_0+V_0}^C = w\log\kakko{{m_0\over \aka{m}}}+V_0 \end{equation} となり、速度変化$\ao{\Delta V}$に関して以下が成立する。
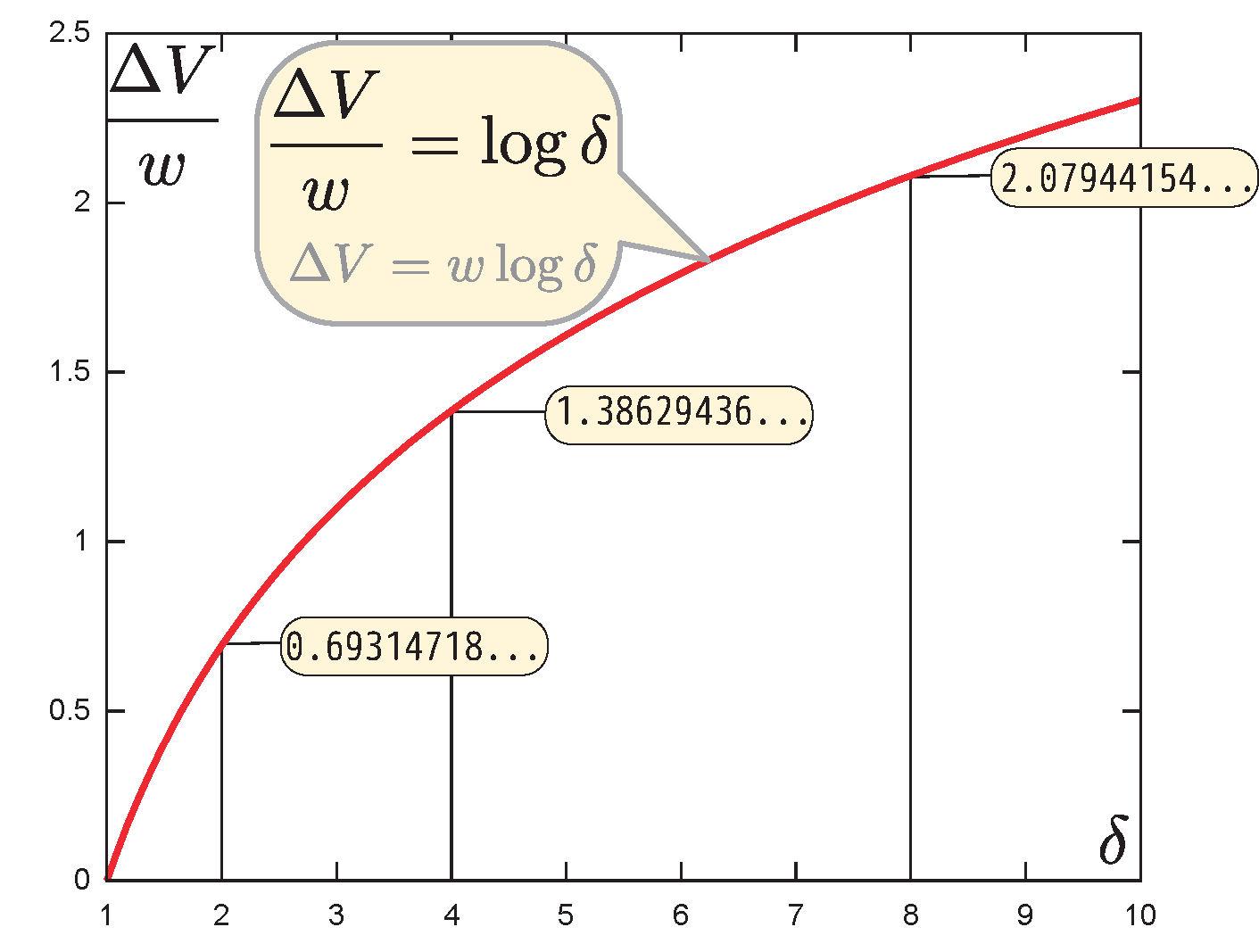
\begin{equation} \gunderbrace{\ao{V}-V_0}_{\ao{\Delta V}}= w\log\kakko{{m_0\over \aka{m}}}\label{wlogv} \end{equation}
最終的にロケット全体の質量が$m_1$になったところで推進剤が尽きたとすると、そのときの速度変化は$\ao{\Delta V}=w\log\kakko{{m_0\over m_1}}$となる。
$\delta={m_0\over m_1}$この$\delta$は変化量を表す$\delta$ではなく、「$\delta$」1文字で一つの数。は「質量比」(文字通り、噴射前と噴射後の質量の比)と呼ばれる。グラフで分かるように、$\delta$を大きくしても$\ao{{\Delta V}}$はどんどん増えるというわけにはいかない($\log x$という関数は傾き${1\over x}$だから、傾きがどんどん緩くなる)。性能を上げるには噴射速度$w$(燃料の質に大きく左右される)が大事であることがわかる。
実例:兵力自乗の法則
二つの軍隊が戦争をしている。それぞれの兵力を$\aka{A},\ao{B}$とする。時間が経つと、$\aka{A}$は$\ao{B}$に比例して減り、$\ao{B}$は$\aka{A}$に比例して減るから、 \begin{eqnarray} \aka{\diff A} &=& -\alpha \ao{B} \coldt,~~ \ao{\diff B}=-\alpha \aka{A} \coldt \end{eqnarray} という式が成立する。このいわば「連立微分方程式」を$(第1式)\times \aka{A}-(第2式)\times \ao{B}$と計算すると、 \begin{equation} \begin{array}{rl} \aka{A}\aka{\diff A} - \ao{B}\ao{\diff B}=&-\alpha \aka{A}\ao{B}\coldt +\alpha \aka{A}\ao{B}\coldt \\ \diff (\aka{A}^2-\ao{B}^2)=&0\\ \end{array} \end{equation} となり、$\aka{A}^2 -\ao{B}^2 = 一定$という式が導かれる。これは「兵力自乗の法則」(またはランチェスターの第2法則)として知られる。たとえば最初$\ao{B}=B_0,\aka{A}=2B_0$だった($\aka{A}$の方が2倍の兵力を持っていた)場合、$\aka{A}^2 -\ao{B}^2 =3(B_0)^2$となるから、$\aka{A}=\sqrt{3}B_0$になったところで$\ao{B}=0$となる。$\ao{B}$の兵力が文字通り全滅軍事用語で「全滅」は「全兵力が死んだ」という意味ではなく、兵力として機能しなくなった状態を意味していて、$\ao{B}\simeq 0.7B_0$ぐらいでもう「全滅」と判定する。ここで「文字通り全滅」と書いたのは$\ao{B}=0$という意味。した時、$\aka{A}$は($2{B_0}\to\sqrt{3}B_0$と変化したので)最初の${\sqrt{3}\over 2}\fallingdotseq0.87$倍が残っている。もし敵の3倍の兵力を用意できれば、$\aka{A}^2 -\ao{B}^2 =8(B_0)^2$なので$\aka{A}=\sqrt{8}B_0$になったところで$\ao{B}=0$となり、元の兵力の${\sqrt{8}\over 3}\fallingdotseq0.94$倍が残るいろんな数字を入れて計算してみよう。「戦力の集中」が戦争においては大事だということが実感できる。。
以上を示すアニメーションが、 にある。
実例:流行の方程式
ある流行(服でも靴でも帽子でもいい)がどのように時間的に流行していくか」を、微分方程式で考えてみる。以下では帽子の場合で説明しよう。
説明のアニメーションが、 にある。
この結果をグラフにすると次のようになる(グラフは$k$を変化させた場合)。
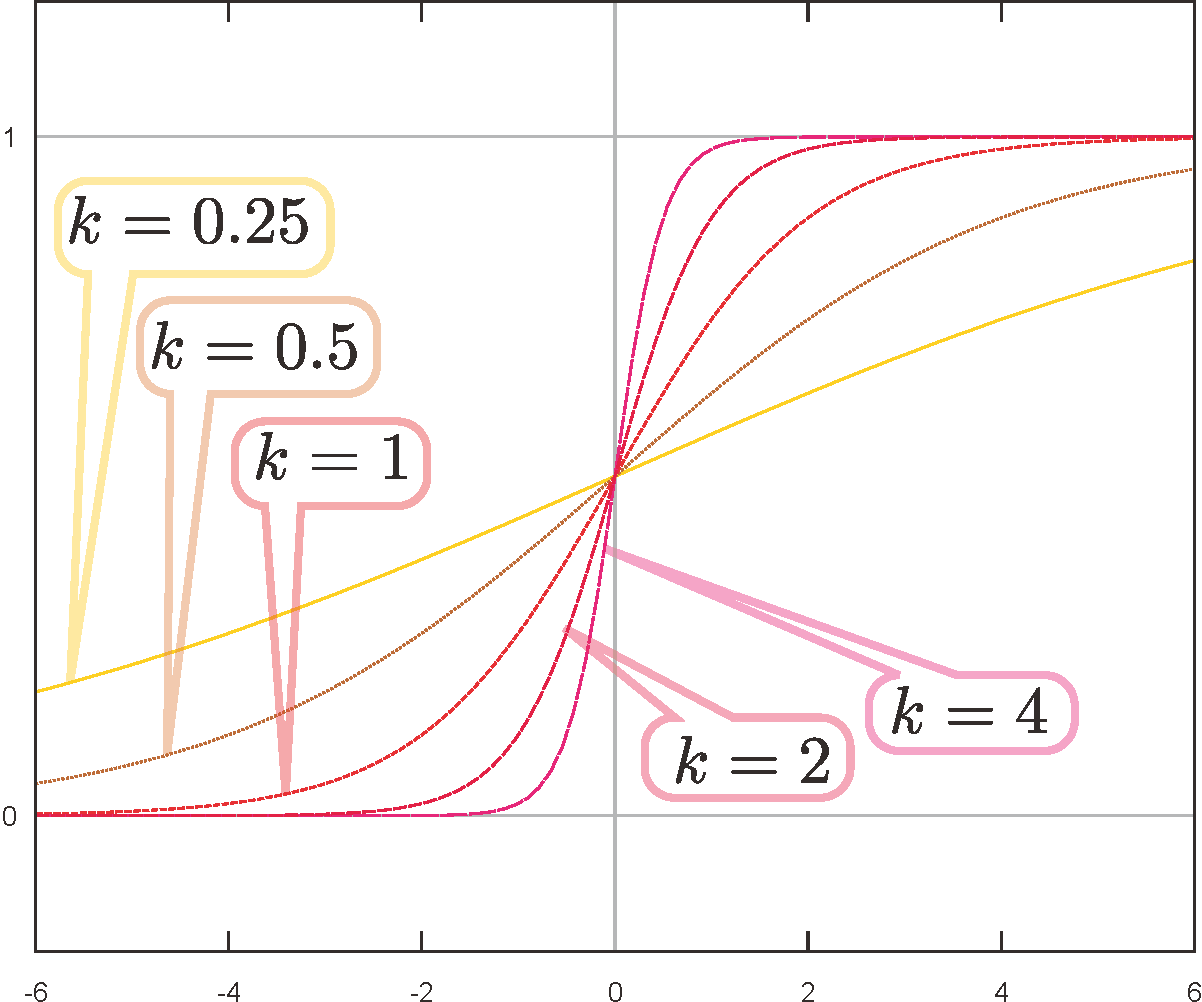
途中で複号$\pm$をつけたが、これは${\ycol{y}\over 1-\ycol{y}}$が正のとき$+$、負のとき$-$である。よって本来解こうとしていた問題においては$+$をとっておけばよい(グラフもそうしている)。
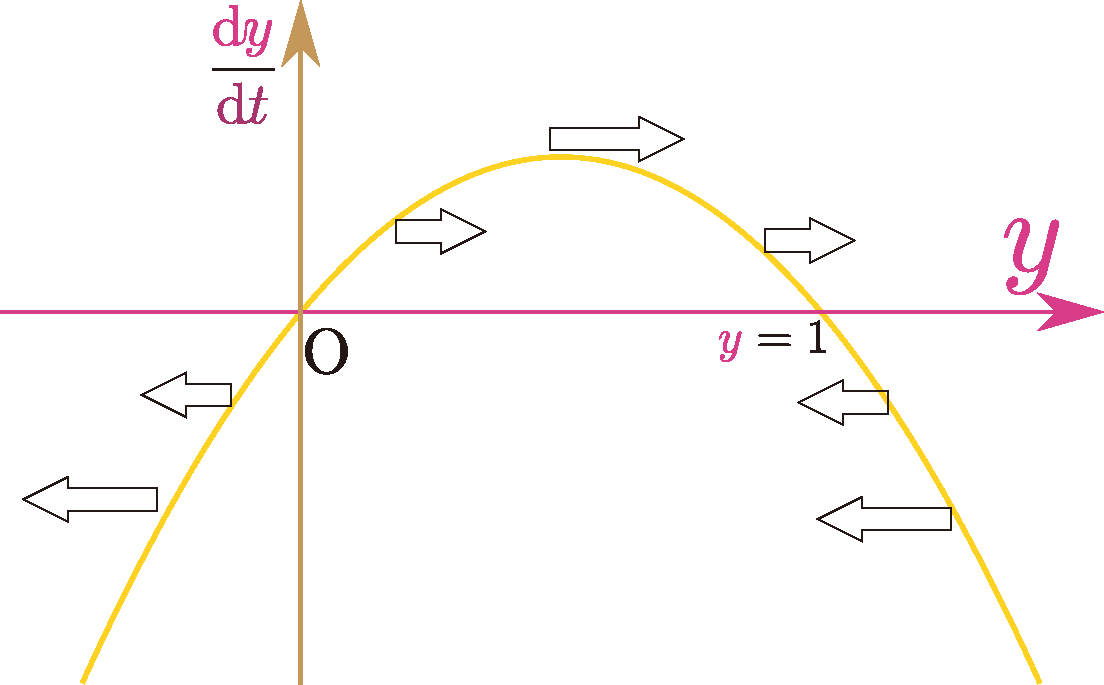
上のグラフが$ {\coldy\over \coldt}=k\ycol{y}(1-\ycol{y})$のグラフである。${\coldy\over \coldt}$は$\ycol{y}=0$と$\ycol{y}=1$で0となり、その間の範囲で正、それ以外の場所で負である。よって時間経過した時の変化を考えると、$0<\ycol{y}<1$では増加し、それ以外では減少する。結果として$\ycol{y}$の値は$\ycol{y}=1$へと集まっていく(そして、$\ycol{y}=0$からは離れていく)という傾向を示す。
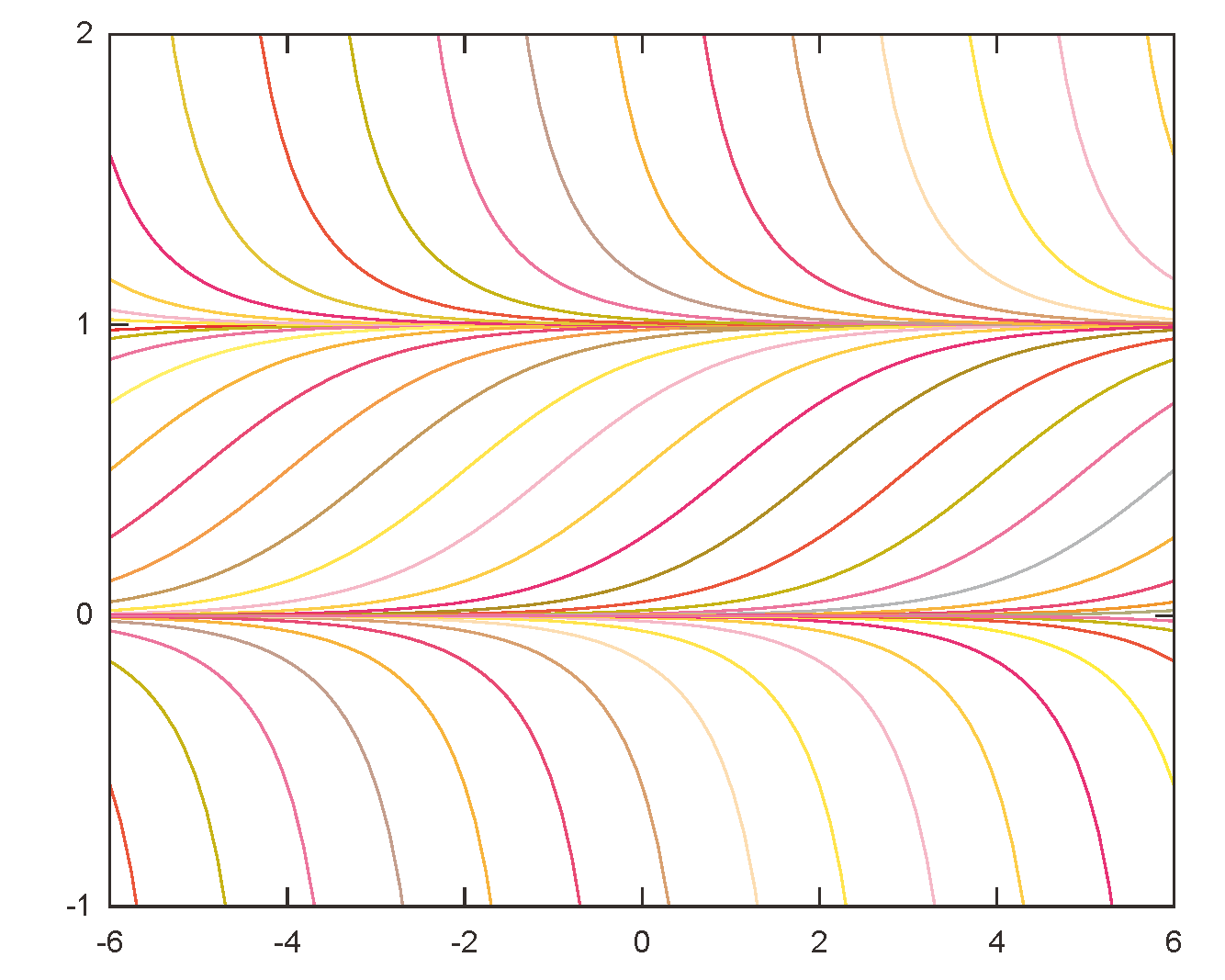
$\ycol{y}$の範囲を拡大して、1より大きい場合や0より小さい場合も含めてどのような関数になっているかを示したのが上の図である。この場合$\ycol{y}<0$のとき、$\ycol{y}>1$のときは${\ycol{y}\over 1-\ycol{y}}$が負になるので、解として$\ycol{y}={1\over 1-\E^{-k \tcol{t}-C}}$(複号がマイナスの方)を取る。解曲線全体を見ると、$\ycol{y}=0$から離れていき、$\ycol{y}=1$に引き寄せられていることがわかる。
今求まった$\ycol{y}={1\over 1\pm\E^{-k \tcol{t}-C}}$という解には実は「抜け」がある。$\ycol{y}=0$と$\ycol{y}=1$(定数で、このままずっと変化しない)というのも、もともとの微分方程式\式{ryukouone}の解であるが、それは今求めた解の複号$\pm$と積分定数$C$の値をどう決めても出てこない。今求めた解は非常に微妙なところで「一般解」になり損なっている。
「抜け」の原因は式変形において両辺を$\ycol{y}(1-\ycol{y})$で割ったことである。割算では、割る数が0でないかを確認しなくてはいけない。つまり$\ycol{y}(1-\ycol{y})$で割ったことにより、その後の式は$\ycol{y}(1-\ycol{y})\neq0$の場合に限る話になっている。$\ycol{y}(1-\ycol{y})=0$の場合は別に考慮しなくてはいけない。それが解になってないならその可能性を捨てればよいのだが、この場合はこれらも解になる。$\ycol{y}$が一定になる場合は右辺も左辺$\left({\coldy\over \coldt}\right)$も0になるからである。この二つ$\ycol{y}=0$と$\ycol{y}=1$は今求めた解$\ycol{y}={1\over 1\pm\E^{-k \tcol{t}-C}}$に含まれない解となる。このような解を「特異解(singular solution)」と呼ぶ。
今の場合の(文字通りの)一般解は以下の通りである。 \begin{equation} \ycol{y}={1\over 1\pm\E^{-k \tcol{t}-C}}(Cは任意定数)~~または~~\ycol{y}=0~~または~~\ycol{y}=1 \end{equation}