パラボラアンテナ

$\def\coldr{\rcol{\mathrm dr}}\def\coldvecx{\xcol{\mathrm d\vec x}}\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{~~~~~~~{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}\def\kidy{\opcol{\diff y}}\def\ve{\vec{\mathbf e}}\def\colvecx{\xcol{\vec x}}\definecolor{usuopcolor}{RGB}{237,234,203}\def\usuopcol#1{\color{usuopcolor}#1}\def\vgrad#1{{\usuopcol{\overrightarrow{\opcol{\rm grad}~\kuro{#1}}}}}\def\dX{\rcol{\mathrm dX}}\def\dY{\thetacol{\mathrm dY}}\def\opdf{\opcol{\mathrm df}}\def\coldf{\tcol{\mathrm df}}\def\dtwof{\opcol{\mathrm d^2f}}\def\murasakidb{\zcol{\mathrm d b}}\def\ao{\ycol}\def\aodV{\ycol{\diff V}}\def\aka{\xcol}\def\akadm{\xcol{\diff m}}\def\gunderbrace{\underbrace}$

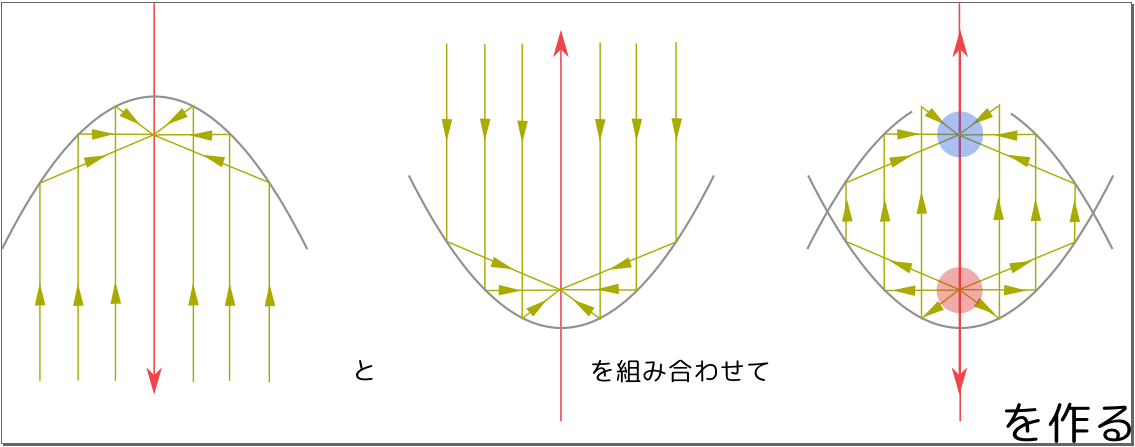
　このおもちゃと同じ原理が衛星放送などの受信アンテナに使われている。アンテナは遠方からやってきたほぼ平行な電波を反射させ、一点（焦点）に集める。${x}$軸正方向からきた平行光線を原点に集めるようにするためには、鏡をどのような形に並べればよいか？---これを求めようとすると、微分方程式の手助けが必要になってくる。

　下の図のように$\xcol{x}$軸の正の方向から電波もしくは光が入射してきて、曲面の鏡に反射した後O点に集まる、という状況を考えよう。

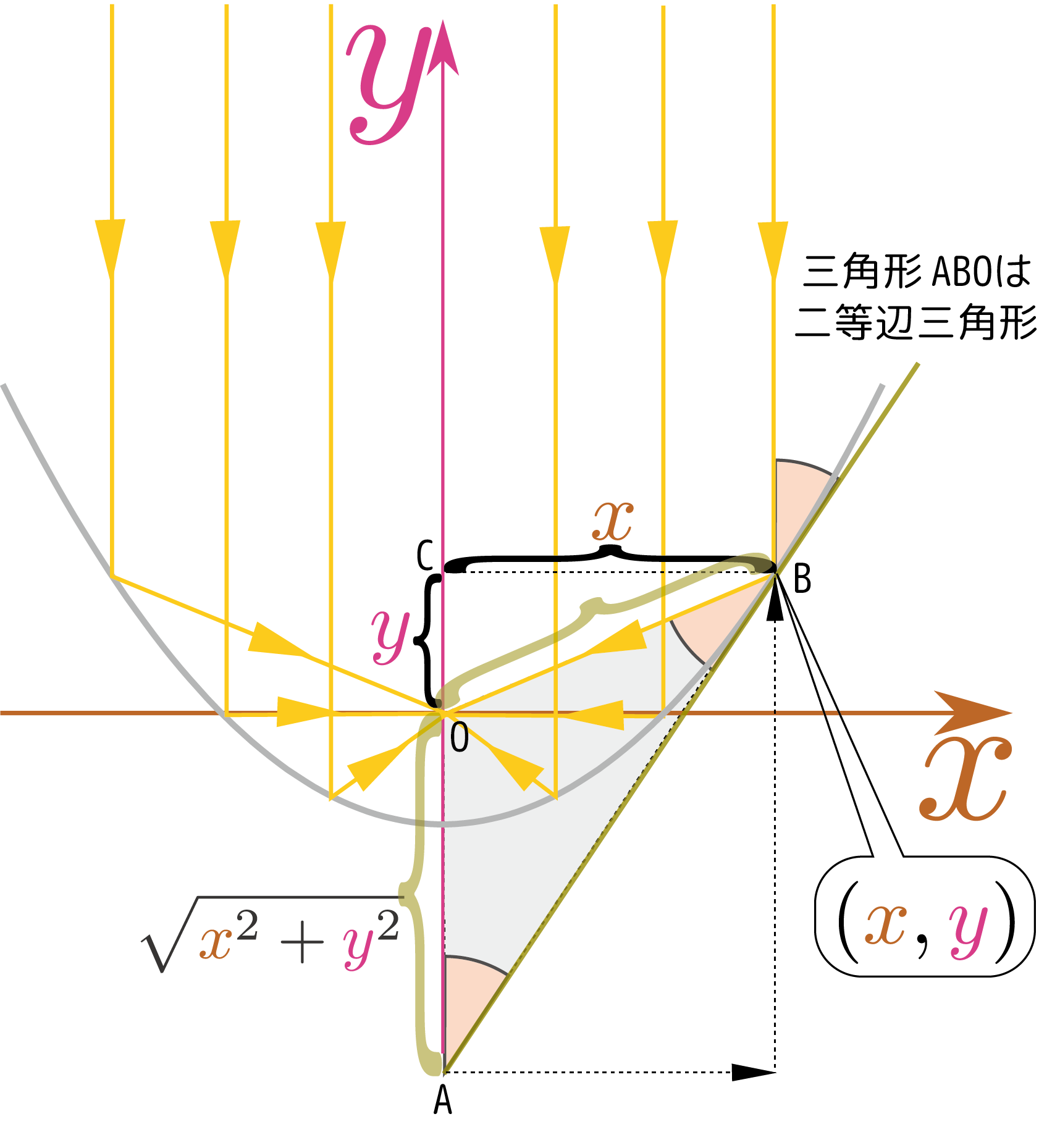
　点Bで反射した光がOに向かうためには、鏡の反射の性質（入射光と反射光の鏡面に対する角度が等しい）から、図の$\angle$BAOと$\angle$ABO（ここで、AはBにおける接線が$\ycol{y}$軸と交わる点である）が等しくならなくてはいけない。よって図の三角形ABOは二等辺三角形であり、AO=BO=$\sqrt{\xcol{x}^2+\ycol{y}^2}$と書くことができる。以上から図に描き込んだように各部の長さを求めていく。「AからBに行くには、右に$\xcol{x}$、上に$\ycol{y}+\sqrt{\xcol{x}^2+\ycol{y}^2}$だけ移動すればよい」と考えると、点Bにおける接線の傾き$\left({\coldy\over \coldx}\right)$が \begin{equation} {\coldy\over \coldx}={\xcol{y}+\sqrt{\xcol{x}^2+\ycol{y}^2}\over \xcol{x}} \end{equation} であることがわかり、これが曲線を求めるための微分方程式となる。この式は同次方程式だから \begin{equation} {\coldy\over \coldx}={\ycol{y}\over \xcol{x}}+\sqrt{\left({\ycol{y}\over \xcol{x}}\right)^2+1} \end{equation} と直し、$\zcol{z}={\ycol{y}\over \xcol{x}}$を変数とした方がよい。

$\ycol{y}=\zcol{z}\xcol{x}$としてから微分すると$\coldy = \coldz\xcol{x}+\zcol{z}\coldx$という関係式が出るので、 \begin{equation} \begin{array}{rl} \xcol{x} {\coldz\over \coldx}+{\zcol{z}}=&{\zcol{z}}+\sqrt{\zcol{z}^2+1}\\ \end{array} \end{equation} となって（両辺の$\zcol{z}$は消えて）後はこれを変数分離した${\coldz\over \sqrt{\zcol{z}^2+1}}={\coldx \over \xcol{x}}$を積分すればよい。

　$\sqrt{\zcol{z}^2+1}$が出てきた時の定番$\sqrt{\zcol{z}^2+1}$が簡単になるような$\zcol{z}$は何か？---と考えていけば、$\sqrt{\sinh^2 \tcol{t}+1}=\cosh \tcol{t}$というのがあったな、と思いつく。「こんなの、思いつけない」と思っても悲観する必要はない。別に天才的ひらめきで見つけたりするものではなく、「これはどうかな？」という試行錯誤（当然何度か失敗する）と「前にも似たようなの出てきたな」という慣れで見つけるものである。慣れてない最初はとにかくいろいろ試して、うまくいく方法を探そう。として、$\zcol{z}=\sinh \tcol{t}$と置く。

　なお、この「定番」よりも有名な定番は$\sqrt{1-x^2}$が出てきたときの$x=\sin\theta$である。このときは$\mathrm dx=\cos\theta\mathrm d\theta$となるが、$\sqrt{1-x^2}=\cos\theta$であるおかげで$\sqrt{1-x^2}$が消えてくれた。これに似た（ただし符号が違う）関数として$\sinh t$を持ってくる。

　こうして$\sqrt{\zcol{z}^2+1}=\sqrt{1+\sinh^2 \tcol{t}}=\cosh \tcol{t}$、$\coldz=\cosh \tcol{t} \coldt$と置き換えられて、 \begin{equation} \begin{array}{rl} \int \coldt =& \int {\coldx\over \xcol{x}}\\[3mm] \tcol{t}=& \log \xcol{x}+C\\ \end{array} \end{equation} と積分ができる。$\zcol{z}=\sinh \tcol{t}={\E^{\tcol{t}}-\E^{-\tcol{t}}\over 2}$に上で求めた式からわかる$\E^{\tcol{t}}=\E^C \xcol{x}$を代入し、 \begin{equation} \begin{array}{rll} \zcol{z}=& {\E^C \xcol{x}-{1\over \E^C\xcol{x}}\over 2}&\kokode{両辺に\xcol{x}を掛けて}\\ \underbrace{\zcol{z}\xcol{x}}_{\ycol{y}}=& {\E^C\xcol{x}^2-{1\over \E^C}\over 2}\\ \end{array} \end{equation} と答えを出す。未定のパラメータである$\E^C$を$\E^C=2k$（$k$は正の定数）と書きなおして \begin{equation} \ycol{y}=k{\xcol{x}}^2 - {1\over 4k} \end{equation} というのが答である。途中の積分が面倒な割には、答は放物線である。ちなみに「パラボラアンテナ」の「パラボラ」とは放物線のことである実際に衛星放送のアンテナなどに使われている曲面は放物線を回転させた面の一部であり、図に描き込んであるようにアンテナの中心と放物線の軸はずらしてある。。

懸垂線

紐を２点を固定してつりさげた時の形を考えてみる。どんな形になるだろう？？

　うん、そう思う人が多い。というわけで、プロジェクタで写した$y=x^2$のグラフと鎖を垂らしたものを重ねてみたのが、

である。微妙に、合わない。一方、$y=\cosh x$で重ねてみたのが、

で、実に見事に一致している。

　一番下の部分を原点として、次の図のように座標系を張る。

　紐にかかる張力は（垂直に垂らした時と同様に、上の方ほど大きくなるはずだから、図のように微小部分を考えた時、下端には$\tcol{T}$、上端には$\tcol{T}+\tcol{\mathrm dT}$の力が働く。紐は直線状ではないからこの張力の向きも（微小に）違う。働く力はこの他に重力がある。微小部分の紐の長さは$\sqrt{\coldx^2+\coldy^2}$だから、これに単位長さあたりの質量$\rho$と重力加速度$g$を掛けた分の重力が下向きに働く。

　上の図を参考に、$\tcol{T}$を鉛直成分と水平成分に分ける（その比は$\coldy:\coldx$）。この微小部分に働く張力の水平成分は等しいはずである。よって、 \begin{equation} \diff \goverbrace{\left( \tcol{T}{\coldx\over \sqrt{\coldx^2+\coldy^2}} \right)}^{Tの水平成分}=0 \end{equation} あるいは \begin{equation} \tcol{T}{\coldx\over \sqrt{\coldx^2+\coldy^2}}=T_0~~~(T_0は定数)\label{suiheiteisuu} \end{equation} が成り立つ。ここで$T_0$は、$\coldy=0$の時の張力だと思えばよい（図を見ると、それは最下点すなわち原点である）。

　次に鉛直成分を考えると、$\tcol{T}$の鉛直成分の増加がちょうど重力によって打ち消されればつりあいが保たれるから、「$\tcol{T}$の鉛直成分の微小変化」が、その微小部分にかかる重力に等しくなり、 \begin{equation} \diff\goverbrace{ \left( \tcol{T}{\coldy\over \sqrt{\coldx^2+\coldy^2}} \right)}^{Tの鉛直成分}=\rho g \sqrt{\coldx^2+\coldy^2} \end{equation} が成り立つ。

　$\tcol{T}=T_0{\sqrt{\coldx^2+\coldy^2}\over \coldx}$となるからこれを代入すれば \begin{equation} \diff \left( T_0{\coldy\over \coldx} \right)=\rho g \sqrt{\coldx^2+\coldy^2} \end{equation} となる。$T_0$は定数だから微分の外に出して、右辺は$\coldx$をルートの外に出し、 \begin{equation} T_0\diff \left({\coldy\over \coldx}\right)=\rho g\sqrt{1+\left({\coldy\over \coldx}\right)^2}\coldx \end{equation} とした上で、${\coldy\over \coldx}=\ycol{V}$と考えれば \begin{equation} T_0\ycol{\mathrm dV}= {\rho g}\sqrt{1+\ycol{V}^2}\coldx\label{Vrhog} \end{equation} という変数分離可能な微分方程式になる。$\sqrt{1+\ycol{V}^2}$という形が出てきたので、前節同様、$\ycol{V}=\sinh \tcol{t}$という置換積分（$\ycol{\mathrm dV}=\cosh \tcol{t} \coldt$となる）を使って計算して、 \begin{equation} \begin{array}{rll} {\ycol{\mathrm dV}\over \sqrt{1+\ycol{V}^2}}=&{\rho g\over T_0}\coldx &\kokode{\kuro{\ycol{V}=\sinh \tcol{t}}として} \\ {\cosh \tcol{t} \coldt\over \cosh \tcol{t}}=&{\rho g\over T_0}\coldx &\kokode{積分して} \\ \tcol{t}=&{\rho g\over T_0}\xcol{x}+C~~~&(Cは積分定数) \end{array} \end{equation} であるから、 \begin{equation} \ycol{V}={\coldy\over \coldx}= \sinh \left({\rho g\over T_0}\xcol{x}+C\right) \end{equation} となる。これをさらに積分して、 \begin{equation} \ycol{y}= {T_0\over \rho g}\cosh \kakko{{\rho g\over T_0}\xcol{x}+C}+D~~~(Dは積分定数) \end{equation} が解となる。最初に図で設定したように$\xcol{x}=0$で$\ycol{y}=0,{\coldy\over \coldx}=0$とすれば、$C=0,D={-{T_0\over \rho g}}$となり（$C,D$を変えると最下点が移動することになる）、最終的な答えは \begin{equation} \ycol{y}= {T_0\over \rho g}\left( \cosh \kakko{{\rho g\over T_0}\xcol{x}}-1\right)\label{kensui} \end{equation} となる。

　このような曲線（$\cosh$で表される）を「懸垂線」と呼ぶ。

弱肉強食の微分方程式

兎と狐の増減

　ある森の中で草食動物（兎）の数$\rcol{X}$と肉食動物（狐）の数$\thetacol{Y}$がどう増減するかを考える（簡単のため、この森にはこの2種類の動物しかいないものとする）。

　餌が豊富にあり、かつ狐がいないと考えた場合、兎は今いる量に比例して増えると同時に寿命が来て死ぬ分減る（減る量も今いる量に比例する）。この二つの効果のみを考えるならば、 \begin{equation} \opcol{\diff\rcol{X}\over \kidt}= A\rcol{X}\label{lwonezero} \end{equation} という微分方程式で兎の数$\rcol{X}$の変化が記述できそうである。ただし$A$は比例定数で兎は自然には増えるということを反映して、正の定数となる。

　ところが兎が減る原因はもう一つある。狐は兎を食べるので、兎は狐と出会うと死ぬと考えよう。森の中に$\rcol{X}$匹の兎と$\thetacol{Y}$匹の狐がそれぞれ動きまわっている状況を考えると、両者が出会う確率は$\rcol{X}$と$\thetacol{Y}$の積に比例するだろう。そして出会った後でやはりある確率で「狐が兎を食べる」というイベントが発生し、兎が減る。このように考えると、兎の減少量として$\rcol{X}\thetacol{Y}$という積に比例する部分が出てくる。よって、兎の数は \begin{equation} \opcol{\diff\rcol{X}\over \kidt}= A\rcol{X} -B\rcol{X}\thetacol{Y}\label{lwone} \end{equation} という式で増減するとする（$B$は$A$とは別の比例定数）。

　一方狐は、兎を食べないと生きていけないのだから、その増加はどれだけ兎を食べられるかによって決まり、それは$\rcol{X}\thetacol{Y}$に比例するのだったから、狐は$\rcol{X}\thetacol{Y}$に比例して増える。兎がいなかったら狐は「繁殖しつつ寿命が来て死ぬ」という現象の結果として現在いる量に比例して減っていくだろう。それを$-C\thetacol{Y}$という形（$C$は正の定数、ほっておくと増える兎とは符号が逆になる）で式の右辺に入れて、 \begin{equation} \opcol{\diff\thetacol{Y}\over \kidt}= -C \thetacol{Y} + D \rcol{X}\thetacol{Y}\label{lwtwo} \end{equation} という微分方程式に従う（$C,D$は$A,B$とは別の比例定数である）。これらの方程式はこの式を出した二人の数学者の名前を取って「ロトカ・ヴォルテラの方程式」と呼ばれる。

　時間変化を考えるには、$\opcol{\diff \rcol{X}\over \kidt},\opcol{\diff\thetacol{Y}\over \kidt}$に関する二つの微分方程式を連立させて解けばよい。

　いきなり解けと言われても、どうしていいのか悩んでしまうかもしれない（この式は非線形だし）。そこでまず、「$\opcol{\diff \rcol{X}\over \kidt}=\opcol{\diff\thetacol{Y}\over \kidt}=0$となるのはどんなときか？」から考える。$\opcol{\diff \rcol{X}\over \kidt}=\opcol{\diff\thetacol{Y}\over \kidt}=0$となる点を「固定点」と呼ぶ。

　固定点を求める方程式は上の微分方程式の右辺が$0$になる、という式で、因数分解すれば \begin{eqnarray} \rcol{X}(A-B\thetacol{Y})&=&0\\ \thetacol{Y}(-C+D\rcol{X})&=&0 \end{eqnarray} である。$\rcol{X}=\thetacol{Y}=0$もこの方程式の解だが、「兎も狐もいない」という「つまらない解」最初から兎も狐もいないのだから、未来永劫いないままである。なので無視する。

　$\rcol{X}={C\over D},\thetacol{Y}={A\over B}$が意味のある固定点である。

　固定点からのずれを$\xcol{x},\ycol{y}$とする。つまり、 \begin{equation} \rcol{X}= {C\over D}+\xcol{x},~~\thetacol{Y}={A\over B}+\ycol{y} \end{equation} とする。こうして$\xcol{x},\ycol{y}$の微分方程式を作ると、 \begin{equation} {\coldx\over \coldt}= -B \left({C\over D}+\xcol{x}\right) \ycol{y},~~~ {\coldy \over \coldt}= D\left({A\over B}+\ycol{y}\right)\xcol{x} \end{equation} となる。ここで$\xcol{x},\ycol{y}$は${C\over D},{A\over B}$に比べて小さいと考えて、括弧内の$\xcol{x},\ycol{y}$は無視して、 \begin{equation} {\coldx\over \coldt}= -{BC\over D} \ycol{y},~~~ {\coldy \over \coldt}= {AD\over B} \xcol{x} \end{equation} と近似する。

　この式を見ながら固定点からずれた時の$\opcol{\diff\rcol{X}\over\kidt},\opcol{\diff \thetacol{Y}\over\kidt}$の様子を予想してグラフに表示すると次のようになる。

　$\rcol{X},\thetacol{Y}$の時間変化を表すのが次のグラフである。

　グラフに示したように、狐のグラフが「山」である間は兎のグラフは右下がり、狐のグラフが「谷」である間は兎のグラフが右上がりとなる。もちろんこれは「狐が多くて兎が食われる時期は兎が減り、狐が少なくなると兎が増える」を示している。逆に「兎が多いと狐が増える（およびこの逆）」もわかる。グラフを見ながらそれを確認してみよう。

　ここまでで求めたのは近似解なので、$\rcol{X}$-$\thetacol{Y}$平面に描かれる図形は単純な楕円であるが、実際に微分方程式を解いてみると少々複雑な図形を描く。動くグラフはにある。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。