多変数関数

　1変数の場合の「関数」とは、「独立変数であるある量$A$を決めると、従属変数であるある量$B$が決まる」という対応関係であった。 独立変数が一つの量ではなくなり、

　複数の独立変数であるある一組の量$A_1,A_2,\ldots$を決めると、従属変数であるある量$B$が決まる。

という対応関係もちろん、\ycol{\ovalbox{ある量$B$}}はただひとつに定まらなくてはいけない。となったものを「多変数関数(multivariable function)」と呼ぶこの「多」は「独立変数が複数」という意味である。。$\xcol{x},\ycol{y}$を決めると$\zcol{z}$が決まる、という対応関係なら、$\zcol{z}=f\kakko{\xcol{x},\ycol{y}}$のように書く（この場合は「2変数関数」）。たとえば$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}\ycol{y},f\kakko{\xcol{x},\ycol{y}}=\xcol{x}+\ycol{y},f\kakko{\xcol{x},\ycol{y}}=\E^{\xcol{x}}\cos \ycol{y},\ldots$などがある。

　1変数の関数は、独立変数と従属変数という二つの変数を持っているが、独立変数一つを決めれば従属変数も決まったから「自由に動かせる数」は一つであった。

　この「自由に動かせる数が一つ」であることを自由度(degree of freedom)が1、と表現する。2変数の関数の場合、二つの独立変数を決めると従属変数が決まるから、自由度は2である（3変数、4変数と増えていっても同様である）。

　現実的な問題では複数の（2どころか3や4やもっと多くの）独立変数を持っている場合がほとんどたとえば「各地の気温」の独立変数は地点を表す緯度・経度の二つだから、多変数関数を使えないと天気予報もできない。であるから、多変数関数を自由に使えるようになってこそ、「使える数学」になる。

　１変数の関数の例としては、一辺$\xcol{x}$の正方形の面積 $$ \rcol{S}=\xcol{x}^2 $$ がある。この量の微小変化を考えて、 $$ \rcol{\diff S}=2\xcol{x}\coldx $$ のように二つの微小変化の関係を求めるのが「微分」という計算である。

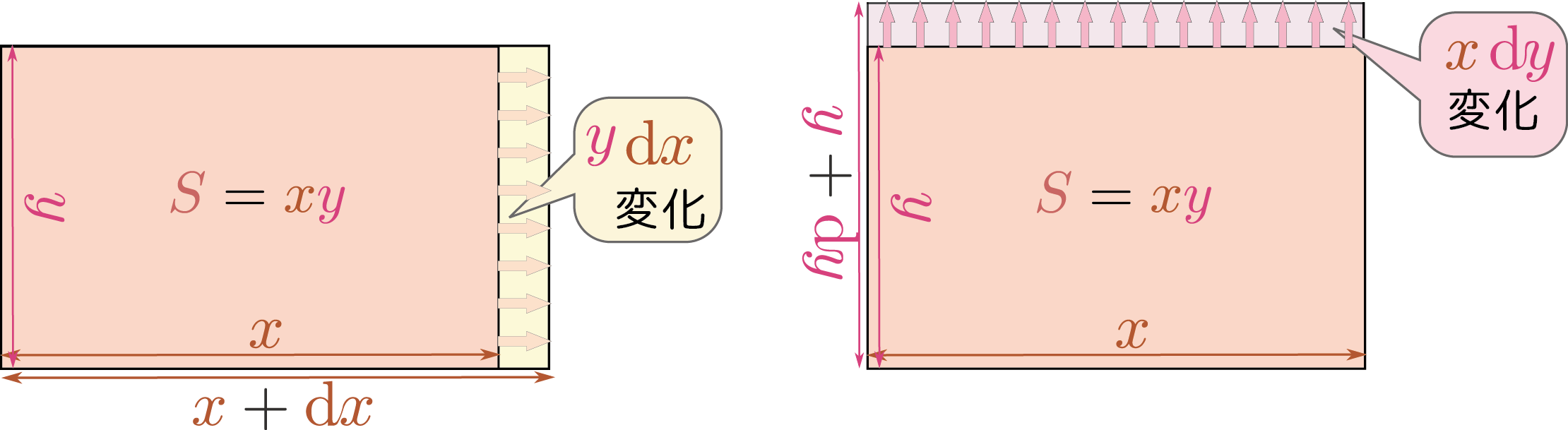
　２変数関数の例として横が$\xcol{x}$、縦が$\ycol{y}$の長方形の面積$\rcol{S}=\xcol{x}\ycol{y}$を考えると、これの微分については、 \begin{equation} \rcol{\diff S}=\ycol{y}\coldx+ \xcol{x}\coldy \end{equation} という式が成立する。これは$\rcol{S}=\xcol{x}\ycol{y}$を\reftext{Leibniz}{ライプニッツ則}にしたがって \begin{equation} \rcol{\diff S}=\gunderbrace{\coldx \ycol{y}}_{\xcol{x}を微分した項}+ \gunderbrace{\xcol{x}\coldy}_{\ycol{y}を微分した項} \end{equation} のように微分したと考えても、 \begin{equation} \goverbrace{ \left(\xcol{x}+\coldx\right) \left(\ycol{y}+\coldy\right)}^{変化後}-\goverbrace{\xcol{x}\ycol{y}}^{変化前}=\ycol{y}\coldx+ \xcol{x}\coldy+\gunderbrace{\coldx\coldy}_{高次の微小量} \end{equation} のように変化後ー変化前と引算して高次の微小量を無視して求めても、すべて同じ結果となる。

　下の図のように考えて「$\xcol{x}$が$\coldx$変化したときには$\rcol{S}$が$\ycol{y}\coldx$だけ変化する」と「$\ycol{y}$が$\coldy$変化したときには$\rcol{S}$が$\xcol{x}\coldy$だけ変化する」としてもよい。

円柱の体積$\thetacol{V}=\pi\rcol{r}^2\xcol{h}$

　高さ$\xcol{h}$を$\xcol{\diff h}$変化させたとすると、その変化による体積の変化は$\pi\rcol{r}^2 \xcol{\mathrm dh}$である。半径が$\coldr$変化する場合の体積変化は$2\pi \rcol{r}\xcol{h}\coldr$となる。

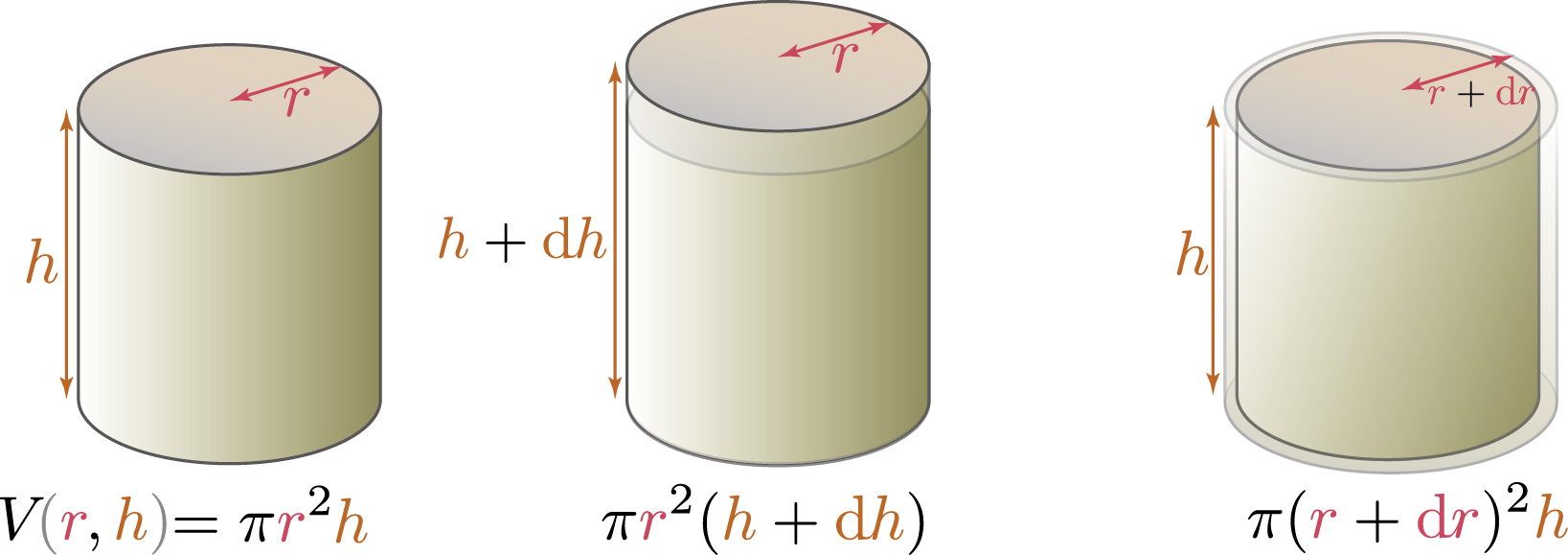
　この二つの量（$\pi\rcol{r}^2 \xcol{\mathrm dh}$と$2\pi \rcol{r}\xcol{h}\coldr$）は、上の図に示した体積増加部分であるが、微分を使って数式で表現すれば、 \begin{equation} \thetacol{\mathrm dV}\kakko{\rcol{r},\xcol{h}} = \pi \rcol{r}^2\xcol{\mathrm dh} + 2\pi\rcol{r}\xcol{h}\coldr\label{enchuuhenbibun} \end{equation} となる。二つの係数がそれぞれ底面積（図では「天井の面積」として描いているが）と側面積という意味を持っていることに注意しよう。

　以上のように、2変数関数では少なくとも二種類の変化を考える必要がある実は二つの変化の線形結合により任意の方向すべての変化が考えられる（これについては後で考える）。。

平面上の距離$\rcol{R}=\sqrt{\xcol{x}^2+\ycol{y}^2}$

　原点から点$(\xcol{x},\ycol{y})$までの距離$f\kakko{\xcol{x},\ycol{y}}=\sqrt{\xcol{x}^2+\ycol{y}^2}$の微小変化を考えると、 \begin{equation} \diff \left(\sqrt{\xcol{x}^2+\ycol{y}^2}\right)= {\xcol{x}\over\sqrt{\xcol{x}^2+\ycol{y}^2} }\coldx +{\ycol{y}\over\sqrt{\xcol{x}^2+\ycol{y}^2} }\coldy\label{Rzenbibun} \end{equation} である。この式は以下に示す二つの方法で確認することができる。

　まず、図を描いて変化の様子を考えると、次のようになる。

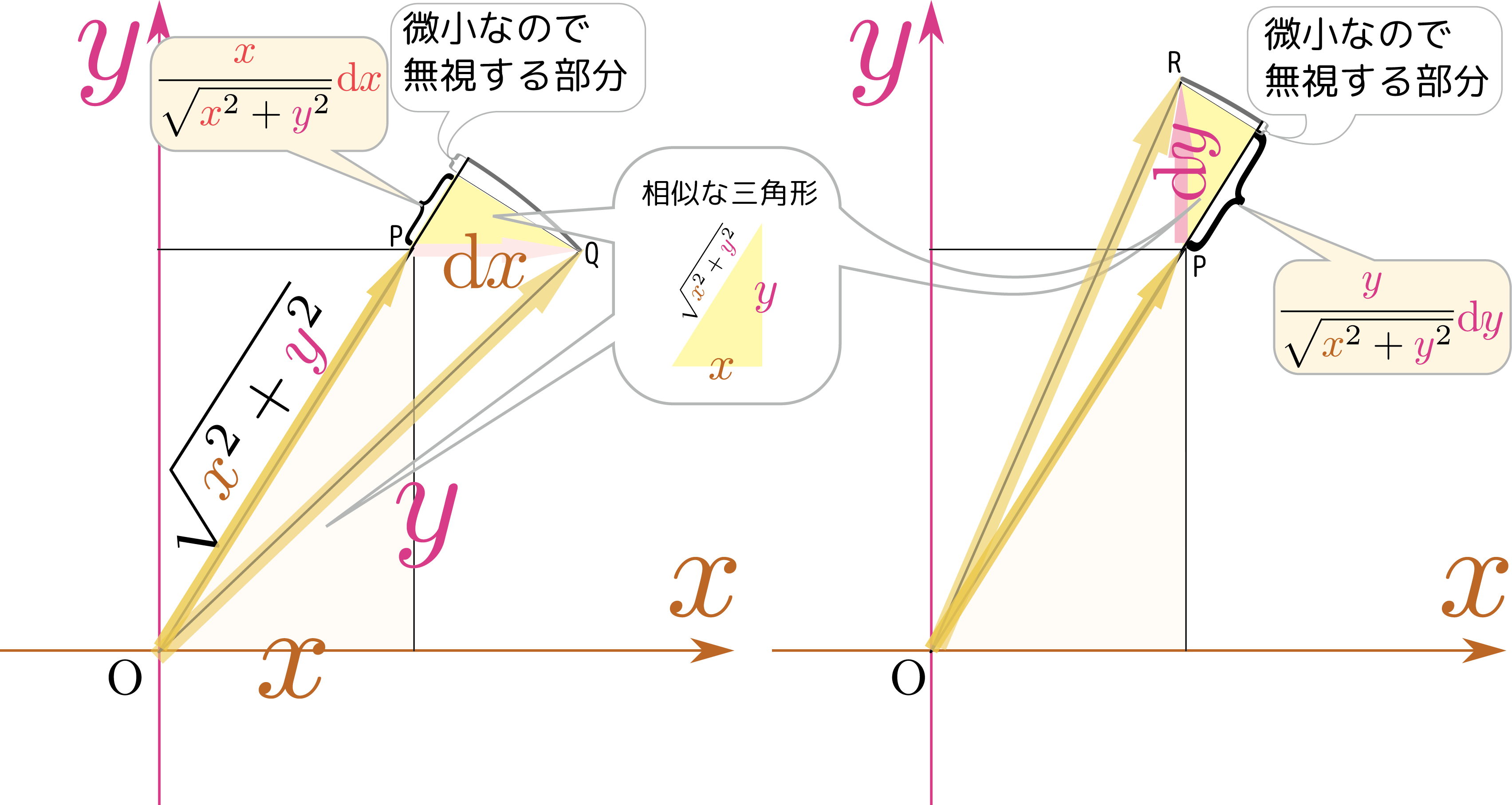
　上の図の左のグラフには、（$\ycol{y}$を変えずに）$\xcol{x}$を$\coldx$だけ増加させたときの距離の変化（図に｛で示した部分）を描いた。三角形の相似から、この距離が${\xcol{x}\over\sqrt{\xcol{x}^2+\ycol{y}^2} }\coldx$である。上の図の右のグラフには（$\xcol{x}$を変えずに）$\ycol{y}$を$\coldy$だけ変化させた場合の距離の変化（図で｝で示した部分）を描いている。これも三角形の相似から${\ycol{y}\over\sqrt{\xcol{x}^2+\ycol{y}^2} }\coldy$である。

　この式を得るもう一つの方法は、数式を微分することである。たとえば${\xcol{x}\over\sqrt{\xcol{x}^2+\ycol{y}^2} }$は$\sqrt{\xcol{x}^2+\ycol{y}^2}$を、\文中式{$\ycol{y}$は変化しないものとして、$\xcol{x}$で微分}することで得られる。$\ycol{y}$が変数であることを一旦忘れて（なんなら$\sqrt{\xcol{x}^2+C^2}$のように定数$C$に置き直して考えて）、普通に$\xcol{x}$で微分という操作を行えばよい。

　${\ycol{y}\over\sqrt{\xcol{x}^2+\ycol{y}^2} }$は$\xcol{x}$と$\ycol{y}$の立場が入れ替わっただけで、同様である。

偏微分の定義と記号

　この新しい形式の微分に名前と定義と、そして新しい記号を与えよう新しい記号が出て来ると「ああ、難しい話が始まった」とその記号を使うことに心理的拒否反応を示す人が時々いるのだが、この「新しい形式の微分」はこれまでも無意識に使っていたはずである。以下は、それに新しい名前をつけようというだけのことであるから、難しく考え過ぎないように。。

　上で述べたような「複数個ある変数のうち一つの変数の変化だけに着目して微分する」微分を「\newwordE{へんびぶん}{偏微分}{partial differential}」と呼ぶ。名前の通り「肉と野菜を出されたのに、偏食して、肉しか食べない」というときの「偏」である。partialは「一部だけ」を意味している。「偏りのある微分」で、変数が二つ（ときには、三つ以上）あるのに、その変数のうち一個だけの変化を考え、それ以外の変数は「変化しないもの」と（あたかも定数であるかのように）扱って微分を行う。

　常微分の表現として、$f\kakko{\xcol{x}+\coldx}=f\kakko{\xcol{x}}+{\mathrm df\over\diff x}\kakko{\xcol{x}}\coldx$もしくは、$\mathrm df={\mathrm df\over\diff x}\kakko{\xcol{x}}\coldx$という書き方具体例で示せば、$\cos\kakko{\xcol{x}+\coldx}=\cos \xcol{x}-\sin\xcol{x}\coldx$もしくは$\diff (\cos\xcol{x})=-\sin\xcol{x}\coldx$など。があった。「独立変数$\xcol{x}$が$\coldx$だけ変化すると、関数$f\kakko{\xcol{x}}$が${\mathrm df\over\diff x}\kakko{\xcol{x}}\coldx$だけ変化する」というのがこの書き方の意味するところである。つまり微係数${\mathrm df\over\diff x}\kakko{\xcol{x}}$とは「独立変数$\xcol{x}$の微小変化と関数$f\kakko{\xcol{x}}$の微小変化の比」にあたる数である。なお、「比」と書いたが単純に割算すればいいかというとそうではない。$\coldx\to0$という極限を取ることで計算される量なので、「$\coldx$の高次の項は無視する」などの手順が必要である。

　2変数関数では独立変数が$\xcol{x},\ycol{y}$と二つあるので「$\xcol{x}$の微小変化と$f\kakko{\xcol{x},\ycol{y}}$の微小変化の比」と「$\ycol{y}$の微小変化と$f\kakko{\xcol{x},\ycol{y}}$の微小変化の比」を両方考えなくてはいけない。つまり微係数は${\mathrm df\over \diff x}$の一つでは済まなくなる。二つの微係数を$\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}$と$\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}$という記号（記号のそれぞれの意味はすぐ後で述べる）を使って、 \begin{equation} f\kakko{\xcol{x}+\coldx,\ycol{y}+\coldy} =f\kakko{\xcol{x},\ycol{y}}+ \PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}\coldx +\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}\coldy\label{defhenbibun} \end{equation} もしくは \begin{equation} \mathrm df\kakko{\xcol{x},\ycol{y}}=\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}\coldx +\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}\coldy \label{zenbibun} \end{equation} と書く。常微分における「導関数」または「微係数」にあたるもの（上の$\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}$と$\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}$など）を、「\newwordE{へんどうかんすう}{偏導関数}{partial derivative}」または「偏微係数（偏微分係数）」と呼ぼう。偏導関数を求める計算が「偏微分」である。

　偏微分では$\diff$ではなく$\partial$という記号を使い、かつ、$\opcol{\left(~~\right)}_{\!\ycol{y}}$のように括弧の後に「（本当は変数なんだけど）変化させていない変数」を下付き添字の形でつけて表現する。誤解が起こらないだろうと思われるときは省略され関数の引数が$\kakko{\xcol{x},\ycol{y}}$だから、$\xcol{x}$で微分するなら$\ycol{y}$が一定なのは当然でしょ、という考え方をする。、単に$\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}$と書く場合も多いさらに$\PD{f}{\xcol{x}}$のように関数の引数も省略されている場合もあるが、その場合は文脈を読んで判断することになる（文脈から判断しにくい場合は省略すべきではない）。。$\PD{f\kakko{\xcol{x},\ycol{y}}}{{\xcol{x}}}\biggr|_{\ycol{y}}$のように、偏微分記号の後に縦線を引いてその右下に書くという書き方もある。

　記号$\partial$はいろんな読み方がある。この記号はdから来ているので普通に「ディー」と読む場合、それではdと区別がつかないので「丸いd」という意味で「ラウンドディー」と読む場合、それを省略して単に「ラウンド」と読む場合、偏微分（partial differential）から「パーシャル」と読む場合、derivativeの方から「デル」と読む場合がある。微分${\diff y\over \diff x}$を「でぃーわいでぃーえっくす」と読んだのと同様に、$\PD{f}{{\xcol{x}}}$は「でるえふでるえっくす」（あるいは「らうんどえふらうんどえっくす」）のように上から順に読む。

　ここで、$\PD{}{\xcol{x}}$も微分演算子であるので、$\ddx$同様の微分演算子の色を使って書いた。分母にある$\xcol{x}$を色付きにしたのは、偏微分の演算子は$\PD{}{\xcol{x}},\PD{}{\ycol{y}}$といろんな変数に関する微分が同時に出てくるのが普通で、色による区別をつけた方が便利だからである（常微分$\ddx$であれば、変数は$\xcol{x}$だけだろうから色で区別する必要はなかった）。

　偏微分の計算は常微分と同様に行うことができる。たとえば常微分のとき、

　$\ycol{y}=\xcol{x}^2$に含まれる変数$\xcol{x},\ycol{y}$を微小変化させた式は$\ycol{y}+\coldy=(\xcol{x}+\coldx)^2=\xcol{x}^2+2\xcol{x}\coldx+\coldx^2$であり、この式の$\coldx,\coldy$の1次の項の係数を比較すると$\coldy=2\xcol{x}\coldx$となり導関数は${\coldy\over \coldx}=2\xcol{x}$となる。

という計算ができた。偏微分でも同様に、$f\kakko{\xcol{x},\ycol{y}}= \xcol{x}^2\ycol{y}$の微係数（偏微係数）を求めるにはこの関数を微小変化させた結果を \begin{equation} \gunderbrace{\left(\xcol{x}+\coldx\right)^2\left(\ycol{y}+\coldy\right)}_{f\kakko{\xcol{x}+\coldx,\ycol{y}+\coldy}}=\gunderbrace{\xcol{x}^2\ycol{y}}_{f\kakko{\xcol{x},\ycol{y}}}+\gunderbrace{2\xcol{x}\ycol{y}\coldx +\xcol{x}^2\coldy}_{微小変化}+(2次以上の微小量) \end{equation} のように計算する。微小変化の部分が$\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}\coldx +\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}\coldy$と表されるのだから、$\coldx$と$\coldy$の前の係数を比較して、 \begin{equation} \begin{array}{lcll} &\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{{\xcol{x}}}{\ycol{y}}= 2\xcol{x}\ycol{y},&\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}= \xcol{x}^2 \end{array} \end{equation} がわかる。同様に$f\kakko{\xcol{x},\ycol{y}}= \sin (\xcol{x}+\ycol{y}^2)$の場合を考えると \begin{equation} \begin{array}{lcll} &\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}= \cos\kakko{\xcol{x}+\ycol{y}^2},&\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}=2\ycol{y}\cos\kakko{\xcol{x}+\ycol{y}^2}\\ \end{array} \end{equation} である。円柱の体積では、$\pi\rcol{r}^2\xcol{h}\to\pi(\rcol{r}+\coldr)^2(\xcol{h}+\xcol{\mathrm dh})$という微小変化を考えて \begin{equation} \thetacol{\mathrm dV}\kakko{\rcol{r},\xcol{h}} = \goverbrace{\pi \rcol{r}^2}^{\PDC{V}{\xcol{h}}{\rcol{r}}}\xcol{\mathrm dh} + \goverbrace{2\pi\rcol{r}\xcol{h}}^{\PDC{V}{\rcol{r}}{\xcol{h}}}\coldr \end{equation} となる。偏微分係数である$\PDC{V}{\xcol{h}}{\rcol{r}},\PDC{V}{\rcol{r}}{\xcol{h}}$は底面積と側面積という意味のある量になるこのようにある物理量の偏微分係数がまた別の物理量になることはよくある。一つの物理量を偏微分することでいろんな物理量がわかるようになっている。。

　新しい記号を使ってはいるが、この計算は別に目新しいものではなく、テクニックとして難しい点は無い（偏微分ならではの注意点は現段階ではまだ出てきていない。