偏微分の計算

　前回で偏微分の定義まで行ったので、いろいろな計算をしていこう。偏微分の計算は常微分と同様に行うことができる。たとえば常微分のとき、

　$\ycol{y}=\xcol{x}^2$に含まれる変数$\xcol{x},\ycol{y}$を微小変化させた式は$\ycol{y}+\coldy=(\xcol{x}+\coldx)^2=\xcol{x}^2+2\xcol{x}\coldx+\coldx^2$であり、この式の$\coldx,\coldy$の1次の項の係数を比較すると$\coldy=2\xcol{x}\coldx$となり導関数は${\coldy\over \coldx}=2\xcol{x}$となる。

という計算ができた。偏微分でも同様に、$f\kakko{\xcol{x},\ycol{y}}= \xcol{x}^2\ycol{y}$の微係数（偏微係数）を求めるにはこの関数を微小変化させた結果を \begin{equation} \gunderbrace{\left(\xcol{x}+\coldx\right)^2\left(\ycol{y}+\coldy\right)}_{f\kakko{\xcol{x}+\coldx,\ycol{y}+\coldy}}=\gunderbrace{\xcol{x}^2\ycol{y}}_{f\kakko{\xcol{x},\ycol{y}}}+\gunderbrace{2\xcol{x}\ycol{y}\coldx +\xcol{x}^2\coldy}_{微小変化}+(2次以上の微小量) \end{equation} のように計算する。微小変化の部分が$\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}\coldx +\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}\coldy$と表されるのだから、$\coldx$と$\coldy$の前の係数を比較して、 \begin{equation} \begin{array}{lcll} &\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{{\xcol{x}}}{\ycol{y}}= 2\xcol{x}\ycol{y},&\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}= \xcol{x}^2 \end{array} \end{equation} がわかる。同様に$f\kakko{\xcol{x},\ycol{y}}= \sin (\xcol{x}+\ycol{y}^2)$の場合を考えると \begin{equation} \begin{array}{lcll} &\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}= \cos\kakko{\xcol{x}+\ycol{y}^2},&\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}=2\ycol{y}\cos\kakko{\xcol{x}+\ycol{y}^2}\\ \end{array} \end{equation} である。

　新しい記号を使ってはいるが、この計算は別に目新しいものではなく、テクニックとして難しい点は無い（偏微分ならではの注意点は現段階ではまだ出てきていない。

　常微分の導関数または微係数は極限を使うと$\ddx f\kakko{\xcol{x}}=\lim_{\xcol{\Delta x}\to0}{f\kakko{\xcol{x}+\xcol{\Delta x}}-f\kakko{\xcol{x}}\over \xcol{\Delta x}}$と表すことができた。これと同様に、

偏導関数の定義

\begin{equation} \PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}= \lim_{\xcol{\Delta x}\to0}{ f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}}-f\kakko{\xcol{x},\ycol{y}} \over \xcol{\Delta x} }\label{hendoukansuuteigi} \end{equation} と表せる。もう一つの変数$\ycol{y}$がついている（しかし定数として扱っている）以外は常微分と同じ計算である。もちろん、立場を入れ替えた$\xcol{x}$を一定として$\ycol{y}$で偏微分は \begin{equation} \PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} =\lim_{\ycol{\Delta y}\to0}{ f\kakko{\xcol{x},\ycol{y}+\ycol{\Delta y}}-f\kakko{\xcol{x},\ycol{y}} \over \ycol{\Delta y} }\label{delfdely} \end{equation} である。どちらも、一方で微分するときはもう一方をあたかも定数であるかのように扱っている。ここまでの話として、常微分が偏微分に変わったことで特に難しいところはないはずだ。

　ここで標語を書いておこう。

偏微分には方向がある

　偏微分では「どの方向の変化に対する変化量なのか（どのように独立変数を変化させたときの従属変数の変化量なのか）」が常に大事である。

　考えるべき「偏微分の方向」の代表として、次の図のような二つの方向の微分を考えよう。

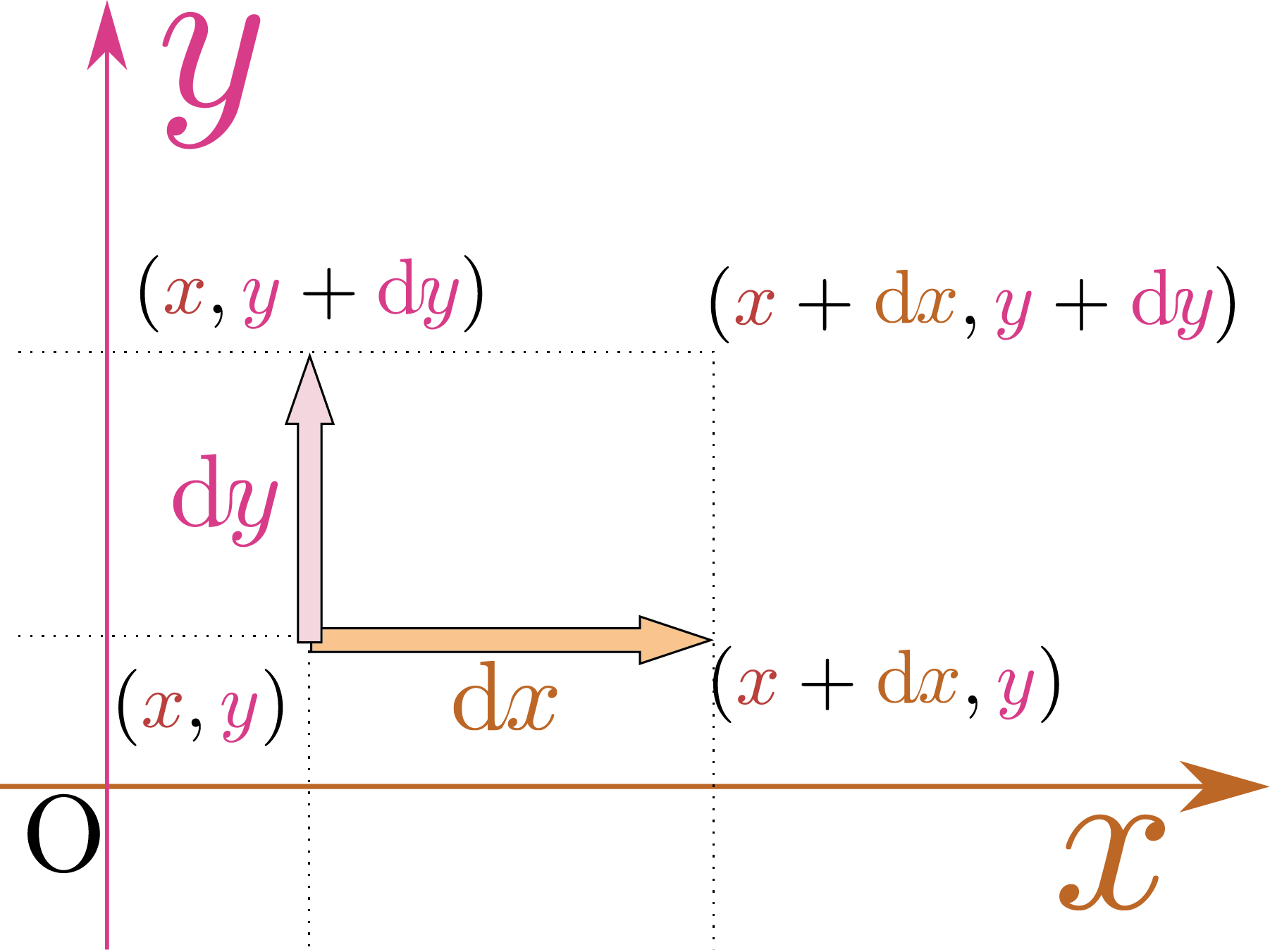
　場所$(\xcol{x},\ycol{y})$を「基準点」として、その場所での関数$f$の値（$f\kakko{\xcol{x},\ycol{y}}$）との比較を行う。

　$\xcol{x}$方向の偏微分」は場所$(\xcol{x}+\coldx,\ycol{y})$での、$\ycol{y}$方向の偏微分」は場所$(\xcol{x},\ycol{y}+\coldy)$での$f$の値との差を考えるものである。

　$f\kakko{\xcol{x},\ycol{y}}$をグラフのもう一つの軸として立体グラフを描くと、下の図のように偏微分係数$\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}$と$\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}$が定義される。

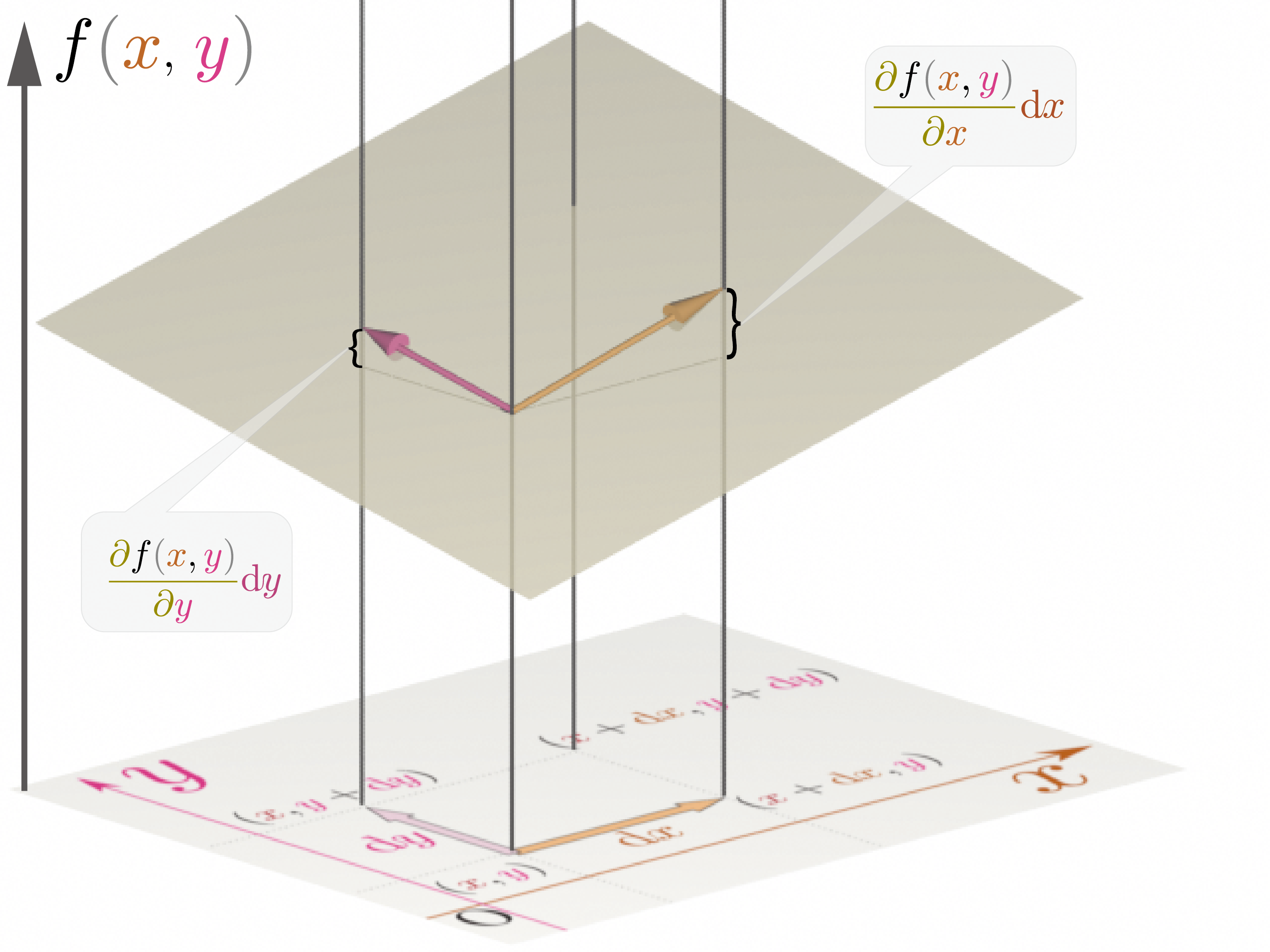
の矢印の先と根元での$f$の値の差は$\coldx$に比例するので、その比例係数が$\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}$。

の矢印の先と根元での$f$の値の差は$\coldy$に比例するので、その比例係数が$\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}$。

常微分では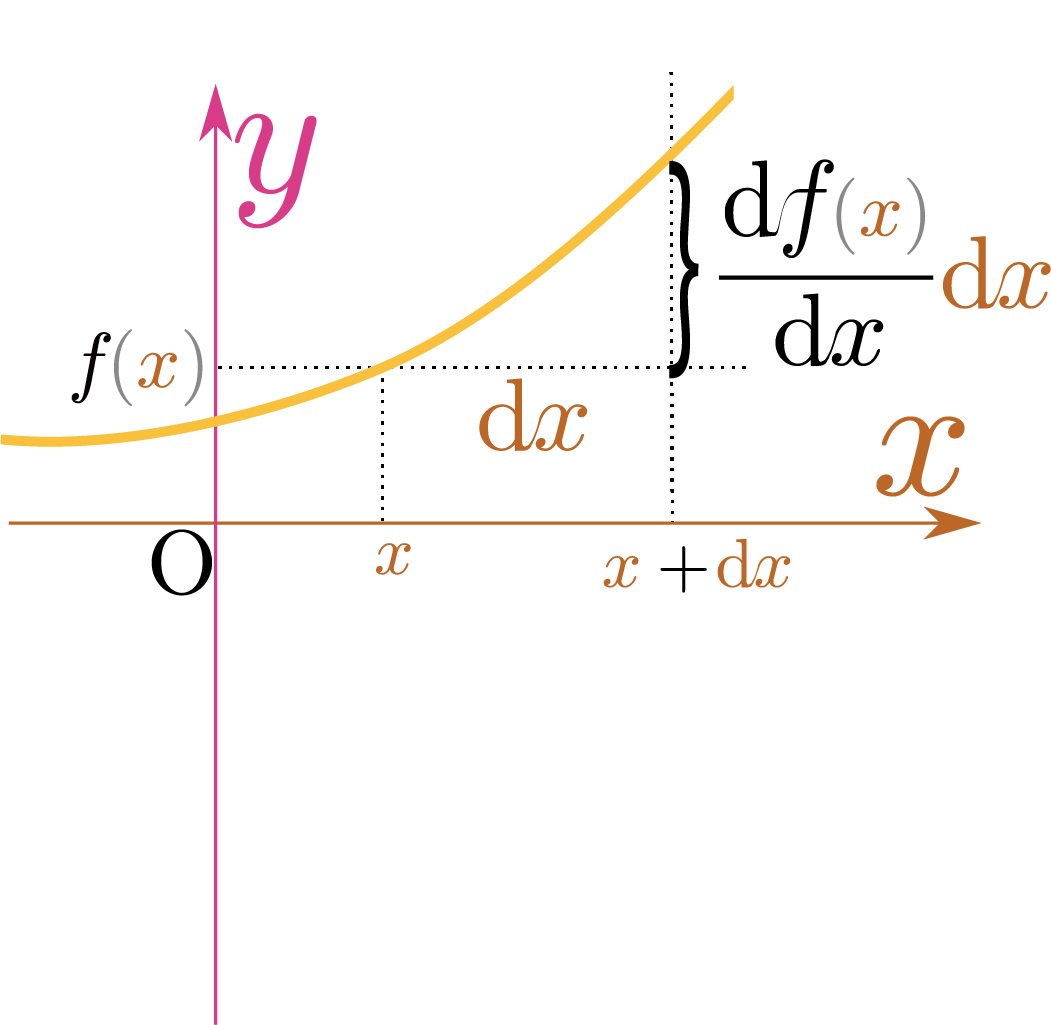のように微係数のイメージを捉えることができたが、偏微分ではこれが2方向のそれぞれで定義されている。

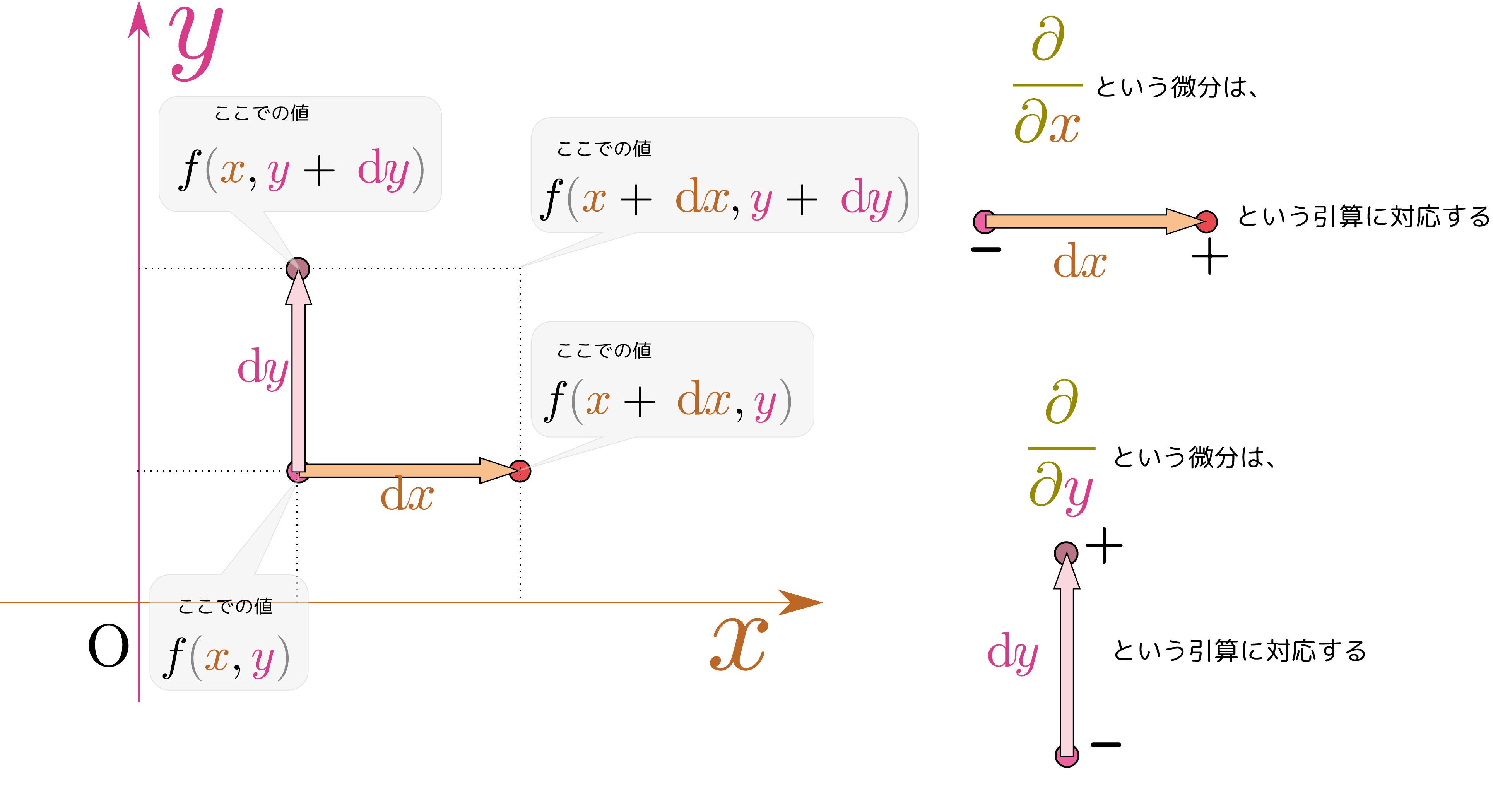
　上の図に、二つの微分の意味を図解した。矢印の先（$+$と書いたところ）から矢印の根元（$-$と書いたところ）を引く、というのが（たとえば$f\kakko{\xcol{x}+\coldx,\ycol{y}}-f\kakko{\xcol{x},\ycol{y}}$）が偏微分という計算の本質になるこの後$\xcol{\Delta x}$で割って$\xcol{\Delta x}\to0$の極限を取って、という手続きが続くが、本質は「矢印の先と元の引算」なのである。}。場所$(\xcol{x}+\coldx,\ycol{y})$と場所$(\xcol{x},\ycol{y})$での$f$の値の引算は \begin{equation} f\kakko{\xcol{x}+\coldx,\ycol{y}}-f\kakko{\xcol{x},\ycol{y}}=\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}\coldx \end{equation} となる。同様に場所$(\xcol{x},\ycol{y}+\coldy)$と場所$(\xcol{x},\ycol{y})$の$f$の値の引算は \begin{equation} f\kakko{\xcol{x},\ycol{y}+\coldy}-f\kakko{\xcol{x},\ycol{y}} =\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}\coldy \end{equation} になる。

高階の偏微分

　偏微分も常微分同様、二階微分がある。その記号も \begin{equation} \PDIC{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}}{\xcol{x}}{\ycol{y}} =\PPDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} ,~~ \PDIC{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}}{\ycol{y}}{\xcol{x}} =\PPDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \end{equation} のように常微分の場合に似た書き方にする（三階以上も同様である）。これら二つの偏微分が（それぞれ$\xcol{x}$方向と$\ycol{y}$方向の）曲がり具合を表現しているのは、1変数の場合と同様である。

　偏微分の二階微分には、 \begin{equation} \PDIC{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}}{\xcol{x}}{\ycol{y}}=\PPDD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} \end{equation} のように「最初に$\ycol{y}$で微分、次に$\xcol{x}$で微分」もある（上の式の右辺は固定する変数を省略する書き方を使った。$\PPDD{f}{\xcol{x}}{\ycol{y}}$は$\PD{}{\xcol{x}}\left(\PD{f}{\ycol{y}}\right)$の省略形である。分母の書き方が常微分と決定的に違うところなので注意しようここで、$\PPDD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$と$\PPDD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}$は違うのか？---という疑問を持った人もいるだろう。微分可能な関数に対してはこの二つは等しい。それは、上の式が$\xcol{x}\leftrightarrow\ycol{y}$の取り換えに対して対称であることからもある程度納得できる。。

　定義にしたがって計算すれば、この二階微分は \begin{equation} \begin{array}{rl} & \lim_{\xcol{\Delta x}\to0\atop\ycol{\Delta y}\to0} {\left( f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}+\ycol{\Delta y}} -f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}}\right) -\left(f\kakko{\xcol{x},\ycol{y}+\ycol{\Delta y}} -f\kakko{\xcol{x},\ycol{y}} \right) \over \xcol{\Delta x}\ycol{\Delta y}} \\ = & \lim_{\xcol{\Delta x}\to0\atop\ycol{\Delta y}\to0} { f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}+\ycol{\Delta y}} -f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}} -f\kakko{\xcol{x},\ycol{y}+\ycol{\Delta y}} +f\kakko{\xcol{x},\ycol{y}} \over \xcol{\Delta x}\ycol{\Delta y}} \end{array}\label{delxdely} \end{equation} という量を計算している。図で描くと、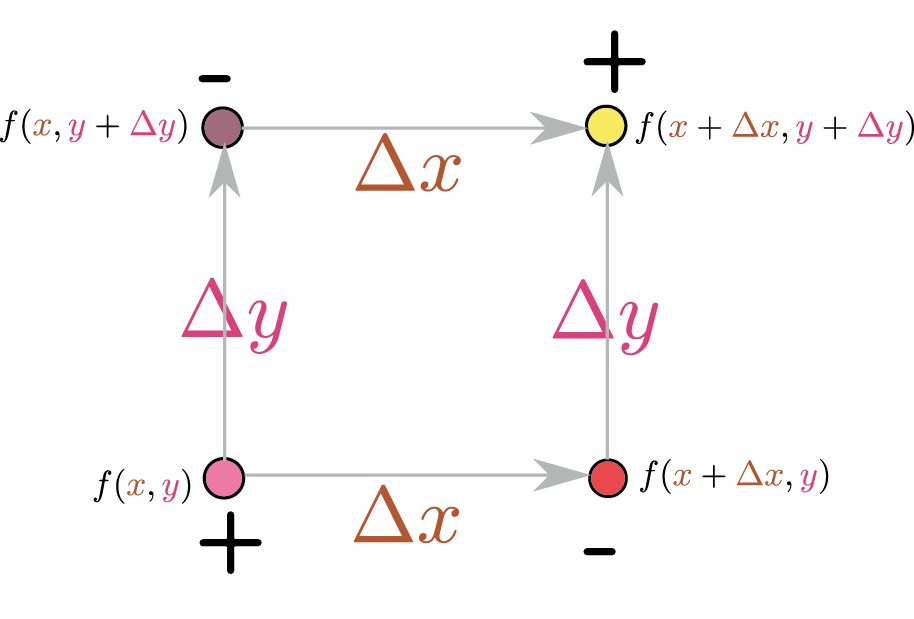のような計算を行っている。

　この二階微分も曲がり具合を表現している。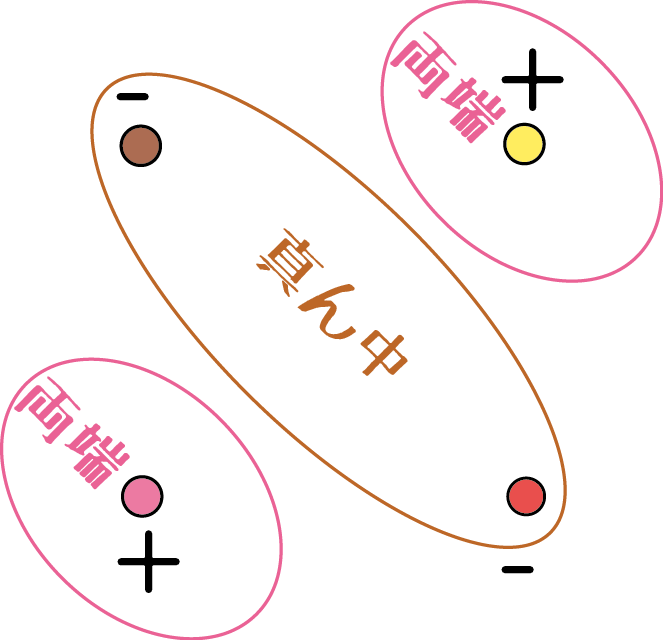のように考えると、斜め方向に見て「真ん中」と「両端」で引算をしている。

2変数関数のテイラー展開

　1変数のテイラー展開と同様に考えるもちろん、どんな関数でもテイラー展開できるわけではない。ここではできるものだけを扱う。と、 \begin{equation} \begin{array}{rl} f\kakko{\xcol{x},\ycol{y}} =&f\kakko{x_0,y_0} +\PD{f\kakko{x_0,y_0}}{\xcol{x}}(\xcol{x}-x_0) +\PD{f\kakko{x_0,y_0}}{\ycol{y}}(\ycol{y}-y_0)\\ +&{1\over 2}\PPD{f\kakko{x_0,y_0}}{\xcol{x}}(\xcol{x}-x_0)^2 +\PPDD{f\kakko{x_0,y_0}}{\xcol{x}}{\ycol{y}}(\xcol{x}-x_0)(\ycol{y}-y_0) +{1\over 2}\PPD{f\kakko{x_0,y_0}}{\ycol{y}}(\ycol{y}-y_0)^2 \\ +&{1\over 3!}\opcol{\partial^3 \kuro{f\kakko{x_0,y_0}}\over \partial {\xcol{x}}^3}(\xcol{x}-x_0)^3 +{1\over 2}\opcol{\partial^3 \kuro{f\kakko{x_0,y_0}}\over \partial {\xcol{x}}^2\partial {\ycol{y}}}(\xcol{x}-x_0)^2(\ycol{y}-y_0) +{1\over 2}\opcol{\partial^3 \kuro{f\kakko{x_0,y_0}}\over \partial {\xcol{x}}\partial {\ycol{y}}^2}(\xcol{x}-x_0)(\ycol{y}-y_0)^2\\ +&{1\over 3!}\opcol{\partial^3 \kuro{f\kakko{x_0,y_0}}\over \partial {\ycol{y}}^3}(\ycol{y}-y_0)^3+\ldots \end{array} \end{equation} のようになる$\PD{f\kakko{x_0,y_0}}{\xcol{x}}$などと書いているのは、全て微分が終了した後で$\xcol{x}=x_0,\ycol{y}=y_0$を代入するという意味である。。一般項を表現すると次のようになる。 \begin{equation} f\kakko{\xcol{x},\ycol{y}} = \sum_{m=0}^\infty\sum_{n=0}^\infty {1\over m! n!}\opcol{\partial^{m+n} \kuro{f\kakko{\xcol{x},\ycol{y}}}\over \partial {\xcol{x}}^m \partial {\ycol{y}}^n}\biggr|_{\xcol{x}=x_0\atop \ycol{y}=y_0} (\xcol{x}-x_0)^m(\ycol{y}-y_0)^n \label{ippannitaylor} \end{equation}

　なお、$\opcol{\partial^{m+n} \kuro{f\kakko{\xcol{x},\ycol{y}}}\over \partial {\xcol{x}}^m \partial {\ycol{y}}^n}$は$f\kakko{\xcol{x},\ycol{y}}$を$\xcol{x}$で$m$回、$\ycol{y}$で$n$回、偏微分を行ったものである。

　1変数のときと同様に、和を途中で打ち切る場合には剰余項が出る。また、テイラー展開には有効な範囲（収束半径）があることも1変数の場合と同様である。

2変数関数の極大極小

　1変数関数の極大・極小点では導関数が0になったが、多変数（ここでは「2変数」のみを扱う）関数の場合も極大・極小点で導関数が0になるのは同じである。ただし、多変数なら「微分の方向」があるので「ある方向では0だが、別の方向では0でない」ことが起こりえる。

　次の図に示したのは$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}^2+\ycol{y}^2,-\xcol{x}^2-\ycol{y}^2,\xcol{x}^2-\ycol{y}^2$の三つの関数の3次元グラフで、どの場合も原点においてどの方向の微分も0であるが、二階微分の値の正負が違う。

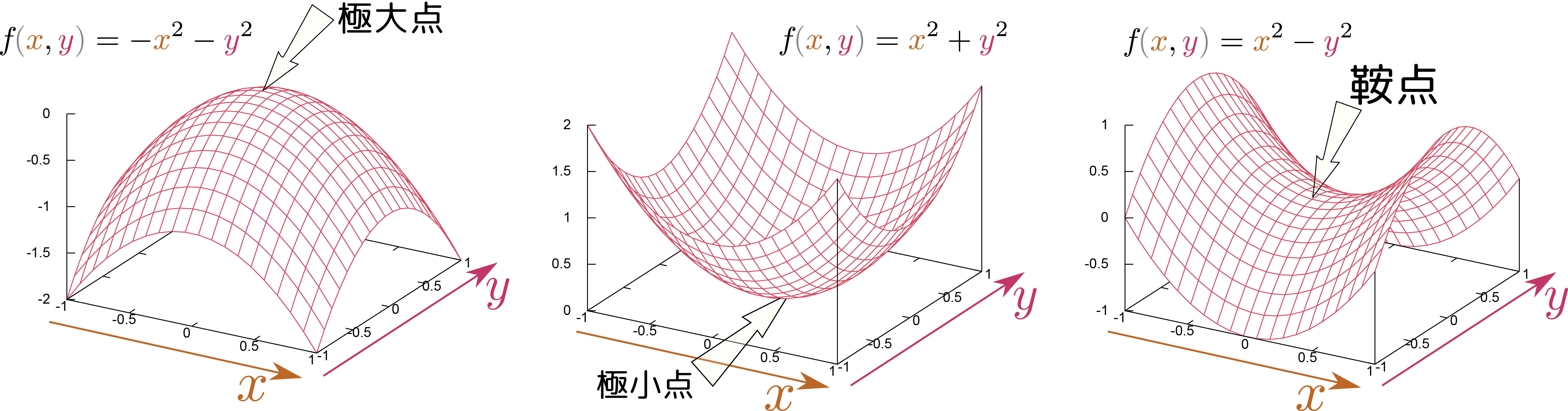
　どの方向に対しても一階微分が0で二階微分が負なら、それは極大点である。逆に、どの方向に対しても一階微分が0で二階微分が正なら、それは極小点である（ここまでは1変数のときの素直な拡張である）。多変数で現れる新しい状況として「一階微分はどの方向に対しても0であるが、二階微分の正負は方向により異なる」という場合があり、この場合は（図に示したように馬の鞍の形なので）「鞍点(saddle point)」と呼ぶ 上の図では示してないが、ある方向の二階微分が0であるという状況ももちろんある。というより、鞍点の場合「二階微分が正である方向」と「負である方向」があるのだから、方向を少しずつ変えていけば、二階微分が0になる方向が必ず見つかる。。

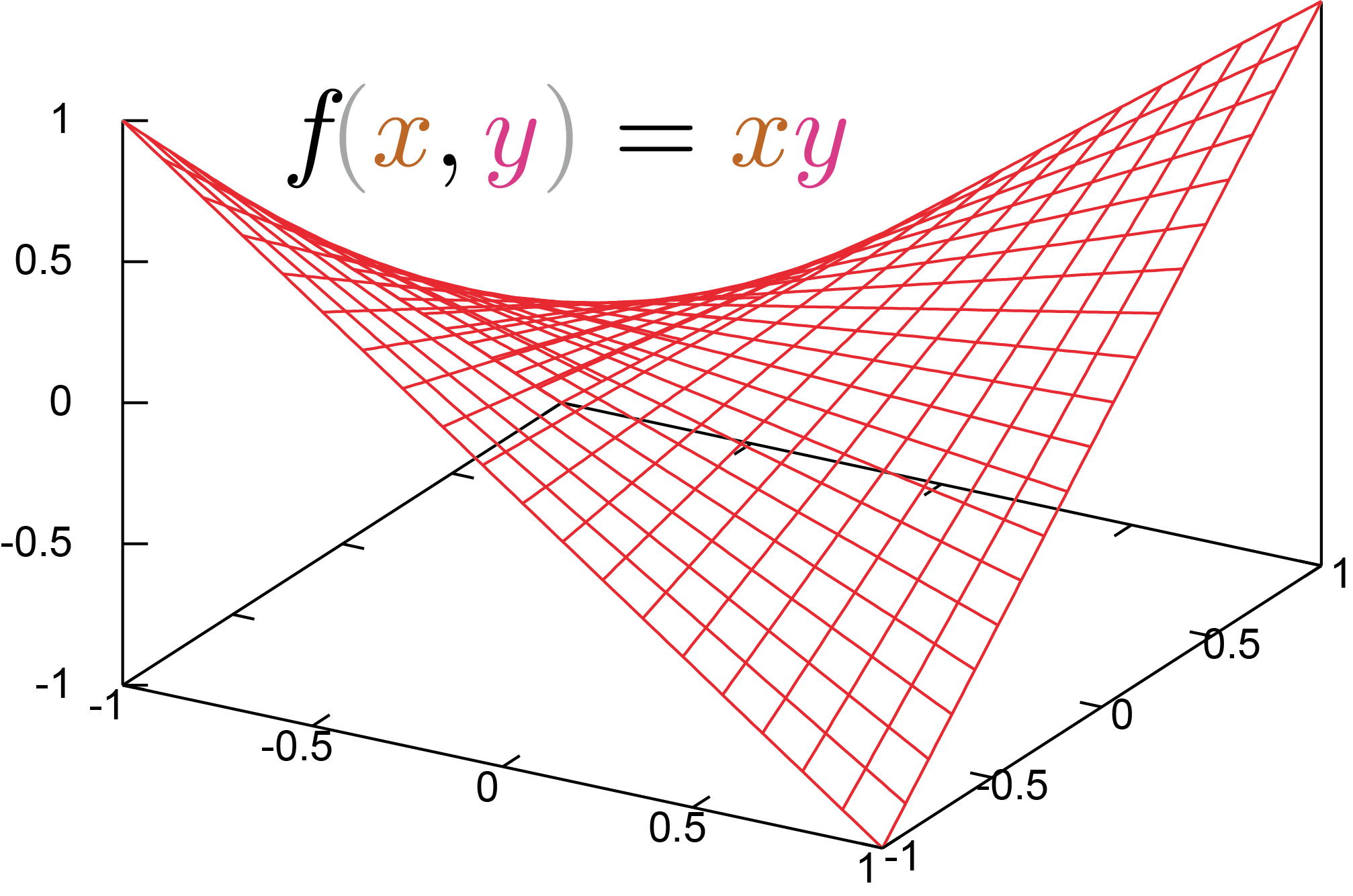
　上では比較的単純な例を提示したので、$\PPD{f}{\xcol{x}}$と$\PPD{f}{\ycol{y}}$の正負を見て場合分けできたが、2変数関数の二階微分はもう一つ、$\PPDD{f}{\xcol{x}}{\ycol{y}}$もある（上の例では全て$\opcol{\partial^2 \kuro{f}\over \partial \xcol{x}\partial \ycol{y}}=0$なので気にしなくてもよかった）。

　$\PPDD{f}{\xcol{x}}{\ycol{y}}\neq0$の例として、右のグラフこのグラフは$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}^2-\ycol{y}^2$を${\pi\over 4}$だけ回転して、少し高さを調整したものになっている。の関数$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}\ycol{y}$は原点$(0,0)$で$\PPDD{f}{\xcol{x}}{\ycol{y}}=1$であり、鞍点になっている。

　一般の2変数関数で、一階微分が全て0である点（このような点は「停留点(stationary point)」と呼ぶ）が見つかったとして、その点が極大なのか極小なのかそれとも鞍点なのかを知りたい場合は、テイラー展開の2次の項を詳しく調べる必要がある。$(x_0,y_0)$が停留点とすればそこで一階微分は0だから、$(\xcol{x}-x_0)=\xcol{\Delta x},(\ycol{y}-y_0)=\ycol{\Delta y}$と書けば、 \begin{equation} f\kakko{\xcol{x},\ycol{y}} =f\kakko{x_0,y_0} +\goverbrace{\gunderbrace{{1\over 2}\PPD{f}{\xcol{x}}}_a(\xcol{\Delta x})^2 +\gunderbrace{\PPDD{f}{\xcol{x}}{\ycol{y}}}_b\xcol{\Delta x}\ycol{\Delta y} +\gunderbrace{{1\over 2}\PPD{f}{\ycol{y}}}_c(\ycol{\Delta y})^2}^{曲がり具合を表現する部分} +\ldots \end{equation} となる。3次以上の項$(\ldots)$は省略した。式に示したように、係数を以下$a,b,c$で表す。

　上の「曲がり具合を表現する部分」がどのような$\xcol{\Delta x},\ycol{\Delta y}$に対しても正であるならばこの点は極小点、逆に常に負ならば極大点である。正にも負にもなる場合は鞍点だと言える（他の可能性としては正、負ではなく0以上や0以下という可能性もある）。この式は \begin{equation} a(\xcol{\Delta x})^2 + b\xcol{\Delta x}\ycol{\Delta y}+c(\ycol{\Delta y})^2 =\gunderbrace{(\ycol{\Delta y})^2}_{常に正}\gunderbrace{ \left( a\left({\xcol{\Delta x}\over\ycol{\Delta y} }\right)^2 +b{\xcol{\Delta x}\over\ycol{\Delta y} }+c \right)}_{この部分の正負が問題} \end{equation} となるから、$\tcol{t}={\xcol{\Delta x}\over\ycol{\Delta y} }$とすれば後は「\文中式{二次式$a\tcol{t}^2+b\tcol{t}+c$}の正負」が問題$\tcol{t}={\xcol{\Delta x}\over\ycol{\Delta y} }$の変域は実数全体。$\xcol{\Delta x}=\sqrt{(\xcol{\Delta x})^2+(\ycol{\Delta y})^2}\cos\alpha,\ycol{\Delta y}=\sqrt{(\xcol{\Delta x})^2+(\ycol{\Delta y})^2}\sin\alpha$と置けば、${\xcol{\Delta x}\over\ycol{\Delta y} }=\cot \alpha$。になり、

• $b^2-4ac>0$ の場合:　　正にも負にもなる（鞍点）
• $b^2-4ac<0$~かつ~$a>0$の場合:　常に正（極小点）
• $b^2-4ac<0$~かつ~$a<0$の場合:　常に負（極大点）

　この判別式$b^2-4ac$というのは実は$\left(\begin{array}{cc}\opcol{\partial^2 \kuro{f}\over \partial \xcol{x}^2}&\opcol{\partial^2 \kuro{f}\over \partial \xcol{x}\partial {\ycol{y}}}\\[3mm]\opcol{\partial^2 \kuro{f}\over \partial {\ycol{y}}\partial \xcol{x}}&\opcol{\partial^2 \kuro{f}\over \partial {\ycol{y}}^2}\end{array}\right)$という行列（「ヘッセ行列(Hessian matrix)」と呼ぶ）の行列式の$-1$倍である。この行列の固有値の正負で極大極小が判定できる。行列の形で書くと、3変数以上の場合にも拡張できる。

偏微分の交換可能性

　偏微分の順番に関する疑問について前に述べた。ここで、 \begin{equation} \opcol{\left( {\partial\over \partial \xcol{x}}\kuro{\left(\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\right)}\right)_{\!\!\ycol{y}}} =\opcol{\left( {\partial\over \partial \ycol{y}}\kuro{\left(\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\right)}\right)_{\!\!\xcol{x}}} \label{henbibunkoukan} \end{equation} であること、すなわち「$\xcol{x}$で偏微分してから$\ycol{y}$で偏微分」と、この順番を変えたものが同じ結果になることを確認しておこう（これを「偏微分が交換する」と表現する）。上で計算したように、 \begin{equation} \opcol{\left( {\partial\over \partial \xcol{x}}\kuro{\left(\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\right)}\right)_{\!\!\ycol{y}}} =\lim_{\xcol{\Delta x}\to0\atop\ycol{\Delta y}\to0} { f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}+\ycol{\Delta y}} -f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}} -f\kakko{\xcol{x},\ycol{y}+\ycol{\Delta y}} +f\kakko{\xcol{x},\ycol{y}} \over \xcol{\Delta x}\ycol{\Delta y}}\label{DyDxf} \end{equation} である。$\xcol{x}$と$\ycol{y}$の微分の順番を変えると、 \begin{equation} \begin{array}{rl} \opcol{\left( {\partial\over \partial \ycol{y}}\kuro{\left(\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\right)}\right)_{\!\!\xcol{x}}} =& \lim_{\xcol{\Delta x}\to0\atop\ycol{\Delta y}\to0} { f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}+\ycol{\Delta y}} -f\kakko{\xcol{x},\ycol{y}+\ycol{\Delta y}} -f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}} +f\kakko{\xcol{x},\ycol{y}} \over \xcol{\Delta x}\ycol{\Delta y}} \end{array}\label{DxDyf} \end{equation} を得る。

　図で表現しておこう。省略形が$\PD{}{\ycol{y}}\left(\PD{f}{\xcol{x}}\right)$になる微分を図で表現したのが次の図である。

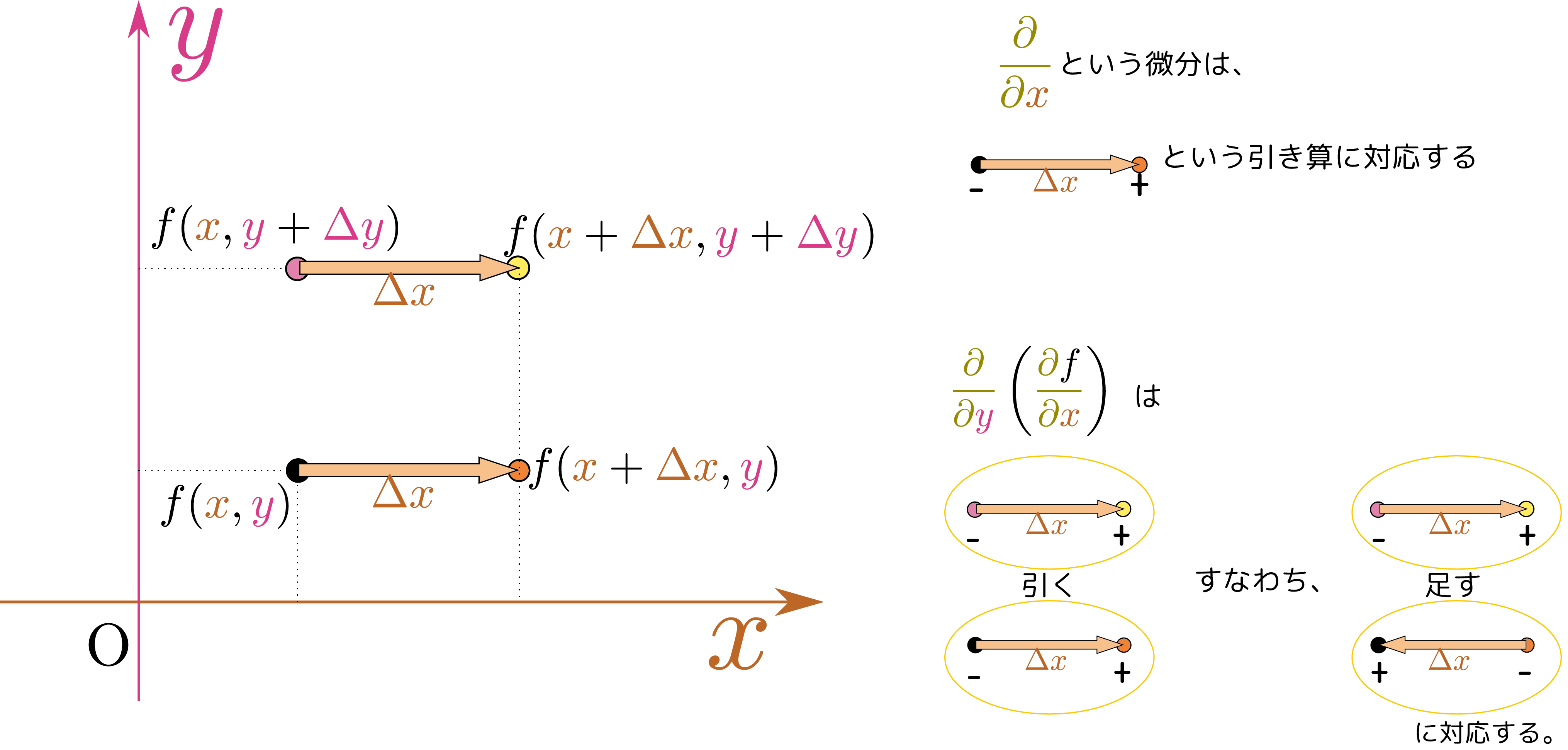
　一方、$\xcol{x}$と$\ycol{y}$の立場を取り替えた$\opcol{\partial \over \partial \xcol{x}}\left(\opcol{\partial \kuro{f}\over \partial \ycol{y}}\right)$は次の図のように書ける。

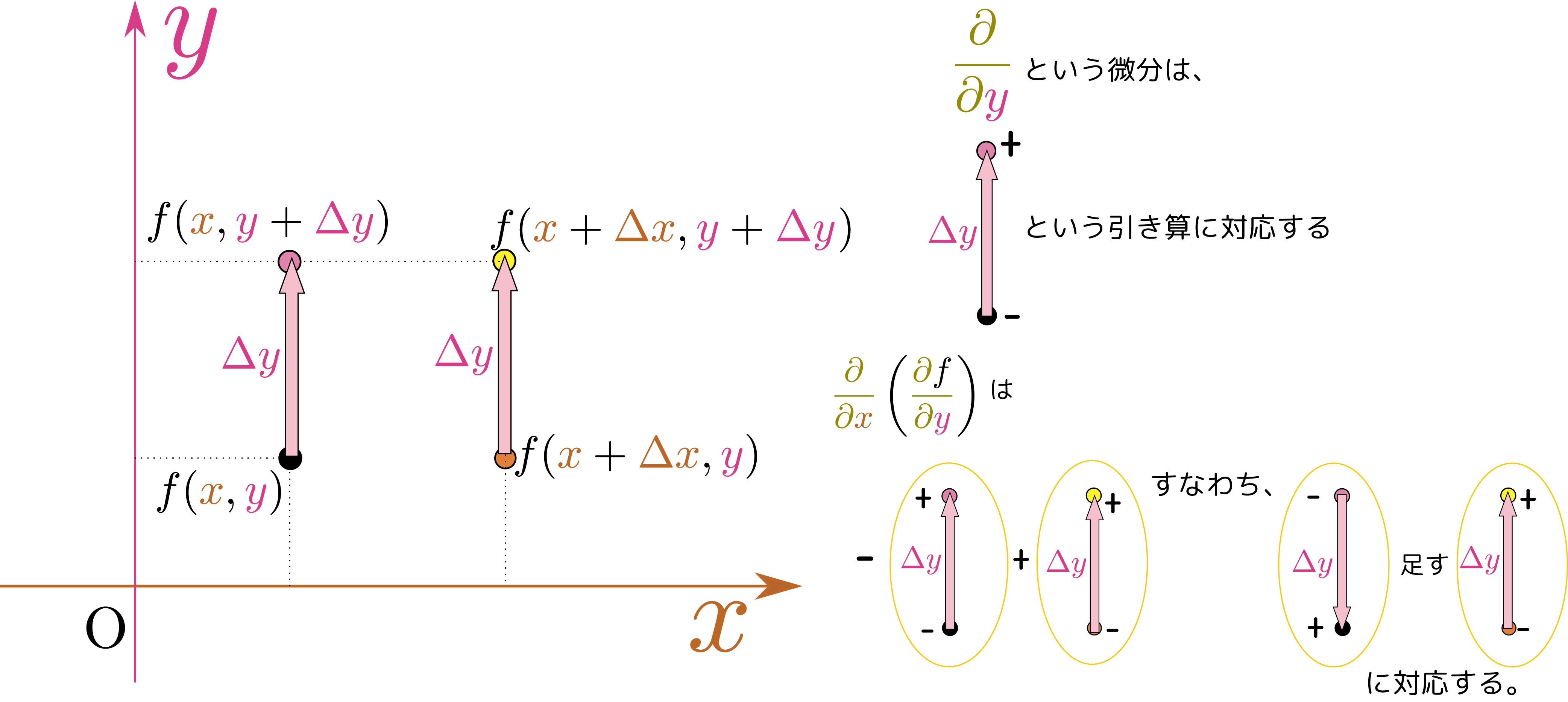
　最終結果は、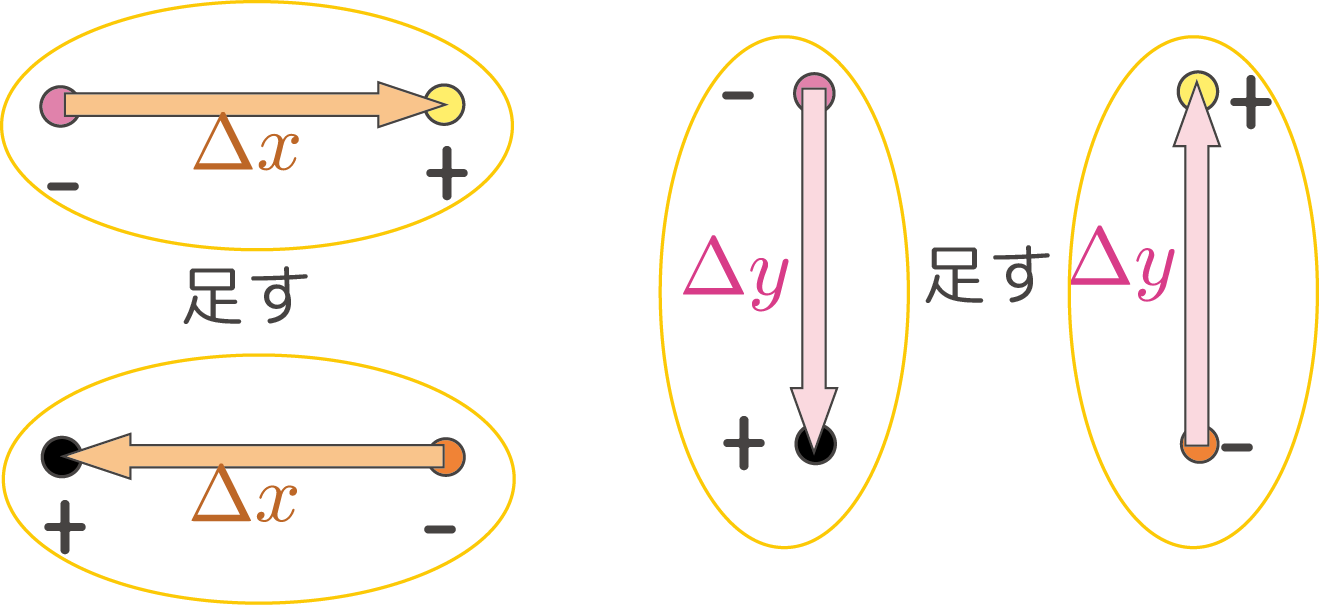と、同じ量になっているので、二つの微分は同じになる。別の言い方をすると、操作$\left(\PD{}{\xcol{x}}\fbox{？}\right)_{\!\!\ycol{y}}$と操作$\left(\PD{}{\ycol{y}}\fbox{？}\right)_{\!\!\xcol{x}}$は交換する。この$\fbox{？}$には何が入ってもよい。三階以上の微分に対しても同じことが言える。

　ただし、これが成立するためには関数が微分可能でなくてはいけないことはもちろんである。微分可能でない場合は上で計算した極限が一致しないことがある。

　たとえば、$f\kakko{\xcol{x},\ycol{y}}= {\xcol{x}^3\ycol{y}\over \xcol{x}^2+\ycol{y}^2}$}の原点における偏微分は交換しない。こうなる理由は原点では分母が0になってこの関数が定義されていないからである。