偏微分の注意点

$\def\coldr{\rcol{\mathrm dr}}\def\coldvecx{\xcol{\mathrm d\vec x}}\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{~~~~~~~{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}\def\kidy{\opcol{\diff y}}\def\ve{\vec{\mathbf e}}\def\colvecx{\xcol{\vec x}}\definecolor{usuopcolor}{RGB}{237,234,203}\def\usuopcol#1{\color{usuopcolor}#1}\def\vgrad#1{{\usuopcol{\overrightarrow{\opcol{\rm grad}~\kuro{#1}}}}}\def\dX{\rcol{\mathrm dX}}\def\dY{\thetacol{\mathrm dY}}\def\opdf{\opcol{\mathrm df}}\def\coldf{\tcol{\mathrm df}}\def\dtwof{\opcol{\mathrm d^2f}}\def\murasakidb{\zcol{\mathrm d b}}\def\ao{\ycol}\def\aodV{\ycol{\diff V}}\def\aka{\xcol}\def\akadm{\xcol{\diff m}}\def\gunderbrace{\underbrace}$

偏微分の注意点

　偏微分の計算を行うときに有用な公式と、誤りやすい注意点を述べておく。特に常微分の場合とは違う点をまとめておこう。

${\partial a\over \partial b}\neq{1\over {\partial b\over \partial a}}$

よくある誤り

　極座標と直交座標の変換${\xcol{x}=\rcol{r}\cos\thetacol{\theta}\atop\ycol{y}=\rcol{r}\sin \thetacol{\theta}}$で、$\xcol{x}=\rcol{r}\cos \thetacol{\theta}$を$\rcol{r}$で偏微分すると$\PD{x}{\rcol{r}}=\cos\thetacol{\theta}$と計算できる。ゆえに$\PD{r}{\xcol{x}}={1\over \cos\thetacol{\theta}}$だろう。

　これに限らず、常微分であれば成立する${\coldy\over \coldx}={1\over {\coldx\over \coldy}}$との類推で、偏微分でも「分母」と「分子」を入れ替える$\left({\partial a\over \partial b}\to {\partial b\over \partial a}\right)$と逆数になる$\left({\partial a\over \partial b}={1\over {\partial b\over \partial a}}\right)$と勘違いしてしまいがちである。

　実際に$\rcol{r}$を$\xcol{x}$で微分という計算をするために$\rcol{r}$を$\xcol{x},\ycol{y}$を独立変数として表すと$r\,\kakko{\xcol{x},\ycol{y}}=\sqrt{\xcol{x}^2+\ycol{y}^2}$となる。これから$\PD{r}{\xcol{x}}$を計算すると \begin{equation} \PD{r\,\kakko{\xcol{x},\ycol{y}}}{\xcol{x}} = \PD{\left(\sqrt{\xcol{x}^2+\ycol{y}^2}\right)}{\xcol{x}} = {1\over 2\sqrt{\xcol{x}^2+\ycol{y}^2}}\times 2\xcol{x}={\xcol{x}\over \sqrt{\xcol{x}^2+\ycol{y}^2}}=\cos\thetacol{\theta} \end{equation} となる。一方で上に書いたように \begin{equation} \PD{x\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}} = \PD{\left(\rcol{r}\cos\thetacol{\theta}\right)}{\rcol{r}} =\cos\thetacol{\theta} \end{equation} である。つまりこの場合$\PD{r}{\xcol{x}}=\PD{x}{\rcol{r}}$なのだ。$\PD{x}{\rcol{r}}={1\over \PD{r}{\xcol{x}}}$と誤解してしまうのは、省略記法を使っているからである。省略せずに書くと$\PD{x}{\rcol{r}}$は$\PDC{x\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}{\thetacol{\theta}}$で$\PD{r}{\xcol{x}}$は$\PDC{r\,\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$である。${\opcol{\biggr)}}_{\thetacol{\theta}}$と${\opcol{\biggr)}}_{\ycol{y}}$の違いに注意。「どの変数を固定しているか」は大事なのである。

　ここで教科書とは順番を変えて、以下の問題を手を動かして解いてもらった。

　$\zcol{X}=\xcol{x}+\ycol{y},\thetacol{Y}=\xcol{x}-\ycol{y}$のような簡単な例でも、$\PDC{X\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$と$\PDC{x\,\kakko{\zcol{X},\thetacol{Y}}}{\zcol{X}}{\thetacol{Y}}$は逆数になっていない。確認せよ。

　$\zcol{X}=\xcol{x}+\ycol{y}$を（$\ycol{y}$を一定として）$\xcol{x}$で微分すると、${\partial X\over \partial x}=1$となる（なぜか${\partial X\over \partial x}=1+\ycol{y}$というおかしな答えを出していた人がいたが、$\ycol{y}$を定数とみなして微分するのだから、$\ycol{y}$は消える）。

　一方、$\xcol{x}={\zcol{X}+\thetacol{Y}\over2}$なので、${\partial x\over\partial X}={1\over2}$となって逆数にならない。

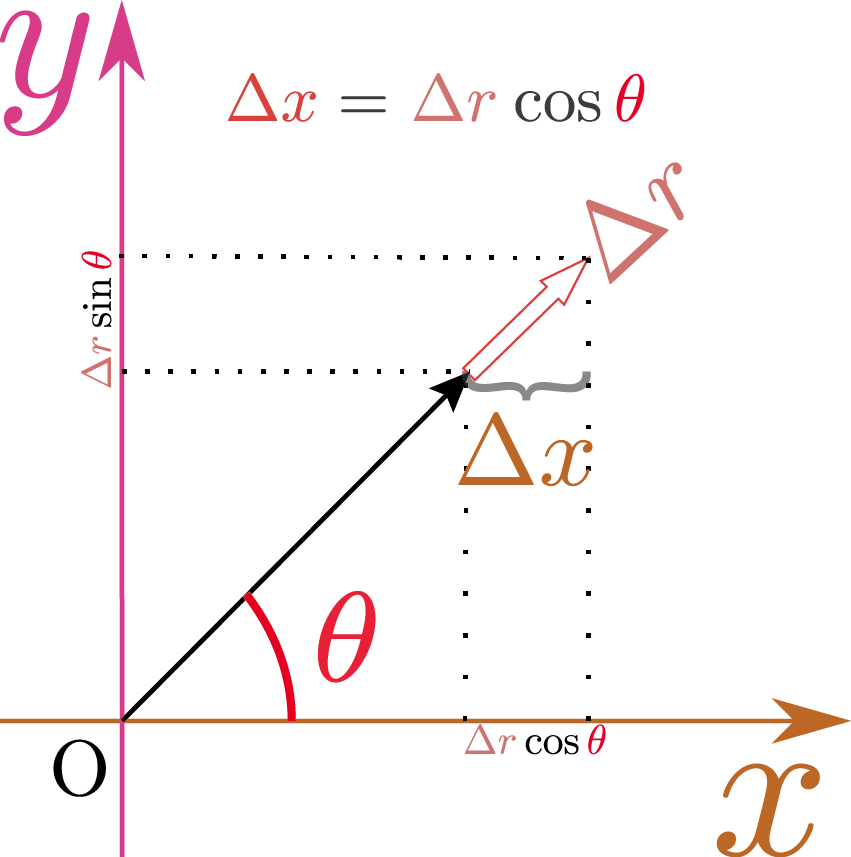
　$\PDC{\rcol{r}}{\xcol{x}}{\ycol{y}}$も$\PDC{\xcol{x}}{\rcol{r}}{\thetacol{\theta}}$も$\cos\thetacol{\theta}$となることを、図解しておこう。右の図は、$\thetacol{\theta}$を一定にして$\rcol{r}$で微分する操作を図解したものである。矢印の方向（これは$\rcol{r}$が増える方向、すなわち原点から離れる方向である）に$\rcol{\Delta r}$移動すると、$\xcol{x}$方向には$\rcol{\Delta r}\cos\thetacol{\theta}$（$\ycol{y}$方向には$\rcol{\Delta r}\sin\thetacol{\theta}$）だけ移動することになる。よって、 \begin{equation} {\xcol{\Delta x}\over \rcol{\Delta r}}=\cos\thetacol{\theta}\label{rdaix} \end{equation} となる。この後$\rcol{\Delta r}\to0$の極限を取ったものが$\PDC{\xcol{x}}{\rcol{r}}{\thetacol{\theta}}$である。　

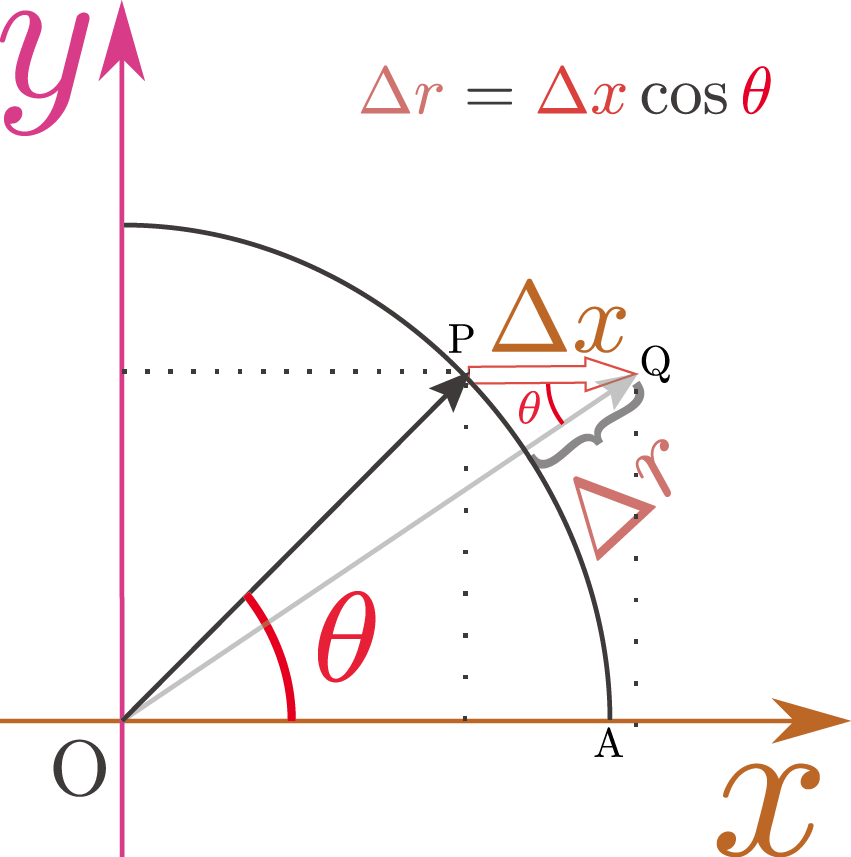
　一方、$\ycol{y}$を一定にして$\xcol{x}$で微分する操作を図解したものが右の図である。図で、$\angle {\rm OQP}$と$\angle{\rm POA}$すなわち$\thetacol{\theta}$が等しいとしている。$\angle {\rm OQP}=\angle{\rm QOA}$なのは錯角であることからわかる。$\xcol{\Delta x}$はいずれ$\to0$の極限を取る微小量なので、$\angle{\rm POA}$と$\angle{\rm QOA}$の差は高次の微小量として無視できるので、$\angle{\rm OQP}=\thetacol{\theta}$となる。$\xcol{\Delta x}$を斜辺とする直角三角形を見ると \begin{equation} {\rcol{\Delta r}\over \xcol{\Delta x}}=\cos\thetacol{\theta}\label{xdair} \end{equation} がわかり、この$\xcol{\Delta x}\to0$の極限の結果が$\PDC{\rcol{r}}{\xcol{x}}{\ycol{y}}=\cos \thetacol{\theta}$である。

　逆に「どの変数を固定しているのか」が同じであれば、常微分のときと同様に逆数にしてよい。たとえば、 \begin{equation} \PDC{x}{\rcol{r}}{\thetacol{\theta}} = {1\over \PDC{r}{\xcol{x}}{\thetacol{\theta}}}\label{koteionajitheta} \end{equation} （両辺ともに$\thetacol{\theta}$が一定）だし、 \begin{equation} \PDC{r}{\xcol{x}}{\ycol{y}} = {1\over \PDC{x}{\rcol{r}}{\ycol{y}}}\label{koteionaji} \end{equation} （両辺ともに$\ycol{y}$が一定）である。

　確認しよう。$\rcol{r},\thetacol{\theta}$が独立変数で$x\,\kakko{\rcol{r},\thetacol{\theta}}=\rcol{r}\cos \thetacol{\theta}$だから、 \begin{equation} \PDC{x\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}{\thetacol{\theta}}= \PDC{\left(\rcol{r}\cos \thetacol{\theta}\right)}{\rcol{r}}{\thetacol{\theta}}= \cos\thetacol{\theta}\label{partialrx} \end{equation} 右辺においては$\xcol{x},\thetacol{\theta}$が独立変数だから、分母を計算するには$r\,\kakko{\xcol{x},\thetacol{\theta}}={\xcol{x}\over \cos\thetacol{\theta}}$と表してから微分して \begin{equation} \PDC{r\,\kakko{\xcol{x},\thetacol{\theta}}}{\xcol{x}}{\thetacol{\theta}}= \PDC{\left({\xcol{x}\over \cos\thetacol{\theta}}\right)}{\xcol{x}}{\thetacol{\theta}}= {1\over \cos\thetacol{\theta}}\label{partialxr} \end{equation} である。

　同様に \begin{equation} \PDC{r\,\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}= \PDC{\sqrt{\xcol{x}^2+\ycol{y}^2}}{\xcol{x}}{\ycol{y}} ={\xcol{x}\over \sqrt{\xcol{x}^2+\ycol{y}^2}}={\xcol{x}\over \rcol{r}} \end{equation} 右辺の分母は、$\rcol{r}$と$\ycol{y}$を変数と考えての微分だから、$\xcol{x}$を$\rcol{r},\ycol{y}$で表した$x\,\kakko{\rcol{r},\ycol{y}}=\xcol{\pm}\sqrt{\rcol{r}^2-\ycol{y}^2}$（複号$\xcol{\pm}$は$\xcol{x}$が正なら$+$で、負なら$-$）という関数を偏微分する。すると、 \begin{equation} \PDC{x\,\kakko{\rcol{r},\ycol{y}}}{\rcol{r}}{\ycol{y}}= \xcol{\pm}\PDC{\sqrt{\rcol{r}^2-\ycol{y}^2}}{\rcol{r}}{\ycol{y}} =\xcol{\pm}{\rcol{r}\over\sqrt{\rcol{r}^2-\ycol{y}^2} }={\rcol{r}\over \xcol{x}} \end{equation} となり、この二つは逆数である。

${\partial z\over \partial y}{\partial y\over \partial x}\neq{\partial z\over \partial x}$

よくある誤り

　常微分の時に${\mathrm dz\over \mathrm dy}{\mathrm dy\over \mathrm dx}={\mathrm dz\over \mathrm dx}$ができたのだから偏微分でも$\PD{z}{\ycol{y}}\PD{y}{\xcol{x}}=\PD{z}{\xcol{x}}$だろう。

　これも、省略記法で書いているせいでこれでいいと勘違いしてしまうことがある。誤解がないよう省略なしで書けば、常微分の${\mathrm dz\over \mathrm dy}{\mathrm dy\over \mathrm dx}={\mathrm dz\over \mathrm dx}$は${\mathrm dz\kakko{\ycol{y}}\over \mathrm dy}{\mathrm dy\,\kakko{\xcol{x}}\over \mathrm dx}={\mathrm dz\kakko{y\,\kakko{\xcol{x}}}\over \mathrm dx}$である一方、偏微分の$\PD{z}{\ycol{y}}\PD{y}{\xcol{x}}\neq\PD{z}{\xcol{x}}$（等式ではないことに注意）は$\PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\PDC{y\,\kakko{\xcol{x},\zcol{z}}}{\xcol{x}}{\zcol{z}}\neq\PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$であり、本質的に違う計算である。

　教科書ではここで常微分の場合を示しているが、省略した。

　常微分が自由度１、つまり線の上しか動けないのに対し、偏微分の方は「$\xcol{x}$と$\ycol{y}$が決まると$\zcol{z}$が決まる（あるいはこの立場の入れ替え）」という関係だから自由度2で、2次元的広がり（曲面）の上を動ける（だから偏微分は方向の指定が必要になる）。

　2自由度の例として、$\xcol{x}^2+\ycol{y}^2+\zcol{z}^2=R^2$が成り立つ、すなわち3次元の中の球面（2次元的広がり）を考えよう。この条件を守りつつ、$\xcol{x},\ycol{y},\zcol{z}$を変化させる。その「変化の方向」は複数個ある。次の図には、$\xcol{x},\ycol{y},\zcol{z}$のうちどれか一つを固定しつつ動かすという三つの「変化の方向」を示した。

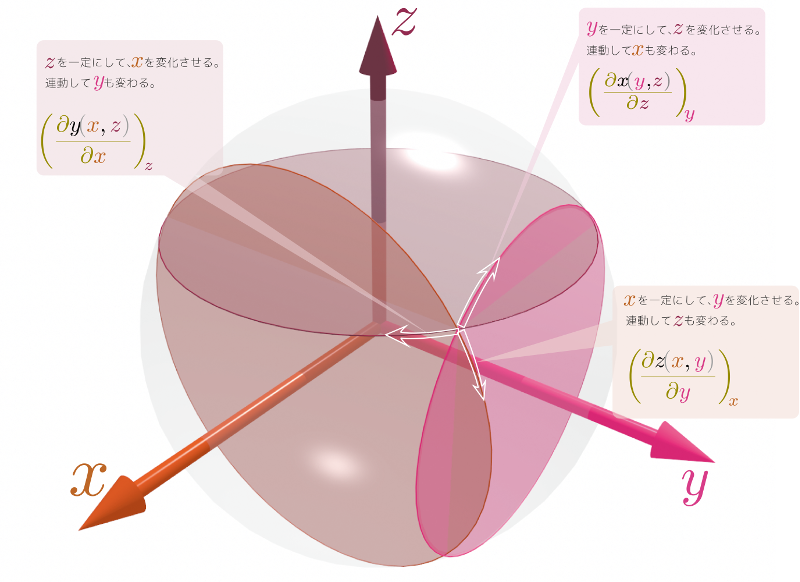
　この場合$\zcol{z}=\zcol{\pm}\sqrt{R^2-\xcol{x}^2-\ycol{y}^2}$とか$\ycol{y}=\ycol{\pm}\sqrt{R^2-\xcol{x}^2-\zcol{z}^2}$のような関係式がある二つの複号のうち、前の方の$\zcol{\pm}$は$\zcol{z}$が正か負かにより決まる。一方、後ろの$\ycol{\pm}$は$\ycol{y}$が正か負かで決まる。。微分を実行すると、 \begin{equation} \PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} ={\zcol{\mp}\ycol{y}\over \sqrt{R^2-\xcol{x}^2-\ycol{y}^2}},~~~~ % \PDC{y\,\kakko{\xcol{x},\zcol{z}}}{\xcol{x}}{\zcol{z}} \PDC{y\,\kakko{\xcol{x},\zcol{z}}}{\xcol{x}}{\zcol{z}} ={\ycol{\mp}\xcol{x}\over \sqrt{R^2-\xcol{x}^2-\zcol{z}^2}} \end{equation} である（微分でマイナス符号が出るので複号がひっくり返ることに注意）。

　この微分は別の計算方法もある。まず、最初の式$\xcol{x}^2+\ycol{y}^2+\zcol{z}^2=R^2$の独立変数を$\xcol{x},\ycol{y}$にすることで$\xcol{x}^2+\ycol{y}^2+\left(z\,\kakko{\xcol{x},\ycol{y}}\right)^2=R^2$としたのち、両辺を「$\xcol{x}$を一定にして$\ycol{y}$で微分」する。$\xcol{x}$は一定だから第1項の$\xcol{x}^2$の微分は0になり、$\ycol{y}^2$の微分は$2\ycol{y}$となり、結局$2\ycol{y}+2z\,\kakko{\xcol{x},\ycol{y}}\PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}=0$となる。これから、$\PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}=-{\ycol{y}\over z\,\kakko{\xcol{x},\ycol{y}}}$となる。これは$\PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}={\zcol{\mp}\ycol{y}\over \sqrt{R^2-\xcol{x}^2-\ycol{y}^2}}$と同じ式。

　この二つの掛算をし、$\ycol{\pm}\sqrt{R^2-\xcol{x}^2-\zcol{z}^2}=\ycol{y}$であることを使うと、 \begin{equation} \PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \PDC{y\,\kakko{\xcol{x},\zcol{z}}}{\xcol{x}}{\zcol{z}} ={\zcol{\mp}\ycol{y}\over \sqrt{R^2-\xcol{x}^2-\ycol{y}^2}}\times\gunderbrace{{\ycol{\mp}\xcol{x}\over \sqrt{R^2-\xcol{x}^2-\zcol{z}^2}}}_{{\ycol{\pm}\ycol{y}}} ={\zcol{\pm}\xcol{x} \over \sqrt{R^2-\xcol{x}^2-\ycol{y}^2}} \end{equation} となる。一方、$\PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} ={\zcol{\mp}\xcol{x}\over \sqrt{R^2-\xcol{x}^2-\ycol{y}^2}}$ だから、この二つの式から \begin{equation} \PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \PDC{y\,\kakko{\xcol{x},\zcol{z}}}{\xcol{x}}{\zcol{z}} = - \PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\label{henbibunminus} \end{equation} \begin{equation} \PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \PDC{y\,\kakko{\xcol{x},\zcol{z}}}{\xcol{x}}{\zcol{z}} \PDC{x\,\kakko{\ycol{y},\zcol{z}}}{\zcol{z}}{\ycol{y}}=-1\label{henbibuntimesminus} \end{equation} という関係になっている（右辺のマイナス符号に注意！）。

　こういうのは自分でやってみて納得するのが一番なので、$\xcol{x},\ycol{y},\zcol{z}$の間に適当な関係式（なんでもよい）を作り、その場合で上の式が成立することを確認しよう（納得いくまで、いろいろ試してみることを勧める）。

　この式は$z\,\kakko{\xcol{x},\ycol{y}}$などが微分可能である限り正しい。以下で一般的に示していこう。まず数式を使って示そう（後で図解する）。

　$\xcol{x},\ycol{y},\zcol{z}$という3次元の空間を考える。ある関係式（上の例では$\xcol{x}^2+\ycol{y}^2+\zcol{z}^2=R^2$）により、三つの変数のうち一つを他の二つで表すことができるつまり、自由度2である。我々は三つの変数の中から2個を選んで計算を行うことになる。としよう。すなわち \begin{equation} \xcol{x}=X\kakko{\ycol{y},\zcol{z}},~ \ycol{y}=Y\kakko{\xcol{x},\zcol{z}},~ \zcol{z}=Z\kakko{\xcol{x},\ycol{y}} \end{equation} という三つの式（上の例では$\zcol{z}=\zcol{\pm}\sqrt{R^2-\xcol{x}^2-\ycol{y}^2}$など）を作ることができたものとしよう。第３の式に第２の式を代入すると、 \begin{equation} \zcol{z}=Z\kakko{\xcol{x},Y\kakko{\xcol{x},\zcol{z}}}\label{zz} \end{equation} という式ができる。この段階で、$\ycol{y}$という変数は消えて、$Y\kakko{\xcol{x},\zcol{z}}$という関数に置き換えられたので、変数は$\xcol{x},\zcol{z}$の二つである。計算の結果、この式\式{zz}は$\zcol{z}=\zcol{z}$という当たり前の式に戻る筈である。

　上の例の$\zcol{z}=\zcol{\pm}\sqrt{R^2-\xcol{x}^2-\ycol{y}^2}$に$\ycol{y}=\ycol{\pm}\sqrt{R^2-\xcol{x}^2-\zcol{z}^2}$を代入してみると、 \begin{equation} \zcol{z}=\zcol{\pm}\sqrt{R^2-\xcol{x}^2-(R^2-\xcol{x}^2-\zcol{z}^2)}=\zcol{\pm}\sqrt{\zcol{z}^2}=\zcol{z}\label{zzkekka} \end{equation} となって、$\zcol{z}=\zcol{z}$になる（もともと複号$\zcol{\pm}$は$\zcol{z}$が正なら$+$で、負なら$-$だったから、右辺は$\zcol{z}$にしてよい）。

　つまり、この式の右辺は$\xcol{x}$を含んでいるように見えるが、実は含んでいない。ここで、両辺を「$\zcol{z}$を一定として$\xcol{x}$で微分」する。計算するまでもなく（$\zcol{z}$を一定としているのだから）左辺の微分は0である。一方、右辺は$\xcol{x}$が２箇所にあることから微分の結果は二つの式の和となり、結果が0となる（二つの項が打ち消す）。すなわち、

$0=\goverbrace{\PDC{Z\kakko{\xcol{x},\thetacol{Y}}}{\xcol{x}}{\thetacol{Y}}}^{左の\xcol{x}を微分}+\goverbrace{\PDC{Z\kakko{\xcol{x},\thetacol{Y}}}{\thetacol{Y}}{\xcol{x}}\PDC{{Y}\kakko{\xcol{x},\zcol{z}}}{\xcol{x}}{\zcol{z}}}^{右の\xcol{x}を微分}$

が導かれる。

　教科書ではここで別の数式による証明があるが、そこは飛ばしたので各自読んで検算してみること。

　以上は計算による導出だが、次に図解を試みよう。

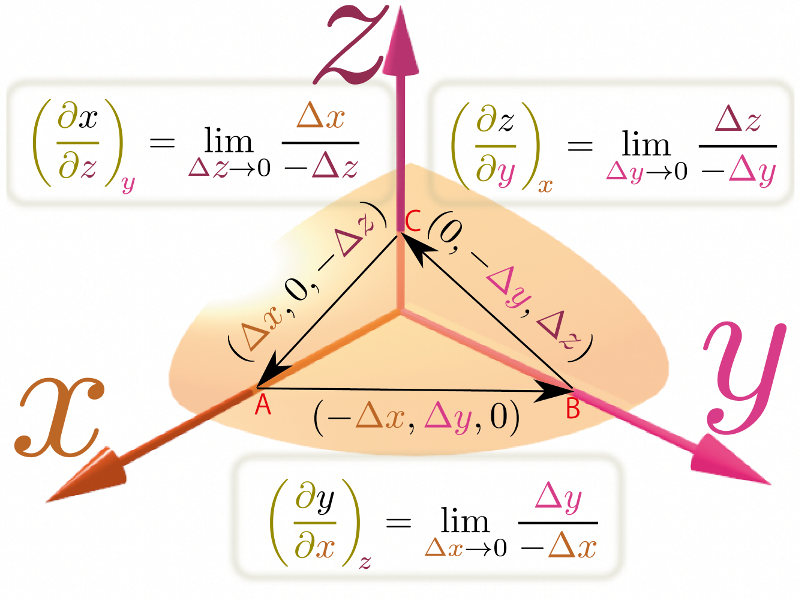
　上の図は三つの変数$\xcol{x},\ycol{y},\zcol{z}$の間にある関係式があり、三つの変数が図に示したある曲面の上に制限されている様子を示すここでは簡単のため原点付近で考えることにするが、場所に依らず、どこで考えても同様のことが言える。。この変数の間の関係式を成立させつつ（つまり曲面から離れないように）、

$\zcol{z}$を一定として$\xcol{x}$を変化（連動して$\ycol{y}$も変化）。
$\xcol{x}$を一定として$\ycol{y}$を変化（連動して$\zcol{z}$も変化）。
$\ycol{y}$を一定として$\zcol{z}$を変化（連動して$\xcol{x}$も変化）。

という三つの変化を考える。これらの変化は図の点A$(\xcol{\Delta x},0,0)$から点B$(0,\ycol{\Delta y},0)$と点C$(0,0,\zcol{\Delta z})$ここでの$\xcol{\Delta x}$は$\xcol{x}$の変化量ではなく、点Aが原点からどれだけ離れているかを示すパラメータ（$\ycol{\Delta y},\zcol{\Delta z}$も同様）。を通過し点Aに戻ってくる経路をなす。

　それぞれの過程において図に描き込んだような分数を計算し、その掛算を行うと、 \begin{equation} {\zcol{\Delta z}\over -\ycol{\Delta y}}\times {\xcol{\Delta x}\over -\zcol{\Delta z}}\times {\ycol{\Delta y}\over -\xcol{\Delta x}}=-1 \end{equation} となる（分母分子に同じものが２回ずつ現れ、分母にマイナスが３回現れる）。$\xcol{\Delta x},\ycol{\Delta y},\zcol{\Delta z}$をすべて$\to0$とする極限を取ればこれは \begin{equation} \PDC{z\,\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\PDC{x\,\kakko{\ycol{y},\zcol{z}}}{\zcol{z}}{\ycol{y}}\PDC{y\,\kakko{\xcol{x},\zcol{z}}}{\xcol{x}}{\zcol{z}}=-1 \label{PPPminusone} \end{equation} を意味する。

　この符号の違いを、「常微分なら$+$で偏微分なら$-$」などと機械的に覚える---ことは絶対しないように。

　偏微分でも、固定する変数が違わなければマイナス符号は出ない。たとえば$\PDC{f}{\zcol{z}}{\xcol{x}}\times \PDC{z}{\ycol{y}}{\xcol{x}}=\PDC{f}{\ycol{y}}{\xcol{x}}$である。「なぜこうなるのか（符号がつくのか）」という本質を理解すべし。

偏微分の注意点