2次元の座標系
2次元以上の座標系と微分
2次元の座標
2次元の直交座標
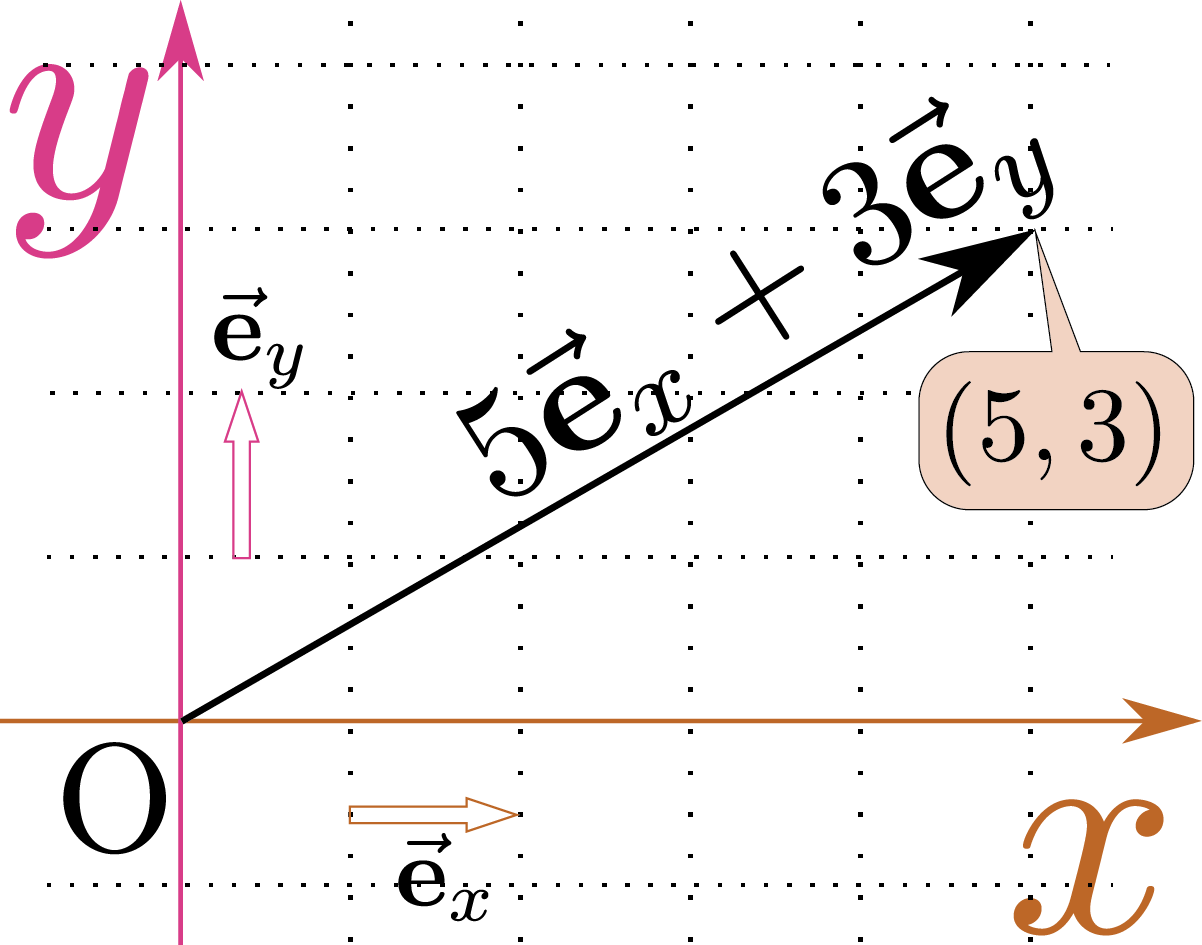
平面上の位置は、原点からその場所に引っ張った矢印であるベクトル(位置ベクトル)$\colvecx=\xcol{x}\ve_x+\ycol{y}\ve_y$を使って「$\colvecx$」のように$x$にベクトル記号をつけて位置ベクトルを表すのが慣習であるが、こう書いたからといって$\ycol{y}$成分のことを考えていないわけではないことに注意。なお、位置ベクトルを$\rcol{\vec r}$のように$r$を使って表現することも多い。表現できる。位置ベクトルを$\colvecx=\xcol{x}\ve_x+\ycol{y}\ve_y$のように書いたが、単位ベクトルの前の係数(「ベクトルの成分」と呼ぶ)を括弧の中に並べて$(\xcol{x},\ycol{y})$と書いてもよい。位置ベクトルをこう表現したとき、$\xcol{x}$と$\ycol{y}$という二つの数を指定すれば位置が一つ決まることになる。この「位置を表現する数」が「座標」である。上の$\xcol{x}$と$\ycol{y}$はもっともよく使われる座標の例で、この組$(\xcol{x},\ycol{y})$を「直交座標」本書での「直交座標」は英語で「rectangular coordinate」。「直交座標」を直訳すると「orthogonal coordinate」になるが、これは本書で言う「直交曲線座標」の意味で用いられることが多い(厳密な区別をしてない本も多い)。または「デカルト座標(Cartesian coordinate)」「Cartesian」は「デカルト(Descartes、ラテン語化してCartesius)の」という意味。と呼ぶ。図の場合の(5,3)は「原点を出発点として$\xcol{x}$軸方向に5、$\ycol{y}$軸方向に3だけ移動した場所」を意味する。5と3という二つの座標が位置を表すわけである。
3次元直交座標(ここではまだ2次元を扱っているが)の「$\xcol{x},\ycol{y},\zcol{z}$方向を向いた単位ベクトル」を本書では$\ve_x,\ve_y,\ve_z$と表現している(後で出てくる極座標では$\ve_r,\ve_\theta,\ve_\phi$を使う)。他に、${\mathbf e}_x,{\mathbf e}_y,{\mathbf e}_z$(矢印をつけない)と書いたり、${\mathbf i},{\mathbf j},{\mathbf k}$という文字を使ったり、$\hat {\mathbf x},\hat {\mathbf y},\hat {\mathbf z}$のようにハット$\hat {~}$をつける(後で出てくる極座標では$\hat {\mathbf r},\hat{\theta},\hat{\phi}$を使う)などの書き方をしている本もある。
$5\ve_x+4\ve_y-7\ve_z$、$5{\mathbf i}+4{\mathbf j}-7{\mathbf k}$、$5\hat x+4\hat y-7\hat z$はすべて成分$(5,4,-7)$を持つベクトルで、記号が違っても中身は変わらない。
それぞれの点に応じて一つの数が決まる対応関係がある場合、その対応関係すなわち関数を$f\kakko{\xcol{x},\ycol{y}}$または$f\kakko{\!\colvecx\!}$と書く。$f\kakko{\!\colvecx\!}$と書いたからといって、関数$f$がベクトルになったわけではない。$f\kakko{\!\colvecx\!}$は「ベクトル$\colvecx$を一個決めると数$f\kakko{\!\colvecx\!}$が決まる」という関係である。
以下では、座標と別の座標の間の変換(座標変換)について考えていく。
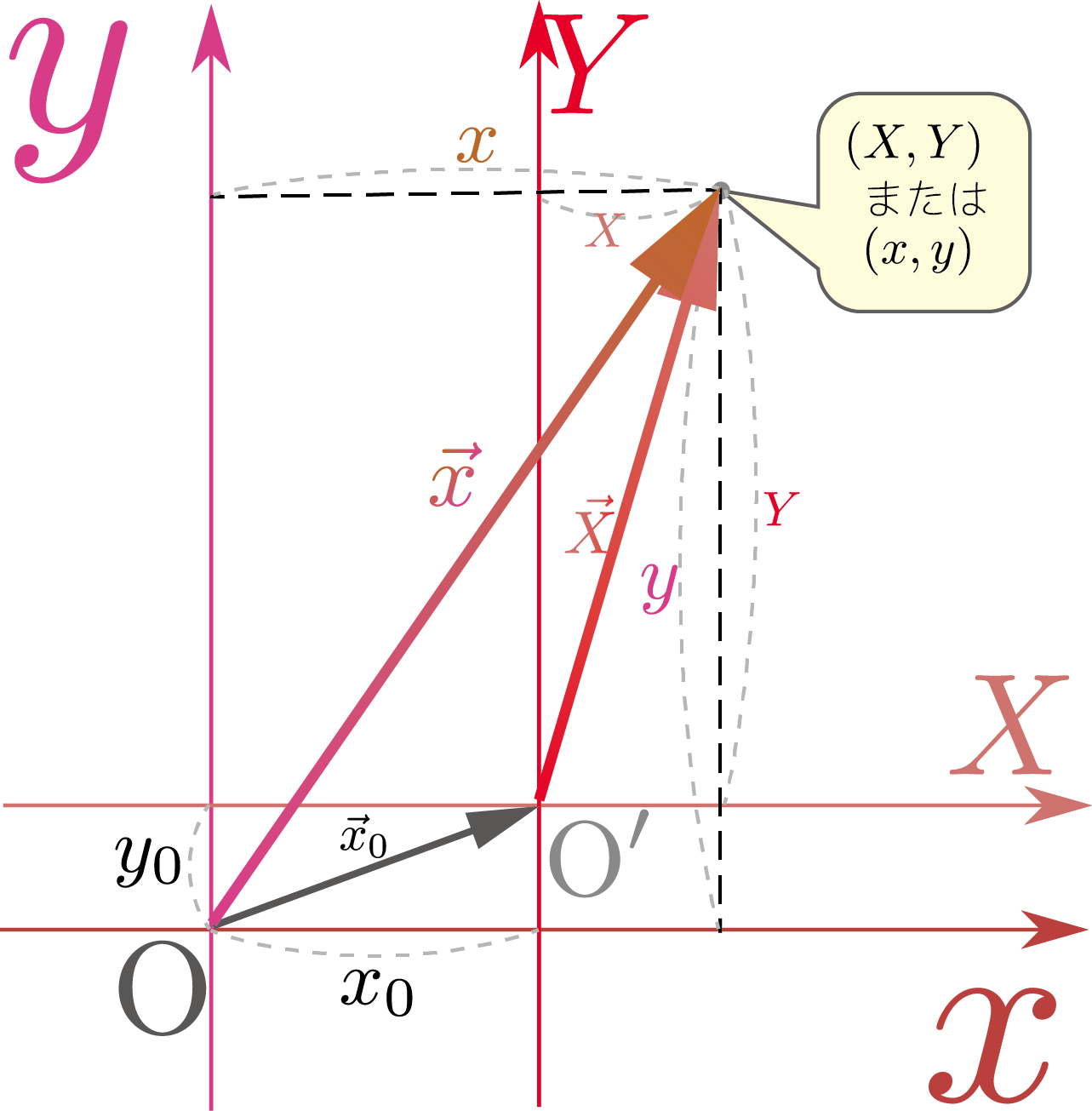
直交座標から別の直交座標への変換
まず座標軸の向きを変えずに座標の原点を取り直すという変換、すなわち平行移動を考えよう。それは右の図に示したような直交座標$(\xcol{x},\ycol{y})$から直交座標$(\zcol{X},\thetacol{Y})$への変換で、 \begin{equation} \begin{array}{rl} \zcol{X}=&\xcol{x}-x_0\\ \thetacol{Y}=&\ycol{y}-y_0 \end{array}\label{XYxyheikou} \end{equation} のような式で表される。ベクトルの式で書くと、 \begin{equation} \goverbrace{\zcol{X}\ve_X+\thetacol{Y}\ve_Y}^{\zcol{\vec X}}=\goverbrace{\xcol{x}\ve_x+\ycol{y}\ve_y}^{\colvecx}-\goverbrace{\left(x_0\ve_x+y_0\ve_y \right)}^{\vec x_0}\label{heikouidouvector} \end{equation} となる。原点の平行移動はプラス方向だが、座標変換の式は引算になることに注意しよう。こうすることで、$\xcol{x}=x_0,\ycol{y}=y_0$で表される点と$\zcol{X}=0,\thetacol{Y}=0$で表される点が同一点(どちらも図の点${\rm O'}$)になる。
次に、原点は等しいが軸の向きが$\alpha$だけ違う直交座標と直交座標との変換を考えてみよう。
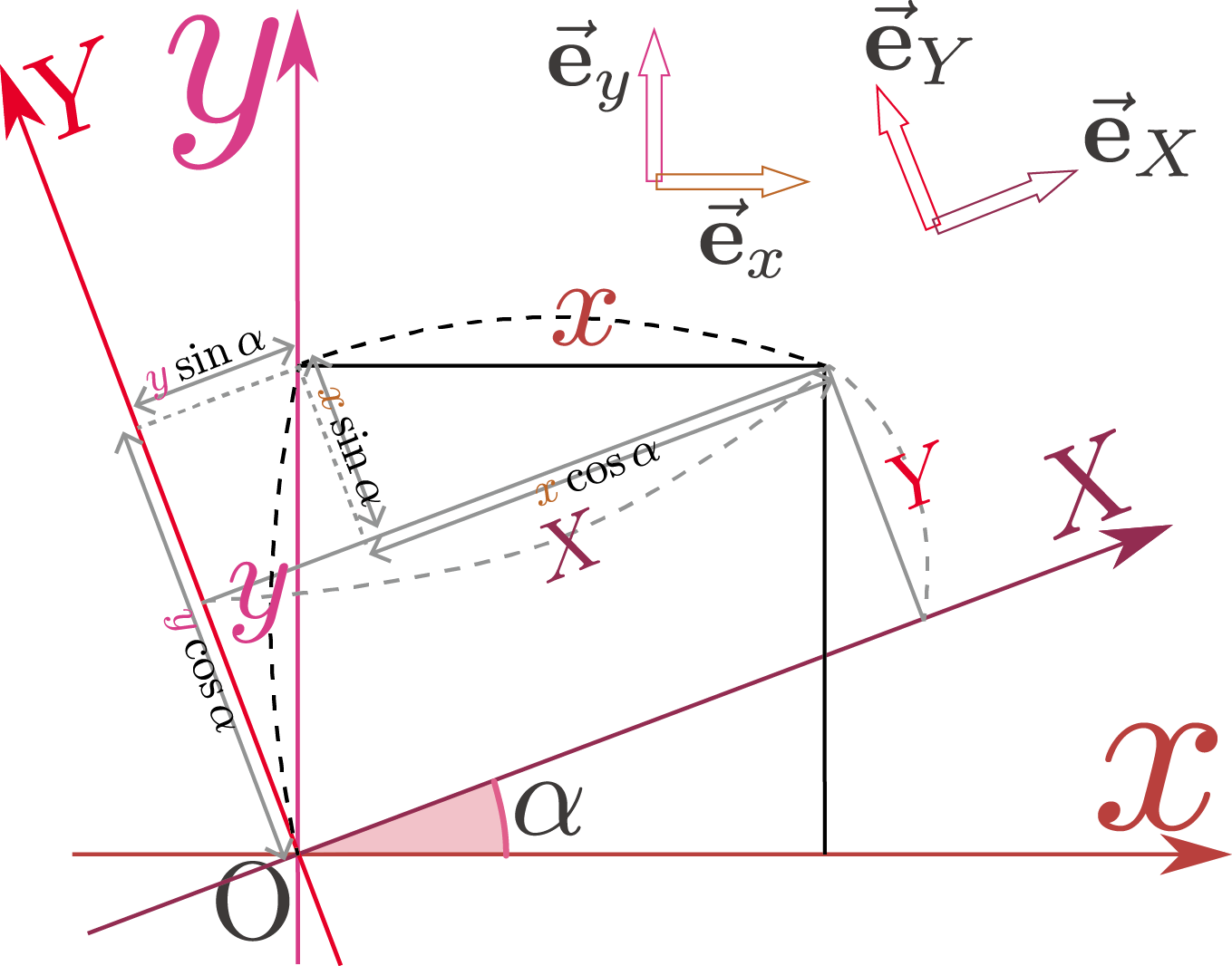
上の図を見て座標の関係を考えるとわかるように、 \begin{equation} \begin{array}{rl} \zcol{X}=&\xcol{x}\cos\alpha+\ycol{y}\sin \alpha \\ \thetacol{Y}=&-\xcol{x}\sin\alpha+\ycol{y}\cos \alpha \end{array}\label{XYxy} \end{equation} が座標変換の式となる。この式を少し計算上の式$\times\cos\alpha$から下の式$\times\sin \alpha$を引くと出せる。もしくは上と同様に図を描いて考えることで、 \begin{equation} \begin{array}{rl} \xcol{x}=&\zcol{X}\cos\alpha-\thetacol{Y}\sin \alpha \\ \ycol{y}=&\zcol{X}\sin\alpha+\thetacol{Y}\cos \alpha \end{array}\label{xyXY} \end{equation} という逆関係を得るこの二つが逆関係なのは、$(\xcol{x},\ycol{y})$から$(\zcol{X},\thetacol{Y})$への回転と$(\zcol{X},\thetacol{Y})$から$(\xcol{x},\ycol{y})$への回転の「回転角度」が逆になると考えてもわかる。。
行列をすでに知っている人は \begin{equation}\left( \begin{array}{c}\zcol{X}\\\thetacol{Y}\end{array}\right)=\left(\begin{array}{cc}\cos \alpha&\sin \alpha\\-\sin \alpha&\cos \alpha\end{array}\begin{array}{c}\xcol{x}\\\ycol{y}\end{array}\right),~~~ \left(\begin{array}{c}\xcol{x}\\\ycol{y}\end{array}\right) =\left(\begin{array}{cc}\cos \alpha&-\sin \alpha\\\sin \alpha&\cos \alpha\end{array}\right)\left(\begin{array}{c}\zcol{X}\\\thetacol{Y}\end{array}\right) \end{equation} のような行列計算で考えてもよい。ここに現れた二つの行列は互いの逆行列である。
どちらの座標系でも位置ベクトルそのものは等しいので、以下の式が成り立つ。 \begin{equation} \zcol{X}\ve_X+\thetacol{Y}\ve_Y=\xcol{x}\ve_x+\ycol{y}\ve_y \end{equation} ここで$\ve_X,\ve_Y$はそれぞれ$\zcol{X}$軸方向と$\thetacol{Y}$軸方向を向いた単位ベクトルである。 平行移動の場合は原点のずれの分の差が生じたが、回転の場合はベクトルは同じで成分の表現が異なる。
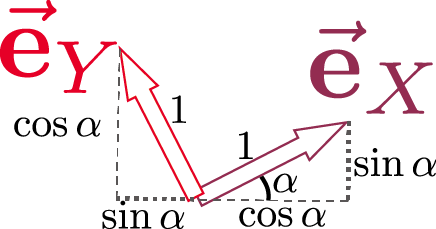
上の図から読み取れるように、$\ve_X,\ve_Y$は \begin{equation} \ve_{X}=\cos\alpha\ve_x+\sin \alpha\ve_y,~~~~~ \ve_{Y}=-\sin\alpha\ve_x+\cos \alpha\ve_y\label{eXYexy} \end{equation} のように$\ve_x,\ve_y$と関係している。代入して \begin{equation} \begin{array}{rl} \zcol{X}\gunderbrace{\left(\cos\alpha\ve_x+\sin \alpha\ve_y\right)}_{\ve_X}+\thetacol{Y}\gunderbrace{\left(-\sin\alpha\ve_x+\cos \alpha\ve_y\right)}_{\ve_Y} =& \gunderbrace{\left(\zcol{X}\cos\alpha-\thetacol{Y}\sin \alpha\right)}_{\xcol{x}}\ve_x + \gunderbrace{\left(\zcol{X}\sin\alpha+\thetacol{Y}\cos \alpha\right)}_{\ycol{y}}\ve_y \end{array} \end{equation} のように計算すると、確かに二つのベクトルが等しいことが確認できる。
直交座標から直交座標への変換では、この他にも反転$\zcol{X}=-\xcol{x},\thetacol{Y}=\ycol{y}$などがある。
2次元の極座標
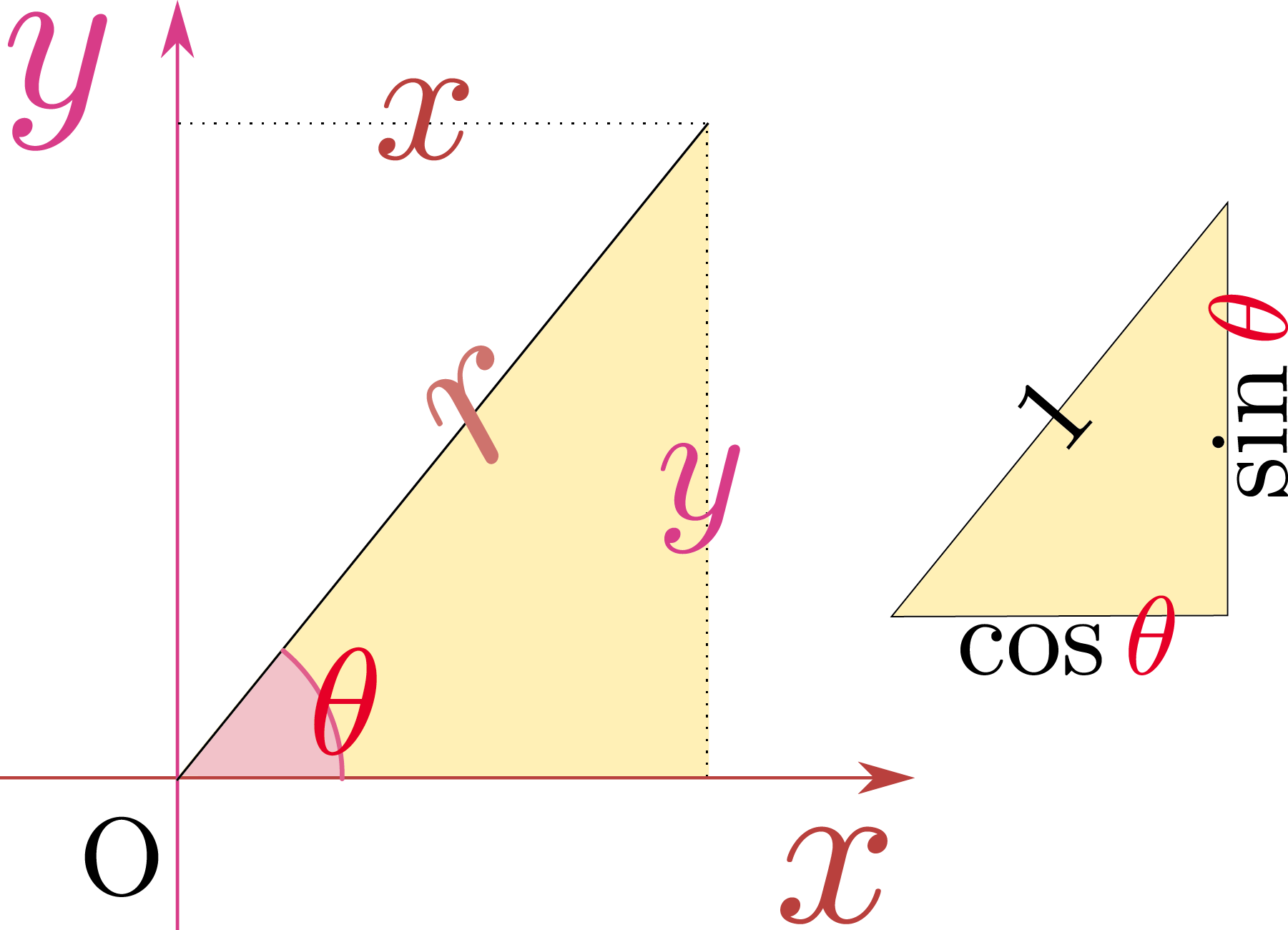
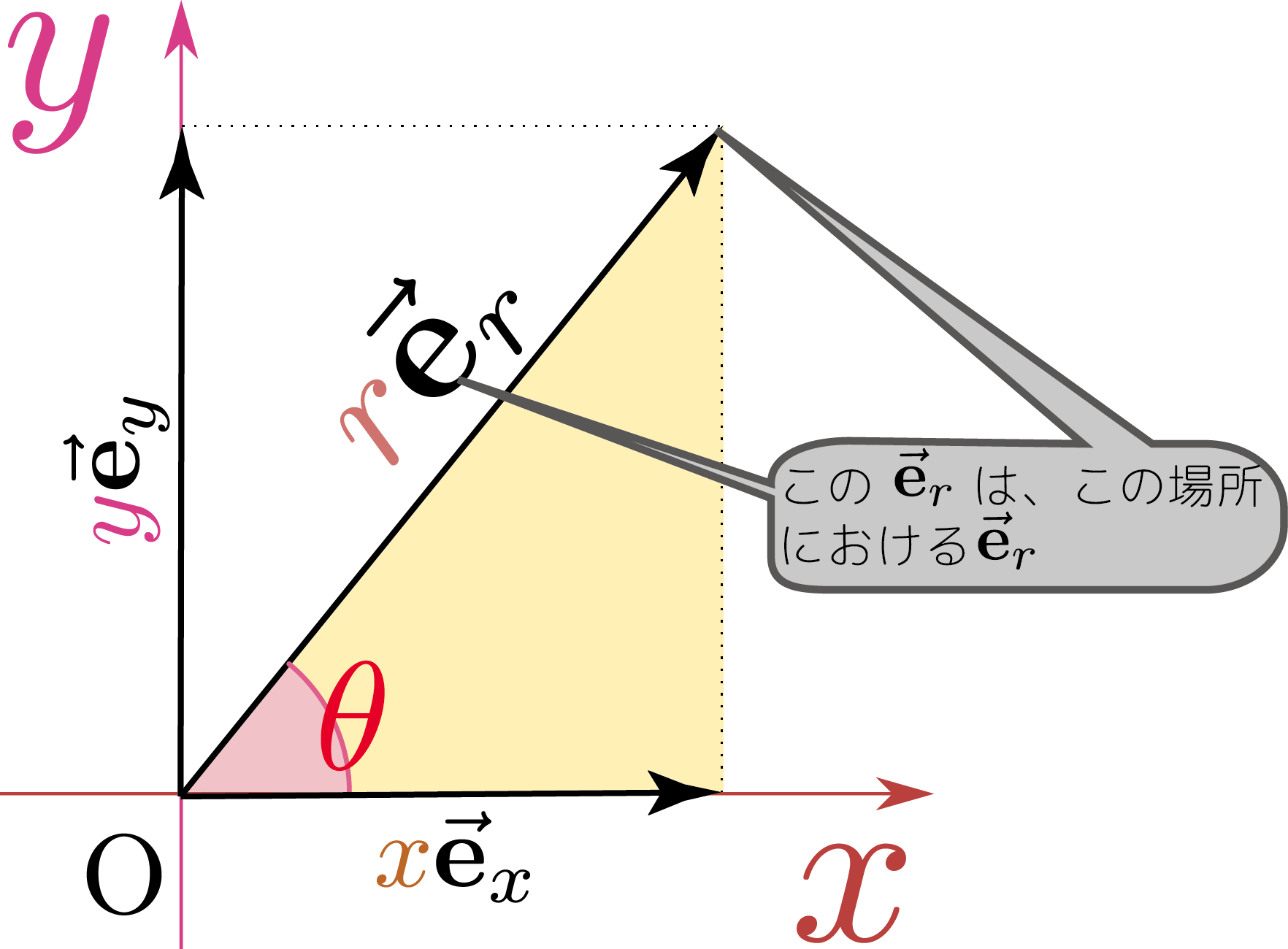
直交座標の他にもう一つよく使われるのが極座標で、原点からの距離$\rcol{r}=\sqrt{\xcol{x}^2+\ycol{y}^2}$と、どの方向に原点から離れているかを表す角度$\thetacol{\theta}$で位置を表現するその意味からして、$\rcol{r}=0$(原点)では$\thetacol{\theta}$座標が無意味になることに注意。これを「原点は極座標の特異点である」という言い方をする。。図からわかるように極座標と直交座標には以下のような関係がある。 \begin{equation} \begin{array}{ll} \xcol{x}=\rcol{r}\cos \thetacol{\theta},~~~~&\ycol{y}=\rcol{r}\sin \thetacol{\theta},\\[2mm] \rcol{r}=\sqrt{\xcol{x}^2+\ycol{y}^2},\\ \cos\thetacol{\theta}={\xcol{x}\over \sqrt{\xcol{x}^2+\ycol{y}^2}},~~~&\sin\thetacol{\theta}={\ycol{y}\over \sqrt{\xcol{x}^2+\ycol{y}^2}} \end{array} \end{equation}
$\xcol{x},\ycol{y}$はどちらも実数全体$-\infty$から$\infty$が定義域だが、極座標では$0\leq \rcol{r}<\infty$(0以上の数のみ)と$0\leq\thetacol{\theta}<2\pi$となる。$\thetacol{\theta}<2\pi$にしたのは$\thetacol{\theta}=2\pi$にあたる点は$\thetacol{\theta}=0$と同じ点であるからだが、座標に重複を許すならば$-\infty<\thetacol{\theta}<\infty$(定義域は実数全体)としてもよい。その場合、$\thetacol{\theta}$という座標が$\thetacol{\theta}$と$\thetacol{\theta}+2n\pi$($n$は整数)は同一点という周期性を持つ点に注意が必要である。
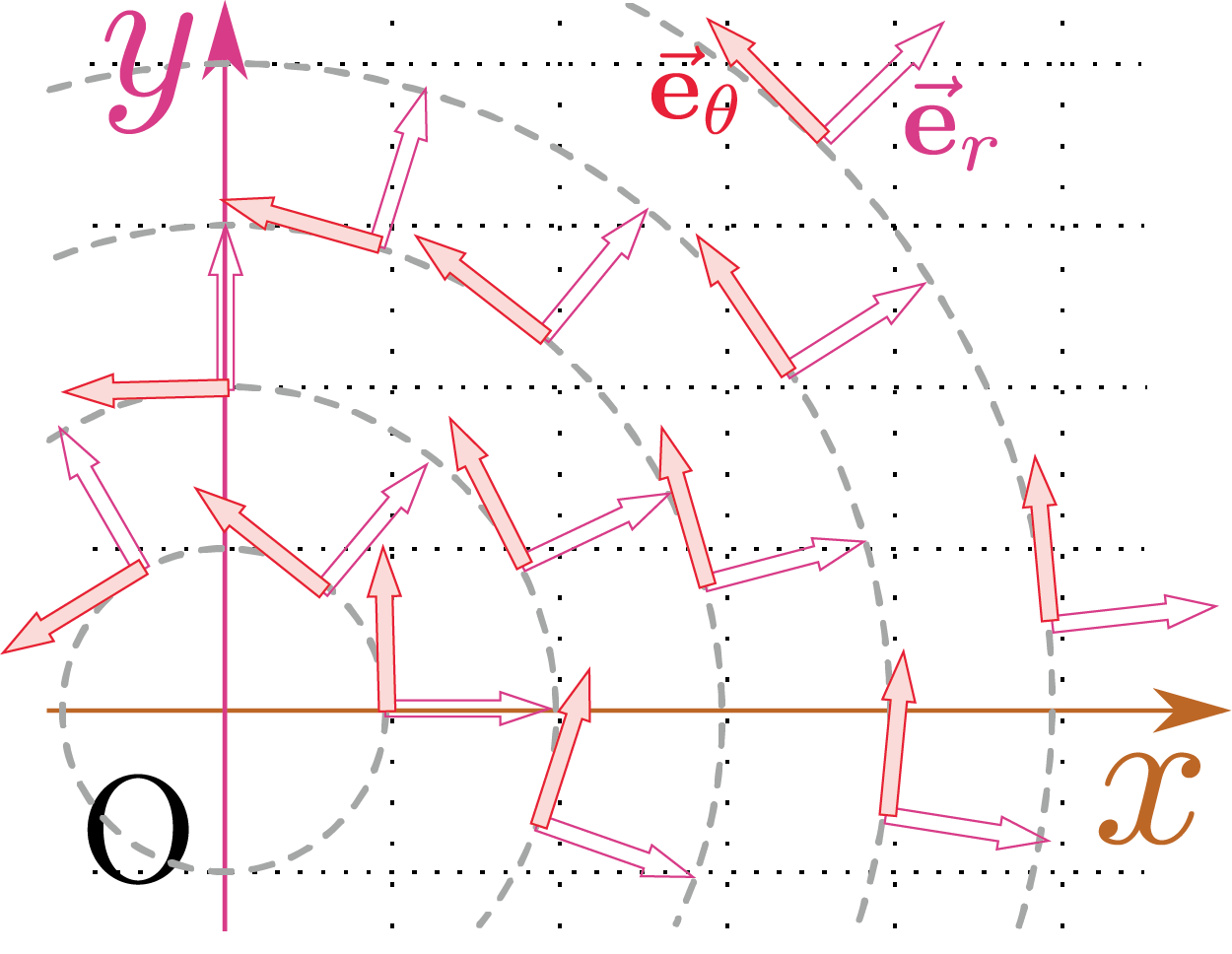
直交座標の$\ve_x,\ve_y$同様、極座標でも$\rcol{r}$方向($\rcol{r}$が増加する方向)の単位ベクトル、$\thetacol{\theta}$方向($\thetacol{\theta}$が増加する方向)の単位ベクトルを考えて、これを$\ve_r,\ve_\theta$と書く(${\bf \hat r},{\bf \hat \theta}$と書いている本もある)。図に表したように(そして、その定義から当然そうなるべく)、$\ve_r,\ve_\theta$は場所によって違う方向を向く原点においては、$\ve_\theta$は定義できない(そもそも$\thetacol{\theta}$が定義できない)。また、原点においては$\ve_r$はすべての方向、どちらを向いてもよいことになる。この意味でも原点は特異点である。。具体的に言えば$\thetacol{\theta}$によって違う方向を向くので、$\thetacol{\theta}$の関数座標$\thetacol{\theta}$を決めるとベクトルが一つ決まる。数→ベクトルという関数。である。そう考えるならば$\ve_r,\ve_\theta$は「$\ve_r\kakko{\thetacol{\theta}},\ve_\theta\kakko{\thetacol{\theta}}$」のように、$\thetacol{\theta}$の関数であることを明示すべきである(しかししばしば省略する)。
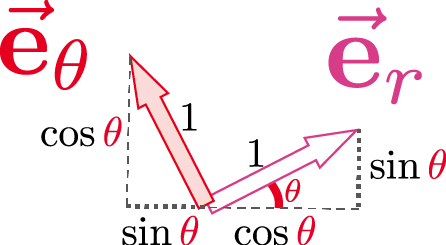
同様に下の図のように考えると(\ref{eXYexy})のときと違って、角度 $\thetacol{\theta}$は変数であり、場所によって違う。極座標のベクトルを考えるときはこの点に注意しよう。$\ve_r$は$\xcol{x}$成分が$\cos\thetacol{\theta}$で$\ycol{y}$成分が$\sin\thetacol{\theta}$なので、 \begin{equation} \ve_r\kakko{\thetacol{\theta}}=\phantom{-}\cos\thetacol{\theta}\ve_x+\sin\thetacol{\theta}\ve_y \end{equation} となる。同様に$\ve_\theta$は$\xcol{x}$成分が$-\sin\thetacol{\theta}$で$\ycol{y}$成分が$\cos\thetacol{\theta}$となり \begin{equation} \ve_\theta\kakko{\thetacol{\theta}}=-\sin \thetacol{\theta}\ve_x+\cos\thetacol{\theta}\ve_y \end{equation} と書ける(当然$\thetacol{\theta}$に依存する)。この二つのベクトルは直交する($\ve_r\kakko{\thetacol{\theta}}\cdot\ve_\theta\kakko{\thetacol{\theta}}=0$)。以上がいろんな$\thetacol{\theta}$のときに正しいことは、図をたくさん描いて確認して欲しい。
$\ve_r\cdot\ve_\theta=0$は、極座標の「$\rcol{r}$方向」と「$\thetacol{\theta}$方向」が直交していることを示す。「直交座標」という言葉を「座標の方向が直交している座標系」と捉えるならば、極座標も“直交座標”だということになる。本書では「直交座標」はデカルト座標系$(\xcol{x},\ycol{y})$の名前として使うことにして、「座標の方向が直交している座標系」は「直交曲線座標(orthogonal coordinate)」と呼ぶことにする。