2次元の座標と偏微分
2次元の方向微分
多変数関数のもっともよく出てくる例は「2次元(面)上や3次元(立体)内の場所に依存する関数」である。そこでこの節ではまず$\xcol{x},\ycol{y}$という2次元平面上の関数とその微分について考える。
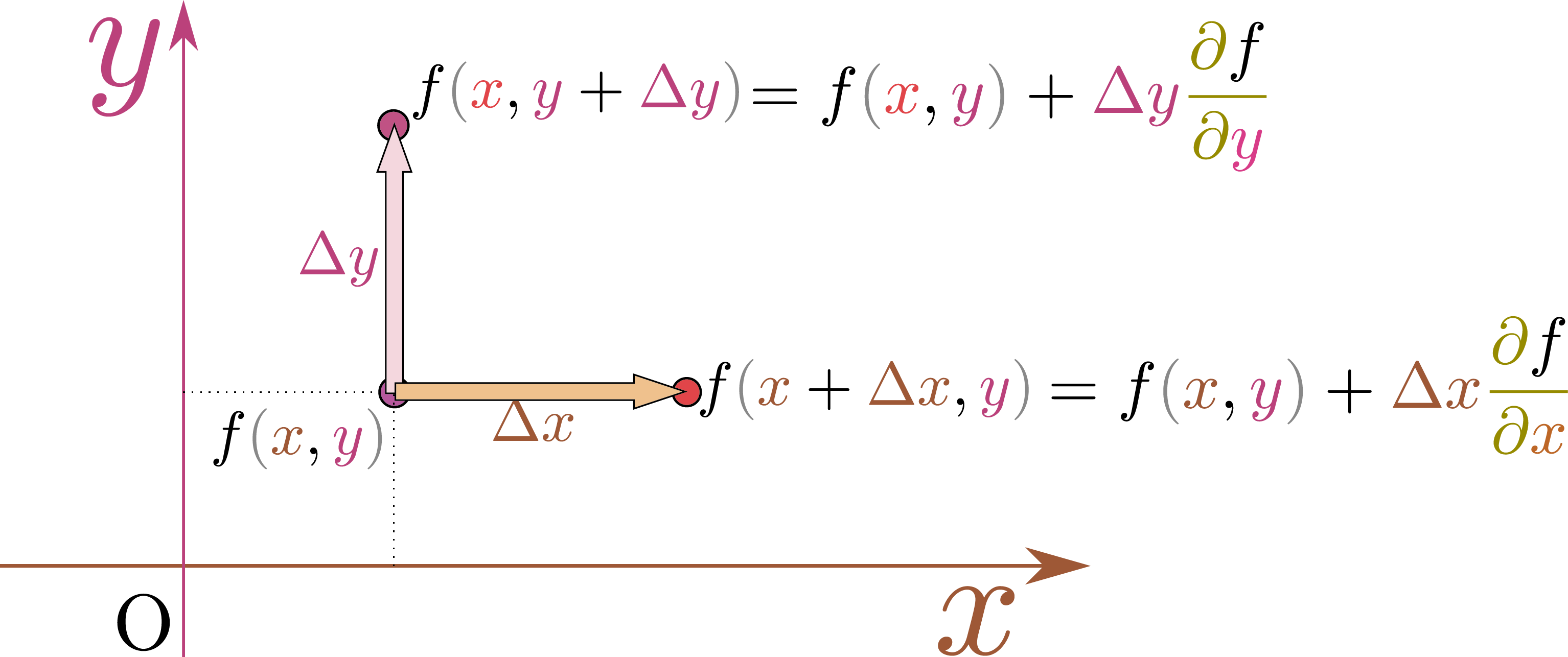
まずは$\xcol{x},\ycol{y}$という2変数の「座標」の関数の場合で話をする。$f\kakko{\xcol{x},\ycol{y}}$の「偏微係数(偏導関数)」は$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$と$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}$の二つがあった。この二つはそれぞれ、「$\xcol{x}$方向に移動した場合」「$\ycol{y}$方向に移動した場合」の微小変化の割合であった。
微分は「独立変数の変化に対する従属変数の変化の割合」なのだから、独立変数の変化のさせ方として「斜めに移動した場合」を考えて微分を行ってもよいではないか、と考えるのは当然である。
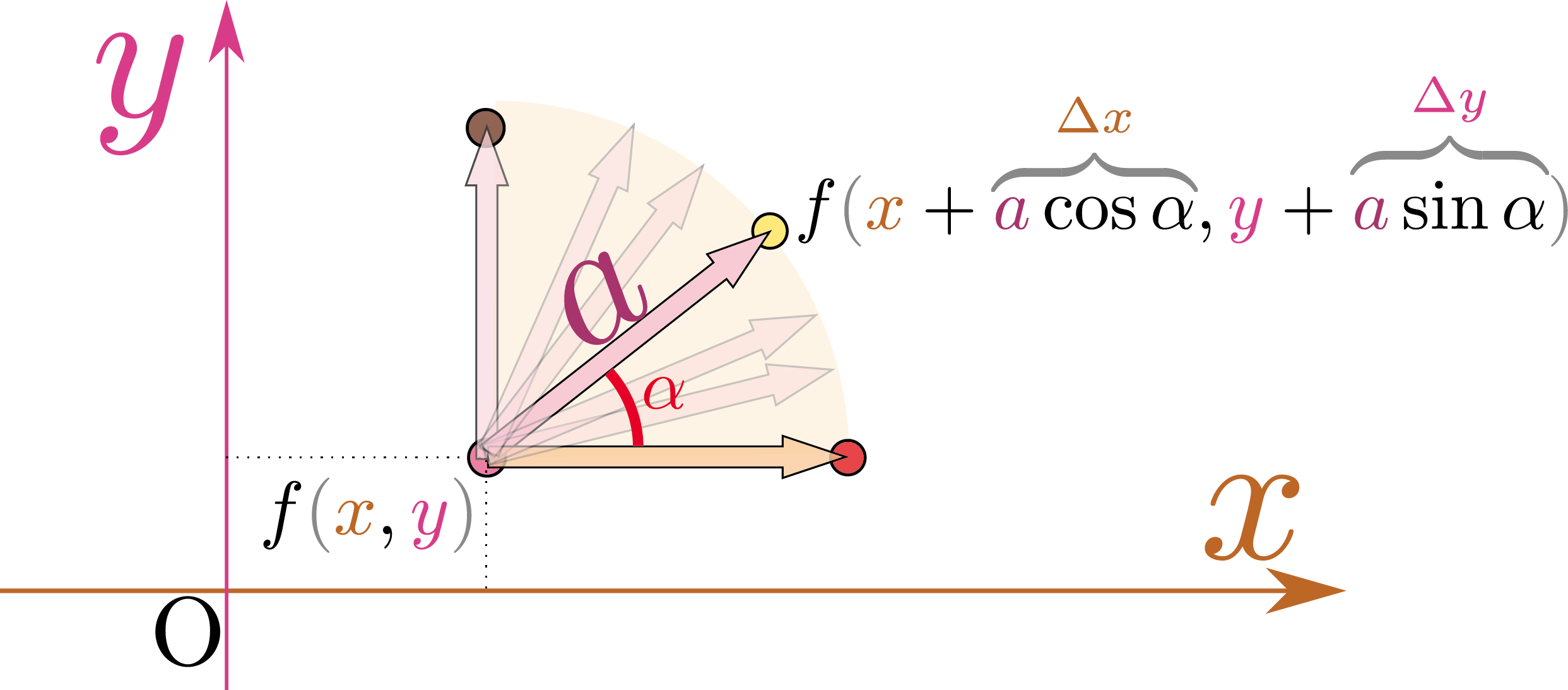
そこで、上の図のように傾いた方向に$\tcol{a}$だけ動いた場合の変化を考えよう。つまり、$\xcol{\Delta x}=\tcol{a}\cos\alpha,\ycol{\Delta y}=\tcol{a}\sin \alpha$と選ぶわけである。こうしておいて$f$の変化量を計算したのち、結果を移動量(今の場合$\tcol{a}$)で割ってから極限を取ると、 \begin{equation} \lim_{\tcol{a}\to0}{ f\kakko{\xcol{x}+ \goverbrace{\tcol{a}\cos\alpha}^{\xcol{\Delta x}},\ycol{y}+\goverbrace{\tcol{a}\sin\alpha}^{\ycol{\Delta y}}}-f\kakko{\xcol{x},\ycol{y}}\over \tcol{a} } =\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} \cos\alpha +\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \sin\alpha\label{houkoubibun} \end{equation} となる。この式は$\alpha=0$なら$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$($\alpha={\pi\over 2}$なら、$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}$)になる。$\xcol{x}$軸と角度$\alpha$を持った方向に移動したときの変化の割合を示すもので、「方向微分(directional derivative)」と呼ぶ。2次元ベクトルの内積の定義$\vec A\cdot\vec B=A_xB_x+A_yB_y$を思い出すと、上の式は二つのベクトル$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\ve_x+\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\ve_y$と$\ve_\alpha=\cos \alpha\ve_x+\sin \alpha\ve_y$の内積である、とも言える。よって、先に$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\ve_x+\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\ve_y$を求めておけば後で$\ve_\alpha$と内積を取ることであらゆる方向微分が計算できる。今後もよく使うので名前をつけよう。このベクトルを「$f$の勾配(gradient)」と名付け、「$\vgrad{f}$」$\vgrad{f}$は演算子で結果がベクトル。そこで本書では薄く矢印を上に付けている。また薄く関数を表す括弧をつけているが、通常は矢印も括弧もつけない。これは言わば「自転車の補助輪」のようなものと理解して、この本を読み終わる頃には矢印がついてなくても、「$\vgrad{f}$(通常の表記では${\rm grad}~f$)はベクトルだ」という感覚を身につけていて欲しい。と表す。記号「grad」は「グラディエント」と読む。
gradient(勾配)の定義
\begin{equation} \vgrad{f\kakko{\xcol{x},\ycol{y}}}=\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\ve_x + \PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\ve_y\label{defgrad} \end{equation}
この式を \begin{equation} \PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\ve_x + \PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\ve_y=\goverbrace{\left(\ve_x\PD{}{\xcol{x}} + \ve_y\PD{}{\ycol{y}}\right)}^{演算子}\goverbrace{f\kakko{\xcol{x},\ycol{y}}}^{関数} \end{equation} のように分解し、演算子の部分に名前をつける演算子$\ve_x\PD{}{\xcol{x}} + \ve_y\PD{}{\ycol{y}}$と書くときは、「何を固定するか」を表す$)_{\!\ycol{y}}$などは省略しているが、「二つの変数のうち一方で偏微分するときはもう片方の変数は固定する」という暗黙の了解である。。
$\opcol{\vec \nabla}$の定義(2次元直交座標)
\begin{equation} \opcol{\vec\nabla} =\ve_x\PD{}{\xcol{x}} + \ve_y\PD{}{\ycol{y}}\label{chokunabla} \end{equation}
この記号$\nabla$は「ナブラ」語源は、このような形をした竪琴の名前。と読む(ベクトル記号は付けない場合も多い)。
$\vgrad{f}$(以下長くなるので$\kakko{\xcol{x},\ycol{y}}$を省略)はこの記号ナブラを使って$\opcol{\vec \nabla} f$と表現することができる。「演算子$\opcol{\vec \nabla}$」を関数$f$に掛けたものが上の式であり、結果はベクトルの値を持っている$\opcol{\vec \nabla}$はこれだけでは値の決まらない式であることに注意。$\sin \theta$が$\sin$と$\theta$に分離できないように、$\opcol{\vec \nabla}f$は$\opcol{\vec \nabla}$と$f$に分離できない(同様に、$\vgrad{f}$は$\opcol{\rm grad}$と$f$には分離できない)。。
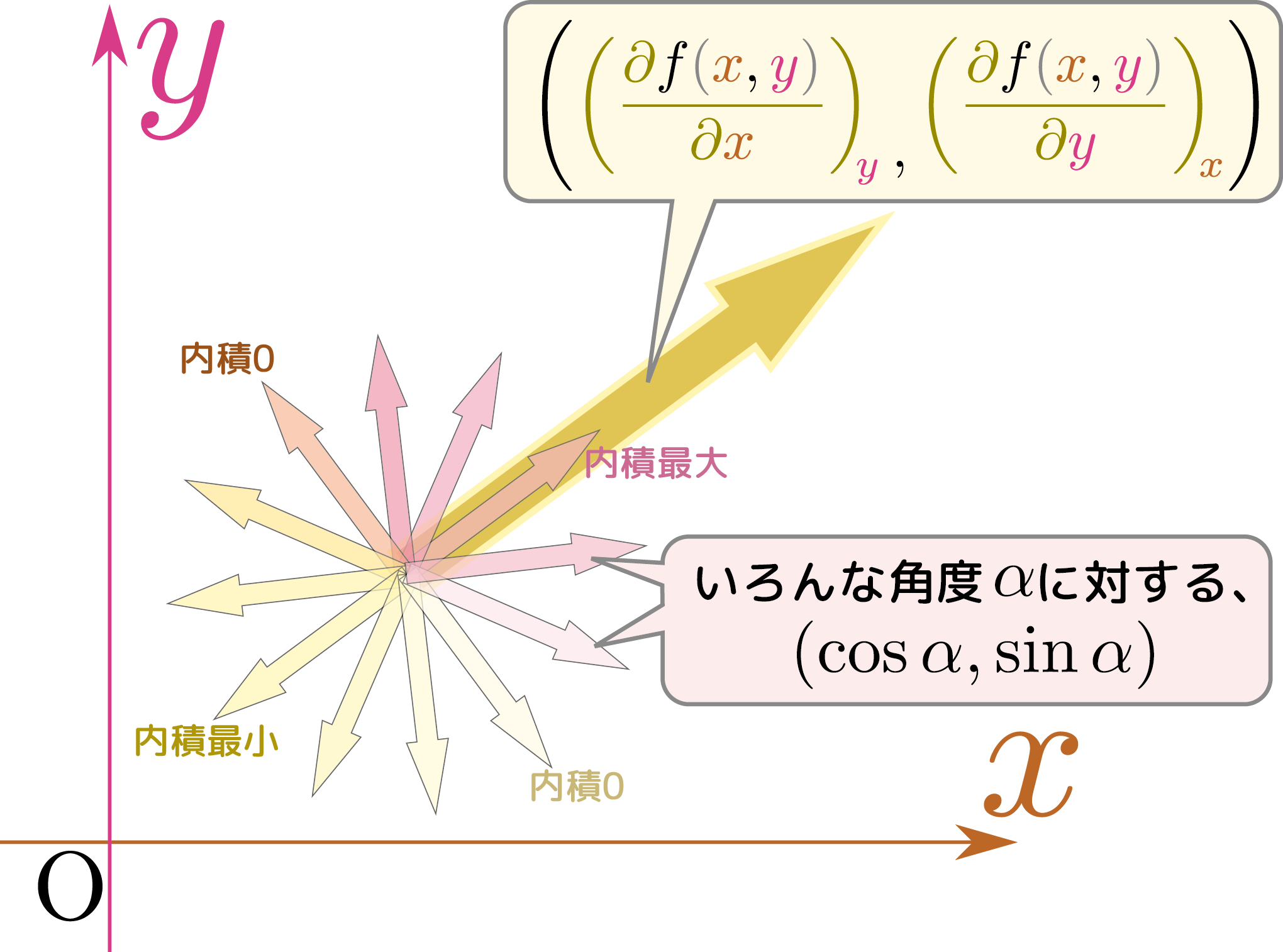
$\vgrad{f}$と欲しい方向の単位ベクトルとの内積を取ることによって、全ての方向の偏微分係数がわかるこれは、全微分が全変数の変化を考えたもので、係数を取り出すことで各方向の偏微分を取り出せたのと同様である。。つまり$\vgrad{f}$はすべての方向の偏微分の情報を含んだベクトル量である。
方向微分の大きさである$\vgrad{f}\cdot\ve_\alpha$は$\alpha$の変化により \begin{equation} -\left| \vgrad{f} \right| \leq \vgrad{f}\cdot\ve_\alpha \leq \left| \vgrad{f} \right| \end{equation} の範囲で変化する内積$\vec a\cdot\vec b$の値は$-|\vec a||\vec b|\leq\vec a\cdot\vec b\leq |\vec a||\vec b|$の範囲であり、今の場合の$\vec b$にあたる$\left(\cos \alpha,\sin \alpha\right)$の長さは1である。。
下の図のような二つの特別な場合を考えよう。

方向微分が0になる場合の$\left(\cos \alpha,\sin \alpha\right)$と、方向微分が最大となる場合の$\left(\cos \alpha,\sin \alpha\right)$は直交している。すなわち、山の斜面に立ったとき「傾きがない方向(等高線に沿って移動する方向)」と「傾きが最大の方向(山を登る方向)」は常に直交している。
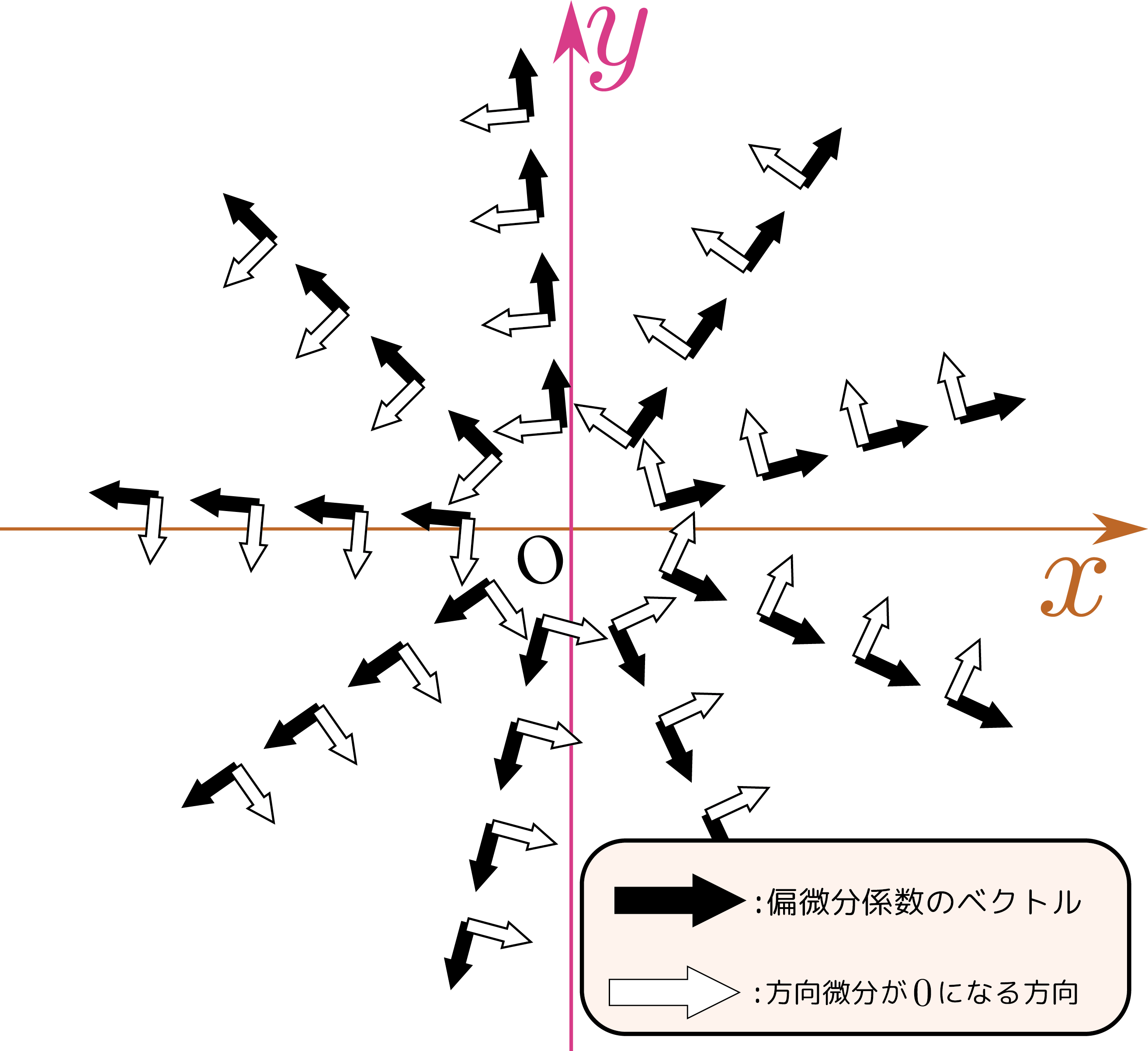
たとえば前に考えた$f\kakko{\xcol{x},\ycol{y}}=\sqrt{\xcol{x}^2+\ycol{y}^2}$という関数の場合、偏微分係数の作るベクトル$\vgrad{f\kakko{\xcol{x},\ycol{y}}}$は \begin{equation} \begin{array}{rl} \left(\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}},\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \right) =\left( {\xcol{x}\over\sqrt{\xcol{x}^2+\ycol{y}^2} } , {\ycol{y}\over\sqrt{\xcol{x}^2+\ycol{y}^2} } \right) \end{array} \end{equation} である。図の黒矢印がこの偏微分係数のベクトル(各点ごとに違う方向を向く)でその長さは$\sqrt{\left({\xcol{x}\over\sqrt{\xcol{x}^2+\ycol{y}^2} } \right)^2+\left({\ycol{y}\over\sqrt{\xcol{x}^2+\ycol{y}^2} } \right)^2 }=1$になる。
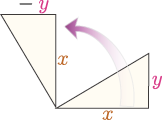
これに垂直なベクトルを白矢印で示した。平面上の90°$\left({\pi\over 2}{\rm rad}\right)$回転は\二段{$\xcol{x}$成分を$\ycol{y}$成分に}{$\ycol{y}$成分$\times(-1)$を$\xcol{x}$成分に}すればよいから、白矢印のベクトルは \begin{equation} \left(-\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}},\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} \right)= \left( {-\ycol{y}\over\sqrt{\xcol{x}^2+\ycol{y}^2} } , {\xcol{x}\over\sqrt{\xcol{x}^2+\ycol{y}^2} } \right) \end{equation} である$\xcol{x}$成分は$\ycol{y}$微分$\times(-1)$、$\ycol{y}$成分は$\xcol{x}$微分というベクトル$-\PD{f}{\ycol{y}}\ve_x+\PD{f}{\xcol{x}}\ve_y$が「$f\kakko{\xcol{x},\ycol{y}}$を一定にする方向を表す」と認識しておくといつか役立つかもしれない。たとえば解析力学の正準方程式の右辺は$\xcol{x}\to p$(運動量)、$\ycol{y}\to q$(座標)と置き換えるとこの形になっていて、$f$にあたるものが保存する式になっている。。このベクトルは「$\sqrt{\xcol{x}^2+\ycol{y}^2}$の微分が0になる方向」すなわち「$\sqrt{\xcol{x}^2+\ycol{y}^2}$が変化しない方向」を向く($\sqrt{\xcol{x}^2+\ycol{y}^2}$が原点からの距離であることを思えば自明)。
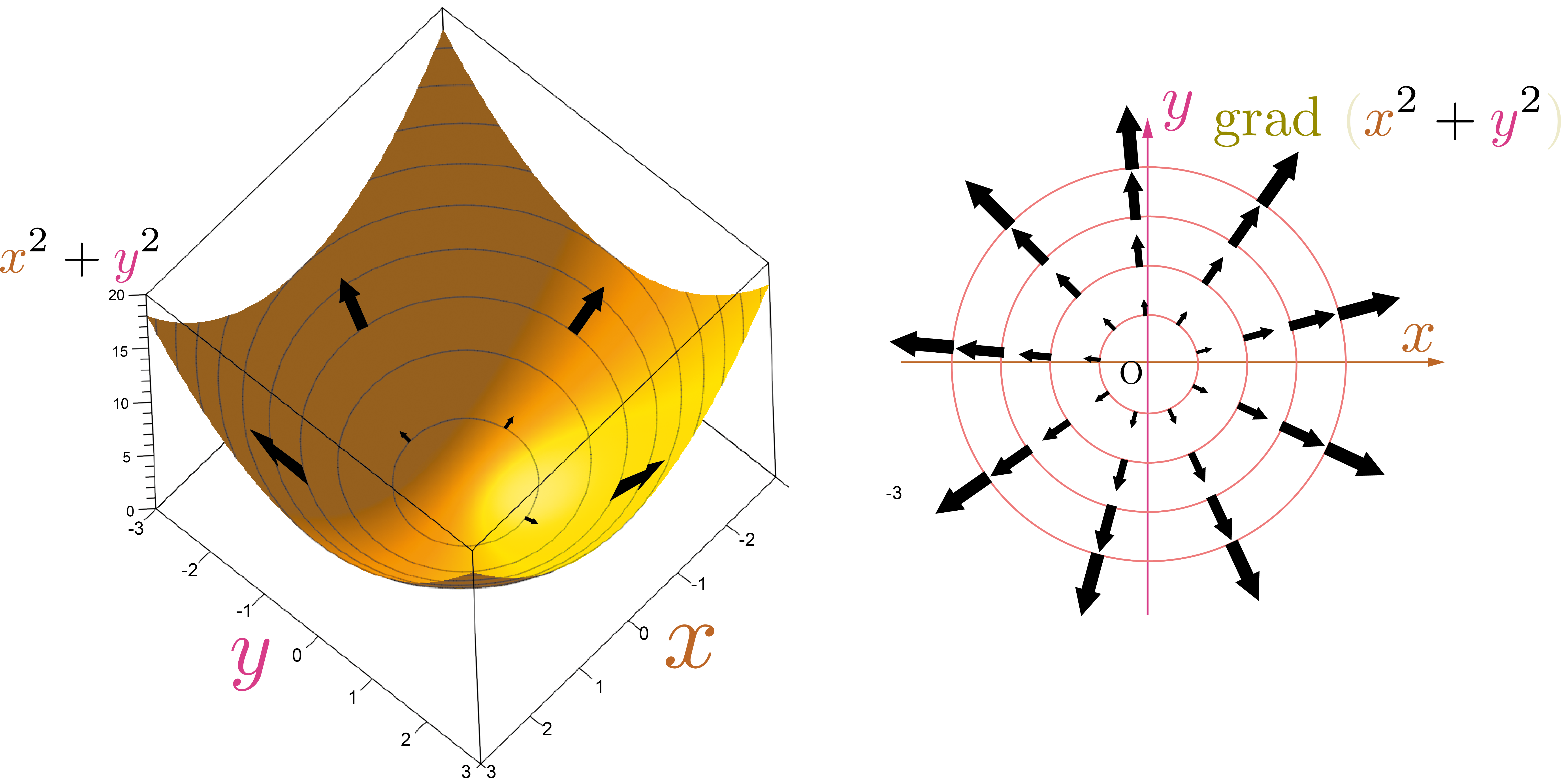
上の図は2変数関数$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}^2+\ycol{y}^2$の立体グラフとその偏微分係数のベクトルの図である。立体グラフの方を見ると、この偏微分係数のベクトル($\vgrad{f}$)は「山を登る方向」を示しており、その長さは「坂の傾斜」を表していることが見てとれる。
$f\kakko{\xcol{x},\ycol{y}}=\sqrt{\xcol{x}^2+\ycol{y}^2}$の場合との違いは、ベクトルの長さである。この場合、 \begin{equation} \begin{array}{rl} & \left(\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}},\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \right) =\left(2\xcol{x}, 2\ycol{y} \right) \end{array} \end{equation} となるから、ベクトルの長さ$\sqrt{(2\xcol{x})^2+(2\ycol{y})^2}$は原点から離れるにしたがって長くなる。
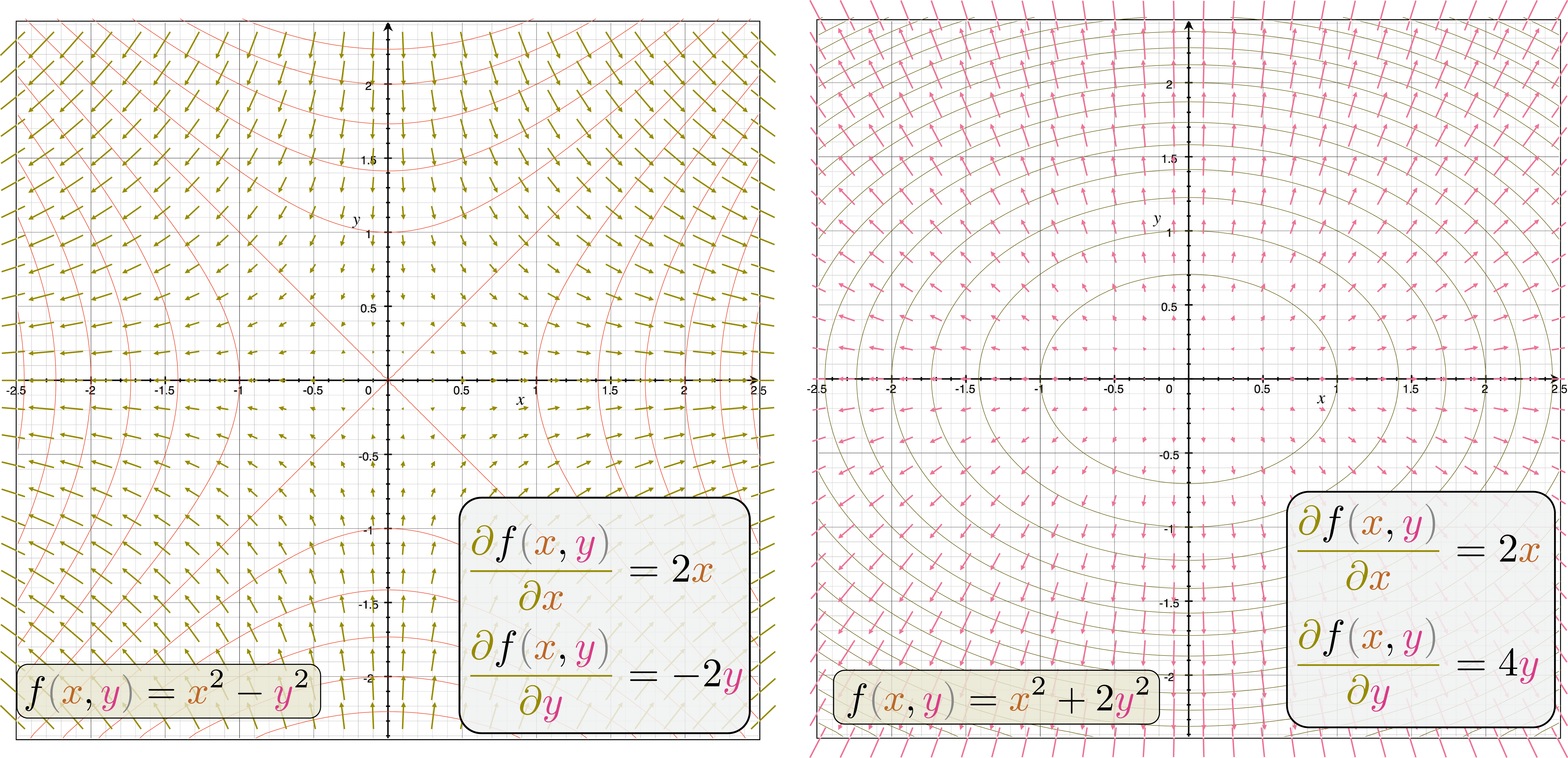
上の図は、$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}^2-\ycol{y}^2$と$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}^2+2\ycol{y}^2$の場合の等高線($f\kakko{\xcol{x},\ycol{y}}=1,2,3,\ldots$となる点を示している)と、偏微分係数($\vgrad{f}$)のベクトルを矢印で表現して描いたものである。
- $\vgrad{f}$と等高線が垂直であること
- 等高線の間隔が狭いところでは、$\vgrad{f}$が長い(微係数が大きい)こと
などを確認しよう。
平面座標と偏微分
座標変換による偏微分の変換
$\ve_r=\cos \thetacol{\theta}\ve_x+\sin \thetacol{\theta}\ve_y$であり、直交する$\ve_\theta$は$\ve_\theta=-\sin \thetacol{\theta}\ve_x+\cos \thetacol{\theta}\ve_y$である。よって、$\rcol{r}$方向と$\thetacol{\theta}$方向の方向微分はそれぞれ \begin{equation} \ve_r\cdot(\vgrad{f})= \cos \thetacol{\theta}\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}+\sin \thetacol{\theta}\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}\label{rhoukou} \end{equation} \begin{equation} \ve_\theta\cdot(\vgrad{f})= -\sin \thetacol{\theta}\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}+\cos \thetacol{\theta}\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}\label{thetahoukou} \end{equation} となる。上の式は$f\kakko{\xcol{x},\ycol{y}}$の$\rcol{r}$微分に一致するが、下の式の方は$f\kakko{\xcol{x},\ycol{y}}$の$\thetacol{\theta}$微分と一致しない。そのことを以下で確認するには$\xcol{x},\ycol{y}$による微分と$\rcol{r},\thetacol{\theta}$による微分の間の関係式が欲しい。そこで、直交座標で考えた関数$f\kakko{\xcol{x},\ycol{y}}$を、極座標で書き直すところから始めよう。直交座標の関数を極座標での関数に書き直した結果を関数$g\,\kakko{\rcol{r},\thetacol{\theta}}$として関数の名前を変えずにこちらも$f\kakko{\rcol{r},\thetacol{\theta}}$と書く流儀もあるが、その場合は関数の形が変わっていることに注意。、 \begin{equation} f\kakko{\xcol{x},\ycol{y}}\biggr|_{\xcol{x}=\rcol{r}\cos \thetacol{\theta},\atop\ycol{y}=\rcol{r}\sin \thetacol{\theta}\phantom{,}}=g\,\kakko{\rcol{r},\thetacol{\theta}} \end{equation} と書こう。一例を示すなら、$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}\ycol{y}$とすれば、$g\,\kakko{\rcol{r},\thetacol{\theta}}=\rcol{r}^2\cos\thetacol{\theta}\sin\thetacol{\theta}$である。これを、 \begin{equation} f\kakko{ {x}\,\kakko{\rcol{r},\thetacol{\theta}},{y}\,\kakko{\rcol{r},\thetacol{\theta}}} =g\,\kakko{\rcol{r},\thetacol{\theta}}\label{fxyrtheta} \end{equation} と表現してもよい。$\rcol{r},\thetacol{\theta}$を決めると${x}\,\kakko{\rcol{r},\thetacol{\theta}}$と${y}\,\kakko{\rcol{r},\thetacol{\theta}}$が決まり、それにより$f$の値が決まる。$f\kakko{x\,\kakko{\rcol{r},\thetacol{\theta}},y\,\kakko{\rcol{r},\thetacol{\theta}}}$を($\thetacol{\theta}$を一定として)$\rcol{r}$で微分する。偏微分の連鎖律を使うと以下の式が出る。 \begin{equation} \PD{f\kakko{x\,\kakko{\rcol{r},\thetacol{\theta}},y\,\kakko{\rcol{r},\thetacol{\theta}}}}{\rcol{r}} =\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}\PD{x\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}} +\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}\PD{y\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}\label{delfdelrkekka} \end{equation}
同様に、${\thetacol{\theta}}$の方の微分は以下の通り。 \begin{equation} \PD{f\kakko{x\,\kakko{\rcol{r},\thetacol{\theta}},y\,\kakko{\rcol{r},\thetacol{\theta}}}}{{\thetacol{\theta}}} =\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}\PD{x\,\kakko{\rcol{r},\thetacol{\theta}}}{{\thetacol{\theta}}} +\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}\PD{y\,\kakko{\rcol{r},\thetacol{\theta}}}{{\thetacol{\theta}}}\label{delfdelthetakekka} \end{equation}
行列をすでに知っている人は、上の二つの式をまとめて、 \begin{equation} \left(\begin{array}{c} \PD{f\kakko{x\,\kakko{\rcol{r},\thetacol{\theta}},y\,\kakko{\rcol{r},\thetacol{\theta}}}}{\rcol{r}}\\[3mm] \PD{f\kakko{x\,\kakko{\rcol{r},\thetacol{\theta}},y\,\kakko{\rcol{r},\thetacol{\theta}}}}{{\thetacol{\theta}}} \end{array}\right)= \left( \begin{array}{cc} \PD{x\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}} & \PD{y\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}\\[3mm] \PD{x\,\kakko{\rcol{r},\thetacol{\theta}}}{{\thetacol{\theta}}} & \PD{y\,\kakko{\rcol{r},\thetacol{\theta}}}{{\thetacol{\theta}}} \end{array}\right) \left(\begin{array}{c} \PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}} \\[3mm] \PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}} \end{array}\right) \end{equation} と書けることを知っておくとよい。線形代数はいろんなところで役に立つが、多変数関数の変数変換でも計算の見通しをよくしてくれる。
ここで、$x\,\kakko{\rcol{r},\thetacol{\theta}}=\rcol{r}\cos \thetacol{\theta},y\,\kakko{\rcol{r},\thetacol{\theta}}=\rcol{r}\sin \thetacol{\theta}$であることから、 \begin{equation} \PD{x\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}=\cos\thetacol{\theta},~~ \PD{y\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}=\sin\thetacol{\theta}\label{delxdelr} \end{equation} である。それを図で表現しよう(次の図参照)。
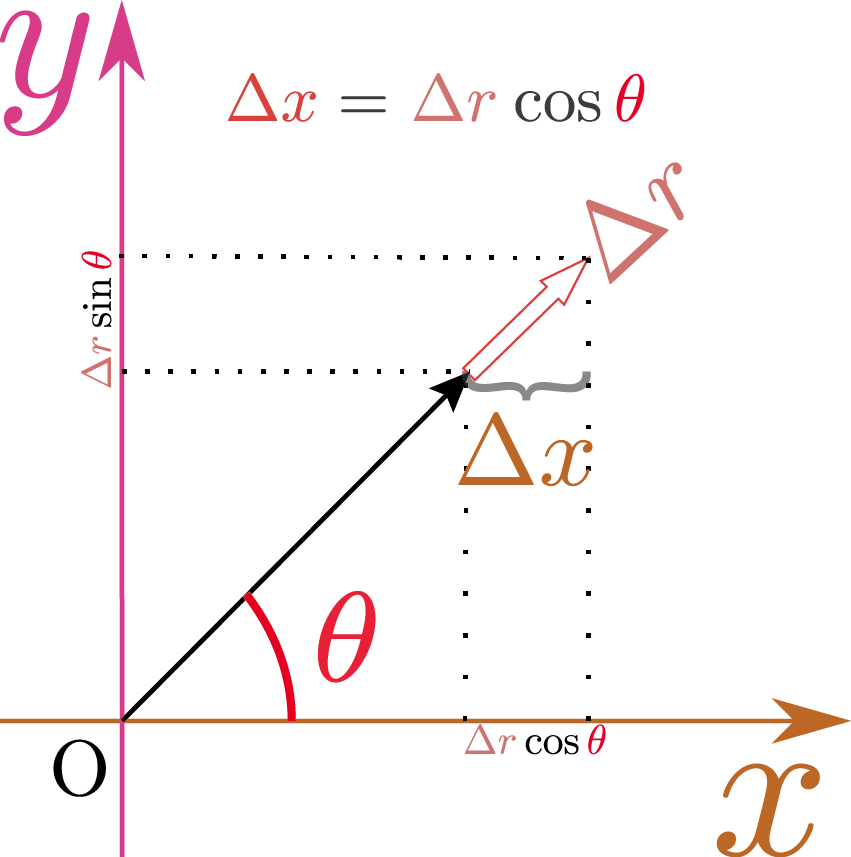
$\PD{x}{\rcol{r}}$という量は、$\thetacol{\theta}$が変化せずに$\rcol{r}$が$\rcol{\Delta r}$だけ変化したときの${\xcol{x}の変化\over \rcol{r}の変化}$であるから、$\PD{x\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}=\cos\thetacol{\theta}$が出てくる。
同様に$\PD{y\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}=\sin\thetacol{\theta}$なので、 \begin{equation} \PD{f\kakko{x\,\kakko{\rcol{r},\thetacol{\theta}},y\,\kakko{\rcol{r},\thetacol{\theta}}}}{\rcol{r}} =\gunderbrace{\cos\thetacol{\theta}}_{\PD{x\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}}\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}} +\gunderbrace{\sin\thetacol{\theta}}_{\PD{y\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}}\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}} \end{equation} と書き直され、確かに$\rcol{r}$方向の方向微分である。すなわち \begin{equation} \ve_r\cdot(\vgrad{f\kakko{\xcol{x},\ycol{y}}})= \PDC{f\kakko{x\,\kakko{\rcol{r},\thetacol{\theta}}, y\,\kakko{\rcol{r},\thetacol{\theta}}}}{\rcol{r}}{\thetacol{\theta}} \end{equation} が成り立つ($\vgrad{f}$の$\rcol{r}$方向の成分は$\PD{f}{\rcol{r}}$)。一方、$\thetacol{\theta}$による偏微分は、 \begin{equation} \begin{array}{rl} \PD{f\bigl(x\,\kakko{\rcol{r},\thetacol{\theta}},y\,\kakko{\rcol{r},\thetacol{\theta}} \bigr)}{{\thetacol{\theta}}} =&\goverbrace{-\rcol{r}\sin {\thetacol{\theta}}}^{\PD{x\,\kakko{\rcol{r},\thetacol{\theta}}}{{\thetacol{\theta}}}} ~\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}} +\goverbrace{\rcol{r}\cos {\thetacol{\theta}}}^{\PD{y\,\kakko{\rcol{r},\thetacol{\theta}}}{{\thetacol{\theta}}}}~\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}} \end{array}\label{delthetatheta} \end{equation} となり、$\thetacol{\theta}$方向の方向微分とは、$\rcol{r}$倍違う$\left(\ve_\theta\cdot(\vgrad{f\kakko{x\,\kakko{\rcol{r},\thetacol{\theta}}},y\,\kakko{\rcol{r},\thetacol{\theta}}})={1\over \rcol{r}}\PD{f\kakko{x\,\kakko{\rcol{r},\thetacol{\theta}},y\,\kakko{\rcol{r},\thetacol{\theta}}}}{\thetacol{\theta}}\right)$。
以上をまとめると、$\ve_r\cdot\vgrad{f}=\PD{f}{\rcol{r}},\ve_\theta\cdot\vgrad{f}={1\over \rcol{r}}\PD{f}{\thetacol{\theta}}$となるので、 \begin{equation} \vgrad{f}=\ve_r\PD{f}{\rcol{r}}+\ve_\theta{1\over \rcol{r}}\PD{f}{\thetacol{\theta}} \end{equation} であることがわかる。よって、2次元極座標のナブラは以下のように定義される。
$\opcol{\vec \nabla}$の定義(2次元極座標)
\begin{equation} \opcol{\vec \nabla}=\ve_r\PD{}{\rcol{r}}+{1\over \rcol{r}}\ve_\theta\PD{}{\thetacol{\theta}}\label{kyunabla} \end{equation}微分の変換からも確認できる。 \begin{equation} \begin{array}{rl} \PD{}{\rcol{r}}= \gunderbrace{\PDC{x\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}{\thetacol{\theta}}}_{\cos\thetacol{\theta}} \PD{}{\xcol{x}}+ \gunderbrace{\PDC{y\,\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}{\thetacol{\theta}}}_{\sin\thetacol{\theta}} \PD{}{\ycol{y}},~~~ \PD{}{\thetacol{\theta}}=& \gunderbrace{\PDC{x\,\kakko{\rcol{r},\thetacol{\theta}}}{\thetacol{\theta}}{\rcol{r}}}_{-\rcol{r}\sin\thetacol{\theta}} \PD{}{\xcol{x}}+ \gunderbrace{\PDC{y\,\kakko{\rcol{r},\thetacol{\theta}}}{\thetacol{\theta}}{\rcol{r}}}_{\rcol{r}\cos\thetacol{\theta}} \PD{}{\ycol{y}}\\ \end{array}\label{rthetaxykankei} \end{equation} という微分の変換式を代入すれば、 \begin{equation} \begin{array}{rl} \opcol{\vec \nabla} =&\ve_r\left(\cos\thetacol{\theta}\PD{}{\xcol{x}}+\sin\thetacol{\theta}\PD{}{\ycol{y}}\right) +{1\over \rcol{r}}\ve_\theta\left(-\rcol{r}\sin \thetacol{\theta}\PD{}{\xcol{x}}+\rcol{r}\cos \thetacol{\theta}\PD{}{\ycol{y}}\right)\\[3mm] =&\gunderbrace{\left(\ve_r\cos\thetacol{\theta}-\ve_\theta\sin \thetacol{\theta}\right)}_{\ve_x}\PD{}{\xcol{x}} +\gunderbrace{\left(\ve_r\sin\thetacol{\theta}+\ve_\theta\cos \thetacol{\theta}\right)}_{\ve_y}\PD{}{\ycol{y}} \end{array} \end{equation} となって、確かに二つの表現は同じである。
2次元の微小変位ベクトル
直交座標と極座標の微小変位
位置ベクトル$\goverbrace{\colvecx=\xcol{x}\ve_x +\ycol{y}\ve_y}^{直交座標} =\goverbrace{\rcol{r}\ve_r}^{極座標}$の全微分を計算すると「微小変位ベクトル」が計算できる。微小変位ベクトルは直交座標でも極座標でも同じベクトルなのだが、表現は異なる。
直交座標の方では、変化するのは(変数なのは)$\xcol{x},\ycol{y}$のみで$\ve_x,\ve_y$は場所に依らない($\diff \ve_x=0,\diff\ve_y=0$)ので、 \begin{equation} \coldvecx = \coldx \ve_x +\coldy \ve_y\label{dvecxxy} \end{equation} となる(記号$\coldvecx$は$\colvecx$の微小変化を表現している)。
直交座標の場合は比較的単純に微小変化を計算できる一方、極座標の場合は$\ve_r$と$\ve_\theta$が場所によって変化する(前にも述べたように、厳密には$\ve_r\kakko{\thetacol{\theta}},\ve_\theta\kakko{\thetacol{\theta}}$と書くべき)ため、注意が必要である。
$\ve_r$の全微分は \begin{equation} \diff \ve_r = \coldtheta \ve_\theta\label{nijigeneretheta} \end{equation} となる。
これは二つの方法で計算できる。
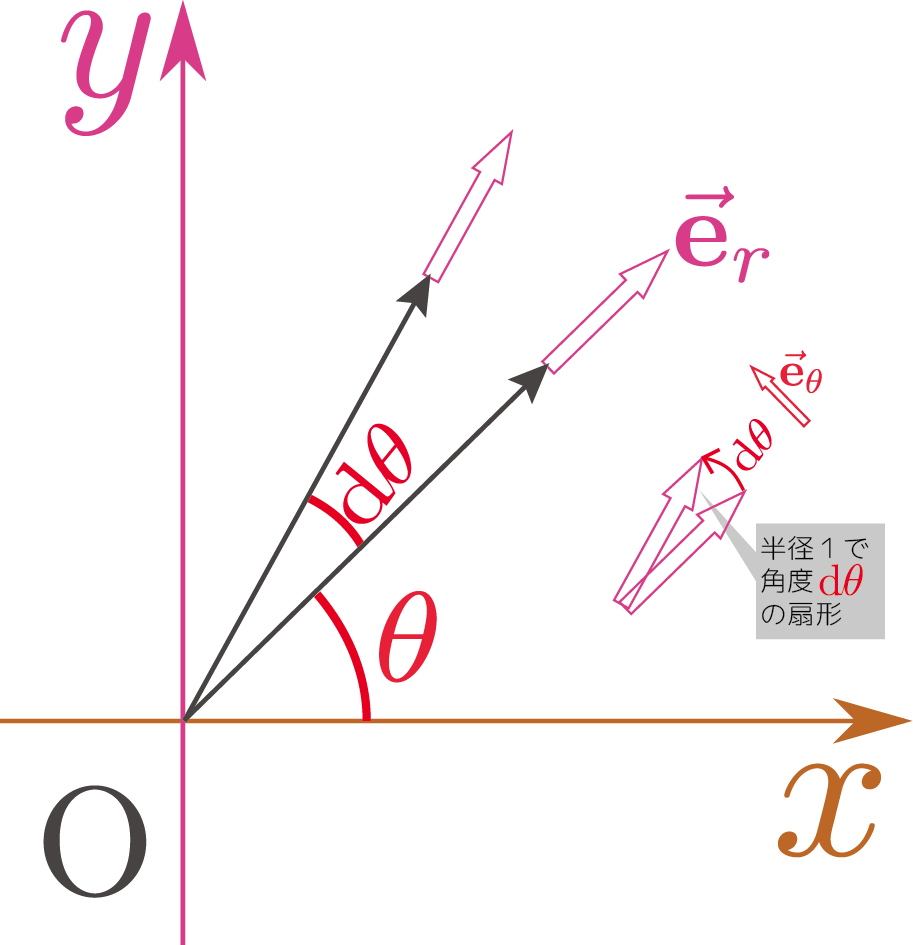
$\thetacol{\theta}$が$\coldtheta$だけ違う場所の$\ve_r$は、角度$\coldtheta$だけ違う方向を向いている。$\ve_r$は長さ1である。長さが1で角度が$\coldtheta$違う二つの差を取ると、結果は長さ$\coldtheta$のベクトルとなり、その方向は$\ve_\theta$と同じ方向を向いている(図にあるように、二つの$\ve_r$は半径1で中心角$\coldtheta$の扇形を作り、弧の長さが$\coldtheta$)と考えると$\diff \ve_r = \coldtheta \ve_\theta$がわかる。
$\ve_r=\cos \thetacol{\theta}\ve_x+\sin\thetacol{\theta}\ve_y$の全微分を計算することでもこれはわかる。 \begin{equation} \begin{array}{rl} \diff \left(\cos \thetacol{\theta}\ve_x+\sin\thetacol{\theta}\ve_y\right) =&-\sin \thetacol{\theta}\coldtheta\ve_x+\cos \thetacol{\theta}\coldtheta\ve_y\\ =&\left(-\sin \thetacol{\theta}\ve_x+\cos \thetacol{\theta}\ve_y\right)\coldtheta\\ \end{array} \end{equation} となり($\ve_x,\ve_y$の微分は0)、$-\sin \thetacol{\theta}\ve_x+\cos \thetacol{\theta}\ve_y=\ve_\theta$なので、上の式が導かれる。
よって、極座標での微小変位のベクトルは \begin{equation} \coldvecx = \coldr\ve_r+\rcol{r}\coldtheta\ve_\theta\label{coldvecxrtheta} \end{equation} のように表せる。$\rcol{r}\ve_r$という「数とベクトルの積」に対してもライプニッツ則を使って計算してよいので、ここでは$\diff \left(\rcol{r}\ve_r\right)=\coldr\ve_r+\rcol{r}\diff\ve_r$のように微分を行った。 となる。もちろんこれらの式は$\xcol{x}=\rcol{r}\cos\thetacol{\theta}$などを微分することによっても得られるが、ベクトルの内積を使っても同じ計算ができるわけである。これらの式は、まとめて \begin{equation} \left(\begin{array}{cc}{\coldx\\\coldy}\end{array}\right) =\left(\begin{array}{cc} \cos \thetacol{\theta}~~&-\rcol{r}\sin\thetacol{\theta}\\ \sin \thetacol{\theta}~~&\rcol{r}\cos\thetacol{\theta}\\ \end{array}\right)\left(\begin{array}{cc}\coldr\\ \coldtheta\end{array}\right),~~~~~ \left(\begin{array}{c}\coldr\\ \coldtheta\end{array}\right) =\left(\begin{array}{cc} \cos \thetacol{\theta}~~&\sin\thetacol{\theta}\\ -{\sin \thetacol{\theta}\over \rcol{r}}~~&{\cos\thetacol{\theta}\over \rcol{r}}\\ \end{array}\right) \left(\begin{array}{cc}\coldx\\\coldy\end{array}\right) \end{equation} のように行列で表示することもできる。上の二つの行列は互いに逆行列である。
極座標での微小変位ベクトルは上で述べたように$\coldvecx=\coldr\ve_r+\rcol{r}\coldtheta\ve_\theta$なのであるが、これは極座標のナブラの式$\opcol{\vec \nabla}=\ve_r\PD{}{\rcol{r}}+{1\over \rcol{r}}\ve_\theta\PD{}{\thetacol{\theta}}$と、(微小変位は$\thetacol{\theta}$成分に$\rcol{r}$が掛かり、$\opcol{\vec \nabla}$は$\thetacol{\theta}$成分が$\rcol{r}$で割られているという意味で)「対」になっていることに気づくだろう。
座標系に依らない$\opcol{\vec \nabla}$の定義からもその意味がわかる。極座標での微小変化の様子は \begin{equation} \begin{array}{rl} f\kakko{\rcol{r}+\coldr,\thetacol{\theta}+\coldtheta} =&f\kakko{\rcol{r},\thetacol{\theta}} +\coldr\PD{f\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}} +\coldtheta\PD{f\kakko{\rcol{r},\thetacol{\theta}}}{\thetacol{\theta}} \end{array}\label{kyokunabladasu} \end{equation} である。極座標では$\coldvecx=\coldr\ve_r+\rcol{r}\coldtheta\ve_\theta$であることを考えると、第2項と第3項は、$\coldr\PD{f\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}+\rcol{r}\coldtheta\times{1\over \rcol{r}}\PD{f\kakko{\rcol{r},\thetacol{\theta}}}{\thetacol{\theta}}$のように書き直すことで$\coldvecx \cdot \opcol{\vec \nabla} f$の形になる。「$\coldvecx$の中の$\coldtheta$の前に$\rcol{r}$がついて掛けられていたため、$\coldvecx$と内積を取る相手である$\opcol{\vec \nabla}$の中の$\PD{}{\thetacol{\theta}}$の方に${1\over \rcol{r}}$を掛けなくてはいけない」と考えると、$\thetacol{\theta}$微分の前の係数の意味が理解できる。