線積分
2次元の線上の積分
多変数関数のいろいろな積分を考えることにする。以下ではまず2次元面上の積分を考えよう。
2次元面の線上でスカラー関数を積分する
まずは2変数関数$f\kakko{\xcol{x},\ycol{y}}$を積分することを考える。後で「ベクトルの値を持つ関数」の積分を考えるが、まずここでは2変数関数$f\kakko{\xcol{x},\ycol{y}}$（位置座標を決めるとある値が決まるという関数）を考える。そこでこの関数を「スカラー関数」「スカラー」「ベクトル」という言葉には使用する分野や文脈に応じていろんな意味があるのだが、ここでは「向きのある量がベクトル、向きのない量がスカラー」あるいは「1成分しかない量がスカラー、$\xcol{x}$成分、$\ycol{y}$成分を持つ量がベクトル」である。と呼んでおくことにする。
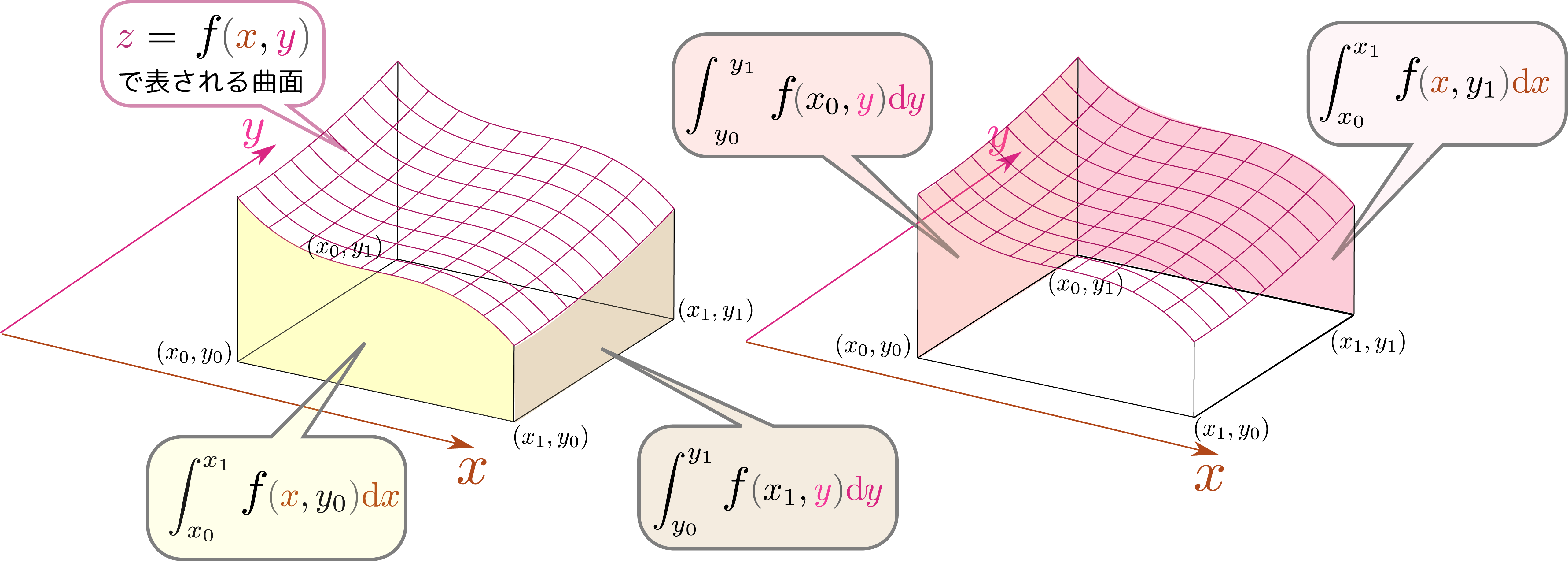
次の図は二つの積分を「上から見た」ものである。
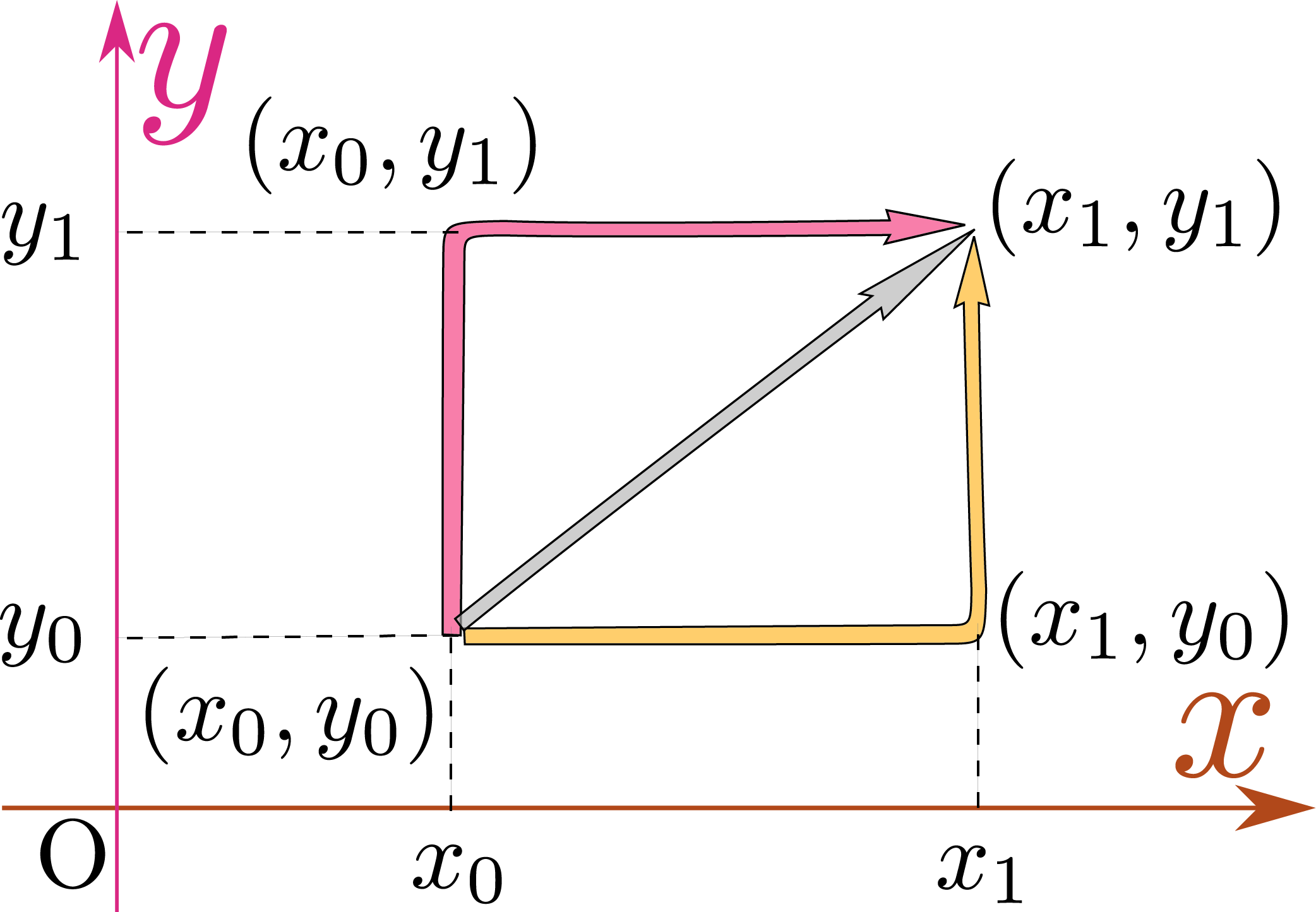
という経路に沿った積分は、どちらも$(x_0,y_0)$から$(x_1,y_1)$までの積分である。要は北東にある自宅に帰るのに、「東に行ってから北へ行くか、北に行ってから東に行くか」という選択肢がある。この二つの積分結果は運が良くない限り一致しない。
二つの積分を式で表すと
$\int_{x_0}^{x_1}f\kakko{\xcol{x},y_0}\coldx$
と
$\int_{y_0}^{y_1}f\kakko{x_0,\ycol{y}}\coldy+ \int_{x_0}^{x_1}f\kakko{\xcol{x},y_1}\coldx$
である（図を見ながら確認しよう）。
経路の選択肢は他にもある。たとえば、
のような斜めに直進する積分もしたくなるところである。もちろんもっと一般的には、曲線も有り得る。積分を行うには今考えている関数の値 $\times$ 微小長さを考えてこれを「足算」していけばいい。斜め線の場合の微小長さは$\sqrt{\coldx^2+\coldy^2}$になることを考えて積分を行う。具体的には$\sqrt{\coldx^2+\coldy^2}=\sqrt{1+\left({\coldy\over\coldx}\right)^2}\coldx$となることを使って、考えている曲線上で$\ycol{y}=g\,\kakko{\xcol{x}}$という式が成り立っているならば
\begin{equation}
\int_{x_0}^{x_1}f\kakko{\xcol{x},\ycol{y}}\sqrt{1+\left({\coldy\over\coldx}\right)^2}\coldx
= \int_{x_0}^{x_1}f\kakko{\xcol{x},g\,\kakko{\xcol{x}}}\sqrt{1+\left(g'\kakko{\xcol{x}}\right)^2}\coldx
\end{equation}
という積分を行えば、$\int$今考えている関数の値$\times$微小長さが計算できたことになる。
線の長さ
$f\kakko{\xcol{x},\ycol{y}}=1$であるような特別な場合、上の積分は$\sqrt{\left({\coldx\over \coldtau}\right)^2+\left({\coldy\over\coldtau}\right)^2}\coldtau$という微小部分の線の長さを足していったもの、つまりは「線の長さ」そのものになる。もっとも単純な例では
\begin{equation}
\int_{x_0}^{x_1}\coldx+ \int_{y_0}^{y_1}\coldy=x_1-x_0+y_1-y_0
\end{equation}
である（これは線の長さ）。斜め線であれば、
\begin{equation}
\int_{x_0}^{x_1}\sqrt{1+\left({\coldy\over\coldx}\right)^2}\coldx
~~または~~ \int_{y_0}^{y_1}\sqrt{\left({\coldx\over\coldy}\right)^2+1}\coldy
\end{equation}
となるが、考えている斜め線においては${\coldy\over \coldx}={y_1-y_0\over x_1-x_0}$であるから、
\begin{equation}
\int_{x_0}^{x_1}\sqrt{1+\left({y_1-y_0\over x_1-x_0}\right)^2}\coldx
= (x_1-x_0)\sqrt{1+\left({y_1-y_0\over x_1-x_0}\right)^2}
= \sqrt{\left(x_1-x_0\right)^2+\left(y_1-y_0\right)^2}
\end{equation}
となる。結果は予想通りである。
次に曲線を考えよう。方程式$\xcol{x}^2+\ycol{y}^2=R^2$で表される円の場合、この式を微分して得られる$\xcol{x}\coldx+\ycol{y}\coldy=0$から${\coldy\over \coldx}=-{\xcol{x}\over \ycol{y}}$となるので、$ \int_{x_0}^{x_1}\sqrt{1+\left({\coldy\over\coldx}\right)^2}\coldx$の方の式を使って、 \begin{equation} \int_0^R \sqrt{1+\left({\xcol{x}\over \ycol{y}}\right)^2}\coldx \end{equation} という積分を行うと${1\over4}$円周が計算できる。$\xcol{x}=R\cos\thetacol{\theta}$という置換をして積分を行う（このとき、$\ycol{y}=R\sin\thetacol{\theta}$になる）。
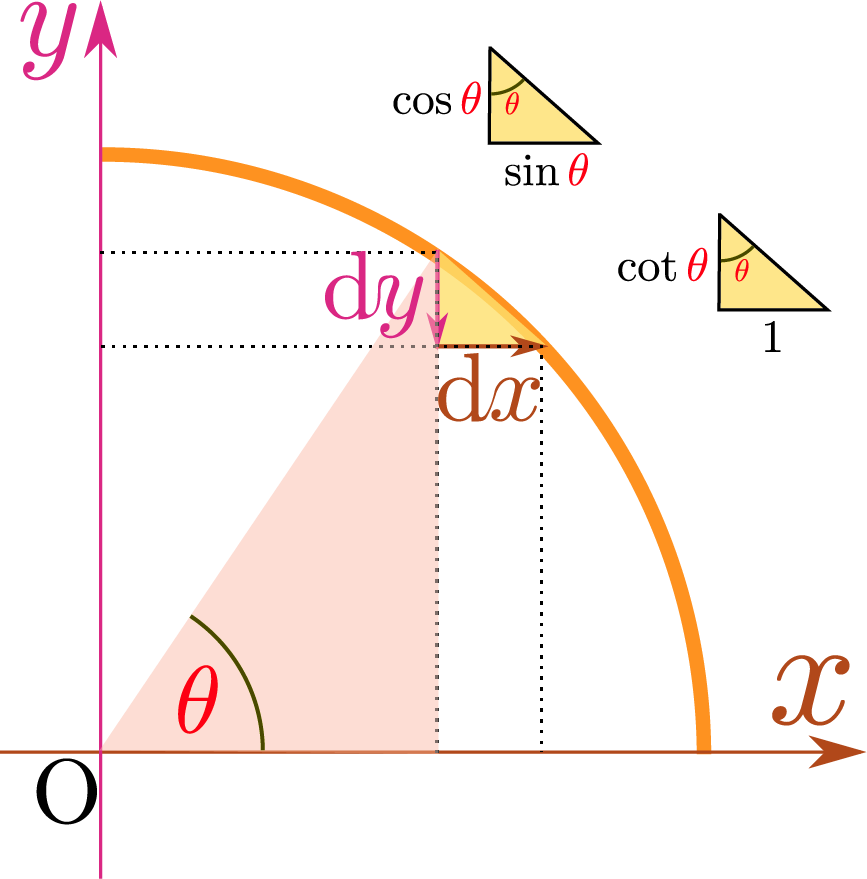
図にも描いたが、この置換を行うと、${\coldy\over \coldx}=-{\xcol{x}\over \ycol{y}}$}は\文中式{$-{\cos\thetacol{\theta}\over \sin\thetacol{\theta}}=-\cot\thetacol{\theta}$}になる。 \begin{equation} \int_{\pi\over 2}^0 \sqrt{1+\left({\cos\thetacol{\theta}\over \sin\thetacol{\theta}}\right)^2}\goverbrace{\left(-R\sin\thetacol{\theta}\coldtheta\right)}^{\coldx} =R\int_0^{\pi\over 2}\coldtheta={\pi R\over 2} \end{equation} となって確かに円周$2\pi R$の${1\over4}$が出る。
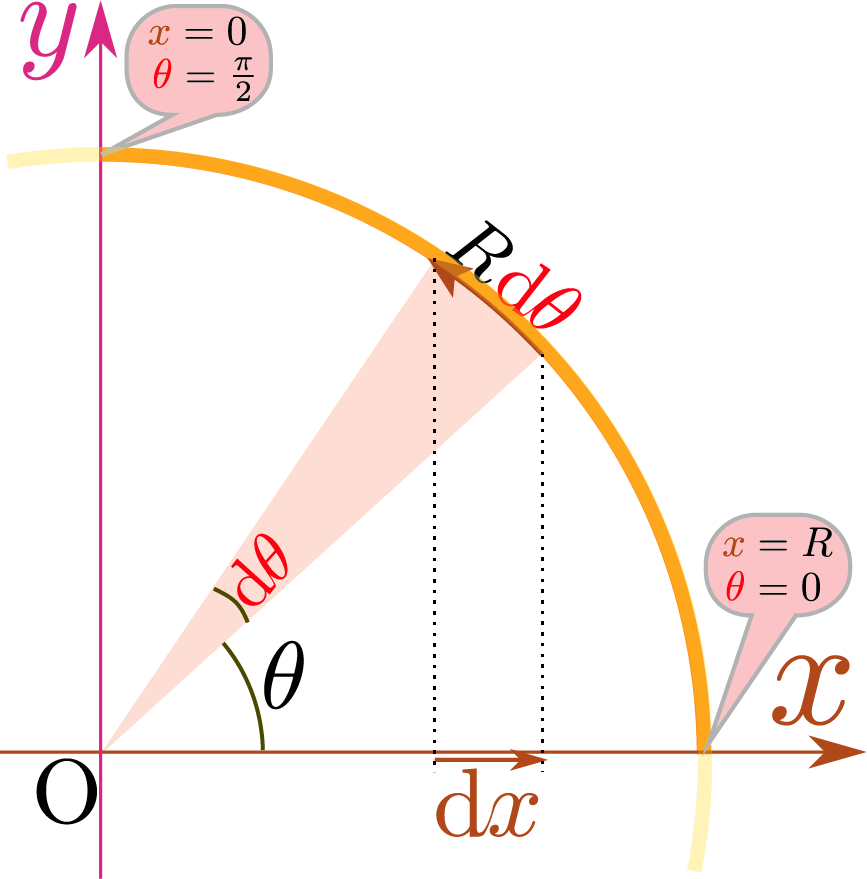
上の計算は、$\xcol{x},\ycol{y}$がともに別のパラメータの関数だとしてもよい。パラメータに$\thetacol{\theta}$を使い\文中式{$\coldx=-R\sin\thetacol{\theta}\coldtheta,\coldy=R\cos\thetacol{\theta}\coldtheta$}と考えて、 \begin{equation} \sqrt{\coldx^2+\coldy^2}=\sqrt{R^2\sin^2\thetacol{\theta}\coldtheta^2+R^2\cos^2\thetacol{\theta}\coldtheta^2} =R\coldtheta \end{equation} のように「微小長さ」を計算してから$\thetacol{\theta}$を$0$から${\pi\over 2}$まで積分してもよい（結果は同じ）。
$\thetacol{\theta}$での積分は右のような\fukidasi{微小長さの和}を計算していることになるから、実は最初から極座標で考えればいっきに$R\int_0^{\pi\over 2}\coldtheta$という（最初から1次元の）積分を行えばよかったことがわかる（半径$R$の円周上の微小な長さは$R\coldtheta$で表現できる）。
ベクトル関数の線積分
ここまでは$f\kakko{\xcol{x},\ycol{y}}$という関数（スカラー関数）があって、それをある線上で積分することを考えた。次に、より応用の多い、ベクトルの値を持つ関数$\vec V\kakko{\xcol{x},\ycol{y}}$（ベクトル関数）を線上で積分する方法について考えよう。
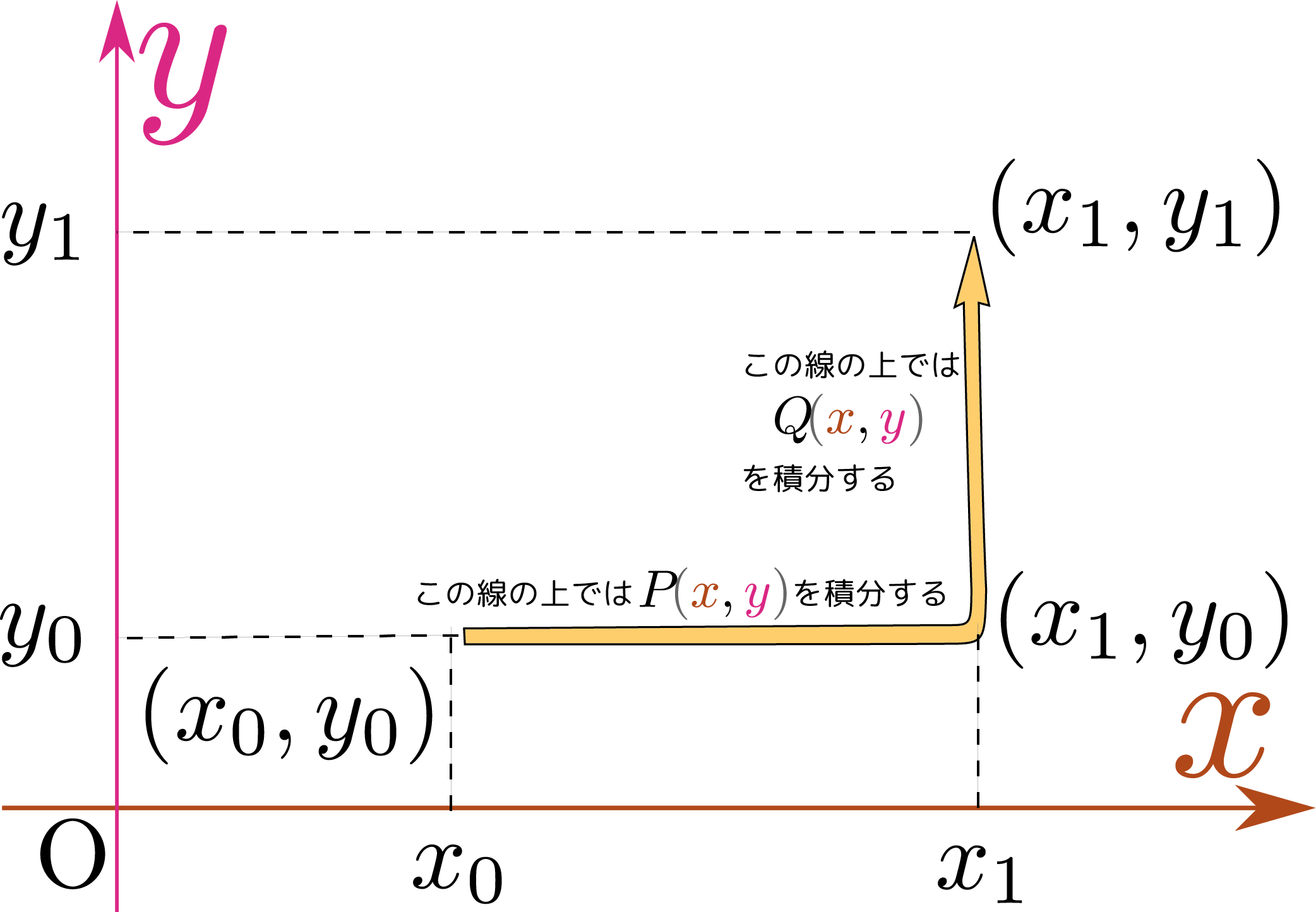
今度は図のように$\xcol{x}$方向の積分をするときと$\ycol{y}$方向で積分するときの被積分関数を変えて、 \begin{equation} \int_{x_0}^{x_1}P\,\kakko{\xcol{x},y_0}\coldx + \int_{y_0}^{y_1}Q\,\kakko{x_1,\ycol{y}}\coldy \end{equation} のような積分を考えることにする。
$P\,\kakko{\xcol{x},\ycol{y}}=A_x\kakko{\xcol{x},\ycol{y}},Q\,\kakko{\xcol{x},\ycol{y}}=A_y\,\kakko{\xcol{x},\ycol{y}}$と書けば、 \begin{equation} \int_{x_0}^{x_1}A_x\kakko{\xcol{x},y_0}\coldx + \int_{y_0}^{y_1}A_y\,\kakko{x_1,\ycol{y}}\coldy \end{equation} となる。積分記号を外した量（被積分関数）である$A_x\coldx+A_y\coldy$はベクトル$\vec A=\left(A_x,A_y\right)$と微小変位ベクトル$\coldvecx=\left(\coldx,\coldy\right)$の内積になっているので、まとめて書くときは$\vec A\cdot\coldvecx$と書く。
こうしてベクトルの値を持つ関数と$\coldvecx$の内積を取ってなんらかの曲線上（ここまで出した例はまだ直線のみであるが）で積分を行った量を「線積分」と呼ぶ。
ここで、2変数の積分はいろんな経路が考えられるという事情があるので「$\int_{\vec x_0}^{\vec x_1}\vec A\kakko{\!\colvecx\!}\cdot \coldvecx$と書いただけでは、どの線に沿って積分するのか、まだ指定されていない」ことに注意しよう。
線積分の応用
仕事と位置エネルギー
ベクトル場の線積分のもっとも重要な応用は、力学における「仕事」の定義であろう。2次元の場合では、以下のように定義される。
物体に力$\vec F$を加えている状態でその物体が$\coldvecx=(\coldx,\coldy)$という微小量だけ動いたとき、この力$\vec F$によってその物体に対して \begin{equation} \vec F\cdot\coldvecx=F_x\coldx+F_y\coldy\goverbrace{+F_z\coldz}^{3次元では\atop これも加える} \end{equation} の仕事がなされたと言う（本来は3次元で定義すべきもので、その場合は$\zcol{z}$成分も足す）。
仕事という量を定義する意味はいろいろあるが、何よりも大事なのは力学における有用な概念である「エネルギー」という物理量が仕事を使うことで定義できることである。エネルギーの定義については後に回して、ここでは仕事のイメージをまず考えよう。
以下では、働く力が場所のみに依る場合を考えることにして、$\vec F$を$\vec F\,\kakko{\!\colvecx\!}$と場所の関数とする。この定義は物体が微小な距離だけ移動した場合であるが、有限区間（$\vec x_0$から$\vec x_1$へ）移動した場合は$\int_{\vec x_0}^{\vec x_1}\vec F\,\kakko{\!\colvecx\!}\cdot\coldvecx$という積分を行う。
微小仕事$\vec F\,\kakko{\!\colvecx\!}\cdot\coldvecx$は場所$\colvecx$において働く力$\vec F\,\kakko{\!\colvecx\!}$と微小変位$\coldvecx$の内積であるが$\vec F$と$\coldvecx$が同じ向き（$\theta=0$）ならば$\vec F\cdot\coldvecx=|\vec F||\coldvecx|$となって大きくなる。
「仕事」の意味を理解するために、風が吹いている中を移動しているところをイメージしよう。風が当たってあなたを押す力を$\vec F$と書くことにする。風が順風（$\vec F$と$\coldvecx$が同じ向き）のときは風があなたを押してくれて、楽に動ける。逆風（$\vec F$と$\coldvecx$が逆向き）のときは風にじゃまされる分だけ動くのがたいへんになる。そこで$\vec F\cdot\coldvecx$という量を「動くときに風のおかげでどれだけ助かるか」という量だと考えることができる（この量がマイナスのときは「負の量だけ助かる＝邪魔される」と考える）。
この場合の仕事$\vec F\cdot\coldvecx$は「風のおかげでどれだけ助けられているか」を表す指標となるわけである。
風の強さと向きは場所によって違うから、$\vec F$は場所の関数\文中式{$\vec F\,\kakko{\!\colvecx\!}=F_x\kakko{\!\colvecx\!}\ve_x+F_y\kakko{\!\colvecx\!}\ve_y$}となり、ある場所$\vec x_0$からある場所$\vec x_1$まで移動したとき、風がしてくれる仕事は \begin{equation} \int_{\vec x_0}^{\vec x_1}\vec F\,\kakko{\!\colvecx\!}\cdot\coldvecx = \int_{\vec x_0}^{\vec x_1}\left(F_x\kakko{\!\colvecx\!}\coldx+F_y\kakko{\!\colvecx\!}\coldy\right) \end{equation} で計算できる。ここで、すでに注意したように$\int_{\vec x_0}^{\vec x_1}$という記号では出発点$\vec x_0$と到着点$\vec x_1$だけが指定されていて経路が指定されていないので計算結果は一通りではない。
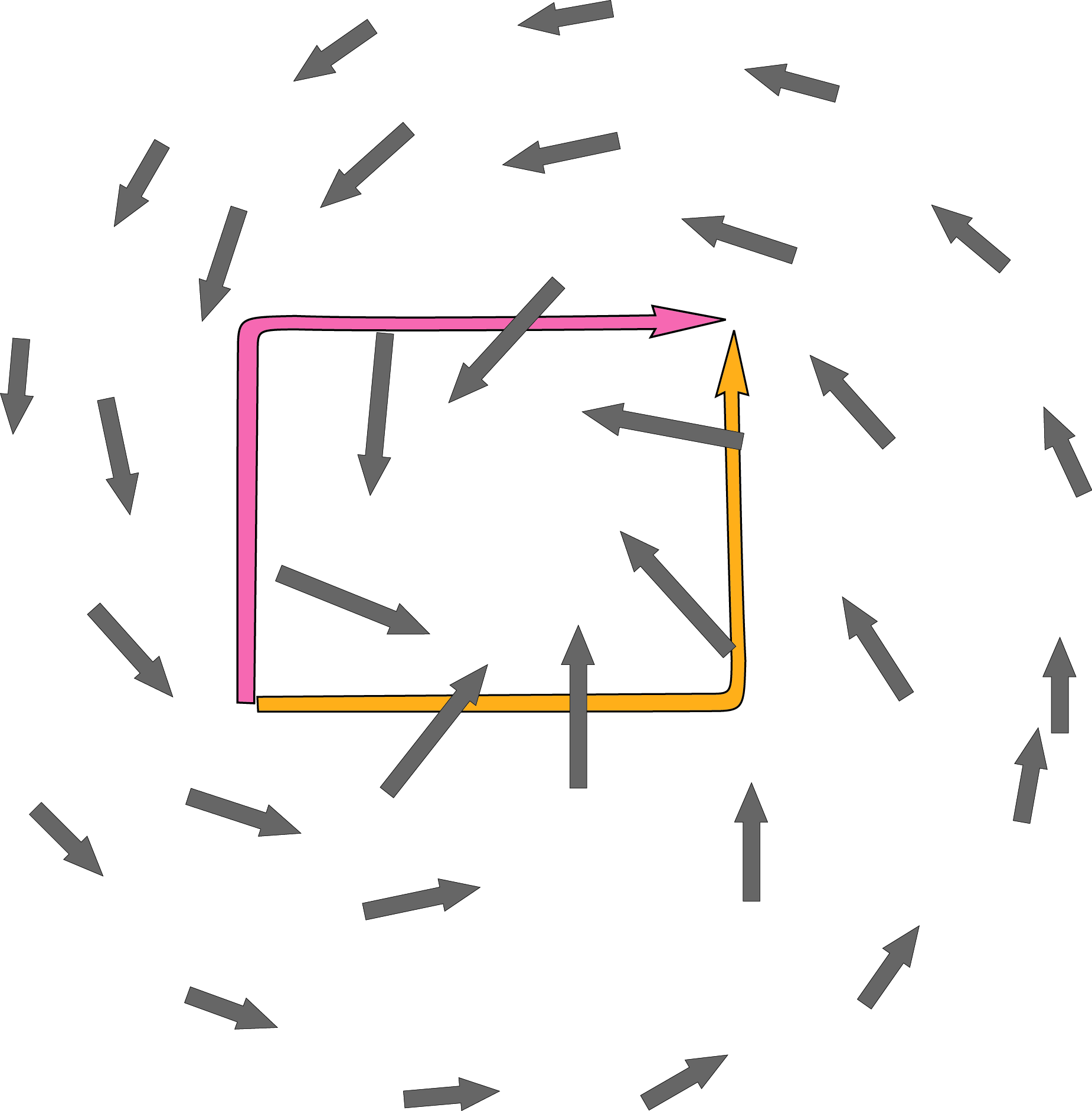
図のように、台風のような風が吹いているとき、のような経路だといかにも「風が押してくれるので楽そう」だし、のような経路だと「逆風で苦労しそう」だ。出発点と到着点が同じでも、「風が助けてくれる」仕事の量が全く違ってくる。
この二つの積分というのは、積分可能条件について考えたときの$U\kakko{\xcol{x},\ycol{y}}=\int_{y_0}^{\ycol{y}} \coldt Q\,\kakko{x_0,\tcol{t}}+\int_{x_0}^{\xcol{x}}\coldt P\,\kakko{\tcol{t},\ycol{y}} $と$U\kakko{\xcol{x},\ycol{y}}=\int_{x_0}^{\xcol{x}}\coldt P\,\kakko{\tcol{t},y_0}+\int_{y_0}^{\ycol{y}} \coldt Q\,\kakko{\xcol{x},\tcol{t}}$という二つの積分と、$P\to F_x,Q\to F_y$と置き換えてみれば同じものである。よって、二つの経路で同じ積分結果を出す、すなわち、 \begin{equation} \int_{y_0}^{\ycol{y}} \coldt F_y\kakko{x_0,\tcol{t}}+ \int_{x_0}^{\xcol{x}}\coldt F_x\kakko{\tcol{t},\ycol{y}} =\int_{x_0}^{\xcol{x}}\coldt F_x\kakko{\tcol{t},y_0}+\int_{y_0}^{\ycol{y}} \coldt F_y\kakko{\xcol{x},\tcol{t}} \end{equation} となるためには、考えている範囲で \begin{equation} \PDC{F_x}{\ycol{y}}{\xcol{x}} - \PDC{F_y}{\xcol{x}}{\ycol{y}}=0 \end{equation} が成り立たなくてはいけない（この式は積分可能条件そのものである）。
$\ycol{y}$軸の負の向きに重力が働いている場合、この力は$\vec F\,\kakko{\!\colvecx\!}=-mg\ve_y$と表される。この場合の場所$(x_0,y_0)$から$(x_1,y_1)$までに移動する間に「重力のする仕事」は \begin{equation} \int_{(x_0,y_0)}^{(x_1,y_1)} \vec F\,\kakko{\!\colvecx\!}\cdot \coldvecx= \int_{(x_0,y_0)}^{(x_1,y_1)} (-mg\ve_y)\cdot({\coldx\ve_x}+\coldy\ve_y)=-mg \int_{y_0}^{y_1} \coldy \end{equation} となり（$\coldx\ve_x$が消えるのは内積$\ve_y\cdot\ve_x=0$による）、実は本質的には1次元の積分になってしまい、結果も簡単に$-mg(y_1-y_0)$となる。つまりこの場合、途中の経路には一切依らずに答は$y_0$と$y_1$だけで決まる。$\vec F\,\kakko{\!\colvecx\!}$が定数ベクトルだから、積分可能条件は満たされている。
そこで、この積分結果（仕事量）が位置エネルギーの差となるように「位置エネルギー」が定義される。すなわち、どこかにエネルギーの基準点$\vec x_0$を設定し、 \begin{equation} U\kakko{\!\colvecx\!}=\gunderbrace{U\kakko{\vec x_0}}_{ここでは0とする}-\int_{\vec x_0}^{\!\colvecx\!}\vec F\,\kakko{\!\colvecx\!}\cdot\coldvecx \end{equation} とすると、積分$\int_{\vec x_0}^{\!\colvecx\!}$がどのような経路で行われているかに依らずに常に同じ値$mg\left(\ycol{y}-y_0\right)$を出すので、矛盾なく$U\kakko{\!\colvecx\!}$が定義できるのである。
1変数の場合と同様に「微分と積分は互いの逆演算」と考えると、$U\kakko{\small\!\colvecx\!}=U\kakko{\vec x_0}-\int_{\vec x_0}^{\!\colvecx\!}\vec F\,\kakko{\!\colvecx\!}\cdot\coldvecx$の逆は$\vec F\,\kakko{\!\colvecx\!}=-\opcol{\vec\nabla}U\kakko{\!\colvecx\!}$となる。このマイナス符号に注意しよう。$\vgrad{f}$は$f$を山の高さだと見たときに「山を登る」方向であったことを思い出そう。力は「位置エネルギーを小さくする方向へ」働くので、登る方向（$\vgrad{f}$の方向）と逆なのである。
重力の例では、 \begin{equation} -\opcol{\vec\nabla}\left(mg\ycol{y}\right) =-\left(\ve_x\PD{}{\xcol{x}}+\ve_y\PD{}{\ycol{y}}\right)(mg\ycol{y}) = -mg \ve_y \end{equation} となる。このマイナス符号は重力が下向きであることを示している。
次に$\vec F\,\kakko{\!\colvecx\!}=-{GMm\over \rcol{r}^2}\ve_r$になる力（万有引力）ほんとうはこの万有引力の式は3次元で成立する式なのだが、ここでは2次元座標のみを考える。の場合を考えよう（こちらでは極座標を使う）。$\coldvecx$も極座標での表現$\coldr\ve_r+\rcol{r}\coldtheta\ve_\theta$を使って表現すれば、内積を取ると$\coldr$に比例する部分のみが残り、$\vec F\,\kakko{\!\colvecx\!}\cdot \coldvecx =-{GMm}\int {1\over \rcol{r}^2}\coldr$となる。これはすぐに \begin{equation} \int \vec F\,\kakko{\!\colvecx\!}\cdot \coldvecx =-{GMm}\int {1\over \rcol{r}^2}\coldr =GMm\left[~~{1\over\rcol{r}}~~\right]^{到着点の\rcol{r}}_{出発点の\rcol{r}} \end{equation} のように積分できて、結果は出発点と到着点の$\rcol{r}$だけに依存する。この計算結果である仕事${GMm\over \rcol{r}}\biggr|_{到着}-{GMm\over \rcol{r}}\biggr|_{出発}$は位置エネルギーの減少分である$U\kakko{出発点}-U\kakko{到着点}$と等しいのだから、この場合の$U\kakko{\!\colvecx\!}$は$-{GMm\over \rcol{r}}$である（符号に注意）。逆にこの$U\kakko{\!\colvecx\!}$から \begin{equation} \vec F\,\kakko{\!\colvecx\!} = -\goverbrace{\left(\ve_r\PD{}{\rcol{r}}+\ve_\theta{1\over \rcol{r}}\PD{}{\thetacol{\theta}}\right)}^{\opcol{\vec \nabla}}\left(-{GMm\over \rcol{r}}\right)=-{GMm\over \rcol{r}^2}\ve_r \end{equation} となって$\vec F\,\kakko{\!\colvecx\!}$が出てくる（マイナス符号があるので$\ve_r$と逆向きすなわち引力である）。