指数関数
冪と指数
$x\times x={x}^2$,$x\times x\times x={x}^3$などと、同じ数を複数回掛ける計算を右肩に小さい字で回数を示して表すが、この${x}^2,{x}^3,{x}^4,\cdots$などの右肩の数字を「指数(exponent)」、冪乗されている方の数を「底(base)」と呼ぶ。$x^n$と書いたとき、$n$が指数で$x$が底である($底^{指数}$)。
「$\fbox{底}^{\fbox{指数}}$」は「$\fbox{底}$の$\fbox{指数}$乗」と読み、指数は同じ数$a$を何回掛算したかという数なので、
$$ a^{x_1}\times a^{x_2}=a^{x_1+x_2} $$ という法則が成り立つ。この式は「$a$を$x_1$回掛けたものと$a$を$x_2$回掛けたものの掛算は$a$を$x_1+x_2$回掛けたものだ」と主張している。同様に以下の法則も成り立つ。
\begin{equation} {a^{x_1}\over a^{x_2}}=a^{x_1-x_2} \end{equation}
指数の掛算については、
$$ \left( a^{x_1} \right)^{x_2} = a^{x_1x_2} $$ という式が成り立つ(指数の割算についてもこの後出てくる)。
ここまでの「指数」は掛けた回数なので、自然数でなくてはいけない。
冪で表された$\ycol{y}=\xcol{x}^n$の形の関数では、底$\xcol{x}$が独立変数であって指数$n$が関数の形を決めるパラメータとなっている。つまり$\ycol{(従属変数)}=\xcol{(独立変数)}^{(パラメータ)}$であった。
「指数関数」というのはこの指数の方が独立変数になって、$\ycol{(従属変数)}=(パラメータ)^{\xcol{(独立変数)}}$の形になっている(式の形は同じでも「何を変化させたときの変化が見たいのか」が違う関数である)。指数関数を$\ycol{y}=a^{\xcol{x}}$と表現すると、指数$\xcol{x}$が独立変数で、底$a$がパラメータである。
こういう関数が必要になる例は日常生活でもある。たとえば年10%の利子がつく借金があったとすると、最初10000円借りても、1年ほっておくと$10000\times 1.1=11000$円になる。2年めには12000円になるのではなく、$11000\times 1.1=12100$円になる(3年だと$12100\times 1.1=13310$円である)。この場合は$\xcol{x}$年経った時、借金は$\ycol{y}=10000\times 1.1^{\xcol{x}}$になっている(ちなみに10年だと25937.424601円である)。指数関数はこんなふうに「毎回同じ割合で増えていく(あるいは減っていく)」量に対して使われる。
関数という形にしたからには、$\ycol{y}=a^{\xcol{x}}$の$\xcol{x}$にはいろんな実数が代入できて欲しい。ここまでの指数は自然数であったが、以下でそれをいろんな数に拡張していく。
などの答えが出てきた。
例として、$\ycol{y}=2^{\xcol{x}}$という関数を考えて、まずは$\xcol{x}$が0以上の整数である場合(負の場合についてはすぐ後で考える)を考えると下のグラフのようになる。
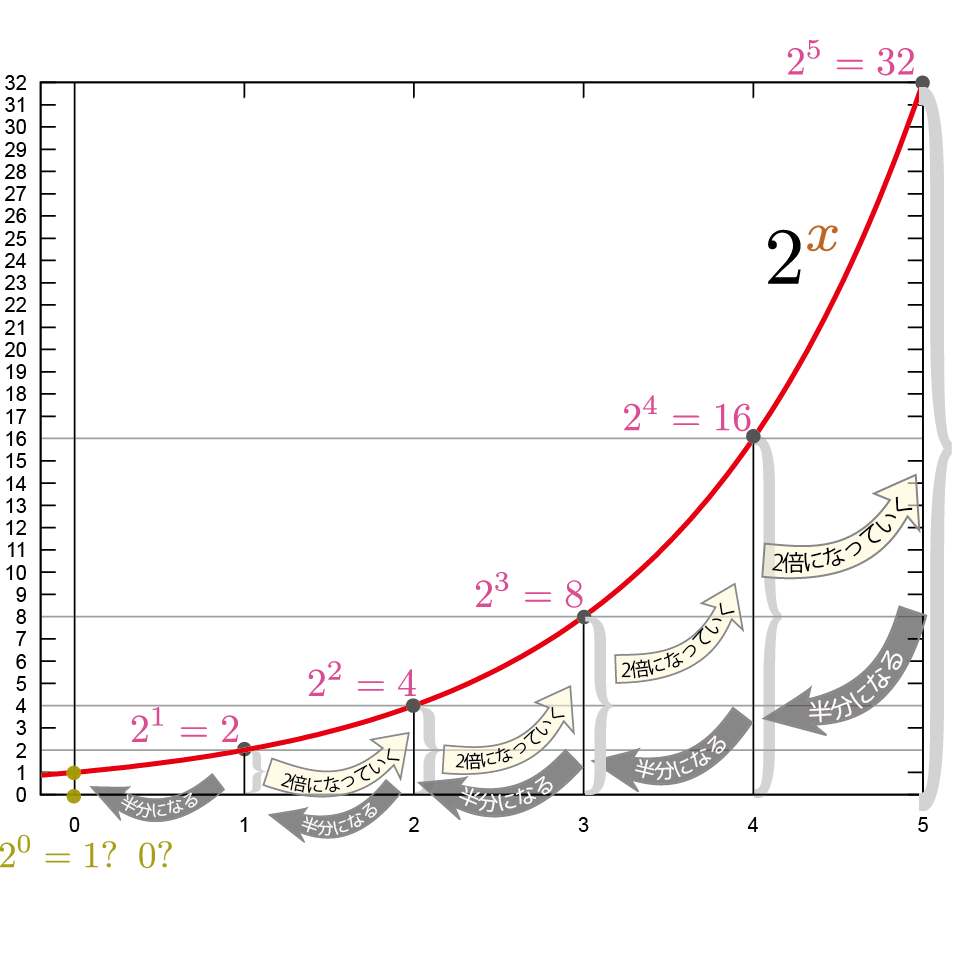
$\xcol{x}=0$のとき$\ycol{y}=1$である($2^0=1$)ことを不思議に思うかもしれない。「$2$を$0$回掛算したなら、答は0では??」と。
しかし上のグラフを見ると、この関数は「$\xcol{x}$が1増えると2倍になる」「$\xcol{x}$が1減ると半分になる」という変化をしている。だから、$\xcol{x}=1$から1減って$\xcol{x}=0$になれば、$\xcol{x}=1$のときの値である2の半分になる(つまり1になる)方が筋が通っている。
それに、$2^0=0$にしてしまうと、冪乗の積の式が、$x_1$もしくは$x_2$が0のときに成り立たなくなってしまう。$x_1=0$にするとこの式は \begin{equation} a^{x_1} \times a^{0}=a^{x_1+0} \end{equation} となるから、$a^0$は($a$が0でない、どんな数であろうが!)1でなくてはいけない。
いや、俺は$2^0=0$がいいねと思う人もいるかもしれない。どうしてもそうしたければ、$a^{x_1}\times a^{x_2}=a^{x_1+x_2}$という計算ルールは、指数が0のときを例外とする定義を使うしかない。なるべくなら例外のないルールの方がいいので、世間ではそうしていない。
以下で、この$x_1$や$x_2$を\fukidasi{自然数および0}以外の数にも拡張していこう。まず、$x_1$もしくは$x_2$が負の整数である場合はどうだろう?---グラフを$\xcol{x}$が負の領域まで伸ばしてみたのが
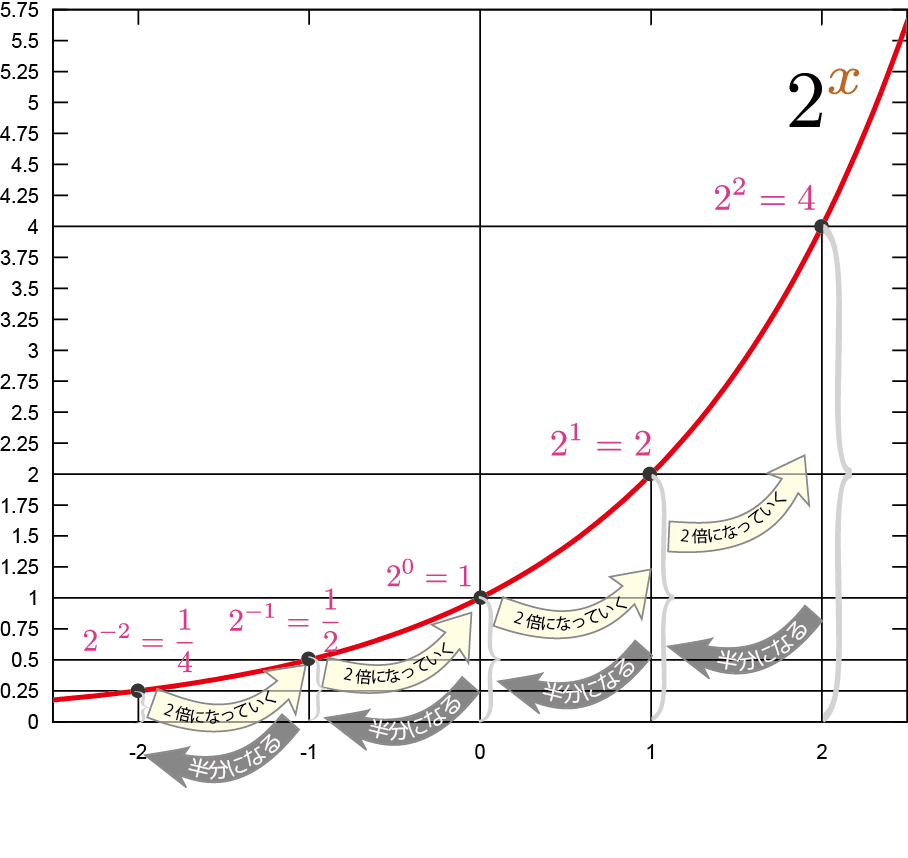
である。よって、$2^{-1}={1\over 2}$,$2^{-2}={1\over 4}$と半分にしていけばよいのではないかと思われる。
これは上の計算ルールに即している。確認しよう。 \begin{equation} \underbrace{2^{4}}_{16}\times 2^{-1}=2^{4-1}=2^3=8 \end{equation} という式が成立するためにも、$2^{-1}={1\over 2}$であればよいことがわかる。こうして、指数が負の数である場合は、$a^{-\xcol{x}}={1\over a^{\xcol{x}}}$とすればよいことになる。$2^{x}\times 2^{-x}=2^{x-x}=2^0$という式を書いてみれば、$2^0=1$の妥当性が再確認される。
$a^{x_1}\times a^{x_2}=a^{x_1+x_2}$という計算ルールを尊重するという立場に立てば、$a^{1\over 2}$や$a^{1\over 3}$(あるいは$a^{1\over 100}$だろうと)をどのように定義すべきかわかる。$a^{1\over 2}\times a^{1\over 2}=a$となるためには$a^{1\over 2}=\sqrt{a}$となる。同様に、$a^{1\over 3}=\sqrt[3]{a}$であり、$a^{1\over 100}=\sqrt[100]{a}$である。こうしてたとえば$a^{3.42}$という量を計算する方法を我々は知ることができる(たとえば100回掛けたら$a^{342}$になる数だと思えばよい---計算で求めるのはたいへんそうだが!そんなたいへんな計算も、後で出てくる\reftext{defoflog}{対数関数}や、微分やテイラー展開の助けを借りて計算できるようになる。)。こうして$a^{\xcol{x}}$という関数を$\xcol{x}$が小数、分数などで表現される有理数である場合について計算できるようになる。
では$\xcol{x}$が無理数である場合(たとえば$2^{\sqrt{2}}$は?---あるいは$5^\pi$は?)はどう考えようか。 たとえば、$\sqrt{2}\fallingdotseq1.41421356237\cdots$であるから、 \begin{equation} \begin{array}{rl} 2^1&=2\\ 2^{1.4}&\fallingdotseq 2.63901582\cdots \\ 2^{1.41}&\fallingdotseq 2.65737162\cdots \\ 2^{1.414}&\fallingdotseq 2.66474965\cdots \\ 2^{1.4142}&\fallingdotseq 2.66511909\cdots \\ 2^{1.41421}&\fallingdotseq 2.66513756\cdots\\ 2^{1.414213}&\fallingdotseq 2.66514310\cdots\\ &$\vdots \end{array} \end{equation} に並べたようにどんどん精度を上げつつ計算していけば、$2^{\sqrt{2}}$の値が計算できる。
指数関数の傾きとネイピア数
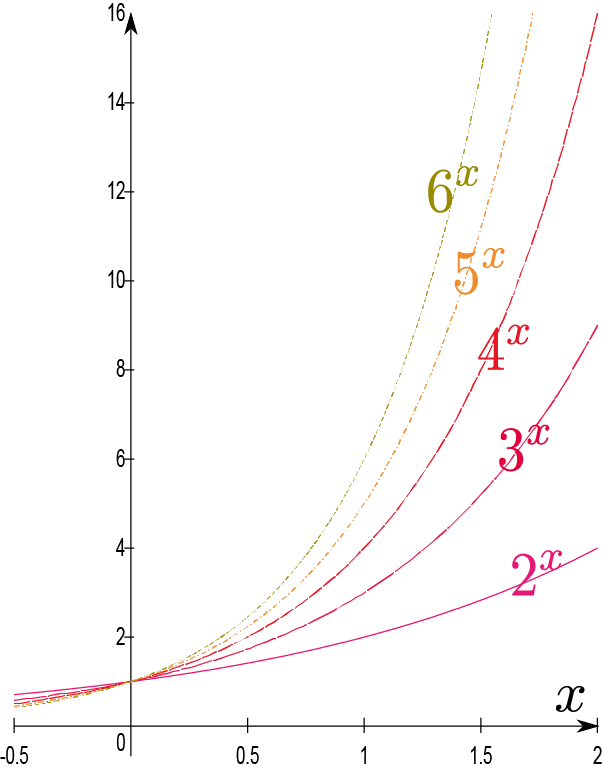
図は$2^{\xcol{x}},3^{\xcol{x}},4^{\xcol{x}},5^{\xcol{x}},6^{\xcol{x}}$のグラフで、$\xcol{x}$が増加するに従って急速に(グラフの傾きが大きくなりながら)増大していく関数であることが表現されている。そのため「指数関数的に増大する」という言葉はしばしば「手に負えないほど非常に速く増える」を意味するものとして使われる(既に述べたように借金の増大は指数関数的だから、放っておくと手に負えなくなる)。グラフは$\xcol{x}=2$までしか描かれていないが、例えば$\xcol{x}=10$では$2^{10}=1024$であり、右のグラフはあっという間に天井を突き抜けてしまう。さらに、$\xcol{x}=100$では$2^{100}=1267650600228229401496703205376$というとんでもない数字になる。
なお、動くグラフが
にある(授業ではこれを使った)。
底が大きくなると指数関数は増加の度合いが大きくなる。$a < 1$の場合は、むしろ減少する関数となる。$\left({1\over 2}\right)^{\xcol{x}}$のようにぐんぐん減る関数は「指数関数的に減衰(ダンプ)する」と表現する。
何度か強調しているが、「関数のある点の近傍でのふるまい」を考えることは重要である。そこで指数関数の$\xcol{x}=0$点付近でのふるまいを見ておこう。
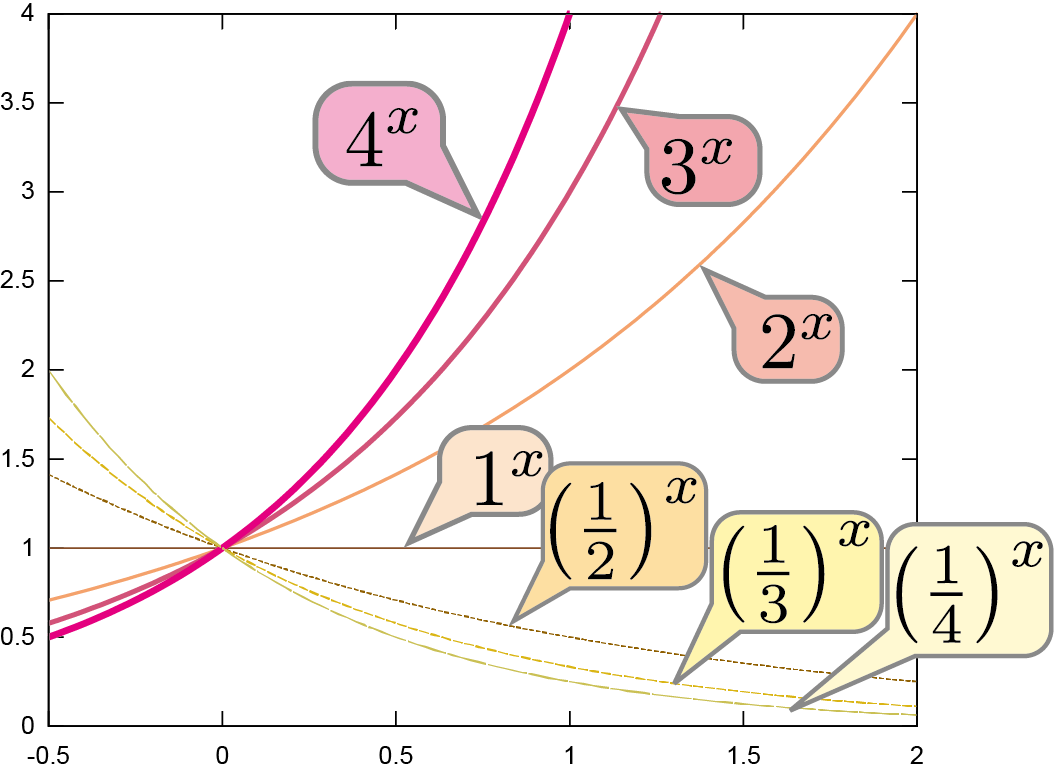
グラフにも示したように、$\xcol{x}=0$での$\ycol{y}=a^{\xcol{x}}$の値はすべての$a$で等しく1である。一方、$\xcol{x}=0$でのグラフの傾きは、底$a$が大きいほど大きい($a<1$では傾きは負)。
増加関数になる$a>1$の場合を考えて、$\xcol{x}=0$での傾きがちょうど1になる$a$を探す。そのときの$a$を$\E$と書いて「ネイピア数(Napier's constant)」もしくは「自然対数の底」と呼ぶ。シンプルに$\E$(イー)と呼んでいることも多い。変数$e$と区別するために、$\E$は立体で書く(イタリックにしない)ことにする。このあたりの流儀は本によって違う。
$\E$の大きさは$\E=2.718281828459045\cdots$である。この$\E$は無理数であることが証明されていて、無限に続く小数である。この値をどうやって計算するのかについては、ここでは「いろんな値を入れてグラフを描いていき、傾きが1になるところを探せば$\E$は計算できるだろう」という程度の大雑把な理解にとどめておこう}。なぜ傾き1がそんなに大事なのかについては後でわかるが、ここでは「傾きはすなわち微分であり、微分を知ることが自然法則を知る手がかりになる」とだけ指摘しておく(微分の勉強まで進んだところで、その意味がわかるだろう)。そういうわけで、数ある指数関数の中でも、$\E^\xcol{x}$という形の指数関数は今後もっとも頻繁に登場する。
電卓で$\E$を計算する方法
まず$\fbox{1}$を押して次に$\fbox{M+}$を2回押す(この段階で電卓のメモリには$1+1$が入っている)。次にそこにある1を2で割る。結果($0.5$)が出たところで、また$\fbox{M+}$を押す(これで$1+1+{1\over 2}$)。次に3で割って$\fbox{M+}$(これで$1+1+{1\over 2}+{1\over 2\times3}$)、さらに4で割って$\fbox{M+}\cdots$と繰り返す(${1\over n!}$を順番に計算しては足している)。電卓の精度以下の数字になったところで$\fbox{MR}$を押すとこれまで$\fbox{M+}$でメモリに入れた数字の和が出てくるが、その値は$\E=2.718281828\cdots$になっているはずだ。
上のようにして$\E$が計算できる理由は、後で出てくる(だからまだわからなくてもよい)、「$\E^\xcol{x}$のテイラー展開の式」$\E^{\xcol{x}}=1+\xcol{x}+{\xcol{x}^2\over 2!}+{\xcol{x}^3\over 3!}+{\xcol{x}^4\over 4!}+{\xcol{x}^5\over 5!}+\cdots$があって、その式に$\xcol{x}=1$を代入すると、 \begin{equation} \E = 1+1+{1\over 2!}+{1\over 3!}+{1\over 4!}+{1\over 5!}+\cdots \end{equation} になるからである。この式がどうやって出てくるかは後のお楽しみであるが、とりあえず$\E^{\xcol{x}}=1+\xcol{x}+\cdots$までは「$\xcol{x}=0$での値が1で傾きが1」からわかる。