偏微分方程式
偏微分方程式と常微分方程式
ここまでの微分方程式は常微分$\left(\ddx,\left(\ddx\right)^2,\ldots\right)$を用いた微分方程式だった。偏微分$\left(\PD{}{\xcol{x}},\PD{}{\ycol{y}},\PD{}{\tcol{t}},\ldots\right)$を用いた微分方程式、「偏微分方程式」を考えよう。
常微分方程式の場合、積分していくことで解が求められた。そのときに積分定数という形で解に未定のパラメータが入った。たとえば常微分方程式$\ddx f\kakko{\xcol{x}}=\xcol{x}$の解は$f\kakko{\xcol{x}}={\xcol{x}^2\over 2}+C$である。これに似た偏微分方程式$\PD{}{\xcol{x}}f\kakko{\xcol{x},\ycol{y}}=\xcol{x}$の解は$f\kakko{\xcol{x},\ycol{y}}={\xcol{x}^2\over 2}+C\kakko{\ycol{y}}$である。偏微分方程式もこのように積分していくことで解を求めることができるが、出てくる「積分定数」にあたるものが常微分方程式とはかなり違う。
常微分方程式なら独立変数(たとえば$\xcol{x}$)の積分により解が出たから、$\xcol{x}$に依らない積分定数が解に現れた。$(\xcol{x},\ycol{y})$の二つの独立変数を持つ偏微分方程式では$\xcol{x}$の積分によって現れた積分定数は$\ycol{y}$の関数であってよい(逆に$\ycol{y}$の積分による積分定数は$\xcol{x}$の関数であってよい)。
「微分して0$\Rightarrow$定数」ではないことが偏微分方程式の注意点である。
もう少しだけ複雑な例、 \begin{equation} \left(\PD{}{\xcol{x}}+a\PD{}{\ycol{y}}\right)f\kakko{\xcol{x},\ycol{y}}=0\label{axyPDEzero} \end{equation} を考えよう。これの解の一つが$a\xcol{x}-\ycol{y}$であることはすぐに確認できるが、実は$g$を任意の1変数関数として、その引数に$a\xcol{x}-\ycol{y}$が代入された$g\,\kakko{a\xcol{x}-\ycol{y}}$も解になる。というのは$g\,\kakko{a\xcol{x}-\ycol{y}}$を、「$\ycol{y}$を一定にして$\xcol{x}$で偏微分」したものと「$\xcol{x}$を一定にして$\ycol{y}$で偏微分したもの」は$-a$倍違うから、 \begin{equation} \left(\PD{}{\xcol{x}}+a\PD{}{\ycol{y}}\right)g\,\kakko{a\xcol{x}-\ycol{y}}=0 \label{axyPDE} \end{equation} が成立するからである。たとえば$\tan\kakko{a\xcol{x}-\ycol{y}}$でも$\log\kakko{a\xcol{x}-\ycol{y}}$でも、あるいは${(a\xcol{x}-\ycol{y})^5\over \sqrt{\sin(a\xcol{x}-\ycol{y})}}$のような複雑な関数でも、この偏微分方程式の解となる分母が0になったりルート内が負になったりする領域が省かれるのはもちろんである。。このような変数の組み合わせを見つけるというのも偏微分方程式の解き方である。
偏微分方程式の解き方
変数分離による解法
\begin{equation} \left(\PD{}{\xcol{x}},\PD{}{\ycol{y}}を含む微分演算子\right)f\kakko{\xcol{x},\ycol{y}}=g\,\kakko{\xcol{x},\ycol{y}} \end{equation} のような微分方程式が与えられたとき、これの解をいきなり探すのは難しい。そこで、この方程式の解が$f\kakko{\xcol{x},\ycol{y}}=X\kakko{\xcol{x}}Y\kakko{\ycol{y}}$のように$\xcol{x}$を変数とする部分と$\ycol{y}$を変数とする部分の積になるだろう、と仮定してみる。その後計算した結果、 \begin{equation} \left(\PD{}{\xcol{x}}と\xcol{x},X\kakko{\xcol{x}}の式\right) = \left(\PD{}{\ycol{y}}と\ycol{y},Y\kakko{\ycol{y}}の式\right)\label{PDEbunri} \end{equation} のように左辺と右辺に$\xcol{x}$と$\ycol{y}$が分離できたとする(これを「変数分離」変数を分けているという意味では常微分での「変数分離」と同様ではあるが、この場合は$\xcol{x}$と$\ycol{y}$が独立なので、この後の計算の仕方は違う。と呼ぶ)。この形になった結果、微分は偏微分ではなく常微分となるそもそも偏微分は複数の変数があるときに一つの変数以外を固定する微分だから、変数が一つしかないなら偏微分と常微分に区別はない。。結局解くべきは \begin{equation} \left(\ddx と\xcol{x},X\kakko{\xcol{x}}の式\right) = \left(\ddy と\ycol{y},Y\kakko{\ycol{y}}の式\right)\label{PDEbunritwo} \end{equation} という式になるが、この式が成立するためには左辺も右辺も定数にならなくてはいけない$\xcol{x}$と$\ycol{y}$は独立変数で、勝手に変化できるのだから、左辺が$\xcol{x}$によって変化し、右辺が$\ycol{y}$によって変化したら、この式は運がいいときにしか成立しない式になる。ので、 \begin{equation} \left(\ddx と\xcol{x},X\kakko{\xcol{x}}の式\right)=\alpha,~~ \left(\ddy と\ycol{y},Y\kakko{\ycol{y}}の式\right)=\alpha \end{equation} とする。ただし$\alpha$はまだ決まっていない定数である。こうして偏微分方程式を常微分方程式二つに分けるのが「偏微分方程式の変数分離」である。なお、変数分離で答が求まるというのはあくまで「仮定」であるから、これで正しい解が出ているかどうかについては注意しなくてはいけない。
$\alpha$は任意の定数だから、その定数に応じてたくさんの解が出るが、境界条件などにより実際の解がどのようになるかが決められる(このあたりは常微分方程式でもあったこと)。
一例として、さっきの$\left(\PD{}{\xcol{x}}+a\PD{}{\ycol{y}}\right)f\kakko{\xcol{x},\ycol{y}}=0$を変数分離で解いてみよう。
$f\kakko{\xcol{x},\ycol{y}}=X\kakko{\xcol{x}}Y\kakko{\ycol{y}}$とすると \begin{equation} \begin{array}{rl} \ddx X\kakko{\xcol{x}}Y\kakko{\ycol{y}}+aX\kakko{\xcol{x}}\ddy Y\kakko{\ycol{y}}= &0 \\ {\displaystyle \ddx X\kakko{\xcol{x}}\over X\kakko{\xcol{x}}} =& -a{\displaystyle\ddy{Y\kakko{\ycol{y}}}\over Y\kakko{\ycol{y}}} \\ \end{array} \end{equation} と変数分離され、$\alpha$を任意の数として、 \begin{equation} {\displaystyle \ddx X\kakko{\xcol{x}}\over X\kakko{\xcol{x}}}=\alpha,~~~ -a{\displaystyle \ddy Y\kakko{\ycol{y}}\over Y\kakko{\ycol{y}}}=\alpha \end{equation} という二つの式になる。それぞれ解けば \begin{equation} X\kakko{\xcol{x}}=C\E^{\alpha\xcol{x}},~~~Y\kakko{\ycol{y}}=D\E^{-{\alpha\over a}\ycol{y}} \end{equation} という解が出る。よって以下の答えが出る。 \begin{equation} f\kakko{\xcol{x},\ycol{y}}=CD\E^{{\alpha\over a}\left(a\xcol{x}-\ycol{y}\right)}\label{PDEsolone} \end{equation} この微分方程式は線形斉次であり、線形斉次ならば重ね合わせができるのは偏微分方程式でも同じである。$\alpha$が違うそれぞれの解について係数は任意であるから、$CD$となっていた定数を$c_\alpha$と置き、さまざまな$\alpha$の値で足し合わせることで \begin{equation} f\kakko{\xcol{x},\ycol{y}}=\sum_{\alpha}c_\alpha\E^{{\alpha\over a}\left(a\xcol{x}-\ycol{y}\right)} \end{equation} という解ができる。
この微分方程式の解は$a\xcol{x}-{\ycol{y}}$の任意の関数になることはすでに述べた。それに比べて上の式は「任意の関数」になっていないように思われるかもしれないが、この場合$\alpha$が任意(複素数でも構わない)なのでいろんな値の$\alpha$の解を重ね合わせることで任意の関数を作ることができる。
特性曲線による解法
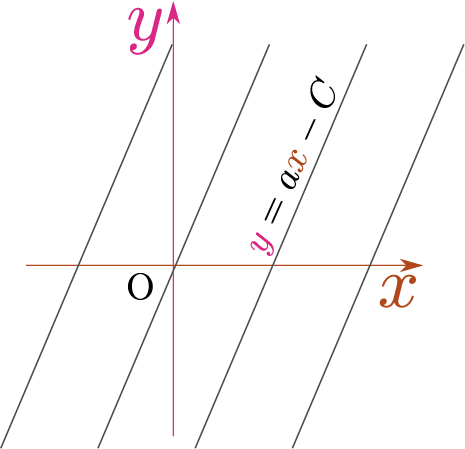
$\left(\PD{}{\xcol{x}}+a\PD{}{\ycol{y}}\right)f\kakko{\xcol{x},\ycol{y}}=0$を解いて「$a\xcol{x}-{\ycol{y}}$の任意の関数」という形で解を得た。この結果を「この方程式の解$g\,\kakko{a\xcol{x}-\ycol{y}}$は直線$\ycol{y}=a\xcol{x}-C$($C$は定数)この直線の上では$a\xcol{x}-\ycol{y}$が一定なのはもちろんのことである。の上で一定の値を取る」と表現してもよい。より一般的には「偏微分方程式の解はある曲線の上で一定の値を取る」という形で表現することができる。上の場合「直線」の上で解となる関数が一定となったが、 \begin{equation} \left( P\,\kakko{\xcol{x},\ycol{y}}\PD{}{\xcol{x}} + Q\,\kakko{\xcol{x},\ycol{y}}\PD{}{\ycol{y}} \right)f\kakko{\xcol{x},\ycol{y}}=0 \end{equation} のような偏微分方程式の場合、解である関数$G\kakko{\xcol{x},\ycol{y}}$を一つ見つけることができたなら、任意の関数$g\,\kakko{\tcol{t}}$の$\tcol{t}$に$G\kakko{\xcol{x},\ycol{y}}$を代入した$g\,\kakko{G\kakko{\xcol{x},\ycol{y}}}$もやはり解となる。この場合は、$G\kakko{\xcol{x},\ycol{y}}=C$(定数)であるような線の上で$g$は一定となる。このような線を(上の例では直線だが、直線とは限らないので)「特性曲線(characteristic curve)」と呼ぶ。特性曲線を求めることも、偏微分方程式の解法と言える。< 微分方程式 \begin{equation} \left(\PD{}{\xcol{x}}+2\xcol{x}\PD{}{\ycol{y}}\right)f\kakko{\xcol{x},\ycol{y}}=0\label{tokuseihoubutsu} \end{equation} は特性曲線が文字通り曲線になる例である。
ここまで何度も「偏微分には方向がある」と(少々くどく)述べたが、ここで述べた微分方程式の解き方は偏微分が0になる方向を探すという方針の解き方である。
では、具体的な例を少しだけやってみよう。
熱伝導方程式
次の微分方程式(熱伝導方程式)は、1次元的な物体(細い棒など、断面積が無視できるような物体)の温度を表す関数の満たす微分方程式である。$\tau\kakko{\tcol{t},\xcol{x}}$は時刻$\tcol{t}$の場所$\xcol{x}$における温度を表す$\tau$はギリシャ文字の t に対応する文字。温度(temperature)だから$t$を使いたいところだが、$t$は時間に使っているし、$T$も別の意味で使うのでギリシャ文字に登場願う。。

\begin{equation} \PDC{\tau(\tcol{t},\xcol{x})}{t}{\xcol{x}} =K\PPDC{\tau(\tcol{t},\xcol{x})}{\xcol{x}}{\tcol{t}}\label{dendou} \end{equation} この式にはどんな意味があるのかを図解しておこう。右辺は$\xcol{x}$に関する二階微分である二階微分はグラフの曲がり具合という意味を持っていたことを思い出そう。。すなわち($\tcol{t}$を一定として描いた)$\xcol{x}$-$\tau$グラフの曲がり具合である。
$\PPDC{\tau(\tcol{t},\xcol{x})}{\xcol{x}}{\tcol{t}}$が正ならそこで下に凸、負ならそこで上に凸なグラフとなる。図に示したように、二階微分が正であることは「自分の両サイドの平均に比べて、自分の温度が低い」という状況を表している。このような時は温度は上がるだろう(二階微分が負であるときはこの逆)。温度変化が線形(グラフが直線)のときは温度が時間変化しない「流れてくる熱」が傾きすなわち一階微分に比例して決まると考えるとこうなるのはもっともである。グラフが直線になるとき、「温度が高い(温かい)方から流れてくる熱と、温度が低い(冷たい)方に奪われる熱が平衡している」という状況になる。実際には流れてくる熱量はもっと複雑な関数であろうが、線形近似できる範囲では温度差に比例するとして差し支えない。。
変数分離による一般解
この式を変数分離で解く。すなわち、$\tau\kakko{\tcol{t},\xcol{x}}$をいきなり考えるのは難しいので、 \begin{equation} \tau\kakko{\tcol{t},\xcol{x}}=T\kakko{\tcol{t}}X\kakko{\xcol{x}} \end{equation} のように、$\tcol{t}$の関数の部分と$\xcol{x}$の関数の部分の積で表現されていると仮定する。これを代入してみると、 \begin{equation} \PDC{\left(T\kakko{\tcol{t}}X\kakko{\xcol{x}}\right)}{\tcol{t}}{\xcol{x}} =K\PPDC{\left(T\kakko{\tcol{t}}X\kakko{\xcol{x}}\right)}{\xcol{x}}{\tcol{t}} \end{equation} となる。左辺の$\tcol{t}$による微分は$T\kakko{\tcol{t}}$にだけ掛かり、右辺の$\xcol{x}$による微分は$X\kakko{\xcol{x}}$にだけ掛かる(よってここから先の微分は偏微分ではなく常微分となる)。結果は \begin{equation} \begin{array}{rll} X\kakko{\xcol{x}}{\ddt T}\kakko{\tcol{t}}=&K T\kakko{\tcol{t}}{\left(\ddx\right)^2 X}\kakko{\xcol{x}}\\[3mm] {\displaystyle{\ddt T}\kakko{\tcol{t}}\over T\kakko{\tcol{t}}}=&K {\displaystyle{\left(\ddx\right)^2 X}\kakko{\xcol{x}}\over X\kakko{\xcol{x}}} \end{array}\label{heatbunri} \end{equation} のようになる。整理して左辺に$\tcol{t}$に関連する量が集まるようにした。
ここで、左辺と右辺が定数$\alpha$になると考えて、 \begin{equation} \begin{array}{rl} {\displaystyle{\ddt T}\kakko{\tcol{t}}\over T\kakko{\tcol{t}}}=\alpha~~~ &すなわち ~~~ {\ddt T}\kakko{\tcol{t}}=\alpha T\kakko{\tcol{t}},\\[4mm] K {{\displaystyle \left(\ddx\right)^2 X}\kakko{\xcol{x}}\over X\kakko{\xcol{x}}}=\alpha ~~~&すなわち~~~ {\left(\ddx\right)^2 X}\kakko{\xcol{x}}={\alpha\over K}X\kakko{\xcol{x}} \end{array} \end{equation} の二つの常微分方程式を解けばよい。どちらも定数係数の線形斉次微分方程式だから、結果は \begin{equation} T\kakko{\tcol{t}}= A \E^{\alpha\tcol{t}},~~X\kakko{\xcol{x}}=B \E^{\sqrt{{\alpha\over K}}\xcol{x}} +C \E^{-\sqrt{{\alpha\over K}}\xcol{x}} \end{equation} と簡単に求まるほんとは$\alpha=0$の場合を特別扱いする必要があるがここではそれは無視する。教科書にはちゃんと書いてあるので気になる人はそちらを参照、まとめると、 \begin{equation} \tau\kakko{\tcol{t},\xcol{x}}= \E^{\alpha\tcol{t}}\left( F \E^{\sqrt{{\alpha\over K}}\xcol{x}} +G \E^{-\sqrt{{\alpha\over K}}\xcol{x}} \right) \end{equation} となる。さまざまな$\alpha$の値全てに対して一個ずつ解がある。
線形微分方程式なので、実際の解はいろんな$\alpha$の解に対する和であり、 \begin{equation} \tau\kakko{\tcol{t},\xcol{x}}= H\xcol{x}+J +\sum_{\alpha}\left( \E^{\alpha\tcol{t}}\left( F_\alpha \E^{\sqrt{{\alpha\over K}}\xcol{x}} +G_\alpha \E^{-\sqrt{{\alpha\over K}}\xcol{x}} \right)\right)\label{heatsolnobc} \end{equation} と書くことができる。係数$F,G$は各々の$\alpha$(ただし$\neq0$)の値に対して別々に存在するので、$F_\alpha,G_\alpha$と添字をつけて区別することにした。
これで境界条件を指定しない場合の解を求めることができた。
境界条件と初期条件
係数を決めるためには初期条件と境界条件が必要である。
教科書にはいろんな境界条件の場合をやっているが、授業ではその一つのディリクレ型だけを考えた。
ここでは境界は$\xcol{x}=0$と$\xcol{x}=L$だとしよう。境界条件は考えている現象に応じて選ばなくてはいけないが、よく使われる例として以下の「ディリクレ型境界条件(Dirichlet boundary condition)」を考えるディリクレ型は「固定端境界条件(fixed end boundary condition)」と呼ぶこともある。。
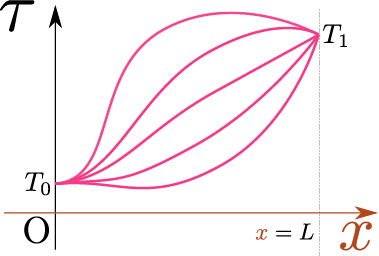
\begin{equation} \begin{array}{rl} \tau\kakko{\tcol{t},\xcol{x}=0}&=T_0,\\[4mm] \tau\kakko{\tcol{t},\xcol{x}=L}&=T_1 \end{array} \end{equation}
熱伝導の場合、ディリクレ型は「境界部分の温度は一定という条件(等温条件)」になる。
簡単な例として、ディリクレ型でかつ$T_0=T_1=0$という場合について解いてみよう。条件$\tau\kakko{\tcol{t},\xcol{x}=0}=0$を入れると \begin{equation} \tau\kakko{\tcol{t},\xcol{x}=0}= \E^{\alpha\tcol{t}}\left( F_\alpha +G_\alpha \right) \end{equation} となるがこれは全ての$\alpha$に対して$F_\alpha+G_\alpha=0$を意味するので、この段階で \begin{equation} \tau(\tcol{t},\xcol{x})=\sum_\alpha F_\alpha\E^{\alpha\tcol{t}}\left( \E^{\sqrt{{\alpha\over K}}\xcol{x}} -\E^{-\sqrt{{\alpha\over K}}\xcol{x}} \right)+H\xcol{x}\label{katahoukotei} \end{equation} という形でなくてはならないことがわかる。次に$\xcol{x}=L$での条件を考えると、 \begin{equation} \tau\kakko{\tcol{t},\xcol{x}=L}=\sum_\alpha F_\alpha\E^{\alpha\tcol{t}}\left( \E^{\sqrt{{\alpha\over K}}L} -\E^{-\sqrt{{\alpha\over K}}L} \right)+ HL=0\label{ryouhoukotei} \end{equation} となるが、任意の時刻で0になるためには、$H=0$かつ、全ての$\alpha$に対して \begin{equation} \E^{\sqrt{{\alpha\over K}}L} -\E^{-\sqrt{{\alpha\over K}}L}=0 \end{equation} となる必要がある。上の式を変形すると$\E^{2\sqrt{{\alpha\over K}}L}=1$である。「$\E^0=1$だから$2\sqrt{{\alpha\over K}}L=0$」と考えてしまうと$\alpha=0$だが、今は$\alpha\neq0$の場合のみ考えよう。実は$\ncol{n}$が整数のとき、$\E^{2\ncol{n}\pi\mathrm i}=1$\label{exptwopii}という式があるから、$\alpha$は0ではなく、 \begin{equation} 2\sqrt{{\alpha\over K}}L=2\ncol{n}\pi\I~~~すなわち、\alpha=-{\ncol{n}^2\pi^2 K\over L^2} \end{equation} のように決まる$\alpha$は連続的な量ではなく離散的な量である。こうなることを知っていたので、$\sum_\alpha$のように和を書いた。。この条件から$\sqrt{{\alpha\over K}}= \I{\ncol{n}\pi\over L}$として代入する「えっ、虚数にしていいの?」とびっくりする人がいるかもしれないが、この場合も、最終結果が実数になるように調整すれば別に問題はない。と、 \begin{equation} \tau\kakko{\tcol{t},\xcol{x}} =\sum_{\ncol{n}\neq0}\tilde F_\ncol{n} \E^{-{\ncol{n}^2\pi^2K\over L^2}\tcol{t}}\gunderbrace{\left( \E^{\mathrm i{\ncol{n}\pi\over L}\xcol{x}} -\E^{-\mathrm i{\ncol{n}\pi\over L}\xcol{x}} \right)}_{2\I\sin{\ncol{n}\pi\over L}\xcol{x}} =\sum_{\ncol{n}>0}\gunderbrace{\left(2\I \tilde F_\ncol{n}-2\I\tilde F_{-\ncol{n}}\right)}_{\tau_{\ncol{n}}と書く} \E^{-{\ncol{n}^2\pi^2 K\over L^2}\tcol{t}}\sin {\ncol{n}\pi\over L}\xcol{x}\label{twoiF} \end{equation} \noindent が境界条件を満たす一般解であるここで使った$\tilde ~$という記号は「チルダ」という記号で、$\tilde F$は「えふちるだ」と読む。「$F$とはちょっと違う関数だよ」を示すために使う(どのように違うかは状況によりさまざまである)。}。ここで、$\alpha$が$\ncol{n}^2\times(定数係数)$という形になったので、$F_\alpha$を$\tilde F_\ncol{n}$と書き直した。
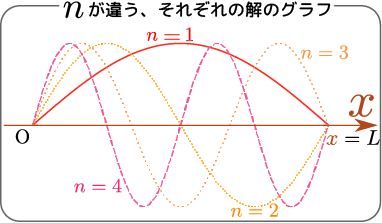
結果はさまざまな$\ncol{n}$に関する$\sin{\ncol{n}\pi\over L}\xcol{x}$に定数を掛けた項の和になっているが、$\sin$は奇関数で$\ncol{n}\to -\ncol{n}$と置き換えても本質的に同じ(符号が違うだけ)であるので、和を一つにまとめることにし、$\sum_{\ncol{n}>0}$とし、代わりに$2\I \tilde F_\ncol{n}\to 2\I\tilde F_\ncol{n}-2\I\tilde F_{-\ncol{n}}$と置き換えた。以下、$2\I \tilde F_\ncol{n}-2\I\tilde F_{-\ncol{n}}=\tau_\ncol{n}$($\tau_\ncol{n}$は実数)と書こう。
微分方程式の解としては、初期条件今考えている微分方程式は時間に関しては一階だから、初期条件は一つでいい。ただし、それは「$\tcol{t}$の微分方程式として」の話なので、「$\xcol{x}$の一つの値に対して一つの境界条件」が必要。も満たさなくてはいけない。$\tau\kakko{\tcol{t}=0,\xcol{x}}=\tau_初\kakko{\xcol{x}}$を初期条件とする($\tau_初\kakko{\xcol{x}}$は与えられた関数である)と、 \begin{equation} \tau_初\kakko{\xcol{x}}=\sum_{\ncol{n}>0}\tau_\ncol{n}\sin{\ncol{n}\pi\over L}\xcol{x} \end{equation} になるように係数$\tau_\ncol{n}$を決めればよい。
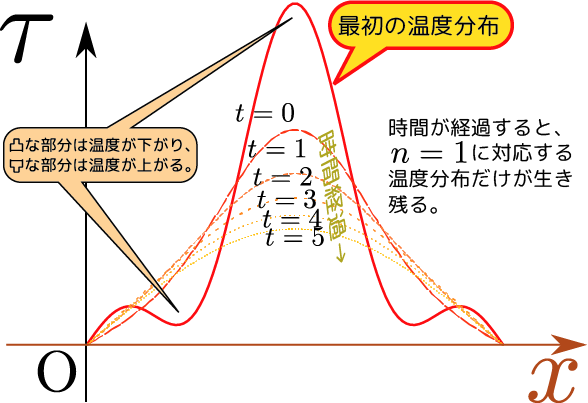
ここで、 \begin{equation} \tau\kakko{\tcol{t},\xcol{x}}=\sum_{\ncol{n}>0}\tau_\ncol{n} \E^{-{\ncol{n}^2\pi^2 K\over L^2}\tcol{t}}\sin{\ncol{n}\pi\over L}\xcol{x} \end{equation} という式の物理的意味について考えておこう。この式には$\E^{-{\ncol{n}^2\pi^2K\over L^2}\tcol{t}}$がついているから、時間が経てば経つほど、温度は0に近づいていく。今考えている状況は両端が温度0で、他に熱源はないのだから、十分に時間経過すれば全体の温度が0になるというのは「もっとも」なことである。$\ncol{n}$の違いはグラフで書いた時の「波の数」なので、より短い波長の温度分布(つまり頻繁に寒暖が入れ替わっている)ときに「早く冷める」というのは感覚的にも納得できるだろう。
熱伝導方程式のアニメーションは↓にある。
波動方程式
少し違う偏微分方程式 \begin{equation} \PPDC{u\kakko{\tcol{t},\xcol{x}}}{\tcol{t}}{\xcol{x}} =v^2\PPDC{u\kakko{\tcol{t},\xcol{x}}}{\xcol{x}}{\tcol{t}}\label{hadou} \end{equation} はこれは音などの「波」の方程式である。左辺は時間の二階微分だから加速度で、それは波の媒質(考えている波が音ならば空気、海の波なら海水)に働く力に比例する。右辺は力に比例するのだが、それが$\xcol{x}$に関する二階微分になっている。二階微分は「曲がり具合」を意味するのであった。ここで海にできる波をイメージして、$u\kakko{\tcol{t},\xcol{x}}$はある時刻におけるある場所の海面の高さだとしよう。右辺の$\xcol{x}$による二階微分は「海面の曲がり具合」を意味する。それが正なら海面は「谷」になり、負なら「山」になっていると思えばよい。海の波においては「山」なら下向きの、「谷」なら上向きの力が働くだろう、と考えると上の式の意味がわかる。熱伝導方程式では$\xcol{x}$の二階微分がそのまま温度の時間変化になったが、波の方程式の場合は「時間変化の時間変化」(すなわち加速度)になる。
時間に関して二階微分の方程式なので「慣性」が働いて波動になるのである。
というわけで授業はこれで終わり。来週はテストです。「試験範囲は?」という質問がありましたが、「やったところ全部」です。授業で飛ばしたところは出ません。
前期同様、「A4の紙1枚(何が書いてあっても可)」が持ち込み可能です。