指数関数と対数関数(続き)
指数関数の底の変換
$\ycol{y}=2^{\xcol{x}}$という関数と$\ycol{y}=4^{\tcol{X}}$という関数を考えよう。$\xcol{x}=2\tcol{X}$ならばこの二つが等しい。 \begin{equation} 2^{\xcol{x}}= 2^{2\tcol{X}}= (2^2)^\tcol{X}=4^\tcol{X} \end{equation} だからである(たとえば、$2\times 2\times 2\times 2=(2\times 2)\times(2\times2)=4^2$)。また$\xcol{x}={1\over 2}\ycol{Y}$ならば \begin{equation} 2^{\xcol{x}}= 2^{0.5\ycol{Y}}=\left(\sqrt{2}\right)^{\ycol{Y}} \end{equation} ということも言える。以上のように、指数を定数倍することは底を変えることと同じ操作になる。
今は2や4という単純な例で考えたが、もっと一般的に$\ycol{y}=a^\xcol{x}$と$\ycol{y}=b^\tcol{X}$の関係を考えよう。たとえば、$a$と$b$の間に$a=b^c$($c$もまた別の定数)という関係があるなら、 \begin{equation} a^\xcol{x}= (b^c)^\xcol{x}=b^{c\xcol{x}} \end{equation} となるから、$\tcol{X}=c\xcol{x}$とすればこの二つの関数が同じ関数になる。
指数関数の底はいろんな値を使ってよいが、日常計算においては$\ycol{y}=10^\xcol{x}$のように10が使われることが多い。一方、コンピュータや情報科学の世界では$\ycol{y}=2^\xcol{x}$のように2がよく使われる。
これも後でわかることだが、微分や積分などを行うには$\E$を底にした指数関数$\ycol{y}=\E^\xcol{x}$がもっとも使いやすい。よってこれらを互いに変換する必要がある。そのときに
指数関数の底を変える
$a=b^c$なら、 \begin{equation} a^\xcol{x}=b^{c\xcol{x}} \end{equation}
という方法を使う。たとえば$10=2^{3.321928094887362\cdots}$なので$10^3=1000,2^{10}=1024$だから$10^3\fallingdotseq2^{10}$である(コンピュータの世界で「キロ」と言ったら1000ではなく1024を指すことが多い)。ゆえに$10\fallingdotseq 2^{10\over3}$。、 \begin{equation} 10^{\xcol{x}}=2^{(3.321928094887362\cdots)\times \xcol{x}} \end{equation} となる。この${3.321928094887362\cdots}$という数字は10は2の何乗か?という疑問の答えであるが、それも一つの関数である。この関数は次の節で考える。
ここでテキストではちょっと戻って、
という問題を考えた。
1光年$\simeq 10^{16}$mなので、だいたい$10^9$光年(10億光年)。
というのが驚愕の答え。
対数関数
対数関数:指数関数の逆関数
前節の最後で「10は2の何乗か?」という疑問を考えた。より一般的に「$\xcol{x}$は$\kuro{a}$の何乗か?」という問題を考える。$\xcol{x}=a^\ycol{y}$という式が成り立つときに、$\xcol{x}\to\ycol{y}$という対応関係を知りたい。今考えたい関数は指数関数$\ycol{y}=a^\xcol{x}$の逆関数であり、これを「対数関数」と呼ぶ。対数関数を表現するには、$\log$という記号を使う$\log$も「関数の名前」だと考えればよい。よって、$\ycol{y}=f\kakko{\xcol{x}}$に合わせれば$\ycol{y}=\log\kakko{\xcol{x}}$のように$\kakko{}$を使って表現すべきだが、括弧はつけないことが多い。。一般的定義は
対数関数
1ではない正の定数$a$を底とする指数関数$\ycol{y}=a^{\xcol{x}}$($\xcol{x}$が独立変数で$\ycol{y}$が従属変数)に対し、$\ycol{y}$を先に決めてそれに対応する$\xcol{x}$を対応させる関数を対数関数といい、 \begin{equation} \xcol{x}=\log_a \ycol{y} \end{equation} と書く(この式では、$\ycol{y}$が独立変数で$\xcol{x}$が従属変数)。
$\log_a\xcol{x}$の$a$のことを指数関数のときと同様、「底(てい)」と呼ぶ。$\xcol{x}$の方は「真数」と呼ばれる(対数関数の値$=\log_{底}\kakko{真数}$)。$\log_{10}\xcol{x}$のように底を10にした対数関数を「常用対数」と呼ぶ。$\E$を底にした対数関数$\log_\E\xcol{x}$は「自然対数」である。以後、$\log\xcol{x}$のように底を省略した場合は自然対数とする。すなわち、省略された底は$\E$である分野によっては、$\log$と書いたときの底が10であったり2であったりする。「自然(natural)」のnを取って、$\log_\E \xcol{x}=\ln \xcol{x}$のように書くこともある。。
底が$2,\E,10$およびその逆数${1\over 2},{1\over \E},{1\over 10}$の場合の指数関数(実線)と対数関数(破線)のグラフを下に示した(互いに逆関数になっていることを確認せよ)。
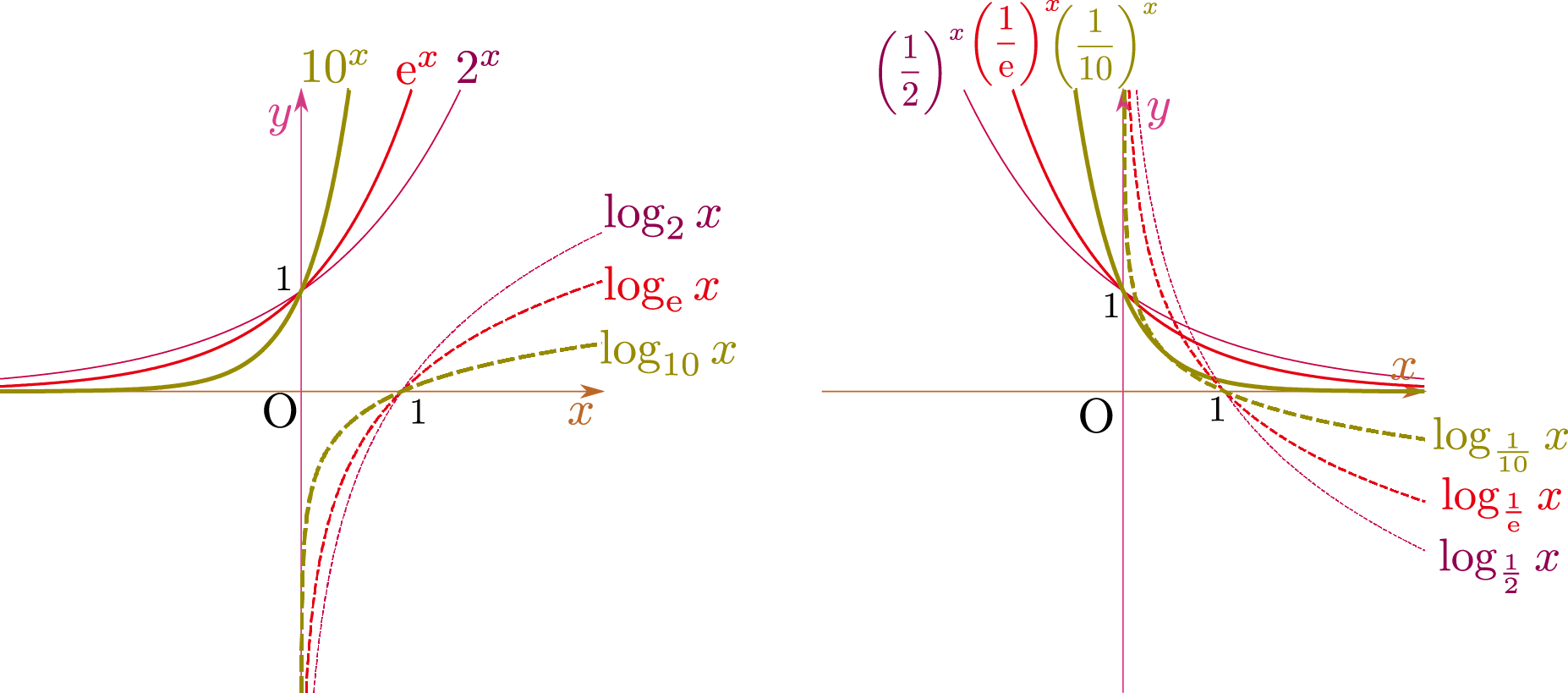
左右を見比べると、指数関数の性質$a^{-\xcol{x}} = \left({1\over a}\right)^{\xcol{x}}$が($\xcol{x}\to-{\xcol{x}}$という変化がグラフ上では左右反転となって)見て取れる。対数関数はこれの逆関数($\xcol{x}$と$\ycol{y}$の立場が入れ替わる)だから、 \begin{equation} \log_a \xcol{x} = -\log_{1\over a}\xcol{x} \end{equation} という関係がわかる(グラフでは上下反転として読み取れる)。
対数関数の公式
指数関数が持っていた「$\E^{\xcol{x}}$の肩の$\xcol{x}$の足算は掛算になる」という性質は、対数においては逆になり、以下の式が成り立つ。
$\log$の真数の$\left\{{掛算\atop 割算}\right\}$は$\log$の$\left\{{足算\atop 引算}\right\}$になる
\begin{equation} \log_a\kakko{x_1x_2}=\log_a{x_1} + \log_a {x_2}\label{logmullogsum} \end{equation} \begin{equation} \log_a\kakko{{x_1\over x_2}}=\log_a{x_1} -\log_a x_2\label{logdivlogdiff} \end{equation}
上の式は、$a^{\log_a(x_1x_2)}=x_1x_2$に$x_1=a^{\log_a x_1}$と$x_2=a^{\log_a x_2}$を代入してみれば、 \begin{equation} a^{\log_a\kakko{x_1x_2}}=a^{\log_a x_1}\times a^{\log_a x_2} \end{equation} となることからわかる。また、$(a^{x_1})^{x_2}=a^{x_1x_2}$となることから逆に、
冪の対数は底の対数の指数倍
\begin{equation} \log_a \xcol{x}^b = b\log_a \xcol{x} \end{equation}
もわかる。
なかなか対数関数($\log$)の「気持ち」がわからない、という人のために$10^\xcol{x}$を例にして説明しよう。
$10^2=100$は0が2桁、$10^3=1000$は0が3桁、$10^4=10000$は0が4桁、と増えていくことを考えると、$\ycol{y}=10^{\xcol{x}}$という関数は
であるとも言える。ここで逆関数である$\xcol{x}=\log_{10}\ycol{y}$は
という関数になる。すなわち、$10\to1,100\to2,1000\to3,\cdots,100000000\to8,\cdots$のような対応関係(言わば、「桁数$-1$を求める関数」である)が、$\xcol{x}=\log_{10}\ycol{y}$という関数が表現する対応関係の「一部」である(実際には$\xcol{x}=\log_{10}\ycol{y}$の$\ycol{y}$には正の実数(負だとどうなるのかは、またこの先で)なら何を入れてもよいから、もっと広い範囲で使える)。
「車の修理代が6桁もかかったわ〜」「え〜っ」のように、数字の大きさを「○桁」で表現することはないだろうか。あれが$\log$の考え方の第一歩だ。
対数関数は「掛算の簡略化」にも使える。たとえば$1000\times 1000=1000000$という計算を「0が3桁ある数字と0が3桁ある数字を掛けたから、0が6桁ある数字になる」という考え方で行うことができる。こう考えると、積の対数関数を対数関数の和に直す式を、 \begin{equation} \log_{10} \underbrace{1000000}_{0が6つ}=\log_{10}\underbrace{1000}_{0が3つ}+\log_{10}\underbrace{1000}_{0が3つ} \end{equation} のように理解できる。
このやり方は$10^n$($n$が整数)の場合しかできないが、そうでない場合に拡張することはできる。
次に、$\ycol{y}=\log_{10}\xcol{x}$の、$\xcol{x}=1$から$\xcol{x}=20$までのグラフを示した。
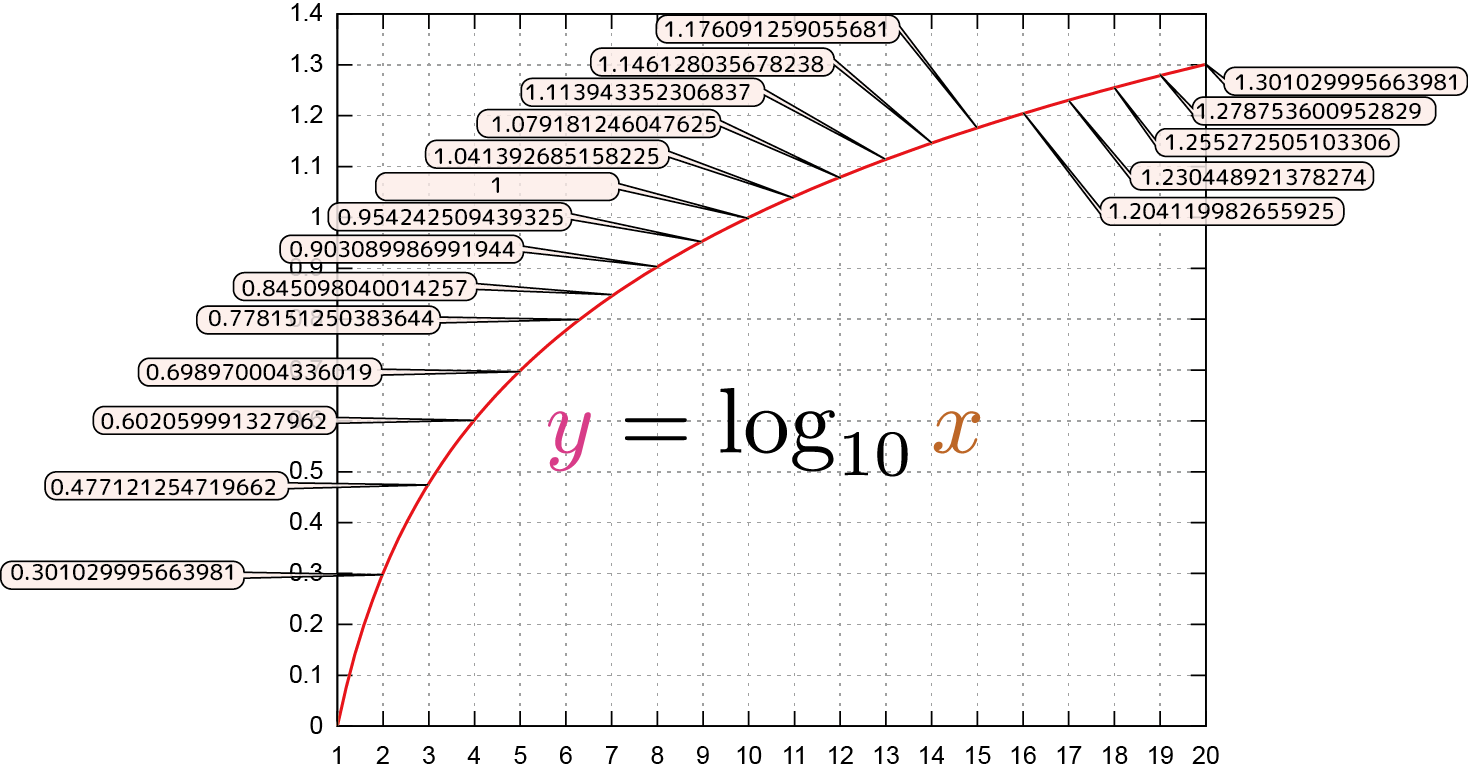
図を見て、たとえば$\log_{10}2+\log_{10}3=\log_{10}6$,$\log_{10}2+\log_{10}5=1$あるいは$\log_{10}9=2\log_{10}3$などのように、「掛算が足算に翻訳されること」を確認しようこんなふうに具体的な数で「対数」というものの勘所をつかむことも重要。この図を見てしばらく「遊ぶ」ぐらいに対数に親しんで欲しい。。
$\log_{10}$の値を前もって調べておくことができると、例えば$5343342\times234234234$という計算を \begin{equation} \log_{10} \left(5343342\times234234234\right) =\underbrace{\log_{10} 5343342}_{6.7278\cdots} + \underbrace{\log_{10} 234234234}_{8.3696\cdots} \fallingdotseq15.0974\label{daitailog} \end{equation} のように、対数を介することで足算を使って実行できる。
逆に$10^{15.0974}$を計算すれば、1251411091802385を得る。この値は、真面目に計算した結果の1251593620370028と比べて、4桁めまで正しい足算の結果を15.0974と小数点以下4桁までしか計算していないので、この程度の精度なのは仕方ない。。今なら電卓なりコンピュータなりで計算するが、昔はいろんな数とその対数の表(「対数表」)が作ってあって、それを使って掛算をしていた対数で目盛を打った物差しのようなもの(計算尺)を使って計算したりもしていた。。
上の計算を大雑把に$5000000\times200000000$として答えを見積もると以下のようになる。
約15.0974という答えは「0が15個より少し大きい」を意味している。
対数関数は「桁数で比較する」という感覚で使われるわけだが、これは概算しているというわけではなく、大きさの変化があまりに大きい物を比較するときに便利な方法であるとも言える。たとえば地球の質量は$5.97\times 10^{24}$ kg、太陽の質量は$1.99\times 10^{30}$ kgである。これを普通の数字で書けば \begin{equation} \begin{array}{rr} 地球の質量:&約5970000000000000000000000 {\rm ~kg} \\ 太陽の質量:&約1990000000000000000000000000000 {\rm ~kg} \end{array} \end{equation} なのだが、こう書かれるよりむしろ$10^?$の形で書いて肩に乗った24や30を見た方が「ああ約$10^6$倍程度違うんだな」が実感しやすい(というより、そういう感覚を持てるようにならないと、大きさの違いが甚だしい量を比較できるようになれない)。

 という交通標識は、道の傾きが0.1であることを示している。
という交通標識は、道の傾きが0.1であることを示している。