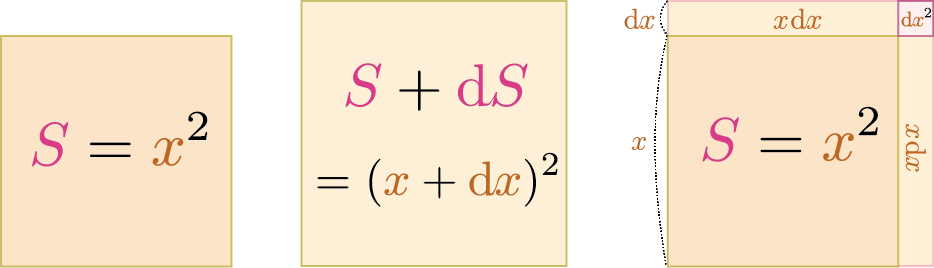微分

$\def\coldr{\rcol{\mathrm dr}}\def\coldvecx{\xcol{\mathrm d\vec x}}\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{~~~~~~~{↓#1}}\def\overbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}\def\kidy{\opcol{\diff y}}\def\ve{\vec{\mathbf e}}\def\colvecx{\xcol{\vec x}}\definecolor{usuopcolor}{RGB}{237,234,203}\def\usuopcol#1{\color{usuopcolor}#1}\def\vgrad#1{{\usuopcol{\overrightarrow{\opcol{\rm grad}~\kuro{#1}}}}}\def\dX{\rcol{\mathrm dX}}\def\dY{\thetacol{\mathrm dY}}$

微分という演算

導関数、微係数

　前回は微分のイメージを図やアニメで見せるところまでだったので、今回は具体的な式を作っておこう。一般の$f\kakko{\xcol{x}}$という関数はある点$x_0$の付近では \begin{equation} f\kakko{\xcol{x}}\simeq a(\xcol{x}-x_0)+b \end{equation} のように直線に近似することができる（$\simeq$は「だいたい等しい」を意味する記号）。定数項$b$は、（両辺に$\xcol{x}=x_0$を代入するとわかるように）実は$f\kakko{x_0}$であり、$a$すなわち傾きは場所によって違うから、「傾きを表す関数」として$f'\kakko{\xcol{x}}$という記号で書くことにしよう。その関数の$\xcol{x}=x_0$での値が$a$である。

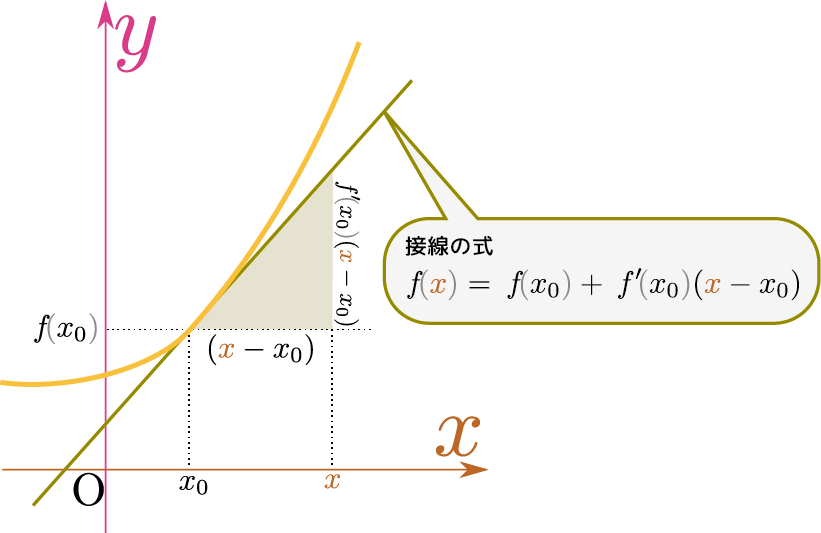
これらを使えば、 \begin{equation} f\kakko{\xcol{x}}\simeq f\kakko{x_0}+ f'\kakko{x_0}(\xcol{x}-x_0) \end{equation} と書いてもよい$f'\kakko{x_0}$は$f\kakko{\xcol{x}}$を$\xcol{x}$で微分してから、$\xcol{x}=x_0$を代入した、という意味である。逆に「$x_0$を代入してから$\xcol{x}$で微分する」とやってはいけない（そんなことをしたら答えは0である）。（右辺の順番を変えたが、別に深い意味はない）。

では、「傾きを表す関数」$f'\kakko{\xcol{x}}$をどう計算しよう？

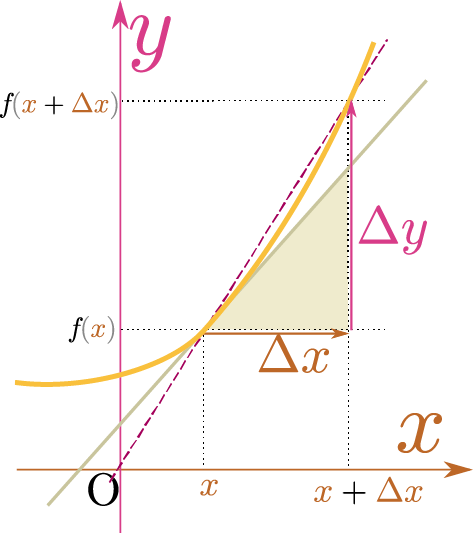
　グラフに示したように、$\ycol{y}$の変化量$\ycol{\Delta y}$は$\ycol{\Delta y}=f\kakko{\xcol{x}+\xcol{\Delta x}}-f\kakko{\xcol{x}}$のような引算で表現できるので、それを$\xcol{\Delta x}$で割った量の$\xcol{\Delta x}\to0$の極限を計算すれば、任意の$\xcol{x}$の点での傾きが計算できる。$\xcol{\Delta x}$が0に近づくとき、図の二つの線が一致していく、と見てよい。

　この任意の$\xcol{x}$の点での傾きもまた$\xcol{x}$の関数となるが、この「新しい関数」を「導関数(derivative)」という名前で呼ぶ。

　「導関数」という言葉は元の関数$f\kakko{\xcol{x}}$から導かれた関数という意味で単に「導く」だといろんな導き方がありそうだが、「導関数」と呼ぶのはこの定義によって導かれた関数のみ。的確に表現された言葉とは言い難いが、広く使われている。、

---

導関数の定義

\begin{equation} \underbrace{ f'\kakko{\xcol{x}}={\mathrm df\over\mathrm dx}\kakko{\xcol{x}}=\ddx f\kakko{\xcol{x}}}_{三通りの書き方}\equiv \lim_{\xcol{\Delta x}\to0}{f\kakko{\xcol{x}+\xcol{\Delta x}}-f\kakko{\xcol{x}}\over \xcol{\Delta x}}\label{bibunteigi} \end{equation} と定義する$\equiv$は「右辺のように定義する」を意味する。。「導関数」は上にも書いたように、三通りの書き方（本によっては別の書き方もある）で表現される。

　関数$\kuro{f\kakko{\xcol{x}}}$からその導関数$\kuro{f'\kakko{\xcol{x}}}$を求める計算（たとえば${f\kakko{\xcol{x}}=\xcol{x}^2}$から$\kuro{f'\kakko{\xcol{x}}=2\xcol{x}}$を導いた計算）を、「微分する」と表現する。同じ内容を、以下のようにも表現できる。 \begin{equation} f\kakko{\xcol{x} + \xcol{\Delta x}}=f\kakko{\xcol{x}}+ f'\kakko{\xcol{x}}\xcol{\Delta x}+\Odr\kakko{(\xcol{\Delta x})^2}\label{bibunteigitwo} \end{equation}

　ここで使った記号$\Odr\kakko{a^n}$（$\Odr$は「オーダー」と読む）は「ランダウの記号」と呼ばれ「計算の主要部ではない部分」を表現するのに使う（上の例では、右辺のうち$f\kakko{\xcol{x}}+ f'\kakko{\xcol{x}}\xcol{\Delta x}$が「主要部」で、左辺のうち「主要部」に含まれなかった部分を$\Odr\kakko{(\xcol{\Delta x})^2}$と書いている）。いわば「その他大勢」扱いされている量である。この「その他大勢」の持つ「重要度」を明記しているのが、$\Odr\kakko{}$の括弧の中身である。

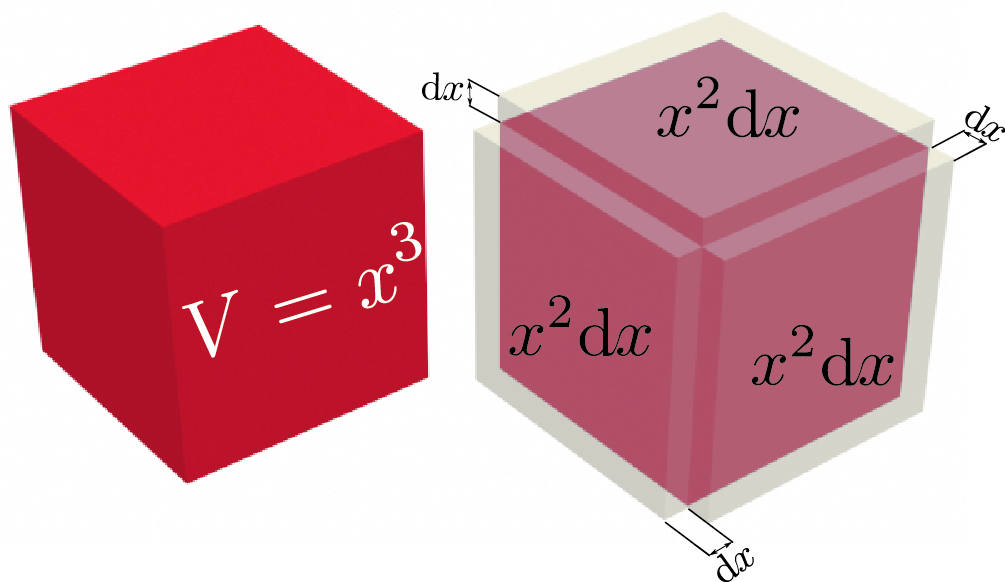
　今ある数が$\xcol{\Delta x}\to0$において0にならないとすると、これは$\Odr\kakko{1}$(おーだーいち)と言う。またある量$A$が$\xcol{\Delta x}$で割ってから$\xcol{\Delta x}\to0$にすると0でない値に収束するとき（${A\over \xcol{\Delta x}}$が0でない値に収束するとき）、この量は$\Odr\kakko{\xcol{\Delta x}}${おーだーでるたえっくす}だ、と言う。同様に、$(\xcol{\Delta x})^n$で割ってから$\xcol{\Delta x}\to0$の極限を取ると0でないとき、$\Odr\kakko{(\xcol{\Delta x})^n}$だ、という。簡単な例を示す。 \begin{equation} (\xcol{x}+\xcol{\Delta x})^3 = \underbrace{\xcol{x}^2+\underbrace{3\xcol{x}^2\xcol{\Delta x} +\underbrace{3\xcol{x}(\xcol{\Delta x})^2 +\underbrace{(\xcol{\Delta x})^3}_{\Odr\kakko{(\xcol{\Delta x})^3}} }_{\Odr\kakko{(\xcol{\Delta x})^2}}}_{\Odr\kakko{\xcol{\Delta x}}}}_{\Odr\kakko{1}} \end{equation}

　$3x(\xcol{\Delta x})^2$だけではなく$3x(\xcol{\Delta x})^2 + (\xcol{\Delta x})^3$全部が$\Odr\kakko{(\xcol{\Delta x})^2}$である（$\Odr\kakko{\xcol{\Delta x}}$も同様）ことに注意しよう。$\Odr\kakko{(\xcol{\Delta x})^n}$のなかには、$n$より大きいオーダーの項$\Odr\kakko{(\xcol{\Delta x})^m}~~(m>n)$が含まれていてもよい。オーダーは「桁」を意味する英語である。

　最後の項$\Odr\kakko{(\xcol{\Delta x})^2}$は、$\xcol{\Delta x}$で割ってから$\xcol{\Delta x}\to 0$の極限を取ると消えてしまう項である（だから、極限を取った後の式には登場しない）。 \begin{equation} \begin{array}{rll} f\kakko{\xcol{x} + \xcol{\Delta x}}=&f\kakko{\xcol{x}}+ f'\kakko{\xcol{x}}\xcol{\Delta x}+\Odr\kakko{(\xcol{\Delta x})^2}&\kokode{移項}\\ f\kakko{\xcol{x} + \xcol{\Delta x}}-f\kakko{\xcol{x}}=& f'\kakko{\xcol{x}}\xcol{\Delta x}+\Odr\kakko{(\xcol{\Delta x})^2}&\kokode{\xcol{\Delta x}で割る}\\ {f\kakko{\xcol{x} + \xcol{\Delta x}}-f\kakko{\xcol{x}}\over \xcol{\Delta x}}=& f'\kakko{\xcol{x}}+\underbrace{{\Odr\kakko{(\xcol{\Delta x})^2}\over \xcol{\Delta x}}}_{極限で消えてしまう項} \end{array} \end{equation}

以上のように、

---

微分の二つの表現

\begin{equation} \begin{array}{lrcl} &f'\kakko{\xcol{x}}&=& \lim_{\xcol{\Delta x}\to0}{f\kakko{\xcol{x}+\xcol{\Delta x}}-f\kakko{\xcol{x}}\over \xcol{\Delta x}}\\[3mm] & f\kakko{\xcol{x} + \xcol{\Delta x}}&=&f\kakko{\xcol{x}}+ f'\kakko{\xcol{x}}\xcol{\Delta x}+\Odr\kakko{(\xcol{\Delta x})^2} \end{array} \end{equation}

---

の二通りの方法で微分という演算を記述できる。二番目の書き方の形では、$f'\kakko{\xcol{x}}$は

---

　$f\kakko{\xcol{x}}$の中の$\xcol{x}$が$\xcol{\Delta x}$変化したときの、$f\kakko{\xcol{x}}$の変化量$\left(f'\kakko{\xcol{x}}\xcol{\Delta x}\right)$の、$\xcol{\Delta x}$の前の係数

---

と言える。よって$f'\kakko{\xcol{x}}$を「微係数(differential coefficient)」（微分係数）とも呼ぶ「導関数」と「微係数」は同じものを指す。「関数から作った、新しい関数（導関数）」と考えるか、「関数を$\xcol{\Delta x}$が小さいところで展開すると出てくる係数（微係数）」と考えるかの違いである。。

$\diff $という記号

　$\xcol{\Delta x}$や$\ycol{\Delta y}$は「変化量」という意味があった。微分を行うときは、$\xcol{\Delta x}$を0に近づける（連動して、$\ycol{\Delta y}$も0に近づく）。このようにここから先の計算ではしばしば、$\xcol{\Delta x}$や$\ycol{\Delta y}$に「変化量」という意味に加えて「0に近づく」という属性が加わる。この「0に近づけていく変化量」という量を表すために、新しい記号として$\coldx$,$\coldy$ を導入しよう。

$\Delta$の替りに$\diff $という記号を使って後で$\to0$という極限を取ることが約束されている変化量を示す。$\coldx$ とか$\coldy$ のように$\diff $のついた量は、すべて「微小変化」を表現する量である。

　$\coldx$ や$\coldy$ を「微小変化」と呼ぶが、この呼び方は少し説明が不足していて、単に「微小」ではなく「後で0になる極限を取ることが運命づけられている」という点が重要である。

　この「運命」があることで実際の計算上何が違うかというと、今考えている量より次数の高い項は無視してよくなる点である。1次までを考えているならば「$\coldx$や$\coldy$の二次以上の量（$\Odr\kakko{\coldx^2}$や$\Odr\kakko{\coldy^2}$）を無視する」というルールで計算していけばよい。

　$\diff $を使った書き方では、$f\kakko{\xcol{x} + \xcol{\Delta x}}=f\kakko{\xcol{x}}+ f'\kakko{\xcol{x}}\xcol{\Delta x}+\Odr\kakko{(\xcol{\Delta x})^2}$は

---

$\diff $を使って書いた微分の定義

\begin{equation} f\kakko{\xcol{x} + \coldx}=f\kakko{\xcol{x}}+ f'\kakko{\xcol{x}}\coldx \end{equation}

---

となる。$\coldx^2$にあたる項は書かなくてよい。いろんな関数の微分を計算するときや、実際に自然科学で現れる量の微小変化を考えるときも、$ f\kakko{\xcol{x} + \coldx}=f\kakko{\xcol{x}}+ f'\kakko{\xcol{x}}\coldx$という書き方は便利である。

　「微小」とか「無限小」とかいう考え方がどうにも納得しがたい、という人は以下のように考えると、「無限小」という考え抜きで導関数を定義できる。

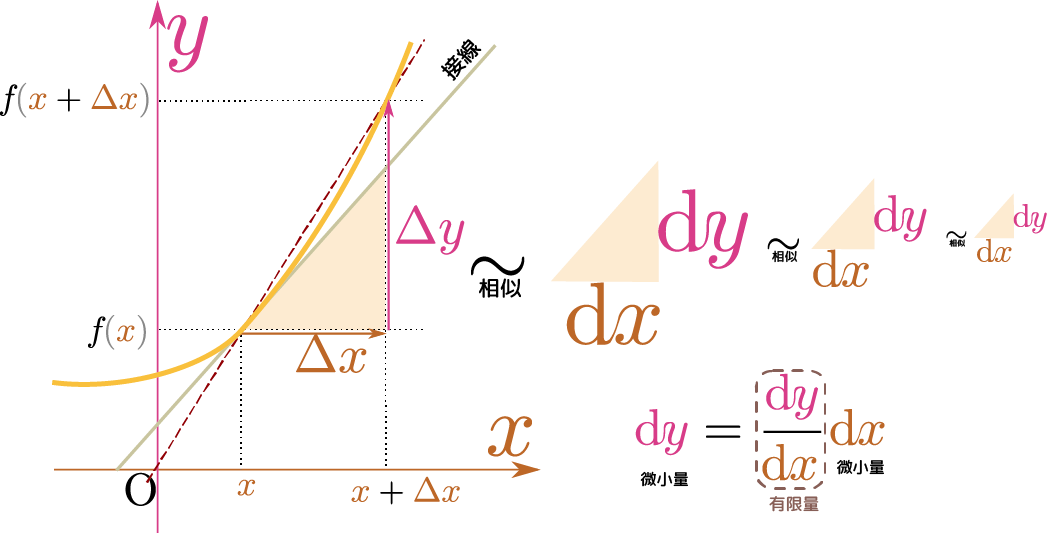
　上の図にも示したように、$\coldx$ や$\coldy$ はあくまで、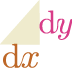のような「接線と同じ傾きを斜辺とした直角三角形」の底辺と高さだと考える（この考え方なら微小である必要はない）。そして、$\coldx$ や$\coldy$ そのものの大きさは重要ではなく、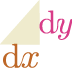がどんな直角三角形か、あるいは「$\coldx$ と$\coldy$ の比」が重要であって、$\coldx$ や$\coldy$ そのものは大きさを考えてはいけない（考えても意味はない）どうして比だけが重要になるかというと、微小な（狭い）範囲を考えていて、その範囲では関数のグラフが直線だと思っていいからである、とも言える。。$\coldx$ と$\coldy$ は、それぞれ一つだけでは意味がなく、「$\coldx$ と$\coldy$ の二つで向きを表現する量」なのである。

　こう考えてもよい。どんな関数でも（微分可能な関数なら）上のグラフのように接線を引くことができる。本来、今考えている$\xcol{x}$と$\ycol{y}$はもともとのグラフである曲線に沿って変化する量だが、関数を1次式に近似して、接線の上を$\xcol{x},\ycol{y}$が移動すると考える。そのときの$\xcol{x},\ycol{y}$の変化量が$\coldx$や$\coldy$なのである。接線は直線だから$\coldx$と$\coldy$の関係は常に1次式で、2次以上のものは出てこない。

　${\coldy\over \coldx}$は普通の数（大きさを考える意味がある）だし、$\coldy=a\coldx$と書いたときの$a$も普通の数である。だから${\coldy\over \coldx}=2$や$\coldy = 0.7\coldx$は意味のある式である（どんな意味があるか、絵が描けるだろうか？）。

しかし、$\coldx=1$とか$\coldy=0.02$などには全く意味がない$=0$だけは、「変化しない」ということを「$\coldx=0$」と表すこともあるが、本来はあまりよい使い方ではない。。$\coldy$ や$\coldx$ は、ペアになって接線の向きを表現する量であって$\coldx$のみの大小を云々できない。

　新しい記号を使えば、 \begin{equation} {\coldy\over\coldx}=\lim_{\xcol{\Delta x}\to0}{\ycol{\Delta y}\over \xcol{\Delta x}} \end{equation} が接線の傾きとなる。こうして「傾き」を$\xcol{x}$の関数として表現する方法を我々は得た。

　これが導関数（もしくは微係数）を${\dy\over \dx}\kakko{\xcol{x}}$のように書く理由である。

微分演算の簡単な例

　$\coldx$を使って微分の計算を行ってみよう。この記号を使えば、微分の定義式は以下のようになる。 \begin{equation} f\kakko{\xcol{x}+\coldx}=f\kakko{\xcol{x}}+f'\kakko{\xcol{x}}\coldx \end{equation}

　前に行った$f\kakko{\xcol{x}}=\xcol{x}^2$の微分を例としよう。まず、$\ycol{\Delta y}=2\xcol{x\Delta x}+(\xcol{\Delta x})^2$を \begin{equation} \coldy=2\xcol{x}\coldx+(\coldx)^2\label{twoxdxdxtwo} \end{equation} と書きなおす。この式の$\coldx\to0,\coldy\to0$の極限を考えると \begin{equation} \underbrace{ \coldy}_{\to0} = \underbrace{2\xcol{x}\coldx}_{\to0} + \underbrace{(\coldx)^2}_{\to0} \end{equation} となって$0=0$という「当たり前すぎてつまんない（trivialな）式」が出る。これでは何の情報も引き出せない。$\coldy$と$\coldx$の比のみが重要なのだから、まず両辺を$\coldx$で割って \begin{equation} {\coldy\over\coldx} = 2\xcol{x} + \coldx\label{A3} \end{equation} とした後に$\coldx\to0$という極限を取ることで、以下の式を得るここで左辺がいわば「$0\div0$を計算している」部分である。しかし、${\coldy\over\coldx}$ は「$\coldy$ と $\coldx$ の割合」を意味しているのであり、その量は$\coldx \to0,\coldy\to0$となっても0に近づかない。。 \begin{equation} {\coldy\over\coldx} = 2\xcol{x} \label{A5} \end{equation}

　「${\coldy\over \coldx}$は割算ではない！」と注意されることが多いものだから、「こんな計算やっていいの？」と悩む人が多い。${\coldy\over \coldx}=a$と$\coldy=a\coldx$は、どちらも「比」だけを問題にしている式である。「単純な割算ではない」が、「${\coldy\over \coldx}=a$から$\coldy=a\coldx$と結論してよい」という性質に関しては割算と共通である。単純な割算ではないことを忘れてはいけないが、だからと言って「割算と同じ計算をやることは一切禁じられている」わけでもない。

　この式の段階で、「$\coldx$というのは0にする極限を取られることを運命づけられている量であることを考えると、右辺第二項の$(\coldx)^2$をこれ以上計算する必要はない」と考えて \begin{equation} \coldy= 2\xcol{x}\coldx+\underbrace{(\coldx)^2}_{無視}\label{whykesi} \end{equation} として${\coldy\over\coldx}=2\xcol{x}$を出してもよい。というより慣れてきたらそうするべきである。

　$2\xcol{x}\coldx$と$(\coldx)^2$を比較して、「$(\coldx)^2$の方が速く0になる」という判断で消す。具体的には$\coldx$の次数を考える。$2\xcol{x}\coldx$は$\coldx$の1次、$(\coldx)^2$は$\coldx$の2次である。$\coldx$の次数が1次の量と2次の量があれば、1次の量）だけが最後に残り、2次の量は消していい。

　あくまで「小さい物＋もっと小さい物」という形になっているときに「もっと小さい物」の方が消せる、ということに注意しようこういうのはお金の話で考えるのが理解しやすいようである。たとえば、国家予算の話をしているときには100円の差なんて無視していいが、今日の昼御飯何を食べるか考えているときには、100円の差は大きい。。このようにして消される量は「高次の微小量」と呼ばれる。このようなときも「$\coldx$と$(\coldx)^2$は\reftext{whatisorder}{オーダー}が違う」という言い方をする。$2\xcol{x}\coldx$は「\coldx の1次のオーダー」、$(\coldx)^2$は「\coldx の2次のオーダー」である。今の場合オーダーが高いほど小さいので、次数が一番低いオーダー（今は1次）の量だけを考えておけばよい。2次が一番低いオーダーのときは2次を残して3次以上を無視する。何がなんでも2次を無視するのでははなく、「考えている中でもっとも低いオーダーのみを残す」と考える。

　次に図解で考えよう。一辺$\xcol{x}$の正方形の面積${S}$は${S}=\xcol{x}^2$という式で表現できる$\ycol{y}$ではなく${S}$を使ったのはこの式に「面積」という意味があるから。どんな文字を使うかは本質とは関係ない。。

　上図から面積の導関数が$\opcol{\diff \kuro{S\kakko{\xcol{x}}}\over \kidx}=2\xcol{x}$だと理解できる。「縦」の変化による面積変化$\xcol{x}\coldx$と「横」の変化による面積変化$\xcol{x}\coldx$の和が微分$2\xcol{x}\coldx$となっている。$\coldx^2$の部分は無視されている。

　慣れてきたら、以下のように考えよう。$\ycol{y}=\xcol{x}^2$の両辺を微小変化させると \begin{equation} \ycol{y}+\coldy = (\xcol{x}+\coldx)(\xcol{x}+\coldx) \end{equation} になる。そして「あ、この中には$\xcol{x}\coldx$が2個あるな」と考えれば、右辺は$\xcol{x}^2+2\xcol{x}\coldx$となる。慣れてくると、「$\coldx\times\coldx$なんて考えなくていい」とさっと判断できるようになるのである。

　次に$\ycol{y}=\xcol{x}^3$を考えよう。今度はまず図で考えることにして、右の図のように立方体が大きくなるところを想像するとよい。体積が$\xcol{x}^2\coldx$増える場所が３箇所あるから、$3\xcol{x}^2\coldx$という式が微分の結果として出てきそうである。他に$\xcol{x}\coldx^2$が三つと$\coldx^3$が一つあるが、高次の微小量として無視できる。このことを数式で確認しよう。

\begin{equation} \ycol{y}+\coldy = (\xcol{x}+\coldx)(\xcol{x}+\coldx)(\xcol{x}+\coldx) \end{equation} として、「この中には$\xcol{x}^2\coldx$が三つある」ことだけ判断して、 \begin{equation} \underbrace{\ycol{y}}_{相殺→}+\coldy =\underbrace{\xcol{x}^3}_{←相殺} +3\xcol{x}^2\coldx\underbrace{+\Odr\kakko{{\coldx^2}}}_{省略可} \end{equation} とすればよい。「省略可」の部分は「今は$\coldx$ の1次までしか計算しない」を最初から明示しておくならば、書かなくてもよい。

　あるいは、$\ycol{y}=\xcol{x}\times\xcol{x}\times \xcol{x}$の微小変化を、「最初の$\xcol{x}$が変化した場合」「真ん中の$\xcol{x}$が変化した場合」「最後の$\xcol{x}$が変化した場合」の三つにわけて考えたと思ってもよい。

　こうして$\ycol{y}=\xcol{x}^3$ならば${\coldy\over \coldx}= 3\xcol{x}^2$あるいは$\coldy=3\xcol{x}^2\coldx$という式を得た。右に描いたグラフが$\ycol{y}=\xcol{x}^3$のグラフと、その微分（傾き）であるところの$\rcol{y'}=3\xcol{x}^2$のグラフである。確かに下のグラフが上のグラフの「傾き」を表現していることがわかるだろう。

冪の微分

　$\xcol{x}^2,\xcol{x}^3$の場合をここまで考えたが、$\xcol{x}^n$の微分も同様に \begin{equation} \ycol{y}+\coldy=\underbrace{(\xcol{x}+\coldx)(\xcol{x}+\coldx)(\xcol{x}+\coldx)(\xcol{x}+\coldx)\cdots }_{n個} \end{equation} の中にある$\coldx$の1次は$n$個の$\xcol{x}^{n-1}\coldx$であろうと考えるか、もしくは \begin{equation} \underbrace{\ycol{y}}_{これが変化すると}=\underbrace{\xcol{x}\times\xcol{x}\times\xcol{x}\times\xcol{x}\times\xcol{x}\times\xcol{x}\times\xcol{x}\times\cdots }_{このうち一つが\coldx 変化したものが全部でn種類出てくる} \end{equation} と考える（二つ以上の$\xcol{x}$が$\coldx$ に変化したものは、$\Odr\kakko{\coldx^2}$なので無視）と、以下がわかる。 \begin{equation} \coldy = n\xcol{x}^{n-1}\coldx~~~すなわち、{\coldy\over \coldx}= n\xcol{x}^{n-1}\label{nxnhikuone} \end{equation}

　上の式は$n$が自然数なら正しい。では、指数が負の整数ならどうなるだろうか。まず$n=-1$の場合を考える。$\ycol{y}={1\over \xcol{x}}$を$\xcol{x}\ycol{y}=1$と書きなおしてから、この式の両辺の微小変化を \begin{equation} \begin{array}{rll} (\xcol{x}+\coldx)(\ycol{y}+\coldy)=&1\\ \underbrace{\xcol{x}\ycol{y}}_{=1で、\atop 右辺と相殺}+\underbrace{\ycol{y}\coldx}_{{右辺に\atop 移項}→}+\xcol{x}\coldy+\underbrace{\coldx\coldy}_{高次の微小量} =&1\\ \end{array}\label{diffoneoverx} \end{equation} のように計算して、$\xcol{x}\coldy = -\ycol{y}\coldx$から${\coldy\over \coldx}=-{\ycol{y}\over \xcol{x}}$、さらに$\ycol{y}={1\over \xcol{x}}$だから${\coldy\over \coldx}=-{1\over \xcol{x}^2}$を得る。

　$n$が一般の負の整数である場合は、$\ycol{y}=\xcol{x}^{-n}$をまず、$\xcol{x}^n \ycol{y}=1$に直してから、 \begin{equation} \begin{array}{rll} \underbrace{(\xcol{x}+\coldx)(\xcol{x}+\coldx)(\xcol{x}+\coldx)(\xcol{x}+\coldx)\cdots }_{n個}\times(\ycol{y}+\coldy)=&1\\ \underbrace{\left(\xcol{x}^n + n\xcol{x}^{n-1}\coldx\right)}_{\Odr\kakko{\coldx^2}は消した}\times(\ycol{y}+\coldy)=&1\\[5mm] \underbrace{\xcol{x}^n \ycol{y}}_{=1で、\atop 右辺と相殺} + \underbrace{n\xcol{x}^{n-1}\coldx\ycol{y}}_{{右辺に\atop 移項}→} + \xcol{x}^n \coldy =&\underbrace{1}_{左辺の\xcol{x}^n\ycol{y}\atop と相殺}\label{fubekibibunone} \end{array} \end{equation} のように微小変化を計算し、 \begin{equation} \begin{array}{rll} \xcol{x}^n \coldy =&-n\xcol{x}^{n-1}\coldx \xcol{x}^{-n}\\ \coldy =& -n \xcol{x}^{-n-1}\coldx\\ {\coldy\over \coldx} =& -n \xcol{x}^{-n-1} \end{array} \end{equation} となる慣れてきたら、「$\xcol{x}^n \ycol{y}=1$の両辺を微分する」の一言で$n\xcol{x}^{n-1}\coldx \ycol{y}+ \xcol{x}^n \coldy =0$を出してよい。。結果を見ると、${\coldy\over \coldx}= n\xcol{x}^{n-1}$の$n$を$-n$に置き換えた式になっているここで「じゃあ、証明しなくてもよかったんだ」と早とちりする人が時々いるが、前の式を出したときには$n$は自然数だとしている。$n$が負の整数である場合については別に証明する必要があるので、この証明はやらなくてはいけない。。

　指数が整数でない場合を考えよう。$\ycol{y}=\xcol{x}^{1\over n}$（$n$は自然数）をまず$\ycol{y}^n = \xcol{x}$になおしてから、 \begin{equation} \underbrace{(\ycol{y}+\coldy)(\ycol{y}+\coldy)(\ycol{y}+\coldy)(\ycol{y}+\coldy)\cdots }_{n個}= \xcol{x}+\coldx \end{equation} とすれば（これまで同様、1次のオーダーを取り出すことで）こちらも慣れてくれば、$\ycol{y}^n = \xcol{x}$からすぐに$n \ycol{y}^{n-1}\coldy = \coldx$が出せるだろう。、 \begin{equation} \begin{array}{rl} n \ycol{y}^{n-1}\coldy =& \coldx\\ {\coldy\over \coldx} =& {1\over n \ycol{y}^{n-1}}={1\over n}\xcol{x}^{{1\over n}-1}\\ \end{array} \end{equation} がわかる（$\ycol{y}^{n-1}=\xcol{x}^{{1\over n}(n-1)}=\xcol{x}^{1-{1\over n}}$に注意）。一例として$\ycol{y}=\sqrt{\xcol{x}}=\xcol{x}^{1\over 2}$の微分は \begin{equation} {\coldy\over \coldx}={1\over 2}\xcol{x}^{-{1\over 2}}={1\over 2\sqrt{\xcol{x}}}\label{diffsqrtx} \end{equation} である。ここで$\xcol{x}=0$の点では右辺は定義されないから、「$\xcol{x}=0$では$\sqrt{\xcol{x}}$は微分不可能」ということになる。

　同様に、$\ycol{y}=\xcol{x}^{m\over n}$も$\ycol{y}^n=\xcol{x}^m$としてから \begin{equation} \begin{array}{rl} \underbrace{(\ycol{y}+\coldy)(\ycol{y}+\coldy)(\ycol{y}+\coldy)\cdots }_{n個}=& \underbrace{(\xcol{x}+\coldx)(\xcol{x}+\coldx)(\xcol{x}+\coldx)(\xcol{x}+\coldx)\cdots }_{m個}\\[3mm] \underbrace{\ycol{y}^n}_{相殺→}+n\ycol{y}^{n-1}\coldy+\cdots =& \underbrace{\xcol{x}^m}_{←相殺}+ m \xcol{x}^{m-1}\coldx+\cdots\\ {\coldy \over \coldx}=& {m\xcol{x}^{m-1}\over n\ycol{y}^{n-1}}={m\xcol{x}^{m-1}\over n\xcol{x}^{{m\over n}(n-1)}}={m\xcol{x}^{m-1}\over n\xcol{x}^{m-{m\over n}}} ={m\over n} \xcol{x}^{{m\over n}-1} \end{array} \end{equation} のように考えれば、 \begin{equation} 有理数\alpha={m\over n}に対して、~\ycol{y}=\xcol{x}^\alpha~ の微分は ~{\coldy\over \coldx}= \alpha \xcol{x}^{\alpha-1} \end{equation} がわかる。ここまでくれば、「無理数に対しても極限操作で定義すればよい（たとえば$\xcol{x}^{\pi}$は$\xcol{x}^3\to\xcol{x}^{3.1}\to\xcol{x}^{3.14}\to\cdots$）」とわかる科学で必要な数は測定等で入る誤差を不可避に含んでいることを思えば、「ある無理数に十分近い有理数${m\over n}$に対する値が用意できれば問題はない」と開き直ってもよいだろう。ので、$\alpha$は任意の実数でよい。微分により$\xcol{x}$の冪が1ずつ下がる。例外は定数（すなわち$\xcol{x}^0$）で、このときだけは$(定数)\times \xcol{x}^{-1}$とはならず、0となるでは微分すると$\xcol{x}^{-1}={1\over\xcol{x}}$になる関数はないのかというと、ある。多項式の形では書けないだけである。

。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。