微分（続き）

$\def\coldr{\rcol{\mathrm dr}}\def\coldvecx{\xcol{\mathrm d\vec x}}\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{~~~~~~~{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}\def\kidy{\opcol{\diff y}}\def\ve{\vec{\mathbf e}}\def\colvecx{\xcol{\vec x}}\definecolor{usuopcolor}{RGB}{237,234,203}\def\usuopcol#1{\color{usuopcolor}#1}\def\vgrad#1{{\usuopcol{\overrightarrow{\opcol{\rm grad}~\kuro{#1}}}}}\def\dX{\rcol{\mathrm dX}}\def\dY{\thetacol{\mathrm dY}}\def\opdf{\opcol{\mathrm df}}\def\coldf{\tcol{\mathrm df}}$

微分の性質と、簡単な関数の微分

微分という演算の持つ性質

---

微分の性質

1. 線形性：~$\alpha,\beta$は定数として、$\ddx \left(\alpha f\kakko{\xcol{x}}+\beta g\kakko{\xcol{x}}\right)=\alpha \ddx f\kakko{\xcol{x}}+\beta\ddx g\kakko{\xcol{x}}$
   または
   $(\alpha f\kakko{\xcol{x}}+\beta g\kakko{\xcol{x}})'=\alpha f'\kakko{\xcol{x}}+\beta g'\kakko{\xcol{x}}$
2. ライプニッツ則：$\ddx \left(f\kakko{\xcol{x}}g\kakko{\xcol{x}}\right)=\left(\ddx f\kakko{\xcol{x}}\right)g\kakko{\xcol{x}}+f\kakko{\xcol{x}}\ddx g\kakko{\xcol{x}}$
   または
   $(f\kakko{\xcol{x}}g\kakko{\xcol{x}})'=f'\kakko{\xcol{x}}g\kakko{\xcol{x}}+f\kakko{\xcol{x}}g'\kakko{\xcol{x}}$
3. 合成関数の微分：~${\ddx}g\kakko{f\kakko{\xcol{x}}}=\left(\ddx f\kakko{\xcol{x}}\right)\left(\opcol{\diff \over \opdf}g\kakko{f\kakko{\xcol{x}}}\right)$
   または
   $\left(g\kakko{f\kakko{\xcol{x}}}\right)'=f'\kakko{\xcol{x}}g'(f\kakko{\xcol{x}})$

---

　以上がよく使う、微分という演算の性質である。「微分」という演算の意味がわかっていれば、どの性質も少し考えれば納得できるはずである。

「線形性」「線形」と書いてある本と「線型」と書いてある本があるが、意味は同じ。という言葉は、以下の二つの性質を合わせ持っていることを表す。

---

「線形性」の意味するところ

• 足算と微分の順番はどちらが先でもよい。 $\left(\ddx (f\kakko{\xcol{x}}+g\kakko{\xcol{x}})=\ddx f\kakko{\xcol{x}}+\ddx g\kakko{\xcol{x}}\right)$
• 定数を掛けるという計算と微分の順番はどちらが先でもよい。 $\left(\ddx (\alpha f\kakko{\xcol{x}})=\alpha\ddx f\kakko{\xcol{x}}\right)$

---

　確認するには、$\alpha f\kakko{\xcol{x}}+\beta g\kakko{\xcol{x}}$を微小変化させてみればよい（ここ以後しばらくの計算では$\Odr\kakko{(\coldx)^2}$には興味がないので省略する）。 \begin{equation} \begin{array}{rl} \alpha f\kakko{\xcol{x}+\coldx}+\beta g\kakko{\xcol{x}+\coldx} =& \alpha \underbrace{(f\kakko{\xcol{x}}+f'\kakko{\xcol{x}}\coldx)}_{\small f\kakko{\xcol{x}+{\coldx}}}+\beta \underbrace{(g\kakko{\xcol{x}}+g'\kakko{\xcol{x}}\coldx)}_{g\kakko{\xcol{x}+{\coldx}}} \\ =&\alpha f\kakko{\xcol{x}}+\beta g\kakko{\xcol{x}} +\underbrace{ (\alpha f'\kakko{\xcol{x}}+\beta g'\kakko{\xcol{x}})}_{(\alpha f\kakko{\xcol{x}}+\beta g\kakko{\xcol{x}})'}\coldx \end{array} \end{equation} となって線形性が確認できる。この式をあえて図で表現しておくと以下のようになる。

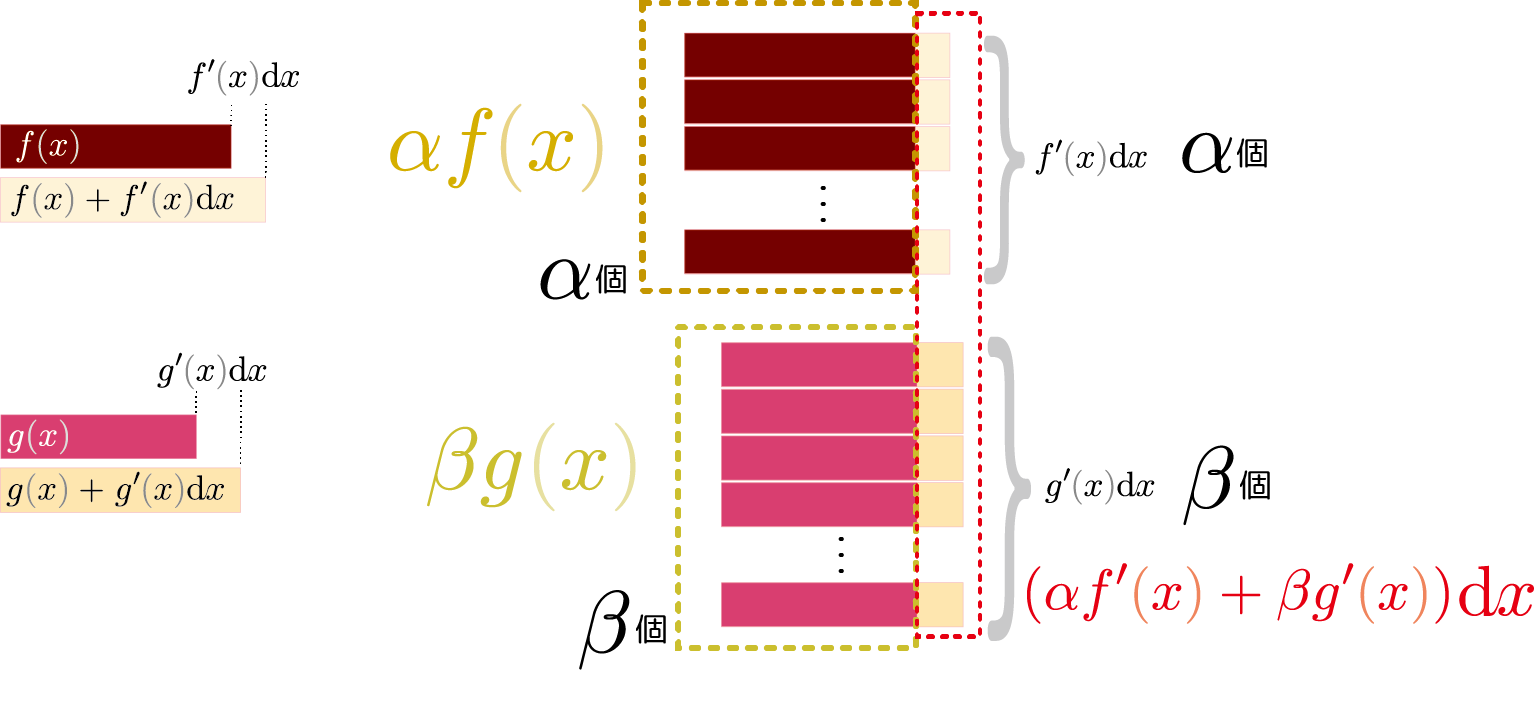
　この線形性のおかげで、 \begin{equation} \ddx \left( a \xcol{x}^\alpha + b \xcol{x}^\beta + c\xcol{x}^\gamma+\cdots\right) = a\alpha \xcol{x}^{\alpha-1}+ b\beta \xcol{x}^{\beta-1}+ c\gamma \xcol{x}^{\gamma-1}+\cdots \end{equation} のように冪の和の微分も「各項ごとに微分する」ことで簡単にできる。

　次の「ライプニッツ則（Leibniz rule）」は具体的には、 \begin{equation} \begin{array}{rl} f\kakko{\xcol{x}+\coldx}g\kakko{\xcol{x}+\coldx} =&\underbrace{(f\kakko{\xcol{x}}+f'\kakko{\xcol{x}}\coldx)}_{\small f\kakko{\xcol{x}+\coldx}}\underbrace{(g\kakko{\xcol{x}}+g'\kakko{\xcol{x}}\coldx)}_{\small g\kakko{\xcol{x}+\coldx}}\\ =&f\kakko{\xcol{x}}g\kakko{\xcol{x}}+f'\kakko{\xcol{x}}g\kakko{\xcol{x}}\coldx+f\kakko{\xcol{x}}g'\kakko{\xcol{x}}\coldx\\[3mm] =&f\kakko{\xcol{x}}g\kakko{\xcol{x}}+\underbrace{(f'\kakko{\xcol{x}}g\kakko{\xcol{x}}+f\kakko{\xcol{x}}g'\kakko{\xcol{x}})}_{(f\kakko{\xcol{x}}g\kakko{\xcol{x}})'}\coldx\\ \end{array} \end{equation} という計算をやると、右辺の$\coldx$の1次のオーダーの係数（微係数）が$f'\kakko{\xcol{x}}g\kakko{\xcol{x}}+f\kakko{\xcol{x}}g'\kakko{\xcol{x}}$であることがわかる。下の図はこの微分演算で行われている微小変化のイメージである。

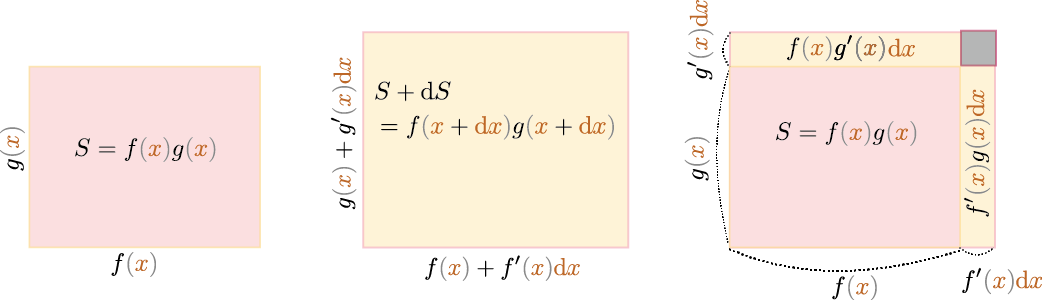
　最後に合成関数の微分（このルールは「連鎖律（chain rule）」とも呼ばれる）を数式で表現しておこう。$g\kakko{f\kakko{\xcol{x}}}$という合成関数を考えて、その独立変数$\xcol{x}$を$\xcol{x}+\coldx$と微小変化させると、 \begin{equation} f\kakko{\xcol{x}+\coldx}= f\kakko{\xcol{x}}+ \underbrace{f'\kakko{\xcol{x}}\coldx}_{\diff (f\kakko{\xcol{x}})}\label{fdashfx} \end{equation} のように$f\kakko{\xcol{x}}$が変化する。ここで$\diff (f\kakko{\xcol{x}})=f'\kakko{\xcol{x}}\coldx$という記号を使った。$\diff(なんとか)$のように$\diff $をつけることで(なんとか)の微小変化という意味を持たせるこれをさらに省略して$\mathrm df\kakko{\xcol{x}}$、さらに$\kakko{\xcol{x}}$も省略して$\mathrm df$とだけ書いたりもする。。ライプニッツの記号では、$\diff (f\kakko{\xcol{x}})={\mathrm df\over \mathrm dx}\kakko{\xcol{x}}\coldx$と書けて、「$\mathrm dx$を約分している」というイメージで捉えることができる。

　$f\kakko{\xcol{x}}$の$\xcol{x}$が微小変化すると、$g\kakko{f\kakko{\xcol{x}}}$は\begin{equation} g\kakko{f\kakko{\xcol{x}+\coldx}}= g\kakko{f\kakko{\xcol{x}}+f'\kakko{\xcol{x}}\coldx}\label{fdash} \end{equation}と微小変化する。上にも書いたように、$f'\kakko{\xcol{x}}\coldx$の部分を$\diff(f\kakko{\xcol{x}})$と考えれば、上の式の$f\kakko{\xcol{x}}$の部分を$\tcol{f}$という変数に置き換え、$\tcol{f}$が\coldf すなわち$\diff (f\kakko{\xcol{x}})$だけ変化していると解釈して \begin{equation} g\kakko{\tcol{f}+\coldf}= g\kakko{\tcol{f}}+g'\kakko{\tcol{f}}\coldf \end{equation} と書く。この$g'(\tcol{f})$はもちろん$g\kakko{\tcol{f}}$を$\tcol{f}$で微分した結果である。$\tcol{f}$を元の$f\kakko{\xcol{x}}$に戻すと \begin{equation} g\kakko{f\kakko{\xcol{x}}+\diff (f\kakko{\xcol{x}})}= g\kakko{f\kakko{\xcol{x}}}+g'\kakko{f\kakko{\xcol{x}}}\underbrace{f'\kakko{\xcol{x}}\coldx}_{\diff (f\kakko{\xcol{x}})} \end{equation} なので、$g\kakko{f\kakko{\xcol{x}}}$の導関数が$g'\kakko{f\kakko{\xcol{x}}}f'\kakko{\xcol{x}}$だとわかる。

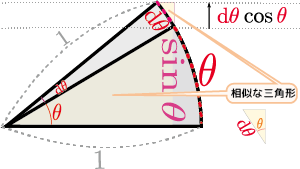
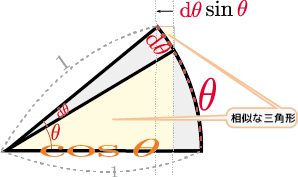
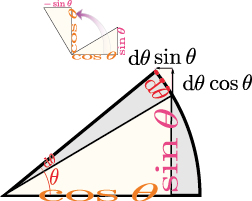
　$\xcol{x}\to\ycol{y}\to\zcol{z}$（$\ycol{y}=f\kakko{\xcol{x}},\zcol{z}=g\kakko{\ycol{y}}$）という関係がある時、$\xcol{x}$を微小変化させた時にそれに応じて$\ycol{y}$が、さらに連鎖して$\zcol{z}$が変化する様子を前に書いた図同様、立体図で表現しよう。

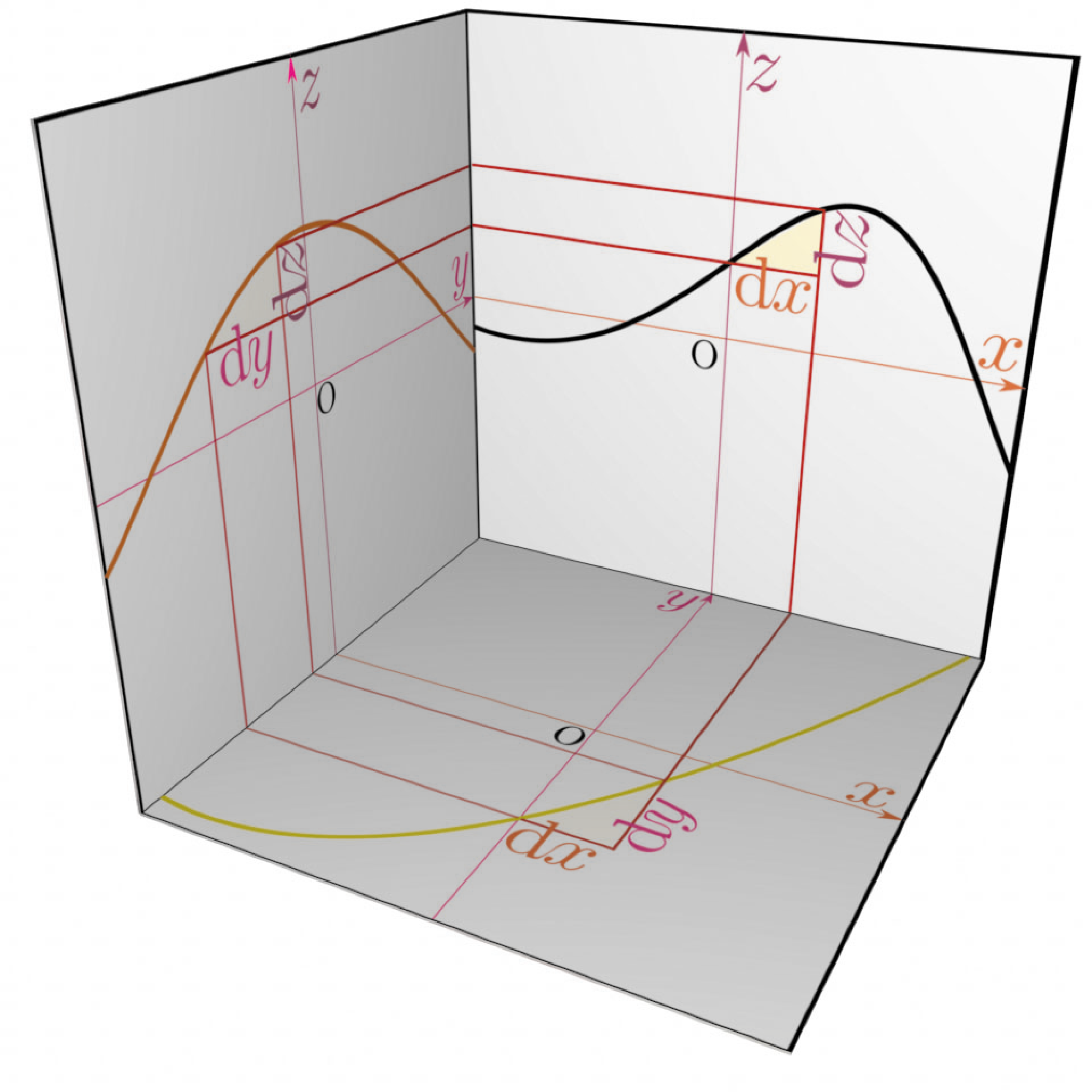
　上の図に${\mathrm dy\over \mathrm dx}\kakko{\xcol{x}},{\mathrm dz\over \mathrm dy}\kakko{\ycol{y}},{\mathrm dz\over \mathrm dx}\kakko{\xcol{x}}$の三つの導関数に対応する三角形（この三角形の傾きが導関数の値）が描かれている。導関数は$\coldx,\coldy,\coldz$という三つの微小量の比でここでも計算しているのは微小変化の「比」だけであって、微小変化そのものではない。計算されるものだから、 \begin{equation} \begin{array}{c} {\mathrm dz\over \mathrm dy}\kakko{\ycol{y}} {\mathrm dy\over \mathrm dx}\kakko{\xcol{x}}={\mathrm dz\over \mathrm dx}\kakko{\xcol{x}}\\ ただし、\ycol{y}=f\kakko{\xcol{x}} \end{array} \end{equation} が成立する。この計算は、${\coldz\over {\coldy}}{{\coldy}\over \coldx}={\coldz\over \coldx}$という「約分」を行った、と解釈できる。

　例として$f\kakko{\xcol{x}}=(\xcol{x}^2+\xcol{x})^3$の微分をしてみよう。これを$f\kakko{\ycol{y}}=\ycol{y}^3,\ycol{y}=g\kakko{\xcol{x}}=\xcol{x}^2+\xcol{x}$として、$f\kakko{\xcol{x}}=f\kakko{g\kakko{\xcol{x}}}$と考えてから微分すると、 \begin{equation} \ddx f\kakko{\xcol{x}}=\underbrace{ \ddx g\kakko{\xcol{x}}}_{(2\xcol{x}+1)} \underbrace{ \opcol{\diff \over \kidy}f\kakko{\ycol{y}}}_{3\ycol{y}^2} = 3(2\xcol{x}+1)\underbrace{(\xcol{x}^2+\xcol{x})^2}_{\ycol{y}^2} \end{equation} となる。慣れてきたら$\ycol{y}$を導入するのも省略して、 \begin{equation} \underbrace{ \diff \left((\xcol{x}^2+\xcol{x})^3\right)}_{\fbox{？}^3の微分} =\underbrace{3 (\xcol{x}^2+\xcol{x})^2}_{3\fbox{？}^2} \times\underbrace{ \diff (\xcol{x}^2+\xcol{x}) }_{\fbox{？}の微分}=3(2\xcol{x}+1)(\xcol{x}^2+\xcol{x})^2\coldx \end{equation} のように計算してよい。

　$\sqrt{\xcol{x}^4+\xcol{x}}$を$\xcol{x}$によって微分するときは以下のように行なう。 \begin{equation} \underbrace{ \diff \left(\sqrt{\xcol{x}^4+\xcol{x}}\right)}_{\sqrt{\fbox{？}}の微分} =\underbrace{{1\over 2\sqrt{\xcol{x}^4+\xcol{x}}}}_{{1\over 2\sqrt{\fbox{？}}}} \times\underbrace{ \diff (\xcol{x}^4+\xcol{x}) }_{\fbox{？}の微分}={4\xcol{x}^3+1\over 2\sqrt{\xcol{x}^4+\xcol{x}}}\coldx \end{equation}

いくつかの公式

分数関数の微分

　$\ycol{y}={1\over f\kakko{\xcol{x}}}$の微分は、前にやったように、まず$\ycol{y}f\kakko{\xcol{x}}=1$と直してから \begin{equation} \begin{array}{rll} \ycol{y}f\kakko{\xcol{x}}=&1&\kokode{微分}\\[-2mm] \underbrace{\coldy}_{前を微分} f\kakko{\xcol{x}}+\ycol{y}\underbrace{f'\kakko{\xcol{x}}\coldx}_{後を微分} =&0&\kokode{移項}\\ \coldy f\kakko{\xcol{x}}=& -\underbrace{{1\over f\kakko{\xcol{x}}}}_{\ycol{y}}f'\kakko{\xcol{x}}\coldx\\[3mm] {\coldy\over \coldx}=& -{f'\kakko{\xcol{x}}\over \left(f\kakko{\xcol{x}}\right)^2} \end{array} \end{equation} として計算することができる。この式を使うと、$\ycol{y}=\xcol{x}^{-n}={1\over \xcol{x}^n}$の微分は \begin{equation} {\coldy\over \coldx}= -{n\xcol{x}^{n-1}\over (\xcol{x}^n)^2}= {-n\over \xcol{x}^{n+1}}=-n\xcol{x}^{-n-1} \end{equation} のようにしても導ける。

　同様に、$\ycol{y}={g\kakko{\xcol{x}}\over f\kakko{\xcol{x}}}$の微分は以下のように計算すればよい。 \begin{equation} \begin{array}{rll} \ycol{y}f\kakko{\xcol{x}}=&g\kakko{\xcol{x}}&\kokode{微分}\\[-3mm] \coldy f\kakko{\xcol{x}}+\ycol{y}f'\kakko{\xcol{x}}\coldx =&g'\kakko{\xcol{x}}\coldx&\kokode{移項}\\[-3mm] \coldy f\kakko{\xcol{x}}=&g'\kakko{\xcol{x}}\coldx -\ycol{y}f'\kakko{\xcol{x}}\coldx\\[2mm] {\coldy\over \coldx}=&{g'\kakko{\xcol{x}} -\ycol{y}f'\kakko{\xcol{x}}\over f\kakko{\xcol{x}}}&\kokode{\ycol{y}={g\kakko{\xcol{x}}\over f\kakko{\xcol{x}}}を代入して整理}\\ {\coldy\over \coldx}=&{f\kakko{\xcol{x}}g'\kakko{\xcol{x}} -f'\kakko{\xcol{x}}g\kakko{\xcol{x}}\over \left(f\kakko{\xcol{x}}\right)^2} \end{array} \end{equation}

逆関数の微分

　「逆数の微分」ではないので間違えないように（この二つは全く違う）。関数$\ycol{y}=f\kakko{\xcol{x}}$の逆関数$\xcol{x}=f^{-1}\kakko{\ycol{y}}$を微分するとどうなるか、という問題である。導関数は${従属変数の微小変化\coldy\over 独立変数の微小変化\coldx}$という比で計算される。${\coldy\over \coldx}=f'\kakko{\xcol{x}}$なのだから、${\coldx\over \coldy}={1\over f'\kakko{\xcol{x}}}$なのは当たり前である（どちらも、$\coldy=f'\kakko{\xcol{x}}\coldx$を変形すれば得られる）。よって、

---

逆関数の微分

\begin{equation} {\mathrm dx\over \mathrm dy}\kakko{\ycol{y}}={1\over f'\kakko{\xcol{x}}}\biggl|_{\xcol{x}=f^{-1}\kakko{\ycol{y}}}~~~~(f'\kakko{\xcol{x}}を計算したのち、xにf^{-1}\kakko{\ycol{y}}を代入)\label{gyakubibun} \end{equation}

---

という結果になる。「逆関数の微分は関数の微分の逆数」である。

　簡単な例を示しておく。$\ycol{y}=\xcol{x}^n$の逆関数は$\xcol{x}=\ycol{y}^{1\over n}$である。微分してみると、 \begin{equation} \begin{array}{rlc|crl} \ycol{y}=&\xcol{x}^n &~~~~&~~~~&\xcol{x}=&\ycol{y}^{1\over n}\\ \coldy=&n\xcol{x}^{n-1}\coldx &&&\coldx=&{1\over n}\ycol{y}^{{1\over n}-1}\coldy\\[3mm] {\coldy\over \coldx}=&n\xcol{x}^{n-1} &&&{\coldx\over \coldy}=&{1\over n}\ycol{y}^{{1\over n}-1}\\ \end{array} \end{equation} となるが、${1\over n}\ycol{y}^{{1\over n}-1}$の逆数は$n\ycol{y}^{1-{1\over n}}=n(\xcol{x}^n)^{1-{1\over n}}=n\xcol{x}^{n-1}$であり、逆関数の導関数は元の関数の導関数の逆数である。

三角関数の微分

三角関数の微分

準備：三角関数の極限

$\sin \xcol{x}$は$\xcol{x}=0$付近では$\xcol{x}$とほぼ同じ（原点を通り傾き1）であり、$\lim_{\xcol{\Delta x}\to0}{\sin\xcol{\Delta x}\over \xcol{\Delta x}}=1$であった。

$\xcol{x}$が小さいときに$\sin \xcol{x}\simeq \xcol{x}$であることは、電卓による計算で確認した。

　ここで、以下のアプリを使って$\theta,\sin\theta,\tan\theta$が角度が小さいときは「ほぼ一致」することを実感してもらった。

　以下で図解をもう少し詳細に行おう。

　上の図は半径1で中心角$\thetacol{\theta}$の扇型である。扇型の「弧」の部分の長さも$\thetacol{\theta}$となる（これはラジアンという角度の定義）。一方、$\xcol{\sin{\theta}}$というのは図に描かれた線分「$\xcol{\rm PQ}$」に対応する。図には$\tcol{\tan{\theta}}$、すなわち「底辺1の直角三角形の\tcol{高さ}」も示した（この時の「底辺」は図のOPであることに注意）。ここでこの$\thetacol{\theta}$をどんどん小さくしていくところを想像して欲しい。当然、$\xcol{\sin {\theta}}$と$\tcol{\tan{\theta}}$も小さくなる（\極限{$\thetacol{\theta}\to0$}の極限で全て0になるだろう）。

　$\theta$が0付近の小さい角度であるとき、 \begin{equation} \xcol{\sin {\theta}}<\thetacol{\theta}<\tcol{\tan{\theta}} \end{equation} という関係がある。それを示すには、$\sin\thetacol{\theta},\thetacol{\theta},\tan \thetacol{\theta}$の三つは、図に示した三つの経路を伝わって点${\rm P}$から点${\rm Q}$、点${\rm Q'}$、点${\rm Q''}$へと向かう線（真ん中のだけは曲線で、残り２本は直線）の長さであることを使う。

　上の図のように鏡像を持ってきて、${\rm P}$の鏡像にあたる点までの経路を考える（これらの経路の長さは上で考えた長さのそれぞれ2倍となる）。三つの経路の中で、一番「まっすぐ」進んでいる$\xcol{{\rm P}\to {\rm Q}\to{\rm P}の鏡像点}$が一番短く、$\thetacol{{\rm P}\to {\rm Q'}\to{\rm P} の鏡像点}$が中間、もっとも「遠回り」している$\tcol{{\rm P}\to{\rm Q''}\to{\rm P}の鏡像点}$が一番長い。

　以上の説明でなお納得できないという人は、微分の精神である「まず狭い範囲で考える」をここでも活用して考えよう。

　上の図に点線で示したように三角形を$n$階建てのビルだと考え、各々の階での線の長さを見る。各階の高さを小さくすれば（$n$階建ての$n$が無限に大きい極限を考えれば）全ての線はほぼ直線であるから、線の鉛直に対する傾きを見ることで、線の長さが $$ \xcol{\sin\theta の一部}<\thetacol{{\theta}の一部}<\tcol{\tan{\theta}の一部} $$ だとわかる。

　全体の長さは各階での長さの和だから、$\xcol{\sin {\theta}}<\thetacol{\theta}<\tcol{\tan{\theta}}$が得られて、これを正の数である$\thetacol{\theta}$で割ることで、 \begin{equation} {\sin \thetacol{\theta}\over \thetacol{\theta}}< 1 < \underbrace{{\sin \thetacol{\theta}\over \thetacol{\theta}}\times {1\over \cos \thetacol{\theta}}}_{{\tan \thetacol{\theta}\over \thetacol{\theta}}} \end{equation} という式を作ることができて、さらにこの式の右側の部分である$1 < {\sin \thetacol{\theta}\over \thetacol{\theta}}\times {1\over \cos \thetacol{\theta}}$に正の数$\cos\thetacol{\theta}$を掛けると$\cos \thetacol{\theta}<{\sin \thetacol{\theta}\over \thetacol{\theta}}$が得られるから、 \begin{equation} \cos \thetacol{\theta}< {\sin \thetacol{\theta}\over \thetacol{\theta}}< 1 \end{equation} が結論できる。この式を作ってから$\thetacol{\theta}\to0$という極限を取ると、$\cos \thetacol{\theta}\to1$だから、$\cos \thetacol{\theta}$と1の間に挟まれた${\sin \thetacol{\theta}\over \thetacol{\theta}}$も1に近づく$\left(\lim_{\thetacol{\theta}\to0}{\sin \thetacol{\theta}\over \thetacol{\theta}}=1\right)$。これで、

---

$\thetacol{\theta}$が小さい時の$\sin\thetacol{\theta}$の近似式

\begin{equation} \sin \thetacol{\theta}\fallingdotseq \thetacol{\theta}~~~~~より正確には、 \sin \thetacol{\theta}=\thetacol{\theta}+\Odr\kakko{\thetacol{\theta}^3} \end{equation}

---

がわかった残りの部分が$\Odr\kakko{\thetacol{\theta}^2}$ではなく$\Odr\kakko{\thetacol{\theta}^3}$なのは、$\sin$が奇関数（$\sin \kakko{-\thetacol{\theta}}=-\sin \thetacol{\theta}$）だから。$(\thetacol{\theta}^2)$に比例する項はない。。次に$\cos\thetacol{\theta}$の$\thetacol{\theta}$が小さいときの極限を考える。$\cos0=1$、かつ$\cos$は偶関数（$\cos \kakko{-\thetacol{\theta}}=\cos \thetacol{\theta}$）だから$\thetacol{\theta}$の1次の項はない。これからまずは \begin{equation} \cos \thetacol{\theta}=1+a\thetacol{\theta}^2+\Odr\kakko{\thetacol{\theta}^4} \end{equation} として定数$a$を求めてみる。$\sin ^2\thetacol{\theta}+\cos ^2\thetacol{\theta}=1$に代入すると、 \begin{equation} \begin{array}{rll} \bigl( \underbrace{\thetacol{\theta}+\Odr\kakko{{\thetacol{\theta}^3}}}_{\sin \thetacol{\theta}} \bigr)^2 & +\bigl( \underbrace{1+a\thetacol{\theta}^2+\Odr\kakko{{\thetacol{\theta}^4}}}_{\cos \thetacol{\theta}} \bigr)^2 =&1\\[6mm] \thetacol{\theta}^2 + \Odr\kakko{\thetacol{\theta}^4}&+1+2a\thetacol{\theta}^2 + \Odr\kakko{\thetacol{\theta}^4}=&1 \end{array} \end{equation} となるが、右辺は1だから$a=-{1\over 2}$になって左辺の$\thetacol{\theta}^2$の係数が消えなくてはならず、

---

$\thetacol{\theta}$が小さい時の$\cos\thetacol{\theta}$の近似式

\begin{equation} \cos \thetacol{\theta}=1-{1\over 2}\thetacol{\theta}^2+\Odr\kakko{\thetacol{\theta}^4} \end{equation}

---

がわかる。

　上の図のように、$\cos \xcol{x}$と$1-{\xcol{x}^2\over2}$のグラフは$\xcol{x}=0$付近ではそっくりである）。同様に、

---

$\thetacol{\theta}$が小さい時の$\tan\thetacol{\theta}$の近似式

\begin{equation} \tan \thetacol{\theta}=\thetacol{\theta}+\Odr\kakko{\thetacol{\theta}^3} \end{equation}

---

もわかる（$\thetacol{\theta}$が正のとき、$\sin$の$\Odr\kakko{\thetacol{\theta}^3}$は負だが、$\tan$の$\Odr\kakko{\thetacol{\theta}^3}$は正である）。

　これらは今後もよく使う関係式である「覚えよう」とは言わない。何度も使うから覚えてしまうはずだ。「何度も使わない」としたら、勉強が足りない。。これを使って、三角関数の導関数を考えよう。

三角関数の導関数

$\sin$の導関数

---

三角関数の加法定理

\begin{eqnarray} \sin \kakko{A+B}=\sin A\cos B+\cos A\sin B\\ \cos \kakko{A+B}=\cos A\cos B-\sin A\sin B \end{eqnarray}

---

の$\sin$の方を使って \begin{equation} \sin \kakko{\thetacol{\theta}+\coldtheta}=\sin \thetacol{\theta} \underbrace{\cos \coldtheta}_{\to1}+ \cos \thetacol{\theta} \underbrace{\sin \coldtheta}_{\to{\coldtheta}} \end{equation} という式を出す。$\coldtheta$は0に近づけるのだから$\coldtheta$の1次までのオーダーまでしか見ないことにすると$\sin \coldtheta =\coldtheta,\cos\coldtheta=1$であるから、 \begin{equation} \sin \kakko{\thetacol{\theta}+\coldtheta}= \sin \thetacol{\theta}+\underbrace{\cos \thetacol{\theta}}_{微係数}\coldtheta \end{equation} となる。$f\kakko{\xcol{x}+\coldx}=f\kakko{\xcol{x}}+f'\kakko{\xcol{x}}\coldx$と比較することにより、以下がわかる。

---

$\sin$の導関数

\begin{equation} \begin{array}{rl} {\diff }(\sin \thetacol{\theta})=&\cos\thetacol{\theta} \coldtheta,~~~~ \ddtheta(\sin \thetacol{\theta})=\cos\thetacol{\theta} \end{array}\label{ddthetasintheta} \end{equation}

---

右のように、角度$\thetacol{\theta}$を$\coldtheta$だけ変化させた時の、「三角形の高さ」である$\sin\theta$の変化を考える。図に「相似な三角形」として示している「小さい方の三角形の斜辺は曲線だから相似な三角形とは言えないぞ！」と思う人もいるかもしれないが、今$\coldtheta$をどんどん小さくしているので、この曲線は限りなく直線に近い。ように、\coldtheta という長さの弧を斜辺として微小な直角三角形ができていて、この直角三角形の高さにあたる部分が$\coldtheta \cos\thetacol{\theta}$である。$\sin \thetacol{\theta}$の微小変化が$\cos \thetacol{\theta} \coldtheta$と書けるから、微係数は$\cos \thetacol{\theta}$である。

$\cos$の導関数

　こっちはまず図で考えよう。右の図は、$\sin$の導関数の時と同様、斜辺が1の直角三角形の角度を少し変えてみたものである。底辺$\cos \thetacol{\theta}$の変化を見よう。やはり相似な三角形を考えると、$\cos \thetacol{\theta}$の変化量は$\sin \thetacol{\theta} \coldtheta$になりそうである。ただし、この$\cos \thetacol{\theta}$は減っている（変化の方向が負の方向）。ゆえに、以下が導かれる。

---

$\cos$の導関数

\begin{equation} \begin{array}{rl} \diff (\cos \thetacol{\theta})=& -\sin \thetacol{\theta} \coldtheta,~~~ \ddtheta(\cos \thetacol{\theta})= -\sin \thetacol{\theta} \end{array} \end{equation}

---

　$\sin $と同じ手順で数式で考えることもできる。三角関数の加法定理を使って、 \begin{equation} \begin{array}{rll} \cos \kakko{\thetacol{\theta}+\coldtheta} =&\cos \thetacol{\theta} \underbrace{\cos \coldtheta}_{1} - \sin \thetacol{\theta} \underbrace{\sin \coldtheta}_{\coldtheta}=\cos \thetacol{\theta} \underbrace{- \sin \thetacol{\theta}}_{微係数} \coldtheta \end{array} \end{equation} を得るから、$\ddtheta(\cos \thetacol{\theta})= -\sin \thetacol{\theta}$となる。

　この（一方にマイナス符号がつく意味）は、次の図のように、微分という操作が図上ではちょうど「90度$\left({\pi\over 2}\right)$の回転」に対応しているからだと思ってもよい。

　${\pi\over 2}$の回転はのように、$\xcol{x}$座標を$\ycol{y}$座標に、$\ycol{y}$座標を（符号を変えて）$\xcol{x}$座標にすることで得られる。式で書くなら$(x,y)\to(-y,x)$であるが、これが微分$(\cos \theta,\sin \theta)\to(-\sin \theta,\cos \theta)$と同じ計算になっている。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。